Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.
| Вид материала | Книга |
Содержание§ 6.6. Дополнительные измерители эффективности § 6.7. Моделирование инвестиционного процесса K5 — закупка и поставка оборудования; K |
- Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
- Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
- Планирование производственных запасов и определение потребности предприятия, 53.58kb.
- Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
- Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
- Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
- Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
- И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.
§ 6.6. Дополнительные измерители эффективности
В западной практике применяется ряд дополнительных показателей эффективности производственных инвестиций, которые базируются на наращении процентов. К ним, в частности, относится показатель, который в литературе называют средним приростом доходов (growth rate of return)31.
Предполагается, что все доходы от проекта реинвестируются по ожидаемой ставке j. Суммарный доход на некоторый момент времени Т составляет вместе с начисленными на поступления процентами сумму B. Поскольку инвестиции осуществлены в размере K, то логично записать следующее соотношение между инвестициями и предполагаемым суммарным доходом:
K(1 + GR)T = В, (6.22)
где GR — средний темп прироста капитала. Откуда
(6.23)Если рассматривается непрерывный поток доходов, то имеем KеqТ = B и, следовательно,
(6.24)где q — непрерывный темп прироста капитала.
Как следует из формул (6.23) и (6.24), искомые величины являются расчетными уровнями процентных ставок для роста капитала от K до B.
Известный интерес представляет взаимосвязь этих ставок и чистого приведенного дохода. По определению
N = B(1 + j)-T -К.
Таким образом,
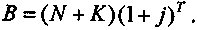(6.25)Подставив (6.25) в (6.22), получим
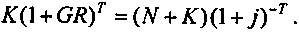
Из последней записи следует
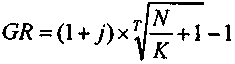(6.26)и
ПРИМЕР 10
Обратимся к первым двум потокам платежей табл. 6.2.
| А: | -100 | -150 | 50 | 150 | 200 | 200 | 50 |
| Б: | -200 | -50 | 50 | 100 | 100 | 200 | 200 |
Положим, что все платежи производятся в конце года. Тогда при условии, что j = 10%, получим KА = 260 и KБ = 270. По формуле (6.26) получим
GRА = 1,15 х
- 1 = 0,321;GRБ = 1,15 х
- 1 = 0,262.В свою очередь, для непрерывного потока доходов найдем
,где
— непрерывная ставка реинвестирования дохода.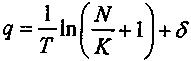
и, наконец,
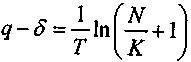(6.27)Из (6.26) следует, что показатель GR можно рассматривать как меру, адекватную чистому приведенному доходу в том смысле, что при положительной величине N темп прироста капитала больше ставки реинвестирования j. В формулах (6.26) и (6.27) рассматриваемый темп функционально связан с отношением N/K. Отсюда следует, что ранжирование инвестиционных проектов по величине GR приведет к аналогичным результатам, что и ранжирование по N.
Иногда весь период отдачи делят на два подпериода с разными условиями начисления процентов. В первом — до конца срока окупаемости — начисления производятся по принятому нормативу доходности, во втором — к "новым деньгам" применяется ставка реинвестирования32. В ряде случаев обходятся без срока окупаемости, разделяя весь предполагаемый срок на две равные половины. Как видим, подходы к решению проблемы измерения эффективности здесь весьма произвольные.
§ 6.7. Моделирование инвестиционного процесса
Параметры эффективности можно получить и для сложных инвестиционных схем. В этих случаях уместно прибегнуть к разработке специальных экономико-математических моделей, состоящих из математических выражений, описывающих как процесс формирования потоков платежей, так и соотношений, позволяющих рассчитать искомые величины. Основное преимущество использования модели, как известно, заключается в одновременном учете в ней всех необходимых требований, условий и предположений. Имеется определенная свобода в пересмотре этих установок в ходе работы с моделью, а сами результаты (показатели) оказываются непротиворечивыми. Модель позволяет получить варианты поведения исследуемого явления (в нашем случае — инвестиционного процесса) для разнообразных сочетаний исходных условий и принятых предположений, например состояния денежно-кредитного рынка, уровня инфляции, спроса на выпускаемую продукцию и т. д. Особенность модели, разрабатываемой для инвестиций в производство, составляет то, что в ней базовым является блок, в котором формируются затраты и отдачи от инвестиций для каждого временного интервала со специфическим их распределением в его пределах. Во втором блоке модели определяются искомые показатели эффективности.
Очевидно, нет смысла строить детальную модель, если имеется в виду только получение оценки для одного варианта условий. Преимущества модельного подхода в этом случае не используются. Модель дает возможность осуществить так называемый анализ отзывчивости, или чувствительности (sensitive analysis), о котором речь пойдет в следующем параграфе. Здесь только кратко заметим, что названный анализ заключается в выявлении наиболее важных (ключевых) входных параметров модели и получении системы оценок эффективности инвестиций для широкого диапазона значений этих параметров. Таким образом, лицу, принимающему решение, предоставляется не единственная, точечная оценка, а развернутая картина (в виде таблиц и графиков) значений эффективности для разнообразных возможных и ожидаемых ситуаций.
Первый шаг при разработке базового блока модели заключается в определении структуры потока платежей во времени (разбиение его на этапы). Причем и затраты и доходы в модели должны быть увязаны как с внешними (экзогенными) условиями, так и с производственными параметрами, например в связи с ожидаемой динамикой цен на производимую продукцию (внешние условия) и возможными изменениями объемов производства и уровней текущих производственных затрат. Данные о затратах и доходах в зависимости от конкретных условий могут быть постоянными и переменными, дискретными и непрерывными. Например, данные о затратах на изыскательские работы и проектирование можно рассматривать как постоянные в некотором ограниченном интервале времени, строительство и закупку оборудования — как переменные, а эксплуатационные расходы — как постоянные затраты и т. д. Доходы часто представляют собой непрерывный поток поступлений.
Модель разрабатывается на основе трех видов данных — уровней или объемных характеристик (выпуск продукции, затраты на строительство и т. д.), временных параметров (моменты начала или окончания отдельных этапов, сроки), "нормативных" показателей (удельные расходы, процентные и налоговые ставки, ожидаемые цены и др.). Часть этих данных заложена в техническом проекте, другая получается из разных источников, включая специальные исследования и экспертные оценки.
Приведем иллюстрацию. Пусть для большей определенности речь пойдет о создании предприятия по добыче каких-либо полезных ископаемых. Последовательность основных этапов во времени показана на рис. 6.12.
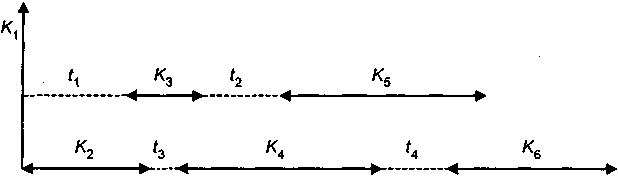
Рис. 6.12
Обозначения:
Kj — величина затрат на этапе j;
nj — протяженность этого этапа;
tk — расстояние от начального момента или между этапами (периоды отдачи на рисунке не показаны);
K1 — приобретение участка земли (разовые затраты);
K2 — изыскательские работы;
K3 — проектирование;
K4 — строительство;
K5 — закупка и поставка оборудования;
K6 — монтаж и наладка оборудования.
Для простоты положим, что в пределах каждого этапа затраты распределены равномерно. Если это не так, то на протяжении соответствующих этапов можно выделить подпериоды с относительно равномерными инвестиционными расходами.
Общий срок создания предприятия составит:
n = п2 + t3 + n4 + t4 + n6.
Определим современную стоимость инвестиционных расходов относительно начального момента времени. При расчете этой величины используем следующий подход: если протяженность этапа равна году или менее, то вся сумма расходов относится к середине периода, если этап занимает несколько лет, то поток платежей рассматривается как постоянная рента. Для каждого из перечисленных этапов находим следующие искомые значения современных стоимостей и их сумму:
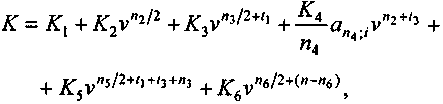
где v — дисконтный множитель по ставке i.
Что касается периода отдачи, то положим, что он состоит из двух интервалов — в первом, сроком n7 лет, ожидается годовой доход (за вычетом текущих затрат) в размере R7, во втором, протяженностью n8 , доход падает (месторождение истощается) примерно на 100h% в год. Для простоты годовую сумму дохода можно без большой потери точности отнести к середине года. Современная стоимость поступлений составит:
Рассмотренная модель может быть детализирована во многих отношениях, и прежде всего путем раскрытия механизма формирования переменных Kj и Rj . Например, последнюю величину можно представить в модели как
,где Qkj — объем продукции вида k, выпущенной в периоде j;
pkj — чистый доход от реализации единицы этой продукции.
В свою очередь, можно ввести в модель расчет показателя чистого дохода и таким образом увязать ее с рядом внешних условий: ценами на продукцию, уровнем заработной платы, стоимостью сырья и т. д. Чем полнее будут охвачены факторы, формирующие затраты и чистый доход, тем больше возможностей для анализа и сокращения риска. Более того, если имеются варианты использования разного сырья и (или) технологий, а также какие-либо альтернативы в строительстве, то это также должно быть отражено в модели.
Приведенная выше модель является дискретной. Однако ее можно трансформировать и представить некоторые составляющие в виде непрерывных величин. В этом случае существенно увеличивается гибкость при описании соответствующих сторон инвестиционного процесса. Например, достаточно просто учесть влияние систематического изменения цен и другие непрерывно действующие факторы. Вернемся к нашей модели. Пусть ожидается, что цены на продукцию предприятия в первом периоде будут расти со средним годовым непрерывным темпом прироста
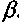. Тогда суммарный доход в первом году этого периода составит
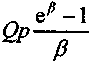,а за все n7 лет
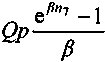.Переменные Q и р означают годовой выпуск и цену на начало года. Современная стоимость дохода, определенная на начальный момент разработки проекта, равна
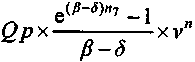,где е — основание натуральных логарифмов;
— непрерывная ставка, принятая для дисконтирования, ее соотношение с дискретной ставкой; 
= ln(1 + i) .