Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.
| Вид материала | Книга |
- Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
- Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
- Планирование производственных запасов и определение потребности предприятия, 53.58kb.
- Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
- Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
- Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
- Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
- И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.
§5.4. Математическое приложение
а. Некоторые стандартные функции
ln еx = х;
(еx)' = еx ; (аx)' = ax ln а;
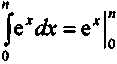= еn - 1;
б. Производная и интеграл функции у = еat.
Для расчета современной стоимости и наращенной суммы непрерывного потока платежей необходимо определить производную и интеграл функции у = еat, где а — постоянная величина, t — продолжительность потока платежей.
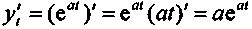. (1)Соответственно при наращении и дисконтировании по непрерывной ставке
имеем:
.В свою очередь, первообразная для функции еat имеет вид eat/a, так как в силу (1) (еat/а)' = еat. Отсюда
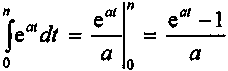. (2)При использовании непрерывной ставки
получим следующие коэффициенты приведения и наращения постоянного потока платежей: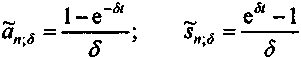
.в. Определение интеграла
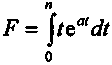. Интегрируем функцию F по частям.
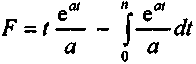.Воспользуемся формулой (2), после чего
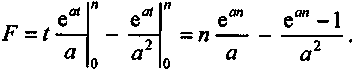
Если речь идет о непрерывном дисконтировании по ставке
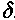, то а = -
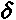и, следовательно,
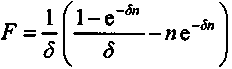. (3)г. Определение современной стоимости "треугольного" потока платежей
На основе рис. 5.2 получим
(4)Общий принцип определения современной стоимости потока платежей:
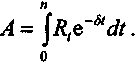
Применим соотношение (4), после чего
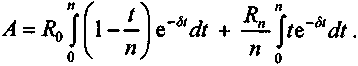
После небольших преобразований получим
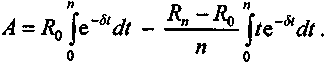
Воспользовавшись (2) и (3), окончательно имеем:
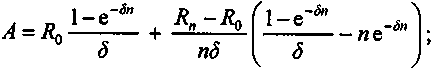
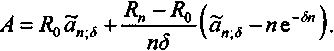(5)д. Доказательство формулы (5.14) Исходные условия:
R0 = 0; М =
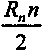; Rn =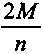
Теперь на основе (5) получим
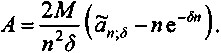
ГЛАВА 6 ИЗМЕРИТЕЛИ ЭФФЕКТИВНОСТИ КАПИТАЛОВЛОЖЕНИЙ: ВНУТРЕННЯЯ НОРМА ДОХОДНОСТИ И ДРУГИЕ ХАРАКТЕРИСТИКИ
Великая научная идея редко внедряется путем
постепенного убеждения своих противников...
В действительности депо происходит так,
что оппоненты постепенно вымирают,
а растущее поколение с самого начала
осваивается с новой идеей...
М. Планк
§ 6.1. Внутренняя норма доходности
Не менее важным показателем для финансового анализа производственных инвестиций наряду с чистым приведенным доходом является внутренняя норма доходности. Под этим критерием понимают такую расчетную ставку приведения, при которой капитализация получаемого дохода дает сумму, равную инвестициям, и, следовательно, капиталовложения окупаются, но не приносят прибыль. Иначе говоря, при начислении на сумму инвестиций процентов по ставке, равной внутренней норме доходности J, обеспечивается получение распределенного во времени дохода, эквивалентного инвестициям. В терминах метода барьерных точек J является управляющей переменной, а "конкурирующими" функциями будут современные стоимости капитальных вложений и отдачи от них.
Чем выше эта норма, тем больше эффективность инвестиций. Данный параметр может быть как положительной, так и отрицательной величиной. Последнее означает, что инвестиции не окупаются. Величина этой ставки полностью определяется "внутренними" условиями, характеризующими инвестиционный проект. Никакие предположения об использовании чистого дохода за пределами проекта не рассматриваются.
Пусть i — приемлемый для инвестора уровень ставки процента (выше она была названа минимально привлекательной ставкой доходности или нормативом доходности). Очевидно, что разность ставок (J - i) характеризует эффективность инвестиционной (предпринимательской) деятельности. С чисто финансовых позиций инвестиции имеют смысл только тогда, когда J > i. При J < i нет оснований для осуществления инвестиций, так как доходность ниже принятого норматива; если же под i понимается стоимость заемных средств, то инвестиции просто убыточны.
Расчет внутренней нормы доходности часто применяют в качестве первого шага анализа инвестиций (см. § 5.1). Для дальнейшего анализа в западной практике отбираются только те проекты, которые обеспечивают некоторый приемлемый для данной компании уровень доходности. Последний зависит от многих объективных и субъективных обстоятельств и охватывает весьма большой диапазон возможных значений даже для однородных видов предприятий. Так, при обследовании нефтяных компаний США (см. гл. 5) было получено следующее распределение величины этого показателя28 (табл. 6.1).
Таблица 6.1
| Приемлемый уровень доходности (%) | Доля в общем числе обследованных фирм (%) |
| Менее 5 | 4 |
| От 5 до 10 | 8 |
| Свыше 10 до 25 | 6 |
| Свыше 25 до 50 | 19 |
| Свыше 50 до 80 | 26 |
| Свыше 80 | 23 |
| Не ответили | 14 |
Методы расчетов. В общем случае, когда инвестиции и доходы задаются в виде потока платежей, искомая ставка29 определяется на основе решения уравнения (6.1) относительно v
(6.1)где v — в данном случае представляет собой дисконтный множитель по искомой ставке J;
t — время от начала реализации проекта;
Rt — член потока платежей (вложения и чистые доходы).
Инвестиции имеют в этом равенстве отрицательный знак, доходы — положительный. Если все члены потока имеют один знак, то, естественно, искомую ставку получить нельзя. Положительное значение J имеем, когда сумма дисконтированных доходов больше размера инвестиций, отрицательное — в противоположном случае.
Чистый приведенный доход, при условии что дисконтирование членов потока производится по ставке J, по определению равен нулю (см. рис 5.4). На рисунке кривая пересекает ось i только один раз — в точке J. Это типовой случай. Однако при специфическом распределении членов потока во времени последовательные члены потока платежей могут изменять свой знак несколько раз (например, если ожидаются в будущем крупные затраты на модернизацию процесса производства). В этих случаях кривая пересекает эту ось несколько раз (см. рис. 5.5). Соответственно можно получить несколько значений искомой ставки (несколько корней многочлена), удовлетворяющих (6.1).
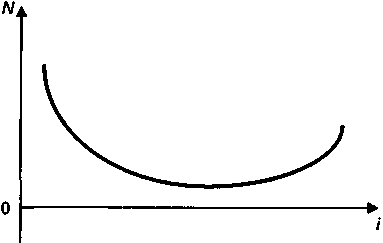
Рис. 6.1
В редких, но теоретически возможных случаях чистый приведенный доход оказывается положительной величиной при любом значении ставки i (см. рис. 6.1). Величина J здесь просто отсутствует. Если имеется множественность значений J или оно отсутствует, то при сравнении нескольких инвестиционных проектов следует воспользоваться другими измерителями эффективности.
Расчет искомой ставки осуществляется различными методами, дающими разные по точности ответы. Различаются они и по трудоемкости. В западной учебной литературе часто ограничиваются методом последовательного подбора значения ставки до выполнения условия N = 0. Действительно, при наличии опыта и сравнительно коротком потоке платежей такой подход довольно быстро дает удовлетворительные результаты.
ПРИМЕР 1
Рассчитаем J для данных примера 1 (вариант А) (см. § 5.2). Напишем уравнение, в котором для сокращения записи примем 1 + J = r . Исходная функция, определяющая чистый приведенный доход,
N(r) = -100r -1 - 150r -2 + 50r -3 + 150r -4 + 200r -5 + 200r -6 = 0 .
Решение заключается в определении корня шестой степени. Применим метод последовательного подбора. Возьмем в качестве исходной ставку, равную, допустим, 15%. Найдем величину чистого приведенного дохода по этой ставке: N(1,15) = 104,2, т.е. заметно отличается от нуля. Принятое значение ставки мало.
Изменяя величину ставки в нужном направлении, приближаемся к условию N(r) = 0. Повысим r до уровня, допустим, 1,25. Имеем N(1,25) = 29,0. Ноль в значении функции опять не достигнут.
Далее находим N(1,3) = 4,9 . Можно окончить расчет и удовлетвориться достигнутой точностью или продолжить его и еще раз увеличить ставку, например до 31%. В этом случае N(1,31) = 0,8 . Увеличивать точность расчета далее, вероятно, не имеет смысла.
Можно применить и линейную интерполяцию, если из прошлого опыта известен примерный диапазон значений для J. На рис. 6.2 приведен график, на основе которого легко получить интерполяционную формулу следующего вида:
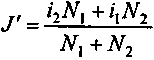(6.2)где i1, i2 — границы диапазона для ставки J;
N1, N2 — величины чистого приведенного дохода при дисконтировании по ставкам i1, i2.
На рис. 6.2 точное значение внутренней нормы доходности равно J. Расчетная ее оценка составляет J'. Очевидно, что чем уже интервал ставок i1 - i2, тем меньше погрешность этой оценки.
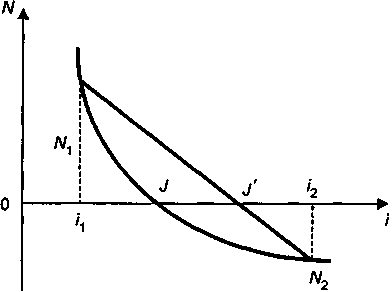
Рис. 6.2
ПРИМЕР 2
Ожидается, что внутренняя норма доходности для потока платежей примера 1 находится в интервале 25 — 35%.
Находим N1 = 29,0; N2 = 13,25 (знак минус не принимаем во внимание). В итоге
J' =
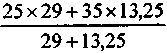= 28,14%. Проверка: N = 13,9.Оценка размера внутренней нормы доходности оказалась заниженной. Уточним ее. Для этого несколько сузим интервал значений ставки. Воспользуемся уже полученными значениями N: для ставки 28,14% N = 13,9, а для ставки 35% N =13,25.
По интерполяционной формуле получим J' = 31,59% . Проверка: N = -1,59, т. е. расчетное значение близко к нулю. Точность оценки заметно повысилась.
Более "серьезные" методы определения J основываются на различных итерационных процедурах, к которым, в частности, относятся метод Ньютона—Рафсона и метод секущей30 или какие-либо численные процедуры, например метод поразрядного приближения.
В случае, когда инвестиции "мгновенны", а поток доходов может быть представлен в виде постоянной ренты, задача упрощается и сводится к определению ставки J на основе знакомого нам равенства:
K = Ran;J . (6.3)
Из этой формулы следует
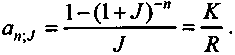(6.4)Таким образом, задача заключается в расчете искомой ставки по заданному коэффициенту приведения постоянной ренты (см. гл. 1).
ПРИМЕР 3
Инвестиции к началу срока отдачи от них составили 4 млрд. руб. Доход ожидается на уровне 0,7 млрд. руб. в год, поступления в течение 10 лет.
Если полагать, что поступления происходят равномерно в пределах года (соответственно их можно приурочить к серединам соответствующих лет), то коэффициент приведения ренты, необходимый для определения искомой нормы, можно записать следующим образом:
а10;J(1 + J)0,5 =
= 5,7143,что соответствует J = 13,1%.
В свою очередь, если поток доходов непрерывен и постоянен, то непрерывная внутренняя норма доходности D находится на основе коэффициента приведения непрерывной ренты:
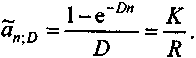(6.5)Влияние факторов. На величину внутренней нормы доходности влияют те же факторы, что и на чистый приведенный доход, а именно размеры инвестиционных расходов и доходов и специфика их распределений во времени. Однако влияние здесь обратное: все, что увеличивает N, сокращает значение J. В частном случае, когда инвестиции мгновенны, а доходы можно представить в виде постоянной ренты, зависимость нормы доходности от факторов обретает конкретный вид (рис 6.3). В том случае, когда K/R = п , внутренняя норма доходности равна нулю (точка а на рис. 6.3). Соотношение инвестиций и годового дохода оказывается эффективным только тогда, когда оно меньше величины b.
Рис. 6.3
Зависимость внутренней нормы доходности от продолжительности поступлений дохода очевидна: чем она больше, тем выше эта норма при всех прочих равных условиях. Однако ее прирост затухает по мере увеличения п.
При использовании внутренней нормы доходности в качестве ориентира для выбора и принятии инвестиционного решения следует иметь в виду, что
- данный параметр эффективности не учитывает масштабов проекта;
- существует возможность (правда, редкая) в некоторых ситуациях получить неоднозначные оценки эффективности, а иногда они вовсе отсутствуют;
- при отсутствии опыта расчета или соответствующих программ получение значения критерия может быть связано с некоторыми затруднениями.
Здесь уместно привести два дополнительных замечания, затрагивающих как внутреннюю норму доходности, так и чистый приведенный доход. Так, если инвестиционный проект охватывает ряд самостоятельных объектов, каждый из которых характеризуется определенными капитальными затратами и отдачами от них, то для этих составных частей можно определить частные показатели чистого приведенного дохода. Чистый приведенный доход проекта в целом равен сумме частных показателей. Этого нельзя сказать о внутренней норме доходности.
Потребность в применении того или другого показателя эффективности связана с различием в их содержании. Если речь идет о максимизации массы дохода, то резонно выбор проекта основывать на чистом приведенном доходе (такой выбор, разумеется, не обеспечивает наиболее эффективного использования затраченных средств). При стремлении максимизировать относительную отдачу ориентируются на внутреннюю норму доходности.