Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.

Вид материала

Книга

Содержание § 4.3. Минимизация дисперсии дохода А — вектор, характеризующий (п

Подобный материал:

• Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
• Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
• Планирование производственных запасов и определение потребности предприятия, 53.58kb.
• Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
• Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
• Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
• Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
• Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
• Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
• И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.

§ 4.3. Минимизация дисперсии дохода

Приведенные выше выражения для дисперсии суммарного дохода позволяют рассмотреть проблему диверсификации инвестиций и риска еще в одном аспекте, а именно определить структуру портфеля, которая минимизирует дисперсию и, следовательно, риск. Для нахождения минимума дисперсии вернемся к определяющим ее формулам. Если предположить, что нет статистической зависимости между доходами от отдельных видов инвестиций, то найти оптимальную в указанном смысле структуру портфеля не так уж и сложно. Положим, что портфель состоит из двух видов бумаг — X и Y. Их доли в портфеле составляют а_х и 1 - а_х, а дисперсии — D_x и D_y. Общая дисперсия определяется по формуле (4.5). Поскольку эта функция является непрерывной, то применим стандартный метод определения экстремума. Находим, что минимальное значение дисперсии суммы имеет место тогда, когда

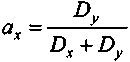, (4.12)

a_y = 1 - a_x.

Формулу (4.12) обычно приводят в аналитической финансовой литературе. Однако для того чтобы ею можно было воспользоваться, необходимо иметь значения дисперсий. По-видимому, при расчетах на перспективу удобнее оценить или задать экспертным путем не сами дисперсии, а их отношение

D_x/y = D_x/D_y. (4.13)

Разделим теперь числитель и знаменатель (4.12) на D_y, получим

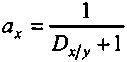. (4.14)

При наличии корреляции между показателями доходов обратимся к (4.6). Минимум этой функции имеет место в случае, когда

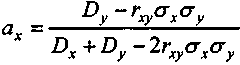, (4.15)

или, с помощью отношения дисперсий (4.13), получим

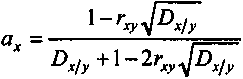. (4.16)

Как видно из приведенных формул, расчетная величина доли одной из бумаг может в некоторых условиях оказаться отрицательной. Из этого следует, что этот вид бумаги не должен включаться в портфель.


ПРИМЕР 2

Вернемся к данным примера 1 и определим структуру портфеля с минимальной дисперсией. Напомним, что = 0,8; 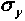= 1,1.

При полной положительной корреляции расчетные значения доли первой бумаги составят по формуле (4.15)

.

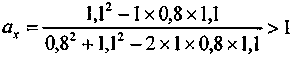Соответственно а_у < 0 . Следовательно, минимальная дисперсия имеет место в случае, когда портфель состоит из одной бумаги вида X. Средний доход от портфеля равен 2.

При полной отрицательной корреляции находим

а_x = 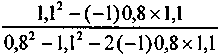= 0,579;

a_y = 1 - 0,579 = 0,421.

Дисперсия в этом случае равна нулю (рис. 4.4), а средний доход составит 2,421.

При отсутствии корреляции получим по формуле (4.12)

а_х = 0,654; а_у = 1 - 0,654 = 0,346.

Дисперсия дохода при такой структуре портфеля равна 0,418, а средний доход — 2,346.

Пусть теперь портфель состоит из трех видов бумаг — X, Y, Z. Их доли а_х, а_у и a_z = 1 - (a_x + a_y). Дисперсия дохода от портфеля при условии независимости доходов от отдельных видов бумаг составит:



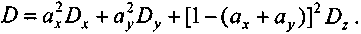
Минимум дисперсии достигается, если структура портфеля определяется следующим образом:





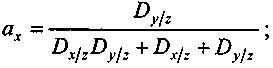
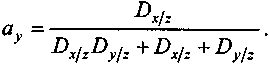
Не будем останавливаться на ситуации, когда доходы трех видов бумаг статистически зависимы. Перейдем к общей постановке задачи и определим структуру портфеля с n составляющими. Положим, что доходы статистически независимы. Опустим доказательства (см. § 4.4) и приведем результат в матричном виде:

A = D^-1e, (4-17)

где e — единичный вектор, характеризующий структуру портфеля.



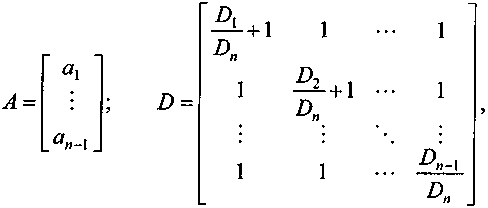
где А — вектор, характеризующий (п - 1) элементов структуры портфеля.

Матрица D имеет размерность (n - 1) х (п - 1) .


ПРИМЕР 3

Эксперты оценили следующие отношения дисперсий для портфеля, состоящего из четырех видов бумаг: D_l/4 = 1,5; D_2/4 = 2 ; D_3//₄ = 1. По формуле (4.17) получим

, откуда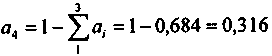

.


Заметим, что структуру портфеля, минимизирующую дисперсию дохода с и составляющими при наличии корреляции, определить так же просто, как это было сделано выше, нельзя. Однако решение существует, хотя его получение — достаточно хлопотное дело. Даже в матричном виде результат весьма громоздок, в силу чего эта задача здесь не обсуждается.

Анализ диверсификации представляет собой первый этап в исследовании портфеля инвестиций. Следующим этапом является максимизация дохода. Эта проблема также связана с измерением риска и требует обстоятельного специального обсуждения, выходящего за рамки настоящей работы. Поэтому ограничимся лишь замечанием о том, что предлагаемый для ее решения метод Марковица²² в теоретическом плане не вызывает возражений. Что касается его практического применения, то здесь, на наш взгляд, скрыты серьезные "подводные камни". Достаточно подробное и простое изложение теории Марковица читатель может найти в книге Ю. Ф. Касимова "Основы теории оптимального портфеля ценных бумаг" (М.: Филинъ, 1998).