Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.
| Вид материала | Книга |
Содержание§ 3.4. Положение барьерных точек при неопределенности в исходных данных § 3.5. Барьерные точки объемов производства, финансовый подход к их определению |
- Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
- Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
- Планирование производственных запасов и определение потребности предприятия, 53.58kb.
- Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
- Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
- Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
- Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
- И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.
§ 3.4. Положение барьерных точек при неопределенности в исходных данных
Барьерное значение выпуска продукции определялось выше для линейной и нелинейной моделей при условии, что все исходные данные установлены однозначно. В этой ситуации получают только одно расчетное значение выпуска. В действительности все не так просто. Так, цену продукции, вероятно, можно с большей надежностью определить для будущего лишь в виде некоторого интервала
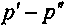 . Обратившись к линейной модели, получим интервал значений барьерного выпуска продукции
. Обратившись к линейной модели, получим интервал значений барьерного выпуска продукции 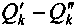 (рис. 3.10).
(рис. 3.10).Аналогичное можно сказать и об остальных параметрах в формуле (3.3). Таким образом, при условии, что неоднозначными являются постоянные или переменные затраты, получим диапазоны барьерных показателей выпуска для линейной модели (рис. 3.11 и рис. 3.12).
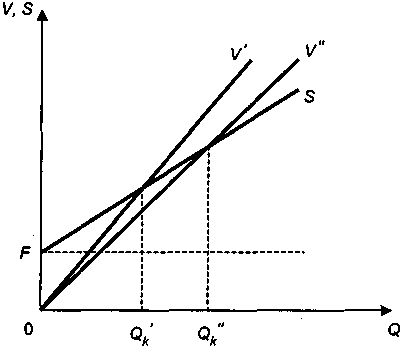
Рис. 3.10
На рис. 3.13 иллюстрируется совместное влияние на положение барьерного выпуска продукции неопределенности в цене продукции и переменных затратах. На этом же рисунке показана зависимость размера прибыли от выпуска продукции для двух крайних сочетаний значений параметров p и с. В свою очередь, неоднозначность в ожидаемой цене продукта и постоянных затратах приводит к результату, который показан на рис. 3.14.
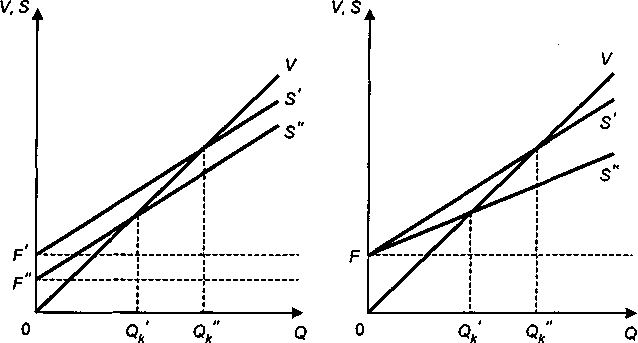
Рис. 3.11 Рис. 3.12
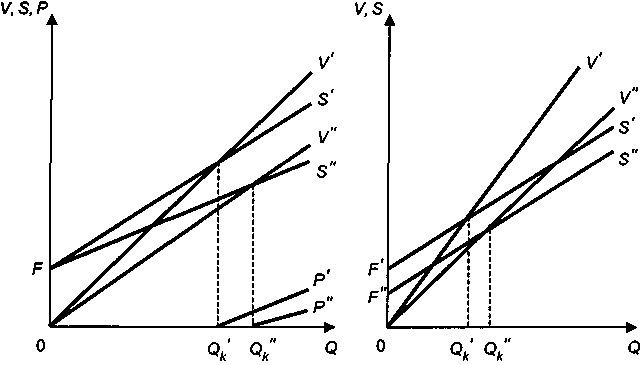
Рис. 3.13 Рис. 3.14
На рис. 3.15 показана ситуация, при которой интервалами заданы значения всех трех параметров — четыре критические точки: а, b, с, d, причем точка а соответствует минимальным затратам и максимальной цене, точка b — максимальным затратам и цене, точка с — максимальным затратам и минимальной цене, точка d — минимальным затратам и цене. В зависимости от выдвинутых условий можно получить ряд диапазонов для барьерной точки: а — b, а — с и т. д. Определение диапазонов значений управляющей переменной является частным случаем анализа, о котором речь пойдет в гл. 6.
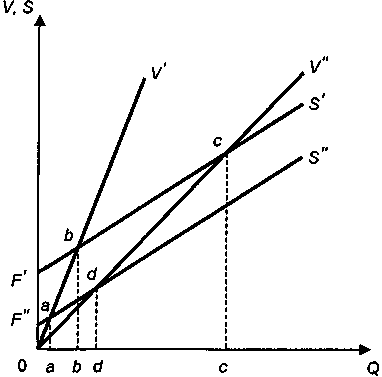
Рис. 3.15
Что касается способов определения интервалов для значений параметров, то в большинстве случаев вполне оправданно экспертное их оценивание (см. гл. 8).
Расчет интервалов для барьерных значений управляющих переменных дает более полное представление о реально ожидаемых результатах производственной деятельности. Рассмотренный метод определения таких интервалов представляет частный случай анализа чувствительности, о котором речь пойдет в гл. 6.
§ 3.5. Барьерные точки объемов производства, финансовый подход к их определению
Постановку задачи по определению барьерного объема выпуска продукции можно расширить, учитывая дополнительные условия. Представим себе, что разрабатывается проект по производству некоторого нового вида продукции. Выпуск продукции намечен в течение n лет в равных объемах по годам. Что касается затрат, то сохраняется их деление на постоянные (не связанные с объемами производства) и переменные (пропорциональные выпуску продукции). Таким образом, и текущие затраты, и поступления от реализации продукции можно представить в виде потоков платежей. Здесь возможны два конкурирующих подхода к решению. В первом, который условно назовем бухгалтерским, инвестиции не принимаются во внимание непосредственно — они учитываются через амортизационные отчисления. Последние включают в текущие затраты. Во втором, финансовом подходе инвестиции играют ключевую роль: они выступают в качестве самостоятельного фактора, в то время как амортизация не учитывается в текущих расходах.
Как видим, оба метода избегают двойного счета инвестиционных затрат.
Указанные методы применяются на практике и, естественно, дают разные результаты. Начнем с бухгалтерского, согласно которому необходимо определить тот минимальный объем выпуска, при котором затраты окупятся, но не принесут прибыли. Иначе говоря, метод предполагает ориентацию на прибыль.
Найдем размер прибыли в зависимости от объема выпуска продукции для одного временного интервала:
P = pQ - (cQ + f + d),
где p и с имеют тот же смысл, что и выше (см. §3.1);
f — постоянные расходы за год;
d — сумма амортизационных списаний за тот же период.
Пусть сумма амортизации определена линейным способом, т. е. d = const.
Если принять во внимание тот факт, что выпуск продукции (поступления дохода) и затраты представляют собой потоки платежей, то "конкурирующие" функции определяются как современные стоимости соответствующих потоков, а именно: PV(pQ) и PV(f + d + cQ), где PV— оператор определения современной стоимости соответствующего потока. Графическая иллюстрация положения барьерной точки выпуска представлена на рис. 3.16.
Конкретизируем сказанное и найдем барьерную точку выпуска для условия, согласно которому выпуск и реализация продукции равномерно распределены в пределах года. В связи с этим без заметной потери точности в расчетах отнесем эти величины к серединам соответствующих лет.
Барьерный объем выпуска продукции составит (см. § 2.6):
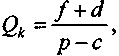 (3.21)
(3.21)что, по существу, совпадает с формулой (3.3). Отличие от последней состоит только в выделении в числителе в качестве самостоятельного слагаемого суммы амортизационных расходов.
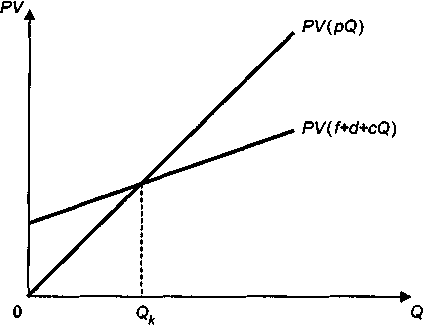
Рис. 3.16
Предположим теперь, что все участвующие в расчете удельные характеристики изменяются во времени, т. е. вместо p, c, f, d имеем pt, ct, ft, dt. Переменные параметры, несомненно, более адекватны реальности. Например, затраты на производство растут в связи с увеличением расходов на ремонт по мере износа оборудования, в то же время постоянные затраты могут уменьшаться. В ряде случаев есть основание задаться некоторой закономерностью изменения цен продукции во времени и т. д. Равенство современных стоимостей "конкурирующих" функций в этом случае имеет вид
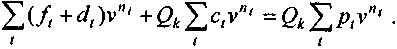
Отсюда
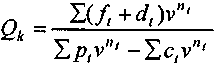 . (3.22)
. (3.22)ПРИМЕР 8
В таблице приведены исходные данные для расчета барьерного выпуска на основе потоков платежей. Все параметры, кроме сумм амортизации, здесь переменные величины и рассчитаны на 1000 единиц выпуска продукции.
| t | p | с | f | d |
| 1 | 50 | 28 | 20 | 30 |
| 2 | 50 | 28 | 20 | 30 |
| 3 | 46 | 30 | 16 | 30 |
| 4 | 46 | 30 | 16 | 30 |
| 5 | 42 | 31 | 12 | 30 |
Для дисконтирования применим процентную ставку 15%. Необходимые для расчета по формуле (3.22) данные приведены в следующей таблице.
| t | vn | f + d | (f+d)vn | pvn | cvn |
| 1 | 0,93250 | 50 | 46,62500 | 46,62500 | 26,11000 |
| 2 | 0,81087 | 50 | 40,54350 | 40,54350 | 22,70436 |
| 3 | 0,70511 | 48 | 32,43506 | 33,84528 | 21,15330 |
| 4 | 0,61314 | 45 | 28,20444 | 27,59130 | 18,39420 |
| 5 | 0,53316 | 42 | 22,39284 | 22,39283 | 16,52804 |
| Итого | | — | 170,20008 | 170,99791 | 104,88990 |
| Qk = 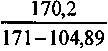 = 2,57. = 2,57. | |||||
Перейдем к финансовому методу, который в отличие от бухгалтерского учитывает размер капитальных вложений, непосредственно осуществленных для реализации проекта, и поток чистых поступлений (без учета амортизационных отчислений). В частном случае, когда удельные характеристики постоянны, имеем следующую последовательность платежей:
-K, (p - c)Q - f, (p - c) Q - f, ...
где K — размер инвестиций.
Современная стоимость такого потока представляет собой чистый приведенный доход (показатель NPV), с которым мы уже встречались в гл. 1 (§ 1.6). В принятых здесь обозначениях и с привязкой чистых поступлений к середине соответствующих периодов можно записать:
NPV = - K + [(p - c)Q - f]an;i (1 + i)0,5. (3.23)
По определению, в барьерной точке NPV = Q. Отсюда
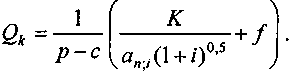 (3.24)
(3.24)Первое слагаемое в скобках равно члену финансовой ренты, современная стоимость которой равна сумме инвестиций.
Поток чистых поступлений можно расчленить без потери в точности для последующих расчетов на два потока — поступлений (положительные величины) и расходов (отрицательные величины). Соответственно при постоянных параметрах этих потоков имеем pQ и cQ + f. Графическая иллюстрация изменения современных стоимостей указанных потоков в зависимости от выпуска представлена на рис. 3.17.
ПРИМЕР 9
Применим оба метода анализа, бухгалтерский и финансовый, для анализа инвестиционного проекта, который характеризуется следующими данными: K = 1100, р = 50, с = 30, f = 5, d = 100, п = 10 лет. Дисконтирование осуществляется по ставке 12% годовых.
По формуле (3.21) находим
Qk =
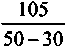 = 5,25.
= 5,25.В свою очередь, финансовый метод дает
Qk =
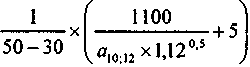 = 9,45.
= 9,45.Как видим, последний ответ существенно отличается от предыдущего.
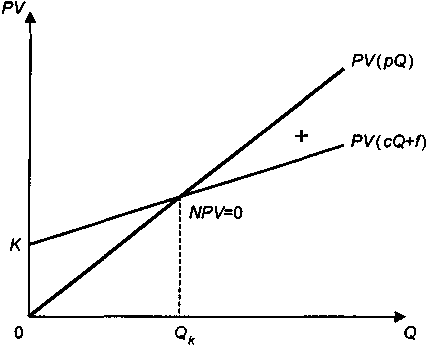
Рис. 3.17
При сравнении формул (3.21) и (3.24) становится очевидным, что расхождение в результатах оценки барьерной точки выпуска связано с тем, что
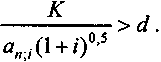
Иначе говоря, член ренты, амортизирующей капиталовложения, должен быть больше амортизационных отчислений. Равенство в приведенном соотношении будет наблюдаться только в случае, когда i = 0. В этом случае ап;0 = п.
При бухгалтерском подходе из поля зрения аналитика выпадает выгода от возможного иного пути использования ресурсов. В связи с этим введем важное в современной экономике понятие условной (вменённой) потери прибыли (opportunity costs) в результате неиспользования альтернативного курса действий. Для иллюстрации приведем следующий пример. Пусть ресурсом для конкретности является производственное здание. У владельца имеются две альтернативы его использования:
- осуществить некоторый производственный проект, предусматривающий использование этого здания;
- продать здание (или сдать его в аренду).
Если владелец реализует проект, то он теряет вторую возможность получения дохода. Таким образом, хотя при реализации проекта здание не приобретается, его стоимость должна включаться в инвестиционные издержки. Здесь уместно привести следующую иллюстрацию16. Компания Локхид обратилась в 1971 г. в Конгресс США по поводу убыточности производства военных самолетов TriStar L-1011. Обращение аргументировалось тем, что коммерческая привлекательность производства была определена с учетом барьерной точки выпуска в размере около 200 самолетов. Однако эта величина не учитывала ранее сделанных капиталовложений в сумме 1 млрд. долл. С учетом указанных вмененных затрат барьерная точка повышается до 500 самолетов.
