Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.

Вид материала

Книга

Содержание § 3.2. Нелинейные модели

Подобный материал:

• Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
• Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
• Планирование производственных запасов и определение потребности предприятия, 53.58kb.
• Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
• Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
• Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
• Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
• Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
• Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
• И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.

§ 3.2. Нелинейные модели

Линейная модель во многих случаях дает практически приемлемое описание ситуации. Однако могут возникать ситуации, когда процесс формирования затрат и (или) стоимости продукции более адекватно описывается нелинейными функциями и имеются достаточно надежные данные для получения соответствующих кривых. Вид и параметры таких кривых могут быть установлены, например, в ходе статистического анализа, или их можно задать экспертно.

Барьерный выпуск продукции. Вернемся к задаче по определению критического объема продукции, но в условиях, когда одна или обе "конкурирующие" функции являются нелинейными. Рассмотрим несколько возможных постановок задач. Пусть для начала стоимость продукции — линейная функция выпуска, а затраты на производство описываются нелинейной функцией. Предполагается, что удельные затраты сокращаются по мере роста масштабов производства, а цена единицы продукции не изменяется. Такое сочетание затрат и стоимости продукции представлено на рис. 3.3.

Стоимость продукции находится по формуле (3.1). Допустим, общая сумма переменных затрат описывается степенной функцией cQ^h , причем 0 < h < 1. В этом случае общая сумма затрат составит:

S = F + cQ^h.

Разность "конкурирующих" функций в барьерной точке равна нулю:



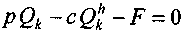
Решение сводится к нахождению корня этого выражения.


ПРИМЕР 2

Исходные данные: F = 100, р = 50, с = 40, h = 0,5. Соответственно имеем



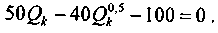
Получим Q_k = 3,5.



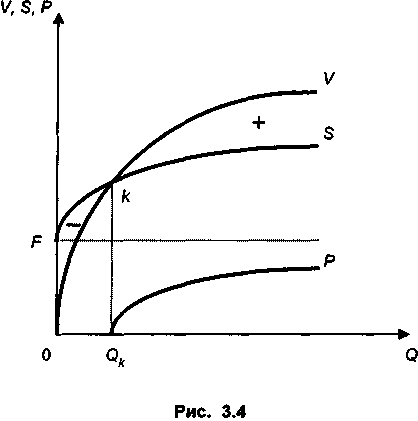
Сочетание двух нелинейных зависимостей, каждая из которых не имеет точки максимума, показано на рис. 3.4. Предполагается, что удельные затраты и цены сокращаются по мере роста выпуска продукции.

Например, если обе функции являются степенными:

V = pQ^m, S = F + cQ^h, m < 1, h < 1,

то искомый барьерный уровень находим на основе выражения



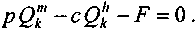
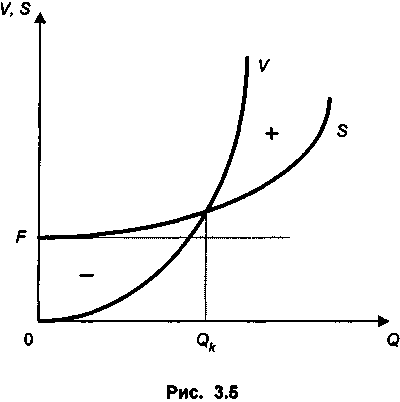
Пусть теперь обе функции являются параболами второй степени (рис. 3.5):

V = aQ² + bQ, S = cQ² + dQ + F,

где a, b, с, d — параметры парабол.

Прибыль в зависимости от уровня выпуска составит:

P = (a - c)Q² + (b - d)Q - F, (3.6)



а барьерный объем выпуска находится из уравнения



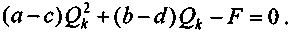
Добавим, что в рассмотренных условиях можно рассчитать объем выпуска, максимизирующего размер прибыли (обозначим его как Q_m). Для этого, как известно, достаточно найти производную функции прибыли и приравнять ее нулю. В случае, когда прибыль описывается выражением (3.6), находим




Как видим, положение точки максимума полностью определяется параметрами соответствующих парабол. Причем необходимым условием существования максимума являются следующие соотношения: d > b; a > с. Если b > d и а > с, то прибыль монотонно растет вместе с увеличением выпуска.

Нелинейную модель можно представить и в неформализованном виде — как таблицу данных, характеризующих затраты и стоимость продукции в зависимости от размера выпуска.




ПРИМЕР 3

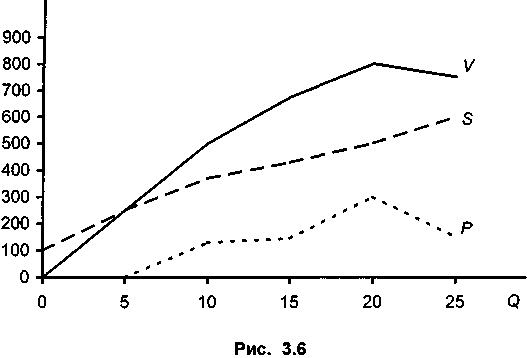
В приведенной ниже таблице и на диаграмме (рис. 3.6) содержатся данные о затратах, стоимости продукции и ожидаемой прибыли.

Q	F	c	p	S	V	Р
0	100	—	—	100	—	—
5	100	30	50	250	250	0
10	100	27	50	370	500	130
15	100	22	45	430	675	145
20	100	20	40	500	800	300
25	100	20	30	600	750	150

Барьерный выпуск равен 5. Наибольшая прибыль приходится на выпуск, равный 20.




Сравнение финансовых показателей на основе барьерных величин. Перейдем к решению простой задачи, иллюстрирующей возможности метода при решении некоторых проблем в финансово-кредитной области. Допустим, необходимо выбрать один из двух вариантов поступлений денежных средств: S₁; S₂ со сроками n₁; n₂, причем S₂ > S₁; п₂ > n₁, иначе постановка задачи не имеет экономического смысла — выбор очевиден. Решение основано на сравнении величин современной стоимости соответствующих денежных сумм. Таким образом, выбор зависит от существующего или ожидаемого уровня доходности денежных инвестиций в виде процентной ставки (управляющая переменная j). При выборе варианта следует ориентироваться на значение барьерной ставки¹⁴, т. е. ставки, при которой оба варианта оказываются равноценными по доходности.

Рассмотрим метод решения этой задачи для двух вариантов расчета современных стоимостей по простой и сложной процентным ставкам. Для определения барьерных уровней ставок найдем равенства "конкурирующих" функций — современных стоимостей двух платежей P₁ = P₂. Для простой ставки имеем

(3.7)

а для сложной —

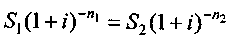, (3.8)

где i — величина барьерной ставки. Решив равенство (3.7), получим

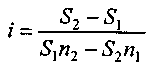(3.9)

Из выражения (3.9) находим необходимое условие для существования барьерной ставки:

S₁ n₂ > S₂ n₁, или.

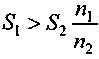Графическая иллюстрация решения представлена на рис. 3.7.



Как видно на рис. 3.7, при j < i предпочтителен вариант S₂


ПРИМЕР 4

S₁ = 1; S₂ = 1,15; n₁ = 7; п₂ = 12 (сроки платежей указаны в месяцах).

Находим 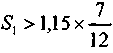, следовательно, решение существует. Получим

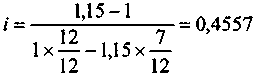, или 45,6%.

Таким образом, при рыночной простой ставке, меньшей 45,6%, предпочтительнее более отдаленная выплата при всех прочих равных условиях.

Перейдем к определению барьерного значения сложной ставки. На основе (3.8) находим

,

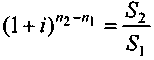откуда



В итоге

i = ant ln (1 + i) - 1. (3.10)


ПРИМЕР 5

S₁ = 1; S₂ = 1,4; n₁ = 1; п₂ = 2,5 (сроки платежей измерены в годах). Находим

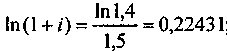; i = ant ln 0,22431-1 = 0,251.

При ставке, превышающей 25,1%, предпочтительнее оказывается первый вариант.