Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.

Вид материала

Книга

Содержание § 2.4. Нелинейные методы с начислением процентов на суммы амортизации P (условно назовем эту величину ценой участка), ожидаемый срок эксплуатации — n Метод аннуитетов

Подобный материал:

• Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
• Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
• Планирование производственных запасов и определение потребности предприятия, 53.58kb.
• Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
• Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
• Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
• Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
• Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
• Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
• И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.

§ 2.4. Нелинейные методы с начислением процентов на суммы амортизации

г) Метод накопленного резерва

Представим себе ситуацию, когда амортизационные суммы аккумулируются в особом резерве (фонде) для дальнейшего целевого использования — приобретения нового оборудования взамен изношенного. (В действительности эти деньги обычно "работают" в качестве текущих активов фирмы.) Причем, как и в любом другом случае накопления средств, на вложенные в этот резерв деньги начисляются проценты. Далее предположим, что в конце срока амортизации сумма накопленного резерва должна быть равна стоимости выбывшего оборудования с учетом ликвидационной стоимости. Пусть взносы, необходимые для создания резерва, постоянные. Тогда поток платежей представляет собой постоянную финансовую ренту постнумерандо, наращенная сумма которой равна необходимому резерву.

Перепишем формулу наращенной суммы постоянной ренты постнумерандо (1.9), использовав символы, принятые в данной главе.

Ds_n;i=P - L,

откуда сумма разового взноса в резерв

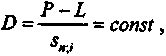(2.17)

где s_n;i — коэффициент наращения постоянной финансовой ренты.

Процесс увеличения резерва с учетом последовательных взносов в конце года и наращения процентов определяется как S_t=Ds_t;j,

где t — интервал от начала списания до момента оценки.

Из последнего выражения становится понятным, что сумма резерва ускоренно возрастает с каждым шагом во времени. Соответственно должны расти и амортизационные списания. Таким образом, за первый год износ составит величину D, за второй — D(1 + i) и т. д. Износ за год t определяется как D_t = D(1 + i)^t-1.

Указанные суммы списываются в конце каждого года с остаточной стоимости. Таким образом, балансовую стоимость на конец первого года после списания износа находим как

B₁ = P - D₁,

на конец второго года она составит:

B₂ = P - [D + D(1 + i)] = B₁ - D(1 + i) и т.д.

Для года t

B_t = P - Ds_t;i (2.18)

или, определяя последовательно,

B_t+1 = B_t - D_t.

Очевидно, что процесс амортизации по этому методу оказывается замедленным. Медианный срок приближенно можно найти из равенства



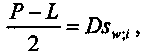
откуда



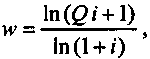
где

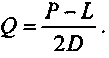
Отметим, что величина разового взноса в резерв меньше суммы амортизации по линейному методу. Причем, чем выше ставка, применяемая при накоплении, тем больше разница между суммой взноса D и годовым размером линейной амортизации.


ПРИМЕР 4

Для данных примера 1 при условии, что на аккумулируемые средства начисляются проценты по ставке 15% годовых, найдем сумму ежегодного взноса в резерв:

D = (100 - 4)/s_5;15 = 96/6,74238 = 14,238 .

Напомним, что по линейному методу годовая сумма амортизации равна в этом примере 19,2. Процесс формирования резерва и динамика балансовой стоимости показаны в таблице.

t	D	Dt	Dst;i	Bt
0	—	—	—	100,000
1	14,238	14,238	14,238	85,762
2	14,238	16,374	30,612	69,388
3	14,238	18,830	49,442	50,558
4	14,238	21,655	71,097	28,903
5	14,238	24,903	96,000	4,000
Итого		96,000

Как видим, в первые годы процесс списания балансовой стоимости здесь более медленный, чем при линейном начислении износа. Половина амортизируемой стоимости амортизируется за 3 года. Напомним, что по линейному методу w = 2,6.

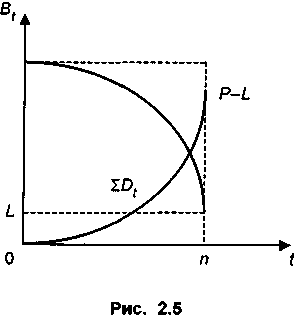
На рис 2.5 проиллюстрирован процесс увеличения износа и сокращения балансовой стоимости оборудования по методу накопленного резерва.

Метод накопленного резерва применяется и при решении задачи, непосредственно не связанной с расчетом сумм амортизации, но по своему содержанию близкой к нему. Познакомимся с проблемой в общем виде. Речь идет об использовании некоторого ограниченного ресурса, который имеется на начало процесса производства. Таким ресурсом чаще всего являются разрабатываемые запасы полезных ископаемых. Их истощение необходимо учитывать в себестоимости продукции (depletion allowance). Инвестор в процессе эксплуатации месторождения должен, во-первых, накопить денежный резерв для возобновления производства на новом участке, а во-вторых, получить прибыль от инвестиций в разработку месторождения.

Возможны две альтернативные постановки задачи. Первая заключается в определении цены объекта разработки, эквивалентной ожидаемому доходу при принятой норме доходности инвестиций. Вторая состоит в определении дохода, эквивалентного заданной цене. Остановимся только на второй постановке задачи.



Допустим, инвестиции в приобретение участка и его подготовку к разработке составили P (условно назовем эту величину ценой участка), ожидаемый срок эксплуатации — n лет. Если норма доходности инвестиций установлена в размере j процентов, а на перечисляемые в резерв средства начисляются проценты по ставке i, то отдача от инвестиций должна составить сумму Pj и для создания резерва необходимо выделять P/s_n;i . В целом ежегодные поступления определяются как

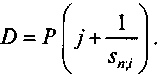(2.19)

В частном случае, когда ставки j и i оказываются одинаковыми, получим (см. § 2.6):

D = P/a_n;i , (2.20)

где a_n;i — коэффициент приведения постоянных рент постнумерандо.


ПРИМЕР 5

Пусть цена карьера (приобретение участка, его освоение и т. д.) составляет 100 млрд. руб., срок разработки — 5 лет, норма доходности от инвестиций — 15%, ставка процента при накоплении резерва — 20%.

Находим s_5;20 = 7,4416. Следовательно,



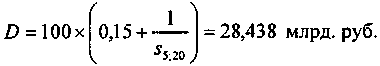
Из этой суммы 15 млрд. руб. представляют собой инвестиционный доход. Остальные деньги поступают в резерв.


д) Метод аннуитетов

Строго говоря, метод накопленного резерва, как, впрочем, и другие рассмотренные выше методы, противоречит принципу изменения ценности денег во времени. Дело в том, что накопленные в порядке амортизации средства, если они действительно накопляются, неэквивалентны в финансовом смысле затратам на приобретение оборудования. В самом деле, инвестор вкладывает в оборудование сумму P, амортизирует ее каким-либо способом в течение п лет и создает резерв в той же сумме P. Таким образом, инвестор, по крайней мере теоретически, несет некоторый ущерб. Иное дело, если при амортизации принимается во внимание необходимость начисления процентов на инвестируемые средства. В этом случае баланс между вложениями в оборудование и амортизационными списаниями достигается следующим образом:

P = Da_n;i + Lvⁿ,

откуда размер амортизационных затрат, включая процент на инвестированный капитал, составит:

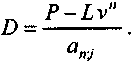(2.21)

Иначе говоря, модель износа базируется на таком же принципе, что и общепринятый метод обслуживания долга. Конкретно это означает, что затраты на приобретение оборудования рассматриваются как некоторая задолженность, растущая до момента первого списания износа. В этот момент часть суммы D идет на уплату процентов, а остаток — на погашение основного долга, т. е. на уменьшение балансовой стоимости. Процесс повторяется до полной амортизации стоимости оборудования.

Определим для года (t + 1) размер остаточной балансовой стоимости:

B_t+1 = b_t - (d - b_ti) = B_t (1 + i) - D. (2.22)

Разность в скобках равна сумме износа.


ПРИМЕР 6

По данным примера 1 при условии, что i = 15%, находим



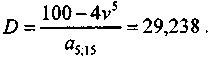
Для первого года B₁ = 100 - (29,238 - 15,000) = 85,762.

Размеры износа, расходы по амортизации и остаточная стоимость для конца каждого года показаны в таблице, где A = D - B_ti.

t	D	%	А	Bt
0	—	—	—	100,000
1	29,238	15,000	14,238	85,762
2	29,238	12,864	16,374	69,388
3	29,238	10,408	18,830	50,558
4	29,238	7,583	21,655	28,903
5	29,238	4,335	24,903	4,000
Итого		96,000