Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.

Вид материала

Книга

Содержание §1.4. Эквивалентные потоки платежей §1.5. Определение доходности на основе потока платежей D — размер инвестиций; R Т — средний срок. Средний срок в данной ситуации определяется элементарно: Т =п/

Подобный материал:

• Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
• Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
• Планирование производственных запасов и определение потребности предприятия, 53.58kb.
• Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
• Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
• Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
• Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
• Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
• Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
• И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.

§1.4. Эквивалентные потоки платежей

В финансовом анализе важную роль играет принцип эквивалентности, согласно которому платежи считаются эквивалентными, если их современные стоимости одинаковы. Сказанное справедливо и применительно к потокам платежей. Так, например, нерегулярный поток платежей и постоянная рента оказываются эквивалентными, если имеет место равенство



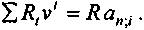
Коль скоро потоки платежей являются эквивалентными, замена одного потока другим не изменяет финансовое положение участвующих сторон. Пусть в контракте оговорен поток поступлений со значительными колебаниями их размеров. Возникла необходимость сравнения с конкурирующими условиями, предусматривающими выплату ренты с постоянными членами. Сроки и остальные условия у двух потоков платежей одинаковы. Определим неизвестный размер члена постоянной ренты R.

Напомним, что 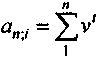. Таким образом: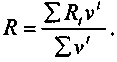



Как видим, R представляет собой среднюю арифметическую взвешенную с весами, равными дисконтным множителям. Пусть заменяющая рента в рассмотренном случае имеет срок n₁, отличающийся от п. Тогда



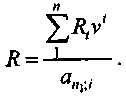
Аналогичным образом можно определить любой другой параметр заменяющего эквивалентного потока платежей. Заметим, что заменяющий поток может отличаться от заменяемого по всем параметрам и по виду. Например, дискретная рента может быть заменена непрерывной и т. д.

§1.5. Определение доходности на основе потока платежей

В § 1.2 мельком была затронута проблема определения размера процентной ставки по остальным параметрам потока платежей. Вернемся к этой проблеме применительно к определению доходности по основным инвестиционным схемам. Остановимся на трех из них:

• мгновенные (разовые) инвестиции, отдача в виде регулярного или нерегулярного потока платежей;
  
• инвестиции в финансовый инструмент (облигацию), постоянная отдача (купонный доход) и возврат номинала в конце срока;
  
• инвестиции в финансовый инструмент (долговое обязательство, кредит), последовательное обслуживание долга (равные суммы погашения основного долга и периодическая выплата процентов).
  

Во второй и третьей схемах предусматриваются два источника дохода: доход от прироста капитала в виде разности между суммой номинала инструмента и его ценой (capital gain) и начисленные проценты.

Условия перечисленных схем можно кратко записать как



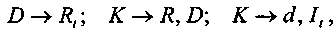
где D — размер инвестиций;

R_t, R — члены потока поступлений;

K — цена (или курс) финансового инструмента;

d — размер разового погашения долга;

I_t, — сумма процентов за период.

Приведем уравнения эквивалентности, с помощью которых определяются показатели доходности (в виде процентных ставок) соответствующих инвестиционных схем. Для первой схемы имеем:

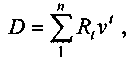(1.30)

где дисконтные множители определяются по искомой процентной ставке j.


ПРИМЕР 14

Сумма мгновенных инвестиций — 100, срок — 5 лет, поступления — в конце каждого года. Как видно из расчета, представленного в нижеследующей таблице, эквивалентность инвестиций и отдачи имеет место в случае, когда дисконтирование производится по ставке 21,46%. Последний показатель характеризует доходность финансовой операции.

t	Rt	vt	Rtvt
1	20	0,82332	16,46633
2	30	0,67785	20,33549
3	60	0,55808	33,48509
4	40	0,45948	18,37921
5	30	0,37830	11,34893
Итого	—	—	100,01500

Если отдача постоянна, то вместо (1.30) имеем

D = Ra_n;j. (1.31)

Величина у рассчитывается по коэффициенту приведения постоянной ренты:



Заметим, что положительное и отличное от нуля значение показателя доходности имеет место в случае, когда a_n;j < п . Соответственно R/D > п.

Вторая из упомянутых инвестиционных схем пригодна для инвестиций в облигации⁹ с периодическими выплатами постоянного купонного дохода и погашением обязательства в конце срока по номиналу. Для этих условий получим следующее уравнение эквивалентности при условии, что купоны погашаются ежегодно:

P = Ra_n;j+Nvⁿ, (1.32)

где R = Ni;

i — уровень купонного дохода;

Р — цена облигации;

N — номинал.

Если под Р подразумевается курс облигации (P = K), то N= 100.

Для оценки доходности можно применить и приближенную формулу

(1.33)

В формуле (1.33) средний годовой доход от облигации соотносится с ее ценой, средней за весь срок. За простоту расчета, впрочем, приходится платить потерей точности оценки.


ПРИМЕР 15

Облигация со сроком 5 лет, проценты по которой выплачиваются один раз в год по норме 8%, куплена по курсу 97. Запишем уравнение эквивалентности (1.32) и разделим обе его стороны на 100:

0,97 = (1 + j)^-5 + 0,08 a_5;j.

С помощью линейной интерполяции находим j = 8,77%. Для проверки рассчитаем курс на основе полученной ставки. Находим



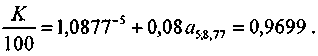
Как видим, расчетный курс весьма близок к рыночному 97. Приближенное решение по (1.33) дает



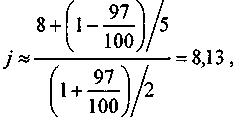
что соответствует рыночному курсу 0,74. Погрешность заметно выше, чем при использовании линейной интерполяции.

Уравнение эквивалентности для третьей схемы (ежегодные выплаты сумм обслуживания долга без льготного периода) имеет вид:

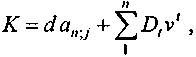(1.34)

где 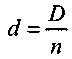— годовой размер погашения долга;

D_t — остаток долга на начало года t, D₁ = D, D_t = D_t-1- d.

Для быстрой ориентации в сложившейся ситуации иногда прибегают к приближенному методу оценки доходности как суммы двух составляющих:



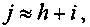
где h — доходность от разности номинала и цены;

i — процентная ставка по условиям финансового инструмента.

При определении первого элемента этой суммы фактический процесс последовательного погашения долга условно заменяется разовым погашением со средним сроком выплаты. Из равенства

K = Dv^T

следует, что



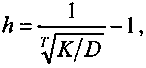
где Т — средний срок.

Средний срок в данной ситуации определяется элементарно: Т =п/2 . Наличие льготного периода (без погашения основного долга) увеличивает средний срок на соответствующую величину.


ПРИМЕР 16

Финансовый инструмент (номинал 100) куплен за 75. Погашение долга в течение 5 лет равными платежами, проценты по ставке 10% годовых. Какова финансовая эффективность операции?

Находим 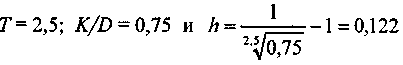. Таким образом,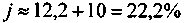

Точная величина доходности равна 23,11%. Расчет современной стоимости поступлений по этой ставке представлен в таблице, в которой символом R_t обозначена ежегодная сумма обслуживания долга.

t	Dt	Rt	vt	Rtvt
1	100	30	0,909091	24,368450
2	80	28	0,826446	18,474440
3	60	26	0,751315	13,934560
4	40	24	0,683013	10,448110
5	20	22	0,620921	7,779578
Итого	—	—	—	75,005150

С увеличением отклонения K от 100 растет погрешность оценки. Аналогичное можно утверждать и по поводу влияния процентной ставки и срока погашения долга.