Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.

Вид материала

Книга

Содержание § 6.3. Индекс доходности § 6.4. Соотношения относительных измерителей эффективности

Подобный материал:

• Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
• Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
• Планирование производственных запасов и определение потребности предприятия, 53.58kb.
• Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
• Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
• Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
• Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
• Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
• Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
• И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.

§ 6.3. Индекс доходности

Рентабельность инвестиций может быть измерена двумя путями — бухгалтерским и с учетом фактора времени (с дисконтированием членов потока платежей). В обоих случаях доход сопоставляется с размером инвестиций. Так, на основе бухгалтерского метода получим два варианта индекса доходности:

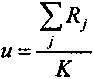(6.13)

или

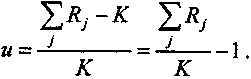(6.14)

В последней записи этот индекс полностью совпадает с принятым у нас показателем рентабельности.

Интересно проследить влияние взаимозависимости бухгалтерского срока окупаемости и показателя рентабельности. Для этого обратимся к случаю, когда доходы постоянны во времени. Упомянутые показатели определяются на основе следующих равенств:

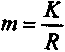и ,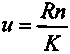

откуда следует:

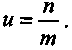(6.15)

Рентабельность и срок окупаемости находятся в обратной зависимости.

При дисконтировании членов потока платежей индекс доходности определяется следующим образом:

если капиталовложения приведены к одной сумме K, то

;

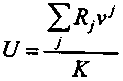если же капитальные затраты распределены во времени, то

(6.16)


ПРИМЕР 8

По данным примера 1 (см. § 5.2), приведенные к началу срока инвестиционного проекта капиталовложения для варианта А составили 214,9, а доход — 377,1. Для варианта Б — соответственно 223,1 и 383,5. Показатели рентабельности

U_A = 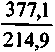= 1,754; U_Б = 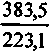= 1,719.

Если поток доходов представляет собой постоянную ренту постнумерандо, а капиталовложения мгновенны, то

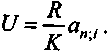(6.17)


ПРИМЕР 9

Поток доходов и остальные условия инвестирования показаны в примере 3. Определим индекс доходности в случае, когда дисконтирование производится по ставке 10%.

U = 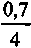a_10;10 = 1,183.

Аналогичным путем можно определить рентабельность и для иных видов распределения доходов во времени.

§ 6.4. Соотношения относительных измерителей эффективности

Относительные финансовые показатели эффективности инвестиций имеют сходную задачу и базируются в конечном счете на одной методике — сопоставлении доходов и затрат. Однако каждый из них решает задачу под своим углом зрения. Можно ожидать, что подобные измерители взаимосвязаны, причем в общем динамика одного показателя непропорциональна изменению другого. Знакомство с такими зависимостями полезно для лучшего понимания существа рассмотренных показателей и их применения в практических ситуациях.

Зависимости между попарно взятыми показателями эффективности легко выявить аналитическим путем для случаев, когда поток доходов может быть представлен в виде дискретной финансовой ренты, а капиталовложения мгновенны. Для того чтобы обнаружить интересующие нас связи в общем виде, этого достаточно.

Ниже приведены две группы соотношений: между дисконтированными показателями эффективности, между дисконтированными и бухгалтерскими измерителями. Доказательство каждого из этих соотношений базируется на принципе финансовой эквивалентности (см. § 6.9).

Начнем с двух важнейших показателей первой группы — чистого приведенного дохода и внутренней нормы доходности.



Рис. 6.6


На основе формул (5.1) и (5.2) находим следующую зависимость:

N = R(a_n;i - а_n;J). (6.18)

Здесь i — ставка, которая применяется при определении чистого приведенного дохода N. Величина N оказывается положительной, если i < J. Графическая иллюстрация данной зависимости представлена на рис. 6.6.

Зависимость внутренней нормы доходности и дисконтированного срока окупаемости определяется следующим образом (см. § 6.9):

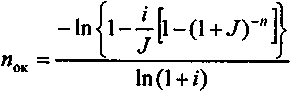. (6.19)

С повышением срока окупаемости внутренняя норма доходности сокращается. График этой зависимости представлен на рис. 6.7.

Зависимость внутренней нормы доходности и индекса доходности получим на основе формул (5.2) и (5.4):

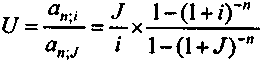. (6.20)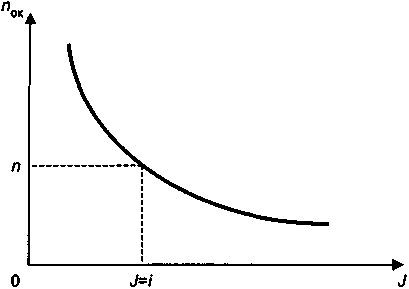



Рис. 6.7


Графическая иллюстрация данного соотношения показана на рис. 6.8. Как следует из формулы (6.20), при J = 0 имеем U = 0, при J = i имеем U = 1; наконец, если J > i, то U > 1.



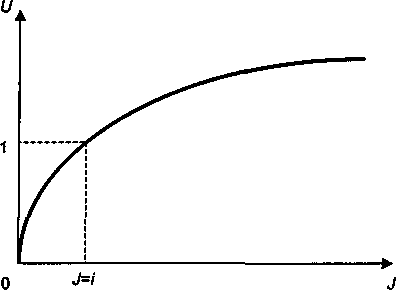
Рис. 6.8


Последняя зависимость этой группы — индекс доходности и срок окупаемости. На основе (5.3) и (5.4) имеем

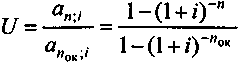. (6.21)

График зависимости представлен на рис. 6.9.



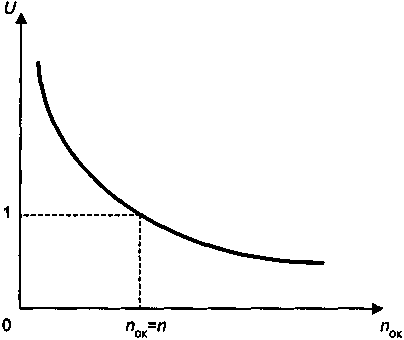
Рис. 6.9


Остановимся теперь на некоторых соотношениях показателей второй группы. Найдем соотношения рентабельности с индексом доходности, дисконтированным сроком окупаемости и внутренней нормой доходности.

; ; .

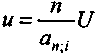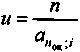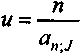Две первые зависимости иллюстрируются на рис. 6.10. Рентабельность прямо пропорциональна индексу доходности. Коэффициент пропорциональности больше единицы и зависит от размера ставки i. Напомним, что при i = 0 a_n;i = n.

Рассмотрим соотношения срока окупаемости и дисконтированных показателей эффективности (зависимость т и п_OK была показана выше, см. (6.12)). Получим:

; т = a_n;J .

Срок окупаемости обратно пропорционален индексу доходности и равен коэффициенту приведения ренты, рассчитанному по внутренней норме доходности. Графики соответствующих зависимостей см. на рис. 6.11.



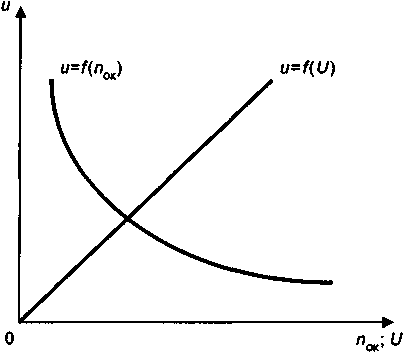
Рис. 6.10


Приведенные соотношения получены для частного случая, когда капиталовложения мгновенны, а отдача от них представляет собой ограниченную постоянную ренту постнумерандо. В действительности поток доходов далеко не всегда следует указанной закономерности, отклоняясь от нее в ту или иную сторону. В силу этого найденные строгие зависимости "размываются".



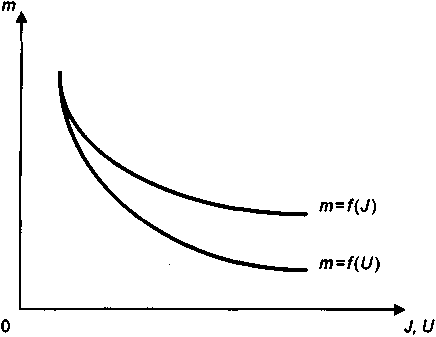
Рис. 6.11