Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.
| Вид материала | Книга |
- Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
- Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
- Планирование производственных запасов и определение потребности предприятия, 53.58kb.
- Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
- Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
- Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
- Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
- И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.
§ 7.5. Факторы, влияющие на размеры лизинговых платежей
Поскольку при заданной цене имущества размер лизингового платежа зависит от величины коэффициента рассрочки, в котором "сконцентрированы" все основные условия лизинга, то имеет смысл остановиться на факторах, определяющих его размер.
Очевидно, что с увеличением срока лизинга коэффициент рассрочки уменьшается. В пределе при
 получим a = i (рис. 7.3).
получим a = i (рис. 7.3).Как показано на рис. 7.3 влияние срока лизинга заметно сказывается в начале шкалы. Это иллюстрируется следующими данными, подсчитанными для i = 5% и платежей постнумерандо:
| n | 4 | 8 | 16 | 20 | 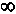 |
| a | 0,28201 | 0,15472 | 0,09227 | 0,08024 | 0,05 |
При заданных размерах процентной ставки и срока лизинга увеличение доли остаточной стоимости линейно уменьшает величину коэффициента рассрочки.
Что касается процентной ставки, то, очевидно, чем она выше, тем больше коэффициент рассрочки, причем при i = 0 имеем a = 1/n (см. рис. 7.4). Влияние ставки усиливается вместе с ростом размера ставки. Так, для n = 12 находим
| i | 0 | 5 | 10 | 15 |
| а | 0,08333 | 0,11283 | 0,14676 | 0,18448 |
ПРИМЕР 9
Если в примере 1:
• сократить срок лизинга с 5 до 3 лет (на 40%), то а = 0,40211 и R = 40,211 (т. е. произойдет увеличение платежа на 52%);
• увеличить процентную ставку вдвое (с 10 до 20%), то а = 0,33438 и R = 33,438, т. е. имеет место увеличение на 26, 8%.
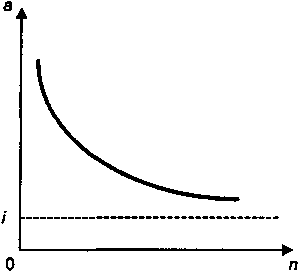
Рис. 7.3
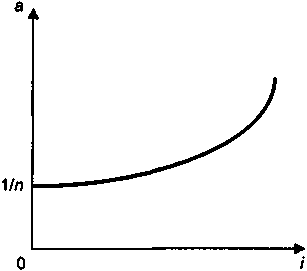
Рис. 7.4
Выше процентная ставка i использовалась как некий "технический" параметр для дисконтирования платежей и начисления процентов. Если все параметры операции, кроме лизингового платежа, заданы в контракте, то управляющим параметром при расчете размера лизинговых платежей является уровень процентной ставки. В то же время если в контракте заданы размеры лизинговых платежей, то i характеризует общую доходность инвестиций в лизинговую операцию. Пусть теперь имущество приобретено за счет привлеченных средств, причем за кредит выплачиваются проценты по ставке r, тогда доходность от предпринимательской деятельности лизингодателя, или финансовая эффективность лизинга р, составит: p = i - r.
ГЛАВА 8 ИНТЕРВАЛЬНОЕ ЭКСПЕРТНОЕ ПРОГНОЗИРОВАНИЕ
Случайность — запасной фонд Господа Бога.
Всемогущий прибегает к нему лишь в тех
важных случаях, особенно теперь,
когда люди стали так проницательны,
что предвидят грядущее, наблюдая природу
и постигая ее закономерности.
А. Дюма
Если Вы когда-нибудь угадали,
никогда не позволяйте забыть это.
Из правил прогнозиста
§ 8.1. Основные элементы методики
Для количественного анализа инвестиций в производство необходим достаточно большой объем информации. Часть ее обеспечивается технико-экономическими расчетами и накопленной производственной статистикой. Однако многие данные, особенно при разработке крупных проектов, можно получить лишь экспертным путем. Существование значительных диапазонов для реально возможных будущих состояний объекта прогноза требует разработки не точечных, а интервальных экспертных прогнозов и наделения последних субъективными вероятностями их реализации (осуществления). Чем больше эта вероятность, тем шире интервал прогноза при всех прочих равных условиях. Кратко методика сводится к "извлечению" из эксперта некоторых суждений и их преобразованию в более узкие интервалы прогноза, чем это первоначально было задано экспертом для некоторых крайних ситуаций.
Определение интервала для прогнозируемой величины и его увязывание с вероятностью реализации можно во многих случаях сделать вполне выполнимой задачей, если воспользоваться предлагаемой ниже методикой41. Данная методика отличается прагматичностью: она проста в реализации и не требует от эксперта глубоких знаний в области теории вероятностей и математической статистики. Достаточно быть знакомым с основными параметрами статистических распределений (средней, модой, дисперсией). Однако за простоту, как правило, надо платить. Плата заключается в нестрогом применении положений математической статистики. Последнее, впрочем, оправдывается и тем, что сами исходные данные обычно не являются результатами статистических наблюдений.
Согласно данной методике в задачу эксперта входят:
• определение реально возможного диапазона значений прогнозируемой величины;
• выбор вида распределения вероятностей реализации в пределах этого диапазона;
• выбор уровня надежности прогноза (вероятности его реализации).
Кроме того, при прогнозировании сумм или произведения показателей эксперт должен вынести суждение о наличии (или отсутствии) значительной зависимости слагаемых или сомножителей (да, нет). Это суждение выносится исходя из содержания рассматриваемых показателей, накопленного опыта или, в лучшем случае, основывается на результатах предварительного регрессионного или корреляционного анализа статистических данных.
Кратко охарактеризуем перечисленные этапы.
Реально возможный диапазон (РВД) — полный интервал реально возможных значений, в котором с практически 100%-й вероятностью (наверняка) окажется, по мнению эксперта, соответствующая характеристика. Эксперт для этого определяет экстремальные значения показателя (нижнюю и верхнюю границу) исходя из крайних сценариев развития исследуемого объекта. Пример: ожидается, что при наихудшей конъюнктуре для продавца цена продукции не может быть меньше А, при наилучшей — не более Б, или темп роста производства в некотором временном интервале не опустится ниже а% и не превысит b%.
Ожидаемый вид распределения вероятностей для прогнозируемой величины в пределах установленного РВД. Эксперт должен вынести самое общее суждение о виде распределения, выбрав один из четырех вариантов. Предлагаются следующие виды распределений: а) нормальное; б) треугольное; в) трапециевидное; г) равномерное. Для упрощения полагаем, что распределения б) и в) являются симметричными. (Можно было бы рассмотреть и несимметричные варианты этих распределений, однако вряд ли эксперт сможет более или менее удовлетворительно определить необходимые для этого параметры.) Заметим, что распределения б) и в) не встречаются в "классической" статистике.
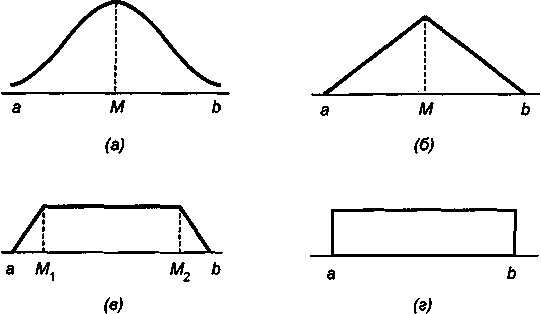
Рис. 8.1
(а) Нормальное распределение N. Ожидается, что варианты значений прогнозируемого параметра сосредоточены около среднего значения. Значения параметра, существенно отличающиеся от среднего, т. е. находящиеся в "хвостах" распределения, имеют малую вероятность осуществления.
(б) Треугольное распределение Т. Этот вид распределения можно рассматривать как некоторый суррогат нормального в тех случаях, когда известно только, что распределение симметрично и имеет одну моду, причем следует ожидать, что вероятность реализации более или менее равномерно растет по мере приближения к моде.
(в) Трапециевидное распределение Тр. Предполагается, что в пределах РВД существует интервал значений с наибольшей вероятностью реализации (НВР). Например, предполагается, что в диапазоне от 10 до 30% наиболее вероятны процентные ставки в пределах 15-25%.
(г) Равномерное распределение P. По мнению эксперта, все варианты прогнозируемого показателя имеют одинаковую вероятность реализации, что равносильно отсутствию каких-либо дополнительных экспертных суждений о характере явления.
По-видимому, наибольшую информацию эксперт должен иметь для того, чтобы утверждать, что распределение близко к нормальному42, и, наоборот, при полном отсутствии такой информации логично остановиться на равномерном распределении. Распределения Т и Тр занимают промежуточные места. Графическая иллюстрация перечисленных распределений приведена на рис. 8.1, на котором буквенные символы обозначают:
a, b — границы РВД;
М — модальное значение переменной;
M1 , M2 — границы НВР.
При использовании указанных распределений, кроме нормального, полагаем, что площадь под кривой распределения равна 1, или 100%. С небольшой натяжкой сказанное можно отнести и к нормальному распределению.
Третьим необходимым элементом методики является доверительная вероятность (ДВ), которая характеризует уровень вероятности реализации прогноза. Например, допустим, что интервальная оценка цены продукции в рамках прогноза считается надежной, если ДВ принята на уровне 0,9. Таким образом, в 9 случаях (шансах) из 10 (иными словами, с 90%-й вероятностью) можно утверждать, что прогноз окажется оправданным. Чем больше величина ДВ, тем ближе интервальный прогноз к РВД.
