Книга посвящена анализу производственных инвестиций (долгосрочных капиталовложений в производственный процесс) и прежде всего измерению их эффективности, сравнению производственных проектов и ряду смежных проблем.
| Вид материала | Книга |
- Конспект лекций по дисциплинам «Технология рэс» специальности 210201, 2303.43kb.
- Лившиц Вениамин Наумович «Особенности оценки эффективности производственных инвестиционных, 381.16kb.
- Планирование производственных запасов и определение потребности предприятия, 53.58kb.
- Инструкция по расчету и анализу технологического расхода электрической энергии на передачу, 383.13kb.
- Ммаэ-2 Теория и практика построения производственных функций, 207.53kb.
- Ированной образовательной программе повышения квалификации «Оценка экономической эффективности, 46.83kb.
- Отчет о проведении производственных испытаний эффективности биопрепарата фитоспорин-м, 64.89kb.
- Понятие, классификация и оценка материально-производственных запасов понятие материально-производственных, 106.29kb.
- Методическое пособие и регламент проведения проектных сессий по рассмотрению, анализу, 256.49kb.
- И. В. Суслина национальный исследовательский ядерный университет «мифи» проблемы корректной, 7.45kb.
§ 8.2. Методы определения интервальных прогнозов
После установления РВД и выбора вида распределения и уровня ДВ расчет границ интервального прогноза становится чисто технической задачей. Ее решение заключается в отсечении "лишних" концов РВД соответственно принятой доверительной вероятности. Иначе говоря, находят величины
А = а + х; B =b - x ,
где x — величина, зависящая от вида распределения и вероятности неудачи (неосуществления прогноза); очевидно, что упомянутая вероятность равна 1 - ДВ. Площади под кривой распределения, отсекаемые от "хвостов", равны половине этой вероятности (см. рис. 8.2) для треугольного распределения:
. (8.1)Значения этой вероятности для некоторых уровней ДВ приведены в табл. 8.1.
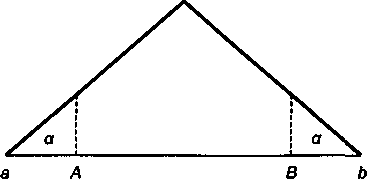
Рис. 8.2
Таблица 8.1
| ДВ, % | 60 | 70 | 75 | 80 | 90 |
| a | 0,2 | 0,15 | 0,125 | 0,1 | 0,05 |
Из сказанного следует, что задача определения интервального прогноза сводится к расчету размера x. Методики разработаны для следующих ситуаций:
А. Объект прогнозирования — отдельная количественная характеристика. Эксперт указывает РВД, вид распределения, а для распределения Тр и интервал наиболее вероятных значений прогнозируемого показателя.
Б. Прогноз суммы показателей,
. Например, сумма объемов выпуска нескольких видов продукции. Для каждого слагаемого указывается РВД и вид распределения. ДВ назначается только для итоговой суммы.В. Прогноз произведения двух показателей, Y = vw. Например, произведение "нормативного" и объемного показателей. Эксперт указывает РВД, вид распределения и ДВ для каждого сомножителя.
На первый взгляд представляется, что обсуждаемую методику легко распространить на прогноз суммы произведений. Формально это несложно выполнить. Однако, как показали расчеты, степень "сжатия" прогнозного интервала в этих условиях весьма мала, так что применение данной методики не имеет смысла.
Покажем технику применения перечисленных методик для каждого из указанных распределений вероятностей.
МЕТОДИКА А. Расчет интервального прогноза отдельной характеристики
Распределение N.
Известно, что площадь под кривой нормального распределения в пределах
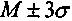примерно равна 99%. Отсюда
,где М — средняя,
— стандартное (среднее квадратическое) отклонение.Пусть z — нормированное отклонение от средней43, зависящее от выбранной доверительной вероятности. Тогда нормированное значение искомой величины x составит:
, (8.2)где
u = 3 - z. (8.3)
Вероятности невыполнения прогноза в каждом "хвосте" нормального распределения составят:
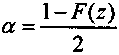. (8.4)Заметим, что для нормального распределения ДВ = F(z).
В табл. 8.2 44 приводятся значения z, и,
в зависимости от уровня ДВ.Таблица 8.2
| ДВ(%) | 68 | 75 | 80 | 85 | 90 | 95 |
| Z | 1 | 1,15 | 1,28 | 1,44 | 1,65 | 1,96 |
| U | 2 | 1,85 | 1,72 | 1,54 | 1,35 | 1,04 |
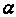 | 0,16 | 0,125 | 0,1 | 0,075 | 0,05 | 0,025 |
Необходимое для расчета по формуле (8.2) значение
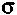находим следующим образом:
. (8.5)Распределение Т.
Искомая величина находится как функция от L и
:
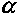. (8.6)Распределение Тр.
Здесь возможны два варианта. Если
, то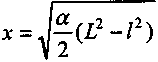
, (8.7)где l = М2 - М1 .
Если же
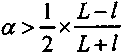, то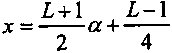
, (8.8)Распределение Р.
. (8.9)ПРИМЕР 1
Ожидается, что РВД (допустим, речь идет о годовом размере добычи минерального сырья) оценивается экспертом в объеме 1,2 — 1,8 млн. т. Определим интервальный прогноз для всех перечисленных выше видов распределений при условии, что ДВ = 80%. Для принятого уровня доверительной вероятности
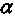= 0,1.Распределение N. L = 1,8 - 1,2 = 0,6;
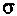= 0,6/6 = 0,1; u = 1,72 (см. табл. 8.2). По формуле (8.2) получимx = 1,72 x 0,1 = 0,172.
Таким образом, прогнозный интервал имеет пределы:
А = 1,2 + 0,172 = 1,37; B = 1,8 - 0,172 = 1,63.
Распределение Т. По формуле (8.6) находим
x = 0,6 х
=0,134 ,откуда
A = 1,2 + 0,134
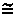1,33; B = 1,8 - 0,134 
1,67.Распределение Тр. Пусть интервал наиболее вероятных значений находится в пределах 1,35-1,65, l = 0,3. Поскольку
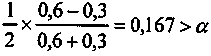,применяется формула (8.7):
;А = 1,2 + 0,12 = 1,32; В = 1,8 - 0,12 = 1,68.
Распределение Р.
x = 0,1 х 0,6 = 0,06;
А = 1,2 + 0,06 = 1,26; В = 1,8 - 0,06 = 1,74 .
Как видим, распределения N, Т и Тр дали примерно одинаковые интервалы для прогноза, а распределение Р — более "размытый" вариант.
МЕТОДИКА Б. Прогноз суммы показателей
Рассматриваются два варианта постановки задачи, когда слагаемые — это независимые величины и когда они зависимы друг от друга45.
Независимые слагаемые. Прогнозируемый показатель представляет собой сумму некоторых однородных величин. Слагаемые — независимые или слабо зависимые между собой показатели. Определение прогнозного интервала предполагает выполнение следующих последовательных шагов:
• установление РВД и определение видов распределений (напомним, что все они симметричные);
• расчет средних значений этих распределений и дисперсий;
• расчет общей средней (суммы частных средних) и дисперсии суммы;
• оценка границ интервального прогноза.
Формулы для расчета средних и дисперсий приведены в табл. 8.3 46.
Таблица 8.3
| Распределение | Средняя | Дисперсия |
| N | a + L/2 | (L/6)2 |
| Т | a + L/2 | L2/24 |
| Тр | а + L/2 | (L2 + l2)/24 |
| Р | a + L/2 | L2/12 |
Во всех приведенных в таблице формулах L = b - a .
Расчет суммы средних и дисперсии суммы производится следующим образом:
• сумма частных средних
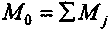; (8.10)• дисперсия суммы
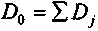, (8.11)где Мj, Dj — средние значения и дисперсии частных распределений;
• стандартная ошибка
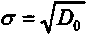. (8.12)Интервал прогноза определяется как
, (8.13)где z (нормированное отклонение) находится по табл. 8.2 или табл. 5 Приложения в зависимости от принятой ДВ.
ПРИМЕР 2
Эксперты установили следующие РВД и виды распределений для четырех слагаемых (в целях иллюстрации метода приняты различные виды распределений):
| Слагаемое | а | b | L | Распределение |
| 1 | 10 | 12 | 2 | Т; М = 11 |
| 2 | 50 | 55 | 5 | Тр; НВР = 52 - 53 |
| 3 | 8 | 13 | 5 | Р |
| 4 | 20 | 24 | 4 | Т; М = 22 |
| Сумма | 88 | 104 | — | — |
Полученные по этим данным значения частных средних и дисперсий приведены в следующей таблице.
| Слагаемое | Средняя | Дисперсия |
| 1 | 11 | 22/24 = 0,177 |
| 2 | 52,5 | (52 + 12)/24 = 1,08 |
| 3 | 10,5 | 52/12 = 2,08 |
| 4 | 22 | 42/24 = 0,677 |
| Сумма | 96 | 4,01 |
Пусть доверительная вероятность равна 75%, F(z) = 0,75. По табл. 8.2 находим z = 1,15; в свою очередь, получим
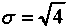= 2 .Нижняя и верхняя границы прогнозного интервала равны:
A = 96 - 1,15 x 2 = 93,7; B = 96 + 1,15 x 2 = 98,3.
Как видим, интервал прогноза заметно уже, чем суммы граничных значений РВД слагаемых (88 — 104), но вероятность "попадания" в него также меньше (не 100, а 75%).
Сильная зависимость между слагаемыми. Теоретически обоснованное решение проблемы требует в этой ситуации измерения коэффициентов корреляции между попарно взятыми случайными переменными (в нашем случае — слагаемыми). Поскольку следует ожидать в основном положительной корреляции, то дисперсия увеличивается. Следовательно, увеличивается и интервал прогноза. Например, если в примере 2 полагать, что коэффициенты корреляции у всех пар слагаемых одинаковы и равны, допустим, 0,9 (сильная положительная корреляция), то стандартная ошибка увеличится почти в 2 раза и составит 3,91 вместо 2. Искомый интервал в этом случае равен 91,5—100,5. Однако в такого рода задачах вряд ли практически возможен расчет коэффициентов корреляции (хотя бы в связи с отсутствием необходимой информации), поэтому целесообразно поступить иным образом, избежав тем самым расчет упомянутых коэффициентов.
Для решения задачи определим граничные значения прогнозных интервалов для каждого слагаемого, применив методику А. Обозначим эти величины как Aj и Bj. Искомые граничные значения для суммы составят:
.Слагаемые этих сумм рассчитаем с учетом того, что вероятности реализации прогноза для каждого слагаемого должны быть больше доверительной вероятности для суммы в целом. ДВ для суммы составит
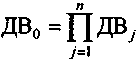.Для отдельного слагаемого ДВ определяется как
. (8.14)ПРИМЕР 3
Используем данные примера 2 и найдем интервальный прогноз для суммы теперь уже зависимых слагаемых при условии, что коэффициенты корреляции неизвестны. Примем, что ДВ для суммы равна 75%. Соответственно для отдельного слагаемого
ДВj =
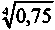= 0,93 . По формуле (8.1) находим 
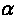= 0,035. Результаты расчетов величин x, vj и wj представлены в следующей таблице.| Слагаемое | Распределение | а | b | L(I) | Формула | x | Aj | Bj |
| 1 | Т | 10 | 12 | 2 | (8.6) | 0,26 | 10,26 | 11,74 |
| 2 | Тр | 50 | 55 | 5(1) | (8.8) | 1,01 | 51,01 | 53,99 |
| 3 | Р | 8 | 13 | 5 | (8.9) | 0,18 | 8,18 | 12,82 |
| 4 | Т | 20 | 24 | 4 | (8.6) | 0,53 | 20,53 | 23,47 |
| Сумма | | 88 | 104 | — | — | — | 89,98 | 102,02 |
МЕТОДИКА В. Прогноз произведения двух параметров
Иногда прогнозируемый показатель представляет собой произведение двух величин Y = VW , где одна величина — качественная характеристика (производительность труда, фондоотдача и т. п.), вторая — объемная величина (количество отработанного времени, размер фондов и пр.). Показатель Y прогнозируется не непосредственно, а на основе прогнозов сомножителей. Если рассматривать сомножители как независимые величины (а в большинстве случаев это правомерно), то методика сводится к следующему.
1. Для каждого сомножителя находится интервальный прогноз: V1, V2; W1,W2. При этом доверительная вероятность принимается на уровне P. Причем
.Иначе говоря, прогноз сомножителей должен быть сделан с большей доверительной вероятностью, чем прогноз итогового показателя (см. табл. 8.4; в ней же приводятся соответствующие значения
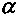).Таблица 8.4
| ДВ(%) | 60 | 70 | 75 | 80 | 90 | 95 |
| р (%) | 77,5 | 83,7 | 86,6 | 89,4 | 94,9 | 97,5 |
 | 0,112 | 0,082 | 0,067 | 0,053 | 0,026 | 0,013 |
2. Рассчитываются граничные значения прогнозного интервала как произведения V1W1, V2W2. С вероятностью ДВ можно утверждать, что реальное значение Y будет находиться в указанных пределах.
Можно применить и иной подход, взяв за базу средние распределений. Тогда последовательно находим: средние и дисперсии каждого распределения, произведение средних и дисперсию произведения. Последняя рассчитывается следующим образом47:
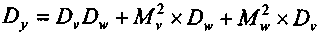, (8.15)где Dj и Mj — дисперсия и средняя.
ПРИМЕР 4
Прогнозируется произведение двух случайных переменных, РВД которых показаны ниже в таблице. Доверительная вероятность принята на уровне 80%. Таким образом, Р = 100
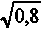= 89,4% . По табл. 8.4 находим 
= 0,053.Применим первый из рассмотренных выше подходов. По формулам (8.6) и (8.9) определим значения х и границы прогнозных интервалов для каждого сомножителя.
| | Распределение | а | b | L | x | А | B |
| V | T | 3 | 5 | 2 | 0,33 | 3,33 | 4,67 |
| W | P | 10 | 14 | 4 | 0,21 | 10,21 | 13,79 |
| Y | | | | | | 34,00 | 64,40 |
Как видим, прогнозный интервал 34 — 64,4 довольно широк. Однако он уже, чем произведение граничных значений РВД (30 — 70).
Для применения второго метода рассчитаем средние и дисперсии.
| | Средняя | Дисперсия |
| V | 4 | 0,167 |
| W | 12 | 1,333 |
| Y | 48 | 7,56 |
Для принятого уровня доверительной вероятности z = 1,28 (см. табл. 8.2). Границы прогнозного интервала составят:
А = 48 -1,28 x 7,56 = 38,32; B = 48 + 1,28 x 7,56 = 57,68.
Второй метод дает более узкий прогнозный интервал.