Решение краевой задачи

Вид материала

Решение

Содержание При использовании метода сеток надо выполнить следующие четыре этапа 2) заменить дифференциальный оператор некоторым разно­стным оператором Рис. ?. Узлы равномерной разностной сетки ВС = , тогда Практическая часть Значения у в граничных узлах сетки явно заданы у(?)=?, у(2)=2. Матрица системы изготавливалась в Excel, там же система решалась вычислением обратной матрицы и умножением ее на столбец правой В практических задачах непростым вопросом иногда является выбор сетки (в простейшем случае равномерной сетки – выбор числа узлов

Подобный материал:

• Пояснительная записка к курсовому проекту на тему «Решение краевой задачи для системы, 80.38kb.
• Задачи продолжения температурных полей по данным точечных измерений А. Н. Васильев, 73.76kb.
• Решение краевой задачи для уравнения состоит в определении значений функции y(X), удовлетворяющей, 28kb.
• Положение о II краевой олимпиаде по истории «Россия и мир», 374.02kb.
• Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения, 49.69kb.
• Решение о реструктуризации задолженности по отмененным налогам и сборам в части средств,, 80.13kb.
• Языки программирования, 27.65kb.
• Курсовой проект по дисциплине «Теория информационных процессов и систем» тема: Задачи, 258.87kb.
• На конкурс участники представляют материалы, отражающие формы и методы воспитания детей, 40.49kb.
• Решение задачи одним из математических методов, 440.71kb.

Курсовая работа по теме:

Решение краевой задачи

Теорeтическая часть:

Решение краевой задачи методом конечных разностей


Основные понятия и определения метода конечных разностей

Метод конечных разностей является мощным аппаратом вы­числительной математики, с помощью которого решаются разно­образные задачи из различных областей науки. Метод конечных разностей называется также методом сеток. Он используется при решении краевых задач для обыкновенных дифференциальных урав­нений и для уравнений в частных производных.

При использовании метода сеток надо выполнить следующие четыре этапа:

?) заменить область непрерывного изменения аргумента обла­стью дискретного его изменения;

2) заменить дифференциальный оператор некоторым разно­стным оператором;

3) сформулировать разностный аналог для граничных условий;

4) решить полученную в результате осуществления первых трех этапов алгебраическую систему конечно-разностных уравнений.

Рассмотрим каждый из этапов отдельно. На первом этапе нуж­но ввести разностную сетку. Существует два вида сеток: равномер­ные и неравномерные.

Исследуем сначала простейший случай - равномерная сетка. Допустим, что требуется определить решение дифференциального уравнения на отрезке [а, b]. Выбираем произвольное число разбие­ний отрезка - п. Тогда получим (n + ?) узел разностной сетки (рис. ?).



Рис. ?. Узлы равномерной разностной сетки


Шаг сетки определяется по формуле

, (?.?)

а сами узлы вычисляются так:

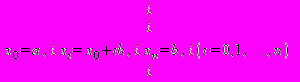(?.2)

Узлы и называются граничными узлами, а — внутренними узлами разностной сетки.

Второй этап состоит в замене производных, входящих в дан­ное дифференциальное уравнение, соответствующими конечно-раз­ностными соотношениями. Получим сначала выражение первой производной в произвольном узле . Введем обозначения

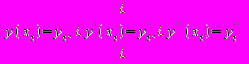(?.3)

и рассмотрим три последовательных узла сетки 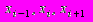, (рис. 2).

Очевидно, что в треугольнике АВС стороны АС = 2,

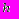ВС = , тогда .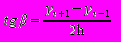

Проведем касательную ML к кривой 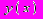в точке и обозначим через угол наклона касательной с осью абсцисс. Как известно, касательная - это предельное положение секущей АВ, когда 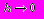,поэтому при 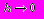∟∟. Согласно геометрическому смыслу производной имеем . Сравнивая выражения и , получим аппроксимацию первой производной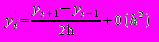

(?.4)

где - бесконечно малая порядка ,



Рис. 3.2. Выражение производной с помощью конечных разностей;

- середина интервала ()


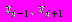Формула (?.4) определяет значение первой производной через значения функции в симметричных относительно 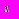. узлах и называется выражением производной через центральные разности. Для вывода формулы второй производной в разностном виде воспользуемся тем, что 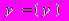а первую производную запишем по формуле (?.4) в промежуточных узлах 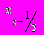и :

.

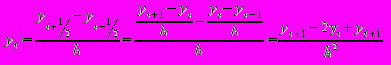Окончательно получим следующее выражение второй произ­водной

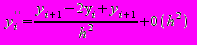(?.5)

Формула (?.5) определяет значение второй производной че­рез значения функции в трех последовательных узлах разностной сетки. Аналогичным образом получаются и выражения для третьей и четвертой производных

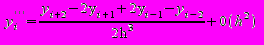, (?.6)

.


Краевая задача для линейных дифференциальных уравнений

Рассмотрим линейное дифференциальное уравнение второго порядка

y'' + p(x) y' + q(x) y = r(x), (?)

y’’-2xy’+xy=x²-?

где p(x), q(x), r(x) – заданные функции.

В нашем случае: p(x)=-2x; q(x)=x; r(x)=x²-?.

Требуется решить краевую задачу

y(a) = y_a , y(b) = y_b .

в нашем случае y(?)=?; y(?)=3

Разобьем интервал [a,b] на n равных частей и введем разностную сетку по формулам :

x_? = a, x_? = x_? + ih , x_n = b, (i+?,?,…,n)

Обозначим значения коэффициентов уравнения (?) в узлах разностной сетки следующим образом:

p(x_i) = p_i , q(x_i) = q_i , r(x_i) = r_i . (2)

Возьмем первый внутренний узел сетки x_i и заменим первую и вторую производные по формулам

y'_i = (y_i+? – y_i-?)/2h + ?(h²),

y''_I = (y_i+? – 2y_i + y_i-?)/h² + ?(h²),

где ?(h²) – бесконечно малая порядка h².

Тогда в точке x_? получим следующее разностное уравнение:

(y₂ – 2y_? + y_?)/ h² + p_?(y₂ – y_?)/2h + q_?y_? = r_? , (3)

Это уравнение аппроксимирует уравнение (?) с точностью до бесконечно малой ?(h²). Преобразуем уравнение (3) к виду

-с_?y_? + b_?y_? = f_?,

a_?y_? - c_?y_? + b_?y₂ = f_?,

a₂y_? – c₂y₂ + b₂y₃ = f₂,

………………………… (4)

a_iy_i-? – c_iy_i + b_iy_i+? = f_i,

…………………

a_n-?y_n-2 – c_n-?y_n-? + b_n-?y_n = f_n-?,

a_ny_n-? – c_ny_n = f_n.

Для этого умножим все слагаемые уравнения (3) на h² и приведем подобные члены:

(? – p_?h/2) y_? – (2 - q_?h²) y_? + (? + p_?h/2) y₂ = r_?h² . (5)

Сравнивая (5) и (4), получим

a_? = ? – p_?h/2; c_? = 2 - q_?h²; b_? = ? + p_?h/2; f_? = r_?h².

Запишем уравнение (?) в точке x₂:

(y₃ – 2y₂ + y_?)/ h² + p₂(y₃ – y_?)/2h + q₂y₂ = r₂ ,

и преобразуем к виду (4):

(? – p₂h/2) y_? – (2 – q₂h²) y₂ + (? + p₂h/2) y₃ = r₂h² ,

откуда следует, что

a₂ = ? – p₂h/2; c₂ = 2 – q₂h²; b₂ = ? + p₂h/2; f₂ = r₂h².

Аналогичным образом для произвольного внутреннего узла x_i (I =?,2,…,n-?) имеем


(y_i+? – 2y_i + y_i-?)/ h² + p_i(y_i+? – y_i-?)/2h + q_iy_i = r_i ,

a_iy_i-? - c_iy_i + b_iy_i+? = f_i , (6)

a_i = ? – p_ih/2; c_i = 2 – q_ih²; b_i = ? + p_ih/2; f_i = r_ih². (8)

Записав уравнение (6) для всех внутренних узлов сетки, получим систему линейных алгебраических уравнений, состоящую из (n-?) уравнений и содержащую (n+?) неизвестных (y_?, y_?,…, y_n). Недостающие два уравнения получим из краевых условий (2). Окончательно полная конечно-разностная система уравнений примет вид

y_? = y_a,

a_?y_? - c_?y_? + b_?y₂ = f_?,

a₂y_? – c₂y₂ + b₂y₃ = f₂,

………………………… (7)

a_iy_i-? – c_iy_i + b_iy_i+? = f_i,

…………………

y_n = y_b.

Система уравнений (7) представляет собой систему линейных алгебраических уравнений с трехдиагональной матрицей (4) и легко решается методом прогонки. В результате решения получим дискретные значения y_i в узлах разностной сетки.


ПРАКТИЧЕСКАЯ ЧАСТЬ:


Решить краевую задачу для линейного дифференциального уравнения 2-го порядка:

с краевыми условиями

у(?)=?, у(2)=2.


Решение:


В условии не указаны никакие требования к погрешности, равно как и не предписан определенный метод решения. Будем решать задачу методом конечных разностей на сетке из ?? узлов на интервале от ? до 2.

Значения у в граничных узлах сетки явно заданы у(?)=?, у(2)=2.

Система уравнений для 9 внутренних узлов получается при замене дифференциального уравнения разностным.

Производные аппроксимируются симметричными разностями



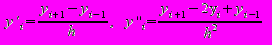
где h – шаг сетки ( в нашем случае h=?,?).


Уравнение для внутреннего узла после приведения подобных членов имеет вид




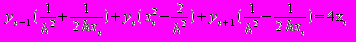
Матрица системы и столбец правой части

?											?
??4.545	-?98.79	95.45455									4.4
	??4.?667	-?98.56	95.83333								4.8
		??3.8462	-?98.3?	96.?5385							5.2
			??3.57?4	-?98.?4	96.42857						5.6
				??3.3333	-?97.75	96.66667					6
					??3.?25	-?97.44	96.875				6.4
						??2.94?2	-?97.??	97.?5882			6.8
							??2.7778	-?96.76	97.22222		7.2
								??2.63?6	-?96.39	97.36842	7.6
										?	2

Матрица системы изготавливалась в Excel, там же система решалась вычислением обратной матрицы и умножением ее на столбец правой части.


Ответ:

x	y
?	0?.??.?2
?.?	-?.?53?735?9
?.2	-?.?6443365
?.3	-?.?25726476
?.4	?.?7?6?944
?.5	?.23?72?22?
?.6	?.45857?879
?.7	?.755?7??28
?.8	?.??7??5586
?.9	?.536677929
2	2

Замечание?. В учебном примере, где число узлов сетки мало, а погрешность решения не задана в условиях задачи, удалось решить систему алгебраических уравнений просто обращением матрицы.

В практических задачах, где число узлов сетки велико настолько, что обратить матрицу такого размера с требуемой точностью не удается вследствие накоплениявычислительных погрешностей, приходитмся применять итерационное уточнение решения линейной системы.


Замечание2. В практических задачах непростым вопросом иногда является выбор сетки (в простейшем случае равномерной сетки – выбор числа узлов).

Иногда удается разумно оценить расстояние между узлами из физических соображений, иногда приходится применять процедуру, аналогичную процедуре двойного счета при численном интегрировании: постепенное дробление ячеек сетки до долстижения сходимости в себе последовательности решений на разных сетках. При этом при дроблении сетки предыдущее решение, распространенное на новую сетку линейной интерполяцией между узлами старой сетки, является начальным приближением для построения решения на новой сетке.