Решение краевой задачи для уравнения состоит в определении значений функции y(X), удовлетворяющей данному уравнению краевым условиям
| Вид материала | Решение |
СодержаниеY=Y(x) выше указанного уравнения на отрезке [a,b] Методы конечных разностей |
- Назначение программы. Данная программа предназначена для исследования функции. Всостав, 270.6kb.
- Метод прогонки решения краевой задачи для обыкновенного дифференциального уравнения, 49.69kb.
- Методы решения тригонометрических уравнений, 53.9kb.
- Вывод трехмерного уравнения теплопроводности. Постановка граничных задач, 20.07kb.
- Численное решение обыкновенных дифференциальных уравнений, 10.66kb.
- Пояснительная записка к курсовому проекту на тему «Решение краевой задачи для системы, 80.38kb.
- Синявская средняя общеобразовательная школа, 63.47kb.
- Задача Коши для неоднородного уравнения с однородными граничными условиями, 80.58kb.
- Тема: Уравнение с двумя переменными. Цели урока, 251.03kb.
- Положение Окраевом слете ученических производственных бригад I. Цели и задачи проведения, 1013.21kb.
Практическое занятие №8
Краевые задачи ОДУ. Метод конечных разностей
На предыдущем занятии рассматривались задачи с начальными условиями, т.е. с условиями в одной точке x=x0. На практике приходится часто решать другого типа задачи, когда условия задаются при двух значениях независимой переменной (на концах рассматриваемого отрезка). Такие задачи, называемые краевыми, получаются при решении уравнений высших порядков или систем уравнений.
Краевая задача состоит в отыскании решения Y=Y(x) выше указанного уравнения на отрезке [a,b], удовлетворяющего на концах отрезка условиям Y(a)=A, Y(b)=B.
Граничные условия могут быть заданы не только в частном виде, но и в более общем виде:
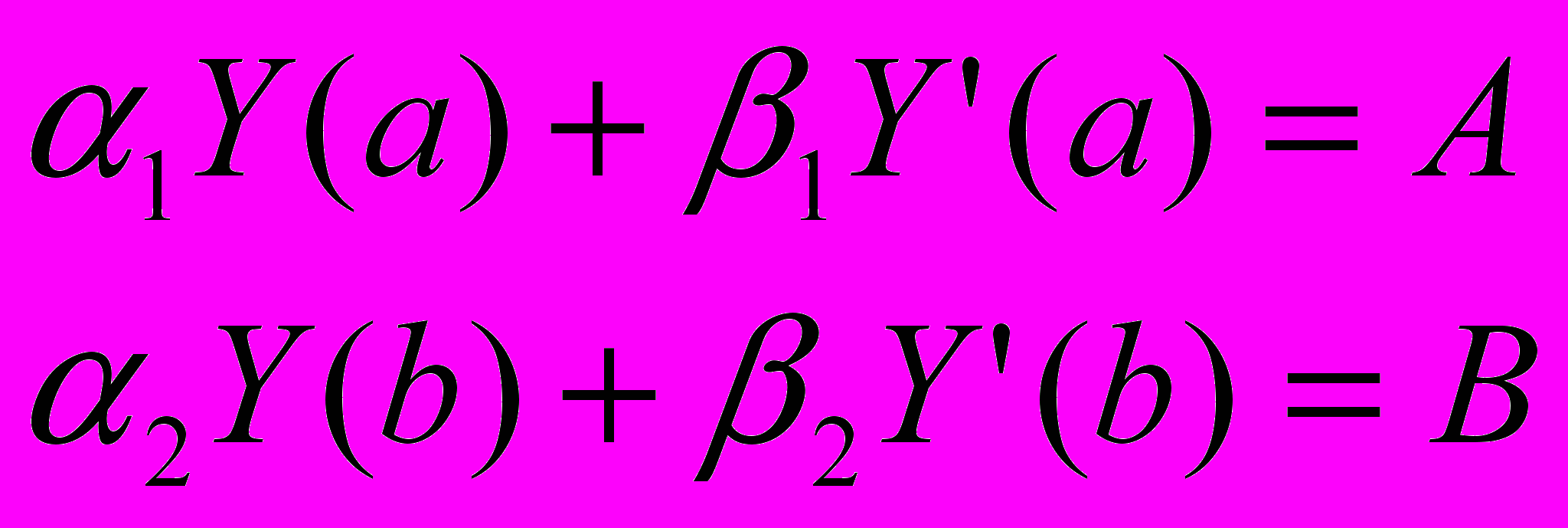 .
.К основным численным методам решения краевых задач относятся метод стрельбы и методы конечных разностей.
Методы конечных разностей
Решение краевой задачи для уравнения
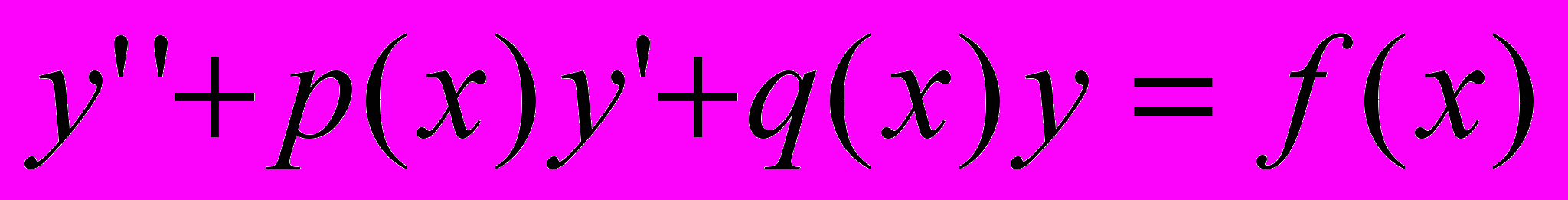 состоит в определении значений функции y(x), удовлетворяющей данному уравнению краевым условиям
состоит в определении значений функции y(x), удовлетворяющей данному уравнению краевым условиям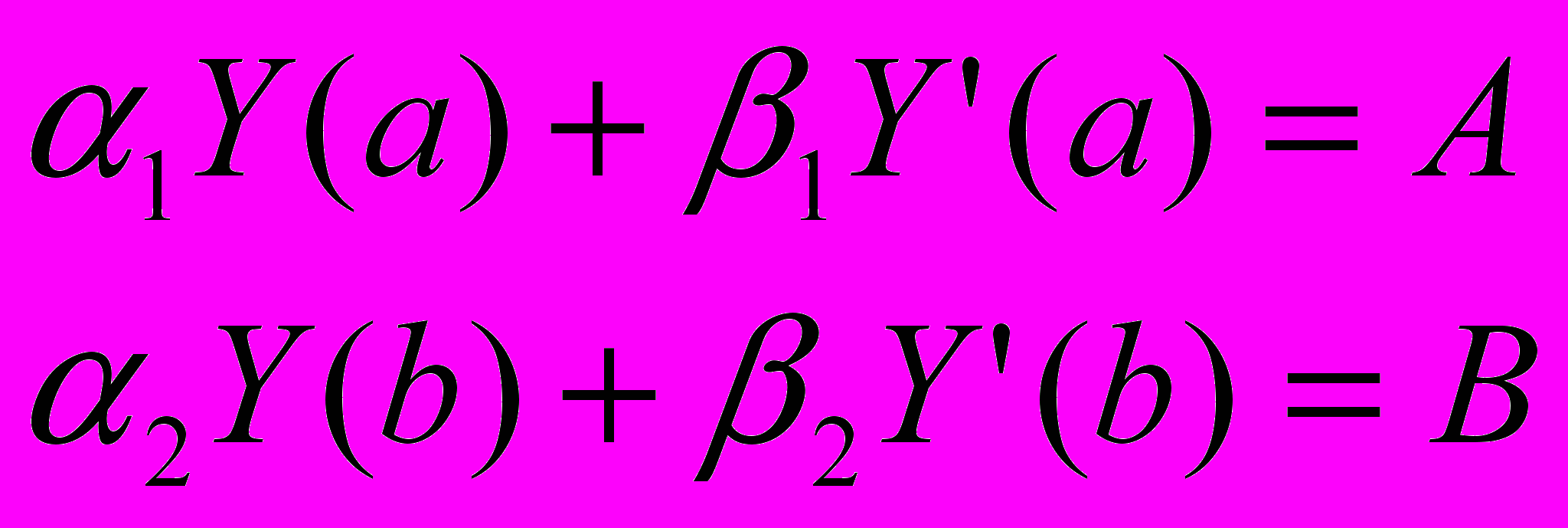 .
.Разбив отрезок [a,b] на n равных частей с шагом h=(b-a)/n, получают точки xi=a+ih, в которых требуется найти искомые значения yi=y(xi).
Производные заменяют их конечно-разностными аппроксимациями:
Для внутренних точек (i=1, 2,.., n-1):
 .
.Для граничных точек x0=a и xn=b выполняются равенства
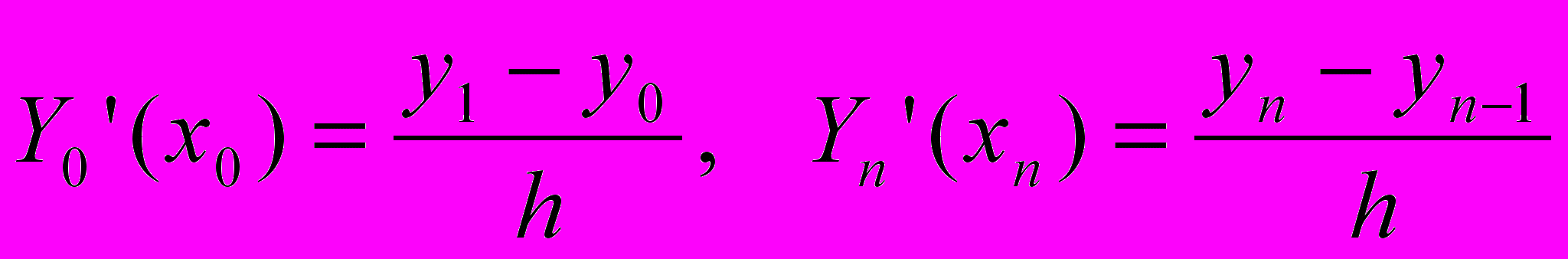 или
или  .
.В результате получается система уравнений с неизвестными y0, y1, …, yn. Решив эту систему получают таблицу приближенных значений искомой функции.
Пример 1
Используя метод конечных разностей, составить решение краевой задачи для ОДУ.
 .
.Решение.Разбив отрезок [2; 2.3] на части шагом h=0.1, получим 4 узловые точки x0=2, x1=2.1, x2=2.02, x3=2.3. Две точки x0 и x3 являются граничными, а две другие – внутренними.
Данное уравнение во внутренних точках заменим конечно-разностным уравнением:

 (i=1, 2).
(i=1, 2).Из краевых условий составим конечно-разностные уравнения в конечных точках:
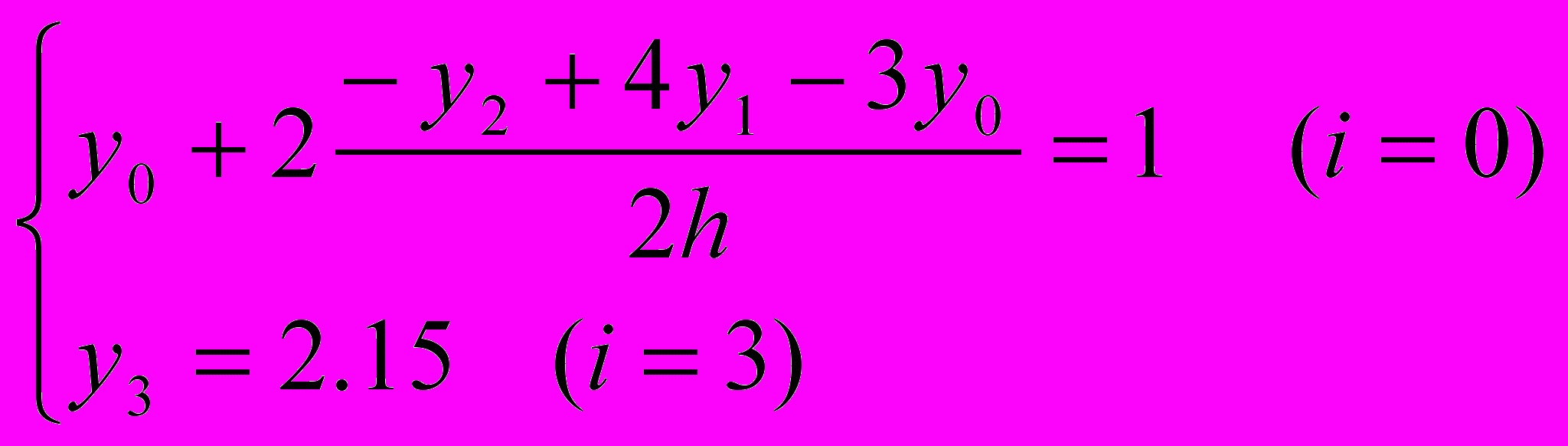 .
.Данная задача сводится к решению системы уравнений
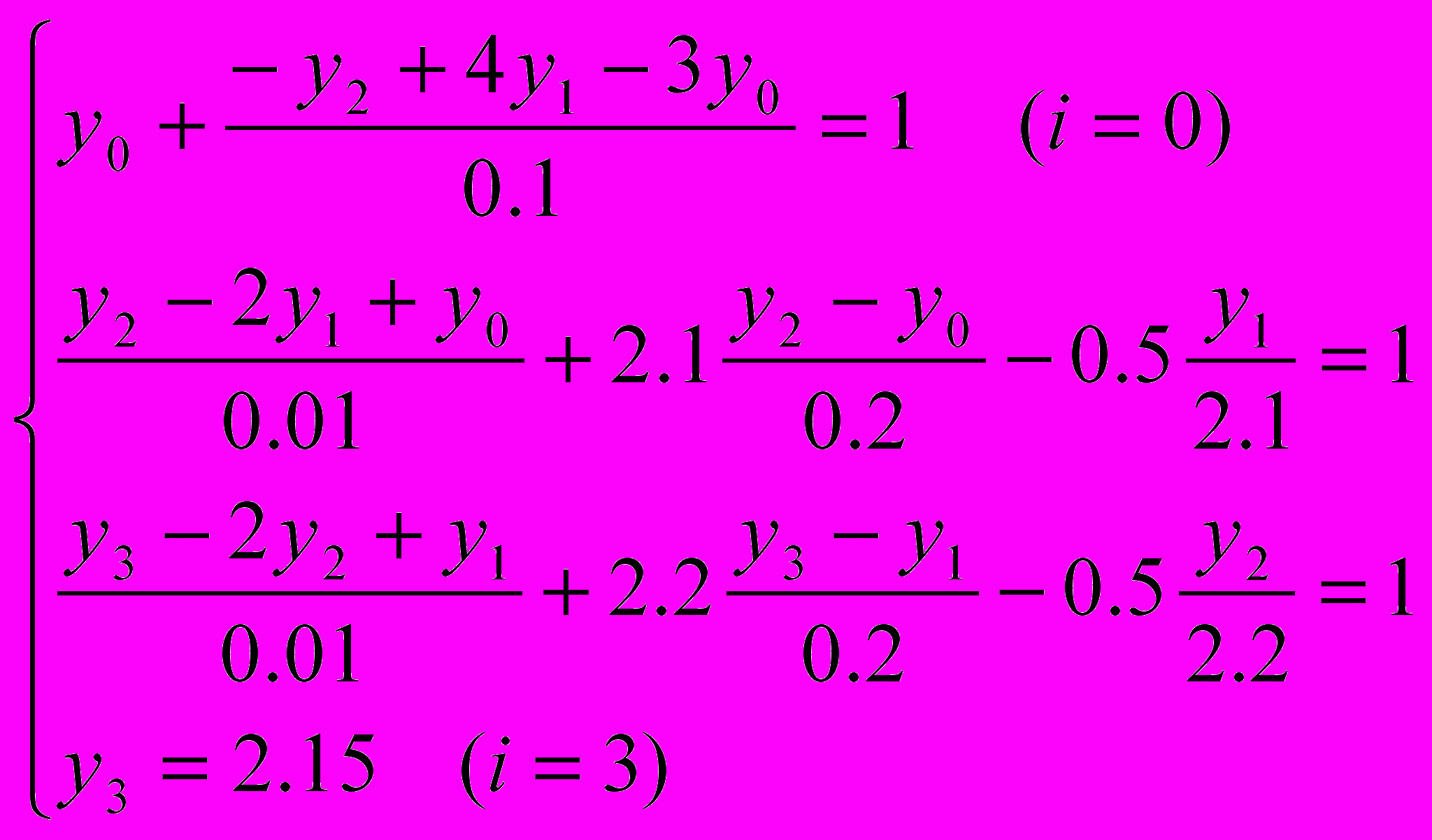
Выполнив преобразования, имеем
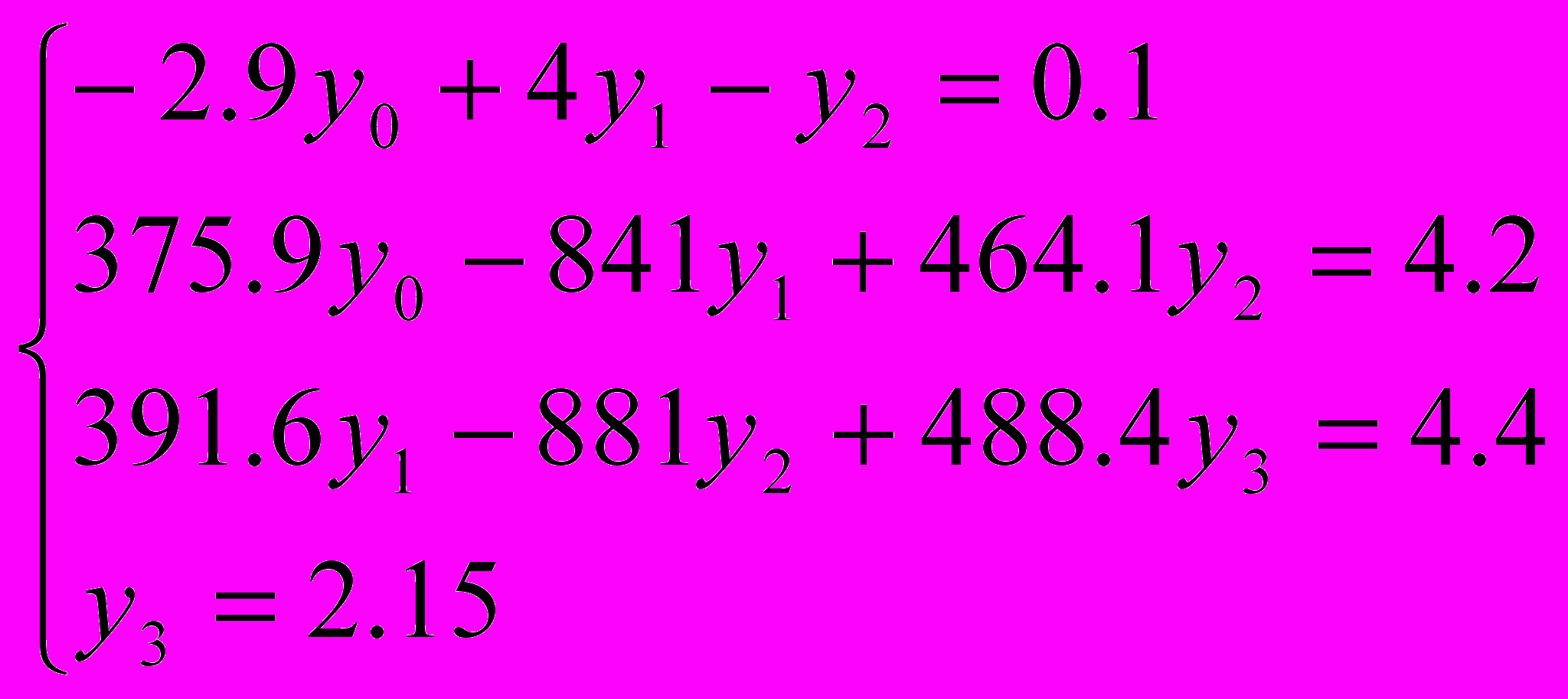 .
.Подставим y3 в третье уравнение:
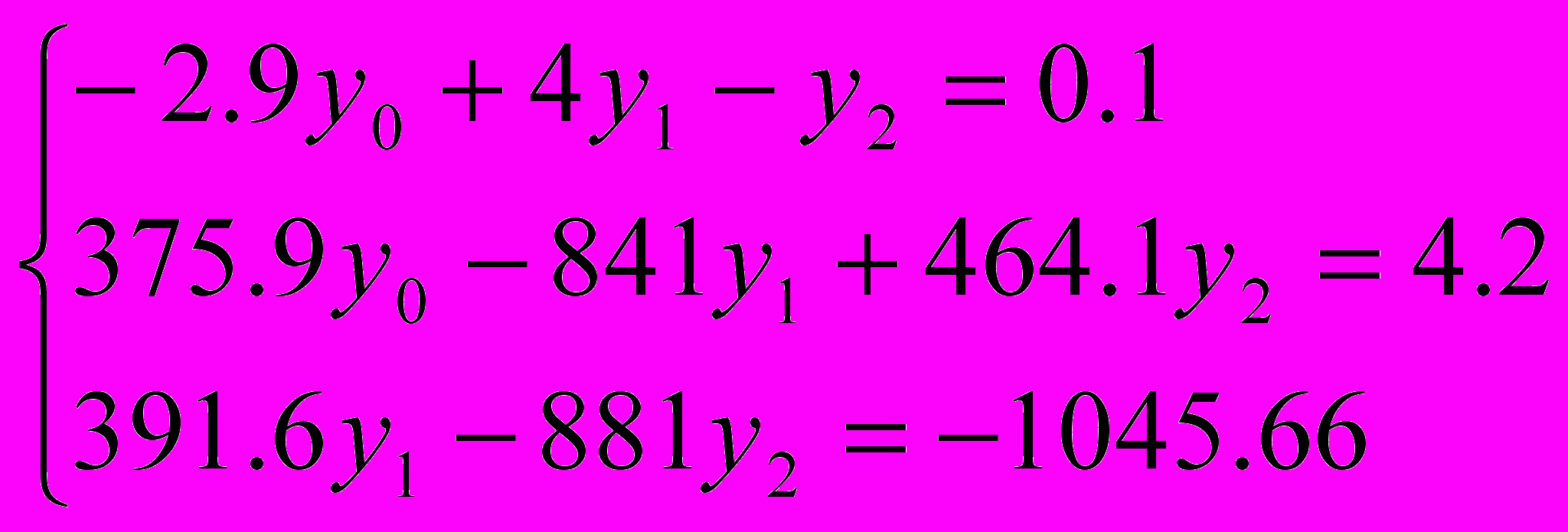
| x | y |
| 2.0 | 2.235 |
| 2.1 | 2.185 |
| 2.2 | 2.158 |
| 2.3 | 2.150 |
Ответ:
Задачи для самостоятельного решения:
Задача 1
Используя метод конечных разностей, составить решение краевой задачи для ОДУ.
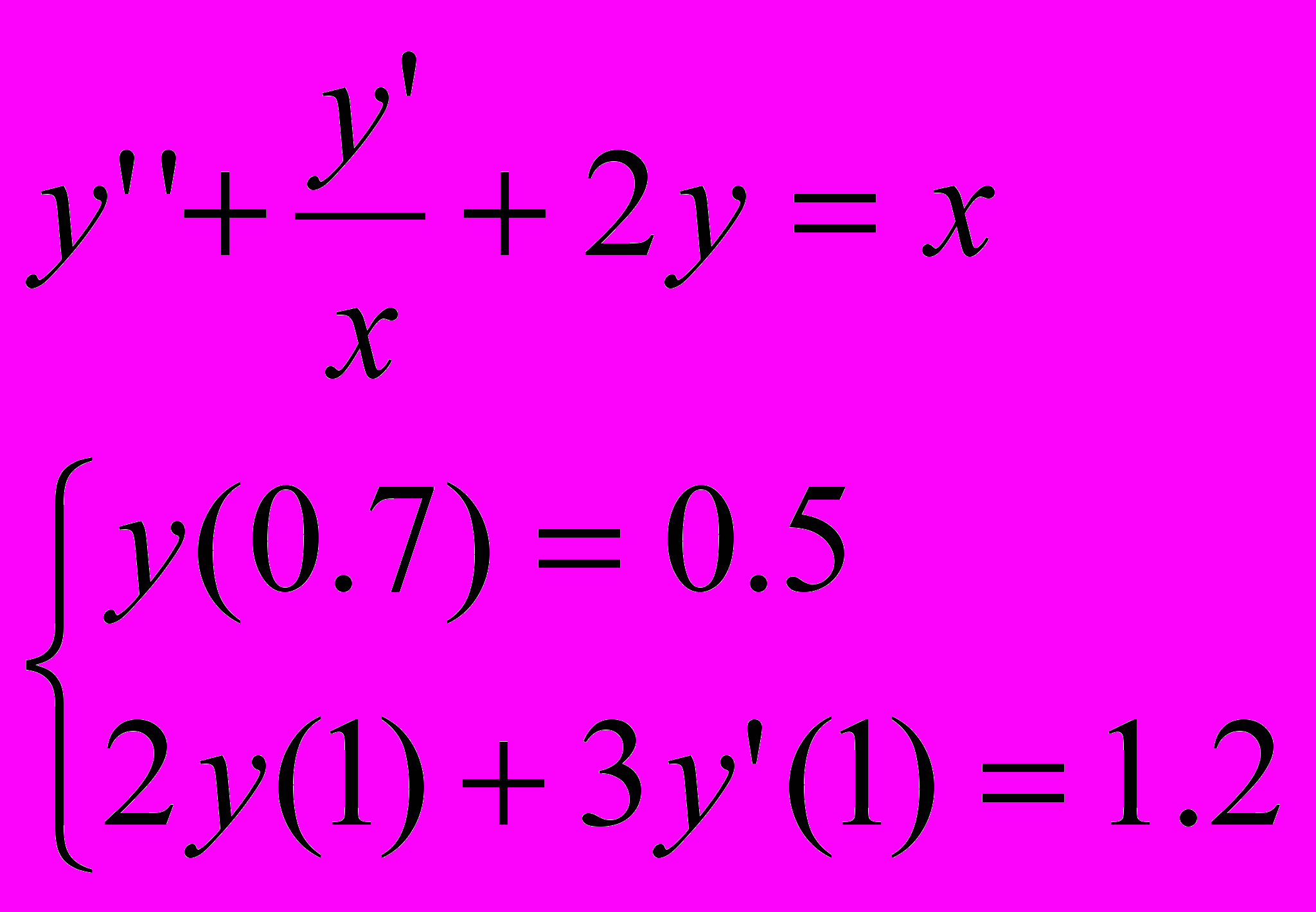
Задача 2
Используя метод конечных разностей, составить решение краевой задачи для ОДУ.
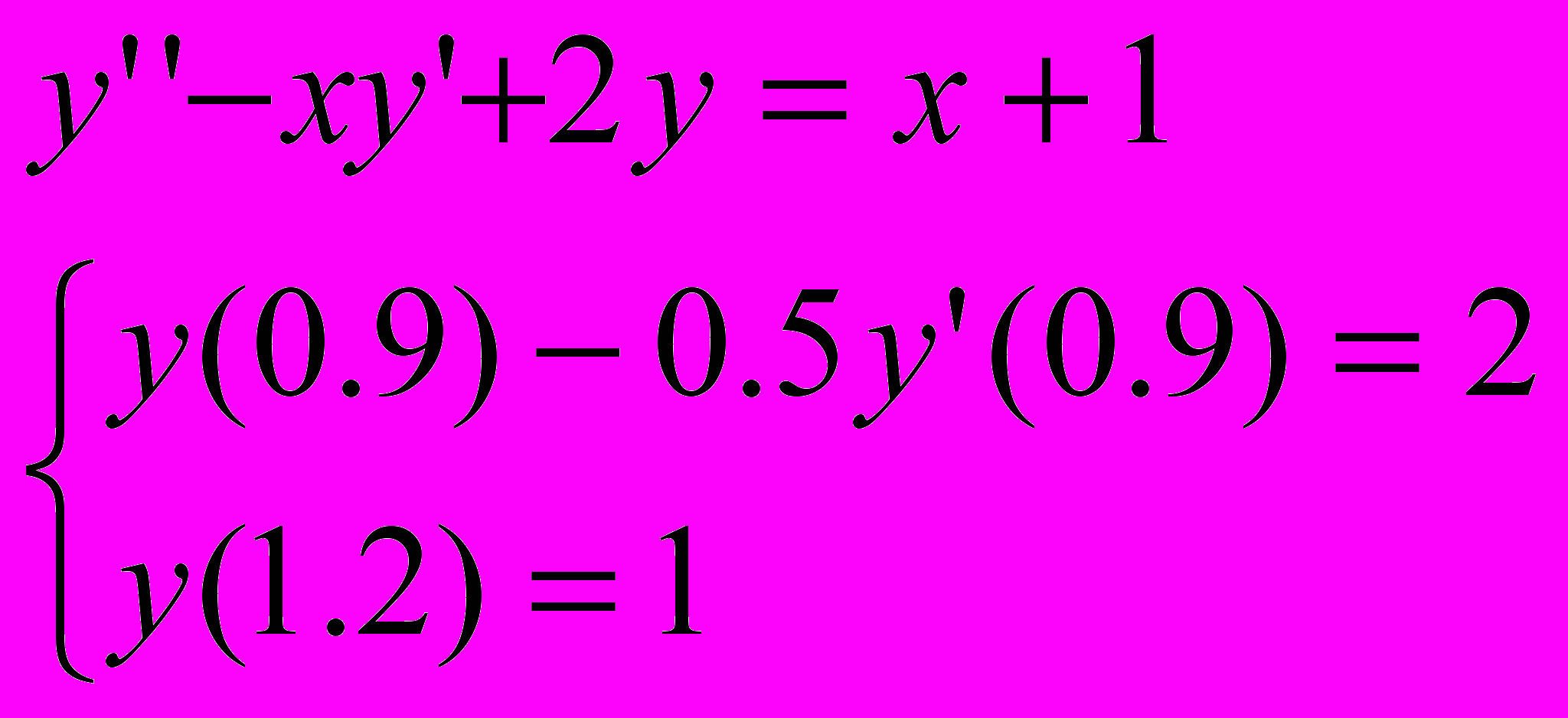 .
.