Решение задачи одним из математических методов

Вид материала

Решение

Содержание Этапы линейного программирования Метод Гаусса. Операции над матрицами. Ранг матрицы 6. Неопределенная система ЛАУ. Базисные. 7. Множества. Выпуклые линейные комбинации. 8. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек. 9. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым. 10. Теорема об экстремальном значении целевой функции. 13. Нахождение исходного опорного решения. 14. Симплексный метод. 16. Приращение целевой функции 17, 18. Критерии оптимальности 19. Метод невязок. 20. Двойственные задачи. Исх. задача Если задачи симметричны Теоремы двойственности. 26-27. Теорема о разрешимости транспортной задачи. Доказательство ограниченности функции на множестве планов транспортной задачи 28. Теорема о ранге матрицы коэффициентов ТЗ ... Полное содержание

Подобный материал:

• Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 25.18kb.
• Задачи линейного программирования и задачи математической экономики Методика преподавания, 19.49kb.
• Бравый Евгений Ильич, 55.95kb.
• Тематический план учебной дисциплины, 52.63kb.
• Анализ методик использования моделирования в процессе обучения дошкольников математике, 472.24kb.
• Одним из эффективных математических методов для определения зависимости по множеству, 139.29kb.
• Д э. н. М. В. Грачева, зав кафедрой «Математических методов анализа экономики», 20.32kb.
• Задачи внеклассного занятия: Рассмотреть практическое применение математических знаний, 95.15kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 24.5kb.

1. Предмет и задачи курса. Экономико-математическая модель задачи линейного программирования. Пример.

Математическое программирование – дисциплина, занимающаяся изучением экстремальных задач (max/min), разработкой методов их решения.

Математическое программирование делится на задачи линейного и нелинейного программирования (целочисленное, выпуклое, динамическое, параметрическое). Многие инженерно-экономические задачи можно с достаточной степенью точности описать с помощью линейной целевой функции и системы линейных ограничений. Раздел, изучающий такие задачи, называется линейным программированием.

Этапы линейного программирования:

1. постановка задачи (словесная формулировка), формулировка условий задачи, выбор критериев оптимальность
   
2. сбор необходимых данных, составление исходной матрицы
   
3. построение экономико-математической модели
   
4. решение задачи одним из математических методов
   
5. анализ полученных результатов
   

Экономико-математическая модель.

Для производства 3 видов изделий (A,B,C) используется 3 вида различного сырья в количестве 180, 210, 244 единицы. Нормы затрат каждого вида сырья на производство единицы продукции данного вида приведены в таблице:

I	4	2	1
II	3	1	3
III	1	2	5

Цена от реализации изделий:

A	B	C
10	14	12

Определить план выпуска продукции, при котором прибыль максимальна. Составить математическую модель.

Решение: пусть предприятие производит x₁ изделий вида А, x₂ изделий вида B и x₃ изделий вида С. Так как производство ограничено имеющимся сырьем и количеством изготовляемых изделий, то должны выписываться условия:

4х₁+2х₂+х₃

3х₁+х₂+3х₃

х₁+2х₂+5х₃

все x0,

Z = 10x1+14x2+12x3 (max).

Методы решения:

1. графический (быстро и наглядно решает простейшие задачи)
   
2. симплекс-метод (универсальный метод)
   
3. метод потенциалов (им решаются транспортные задачи)
   

Необходим контроль, анализ решений, корректировка оптимального плана.

2. Общая постановка задачи линейного программирования. Каноническая форма задачи линейного программирования.

Найти совокупность значений x₁, x₂, … , x_n, удовлетворяющим условию и доставляющим функции Z экстремальное значение.

n

∑aijxj (<=, =>,=)bi - ограничения (1,1)

i=1

xj=>0 - условия неотрицательности (1,2)

i=1,m

j=1,n


n

Z = ∑cjxj - целевая функция (1,3)

i=1

Совокупность значений переменных x₁, x₂, … , x_n, удовлетворяющих условиям 1.1-1.3 называется допустимым планом. Оптимальным планом называется такое решение, при котором целевая функции достигает экстремума.

Канонический вид задачи линейного програмирования:

а₁₁х₁+ а₁₂х₂+ …+а_1jх_j+..+a_1nx_n=b₁

а₂₁х₁+ а₂₂х₂+…+ а_2jх_j+..+a_2nx_n=b₂

а_i1х₁+ а_i2х₂+…+ а_ijх_j+..+a_inx_n=b_i

а_m1х₁+ а_m2х₂+…+ а_mjх_j+..+a_mnx_n=b_m

все x_i =>0, i=1,n j=1,m

Z=c₁x₁+c₂x₂+…+c_nx_n (max)

Приведение задачи к каноническому виду:

1. переход от ограничений-неравенств к ограничениям-равенствам (ограничение-неравенство вида  сводится к ограничению-равенству добавлением к его левой части дополнительной (балансовой) неотрицательной переменной, а вида  - вычитанием)
   
2. замена переменных, которые не подчинены условию неотрицательности
   
3. переход задачи min к max (Z = Z)
   

3. Система линейных алгебраических уравнений (СЛАУ). Метод Гаусса. Пример.

Система м линейных уравнений с н переменными имеет вид:

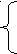а11х1+ а12х2+ …+а1jхj+..+a1nxn=b1

а21х1+ а22х2+…+ а2jхj+..+a2nxn=b2

аi1х1+ аi2х2+…+ аijхj+..+ainxn=bi

аm1х1+ аm2х2+…+ аmjхj+..+amnxn=bm

где аij, bi (i=1,n j=1,m) - произвольные числа при переменных, называемые коэффициентами при переменных и свободныи членами уравнений.

В более краткой записи с помощью знаков суммирования систему можно записать:

n

∑aijxj =bi

j=1

Решение такой системы – это набор чисел, при подстановке которых в эту систему каждое уравнение превращается в тождество. Совместной СЛАУ называется такая система, которая имеет хотя бы одно решение. Если система решений не имеет, то она называется несовместной.

Метод Гаусса.

Метод последовательного исключения переменных заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Ход решения

1. умножая 1-ое уравнение на подходящие числа и прбавляя полученные уравнения соответственно ко второму, третьему ,… m-му уравнению системы, исключим переменную х₁ из всех последующих уравнений, начиная со второго.
   

П
редположим что а₂₂ <>0 умножая второе уравнение на подходящие числа и прибавляя полученные уравнения соответственно к третьему, четвертому,…, m-му уравнению системы, исключим переменную х₂ из всех последующих уравнений, начиная с третьего.

4. Матрицы.

Матрицей размера м*н называется прямоугольная таблица чисел, содержащая м строк и н столбцов. Числа составляющие матрицу называются ее элементами.

Матрица состоящая из одной строки, называется матрицей (вектором) – строк, а из одного столбца – матрицей –столбцом

Матрица называется квадратной, если число ее строк = числу ее столбцов. Элементы матрицы, у которых номера столбца = номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Если все недиоганальные элементы квадратной матрицы =0, то матрица назыв диагональной. Если у диагональной матрицы все диагональные элементы = 1, то матрица назыв единичной матрицей. Матрица любого порядка назыв нулевой, если все ее эл-ты = 0

Операции над матрицами.

1. Умножение матрицы на число. Все эл-ты матрицы умножаем на это число. Произведением матрицы А на число № назыв матрица В=№А.
   
2. Сложение матриц. Сумма 2х матриц одинакового размера назыв матрица С=А+В, эл-ты которой cij=aij+bij
   
3. Вычитание. А-В=А+(-1)*В
   
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов 1ой матрицы =числу строк второй. Тогда произведением матриц А*В назыв такая матрица С, каждый элемент которой сij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
   
5. Транспонирование. Переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка.
   
6. Возведение в степень. Целой положительной степенью А в степени м (м>1)квадратной матрицы А называется произведение м матриц, равных А.
   

В матрице А размера m x n вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где k≤min(m;n). Определители таких подматриц называются минорами k-го порядка матрицы А.

Ранг матрицы – наивысший порядок отличных от нуля миноров матрицы.


5. Обратная матрица.

Матрица А(-1) называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица.

Теорема: Обратная матрица А(-1)существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Необходимость. Пусть матрица А имеет обратную А (-1), т.е. А*А (-1)= А(-1)А=Е. Тогда по свойству определителя (определитель произведения двух квадратных матриц равен произведению их определителей) │А*А(-1)│= │А│*│А(-1)│= │Е│=1, т.е. │А│=/0 и │A(-1) =/ 0

Достаточность. Пусть │А│=/ 0.Рассмотрим квадратную матрицу n-ого порядка Ẫ, называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы А’, транспонированной к А: ẫij= А’ij=Aji (i=1,n; j=1,n) тогда элементы произведения матриц Ẫ*А=В определяются по правилу умножения матриц: bij = s=1∑n ẫisasj = s=1∑n Asi asj =

|A| i=j

0 при i=/j

Поэтому матрица В является диагональной, элементы ее главной диагонали = определителю исходной матрицы. Аналогично доказывается, что произведение А на Ẫ равно той же матрице В:А* Ẫ= Ẫ*А=В. Отсюда следует, что если в качестве обратной матрицы взять матрицу А(-1)= 1/ │А│* Ẫ (│А│<>0) (1)

То произведение А(-1) *А и А*А(-1) равны единичной матрице Е n-ого порядка: А(-1)*А=А*А(-1)= 1/│А│*В=Е

Алгоритм вычисления:

1. находим определитель исходной матрицы. Если │А│=0, то матрица А – вырожденная и обратной матрицы не существует. Если │А│<>0, то матрица А – невырожденная и обратная матрица существует.
   
2. Находим матрицу А’, транспонированную к А
   
3. Находим алгебраическое дополнение элементов транспонированной матрицы А’ij=Aij (i=1,n; j=1,n) и составляем из них присоединенную матрицу Ẫ: ẫij= А’ij= Аij
   
4. Вычисляем обратную матрицу по формуле (1,14)
   
5. Проверяем правильность вычисления обратной матрицы А(-1), исходя из ее определения А*А (-1)= =А(-1)А=Е
   

6. Неопределенная система ЛАУ. Базисные.

Неопределённая система линейных алгебраических уравнений имеет бесчисленное множество решений. Придав свободным неизвестным нулевое значение получим решение системы, которое называется базисом.

Если система приведена к единичному базису, то её базисное решение находится сразу. Для этого необходимо положить свободные неизвестные равными нулю, тогда свободные члены определят значения базисных неизвестных.

Чтобы найти все базисные решения системы не возвращаясь вновь к исходной системе, используют преобразование однократного перемещения, основанном на методе Ж. Гаусса.

В любом единичном столбце выбирают отличное от нуля число и выполняют 1 итерацию этого метода, при этом необходимо следить, чтобы преобразования не повторялись.

Число базисных решений не должно превышать число С

Сrn=n!/r!(n-r)!

N – количество неизвестных в системе.

R – ранг матрицы (кол-во уравнений в системе)


7. Множества. Выпуклые линейные комбинации.

Пусть на плоскости х10х2 заданы две точки А1(х’1х’2) и А2(х’’1х’’2), определяющие направленный отрезок А1А2. Выразим координаты произвольной внутренней точки через координаты его концов, векторы А1А и А1А2 параллельны и одинаково направленные: А1А = t(А1А2), 0<=t<=1

A1A2=(x1-x’1;x2-x’2), A1A2=(x’’1-x’1;x’’2-x’2), x1-x’1=t(x’’1-x’1), x2-x’2=t(x’’2-x’2)

x1=(1-t)x’1+tx’’1, 1-t=λ1, t= λ2

x1= λ1x’1+ λ2x’’1, x2= λ1x’2+ λ2x’’2

λ1≥0 λ2≥0, λ1+ λ2=1

учитывая, что координаты точки А являются суммами одноимённых координат точек А1 и А2, умноженных соответственно на числа λ1 и λ 2, окончательно получаем:

А= λ1А1+ λ2А2, λ 1<=0, λ2≥0, λ1+λ2=1

Точка А, для которой выполняются эти условия называется выпуклой линейной комбинацией точек А1 и А2.

При условии λ1=1 и λ2=0 точка А совпадает с началом отрезка А1, λ1=0 λ2=1 – с концом

Таким образом если t пробегает все значения от 0 до1 то точка А описывает отрезок А1А2. Точки А1 и А2 называют угловыми или крайними точками отрезка А1А2. Из определения линейной выпуклой комбинации точек очевидно что угловая точка не может быть представлена как выпуклая линейная комбинация 2 других точек отрезка.

Множество называется выпуклым, если вместе с любыми 2 своими точками оно содержит и их произвольную линейную выпуклую комбинацию.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь 2 других различных точек данного множества.


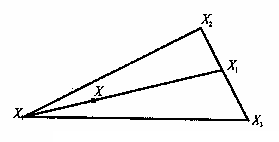
8. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек.

Доказательство. Возьмем для простоты n=2, а в качестве многоугольника – треугольник X1X2X3. Через произвольную точку Х треугольника проведем отрезок Х1Х4. Поскольку точка Х лежит на этом отрезке, то Х=α1Х1 + α4Х4, где α1≥0, α2≥0, α1+α4=1.

Точка Х4 лежит на отрезке Х2Х3, следовательно, Х4= α2Х2+ α3Х3, где α2≥0, α3≥0, α2+α3=1. Подставив значение Х4 в выражение для Х, получим Х= α1Х1 + α4(α2Х2+ α3Х3)= α1Х1 + α2 α4Х2 + α3α4Х3.

Обозначив t1= α1, t2= α2α4, t3= α3α4, получим окончательно X=t1X1+t2X2+t3X3, где t1≥0, t2≥0, t3≥0 и t1+t2+t3=1.

Таким образом, точка Х есть выпуклая линейная комбинация угловых точек треугольника Х1Х2Х3.




9. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Доказательство. Пусть Х1=(х1(1), х2(1),…,xn(1)) и X2=(x1(2), x2(2),…,xn(2) – два допустимых решения задачи, заданной в матричной форме. Тогда АХ1=В и АХ2=В. Рассмотрим выпуклую линейную комбинацию решений Х1 и Х2, т.е. Х=α1Х1 + α2Х2 при α1≥0, α2≥0 и α1 + α2 =1, и покажем, что она также является решением системы. В самом деле, АХ = А(α1Х1 + α2Х2) = α1АХ1 + (1- α1)АХ2 = α1В + (1- α1)В=В, т.е. решение Х удовлетворяет системе. Но так как Х1≥0, Х1≥0, α1≥0, α2≥0, то и Х ≥0, т.е решение Х удовлетворяет и условию.


10. Теорема об экстремальном значении целевой функции.

Если задача ЛП имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более, чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой комбинацией этих точек.

Доказательство. Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1, Х2, …, Хр, а оптимальное решение – через Х*. Тогда F(X*)≥F(X) для всех точек Х многогранника решений. Если Х* - угловая точка, то первая часть теоремы доказана. Предположим, что Х* не является угловой точкой , тогда на основании теоремы о выпуклом многоугольнике, являющемся выпуклой линейной комбинацией своих угловых точек, Х* можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х*= α1Х1 + α2Х2 +…+ αрХр, αj≥0, j=1,p; j=1Σn αj=1.

Так как F(X) линейная функция, получаем F(X*)=F(α1Х1 + α2Х2 +…+ αрХр)= α1F(X1) + α2F(X2) + … + αpF(Xp). (1)

В этом разложении среди значений F(xj) (j=1,p) выберем максимальное. Пусть оно соответствует угловой точке Xk (1≤k≤p); обозначим его черех М, т.е. F(Xk)=M. Заменим в выражении (1) каждое значение этим максимальным значением М. Тогда, учитывая, что αj≥0, j=1Σp αj=1, найдем F(X*)≤α1M + α2M + … + αpM= M j=1 Σp αj=M. По предположению Х* - оптимальное решение, поэтому, с одной стороны, F(X*)≥F(Xk)=М, но, с другой стороны, доказано, что F(X*)≤М, следовательно, F(X*)=М=F(Xk), где Xk – угловая точка. Итак, существует угловая точка Xk, в которой линейная функция принимает максимальное значение.

Для доказательства второй части теоремы допустим, что F(X) принимает максимальное значение более чем в одной угловой точке, например, в точках X1, X2, … Xq, где 1≤q≤p; тогда F(X1)=F(X2)=…=F(Xq)=M.

Пусть Х – выпуклая комбинация этих угловых точек, т.е Х= α1Х1 + α2Х2 +…+ αqХq, aj≥0 (j=1,q), j=1Σq aj=1. В этом случае, учитывая, что функция F(X) – линейная, получим F(X)=А(α1Х1 + α2Х2 +…+ αqХq)= α1F(X1) + α2F(X2) + … + αqF(Xq) = α1M + α2M +…+ αqM = M j=1Σq aj=M, т.е. линейная функция F принимает максимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек X1, X2,…., Xq.


13. Нахождение исходного опорного решения.

1) Фиксируют уравнение с максимальным по модулю отрицательным свободным членом.

2) Почленно вычитают фиксированное уравнение из остальных уравнений с отрицательными свободными членами.

3) Обе части фиксированного уравнения умножают на «-1».

4) Остальные уравнения системы с неотрицательными свободными членами переписывают без изменений.

Мы придем к системе, в которой все уравнения, кроме фиксированного, разрешены. Используем симплексные преобразования, причем разрешающий элемент выбираем из условия, чтобы принадлежащий ему элемент фиксированного уравнения был положительным. При этом возможны следующие случаи:

а) Все коэффициенты при неизвестных в фиксированном уравнении неположительны, т.е. опорных решений нет.

б) Разрешающий элемент оказался в фиксированном уравнении и, следовательно, после одной итерации симплексных преобразований, система будет приведена к единичному базису.

в) Разрешающий элемент не принадлежит фиксированному уравнению, тогда симплексные преобразования проводят до тех пор, пока не придут у случаю 1 или 2. При этом необходимо следить за тем, чтобы преобразования не повторялись.


14. Симплексный метод.

Симплексный метод позволяет путем ряда преобразований, состоящих в переходе от одного опорного решения к другому (причем так, что значение целевой функции все время возрастает (max) или убывает (min)), находить оптимальное решение за конечное число шагов, либо показать неразрешимость исходной задачи.

Подготовка к решению задачи симплексным методом:

1) приведение задачи к каноническому виду

2) приведение системы уравнений к единичному базису

3) нахождение исходного опорного решения

Решение симлекс-методом:

1. Найти опорный план.

2. Составить симплекс-таблицу.

3. Исходный опорный план проверить на оптимальность, в результате чего может иметь место один из 3 случаев:

а) если Δj≥0, то исходный опорный план является оптимальным.

б) если Δj<0 и все элементы соответствующего столбца ≤0, то целевая функция не огранична сверху на множестве ее плана.

в) Δj<0 и для каждого такого j по крайней мере одно aij положительное, то можно перейти от исходного опорного плана к новому опорному плану, при котором значение целевой функции возрастает.

4. Найти разрешающий столбец и разрешающую строку. Разрешающий столбец определяется наибольшей по абсолютной величине отрицательной оценкой Δj. Разрешающая строка определяется минимальным отношением свободных членов к положительным элементам разрешающего столбца.

5. Сделать соответствующие замены в столбцах Вб и Сб и проделать один шаг метода Ж. Гауса с найденный разрешающим элементом. Пересчитать элементы в строке Δ.

6. Проверить найденный опорный план на оптимальность. Если план неоптимален и необходимо пререйти к новому опорному плану, то возвращаемся к пункту 2, а в случае получения оптимального плана или усановления неразрешимости задачи решение задачи заканчивают.


16. Приращение целевой функции

Приращение – разность между последующей и предыдущей функциями

∆ = Z2 – Z1 >0

X1 Z(X1) =Z1

| | |

X2 Z(X2) =Z2

Z2=(z1aij-∆jbi) \ aij=Z1 - ∆jbi\aij

∆ = Z1 - ∆jbi/ aij – Z1 = -∆jbi/ aij > 0

∆j < 0


17, 18. Критерии оптимальности

Теорема 1: Опорный план Х*=(х1*, х2*, 0,…, 0) задачи (1) – (3) является оптимальным, если ∆j ≥0, j = 1, n.

Теорема 2: Если ∆k< 0 для некоторого j=k и среди чисел aik нет положительных (aik ≤ 0), то целевая функция (1) задачи (1) – (3) не ограничена на множестве ее планов.

Теорема 3: Если ∆k < 0 и опорный план Х задачи (1) – (3) не вырожден, но среди чисел aik есть положительные (не все aik ≤ 0), то существует опорный план Х’ такой что Z(X’) >Z(X)

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.