Geum.ru

Задачи продолжения температурных полей по данным точечных измерений А. Н. Васильев

Вид материалаДокументы
Подобный материал:
О нейросетевом поДходЕ

к регуляризации решения

задачи продолжения

температурных полей

по данным точечных измерений


А.Н.Васильев, профессор ФМФ СПбГПУ, a.n.vasilyev@gmail.com

Д.А.Тархов, профессор ФМФ СПбГПУ, dtarkhov@gmail.com

Общая методика работы с моделями, основанными на дифференциальных уравнениях в частных производных [1-3], применяется к известной некорректной задачи, решение которой стандартными подходами затруднено. Поясним суть нейросетевого подхода авторов на примере простейшей краевой задачи

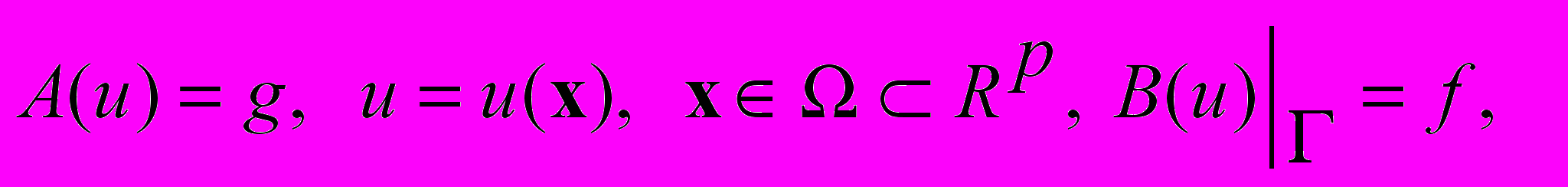(1)

здесь 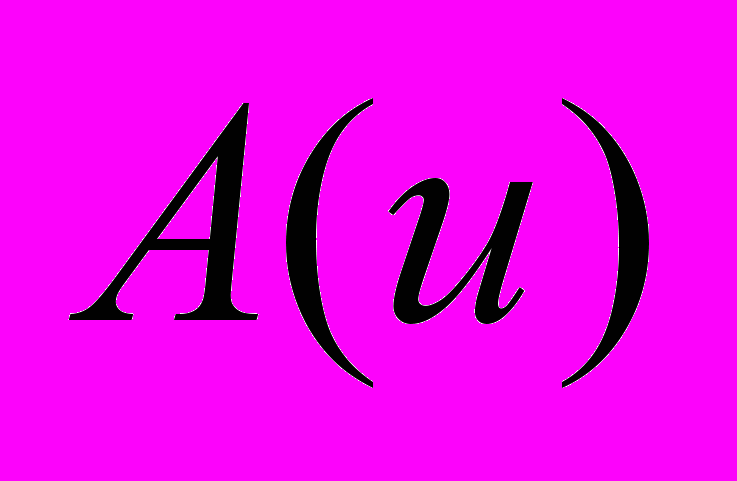– некоторый дифференциальный оператор, т.е. алгебраическое выражение, содержащее частные производные от неизвестной функции 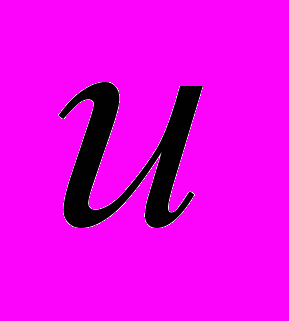, 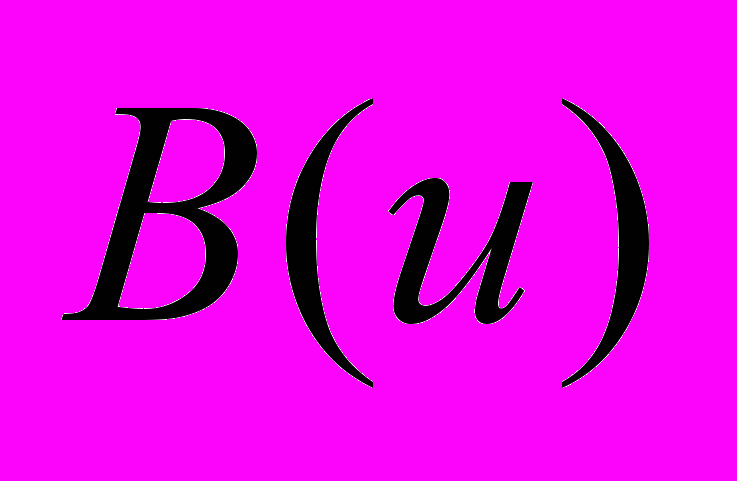– оператор, позволяющий задать граничные условия, – граница области .

Ищем приближённое решение задачи (1) в виде выхода нейронной сети некоторой заданной архитектуры

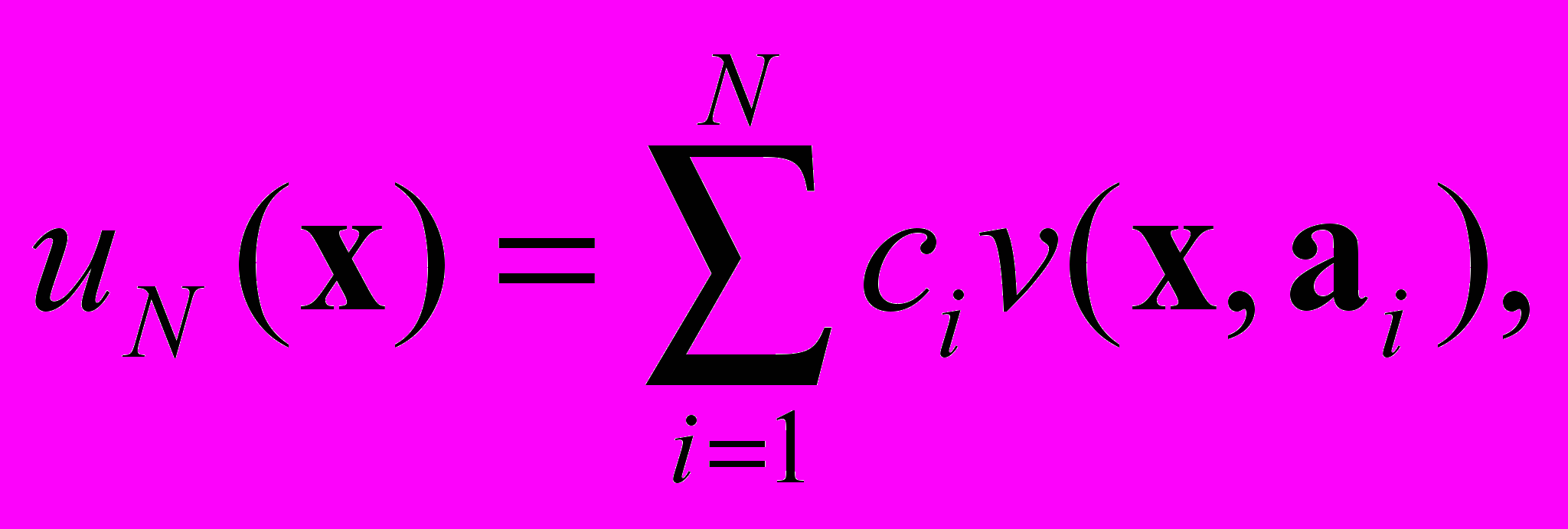(2)

веса которой – линейно входящие параметры 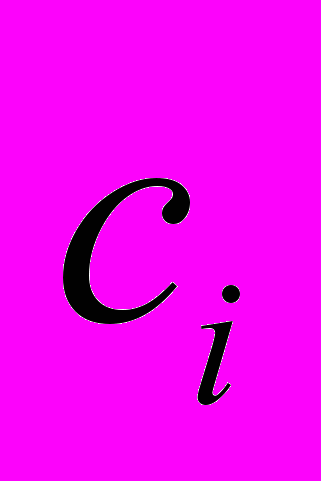и нелинейно входящие параметры – находятся в процессе поэтапного обучения сети, построенном в общем случае на минимизации некоторого функционала ошибки 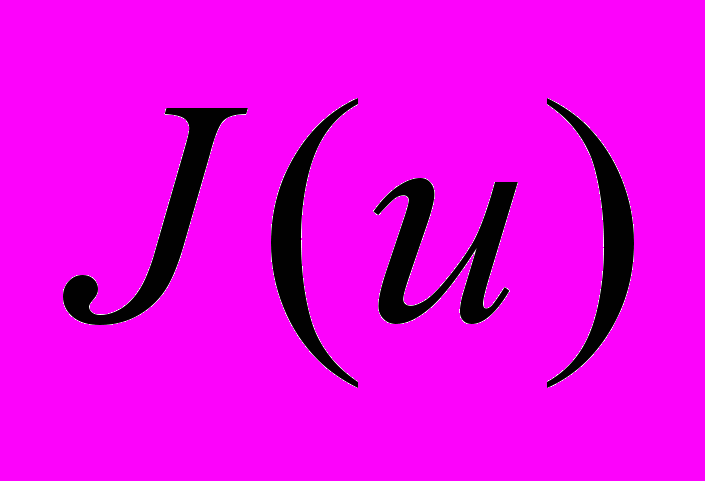вида

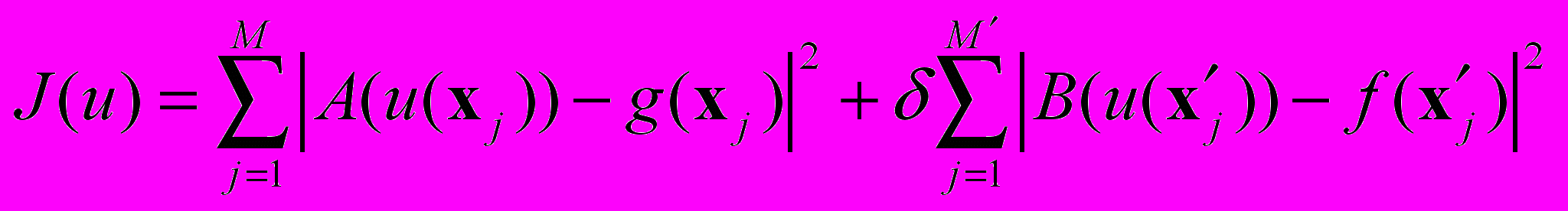. (3)

Здесь 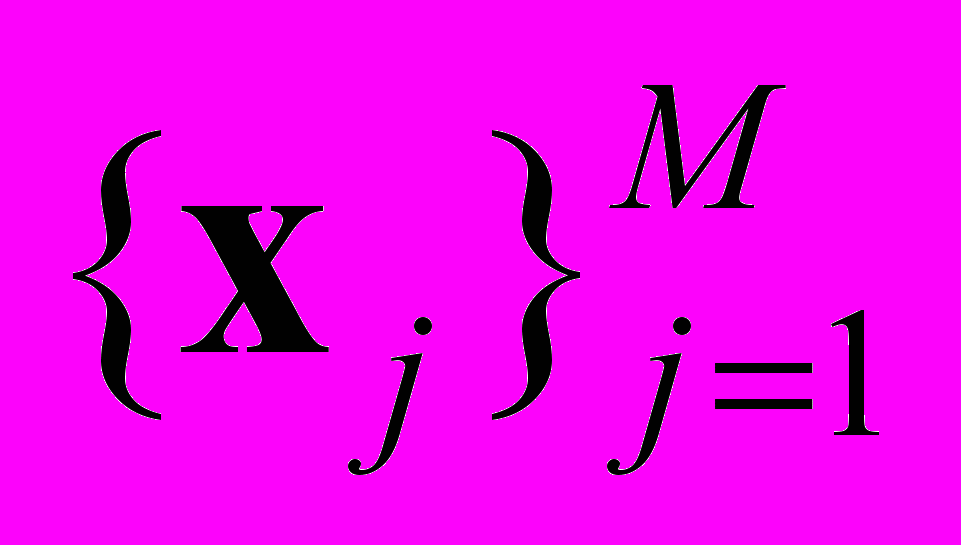– периодически перегенерируемые пробные точки в области , 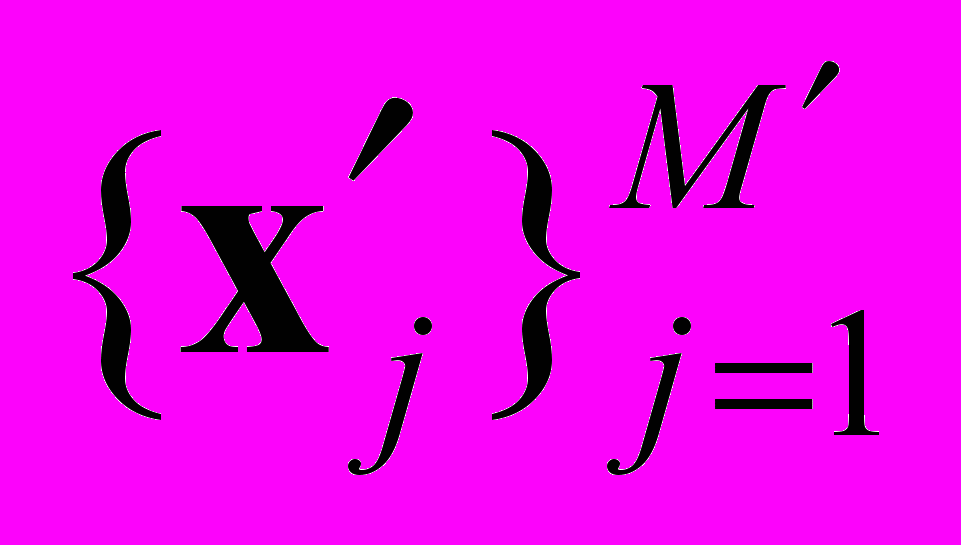– пробные точки на её границе . Возможны и другие подходы к настройке параметров нейронной сети.

Предложенная методика позволяет работать не только с простейшими краевыми задачами – ее можно модифицировать и для нестационарных задач: на примере уравнения теплопроводности для струны применим ее к эволюционным задачам и некоторым некорректным задачам.

Пусть 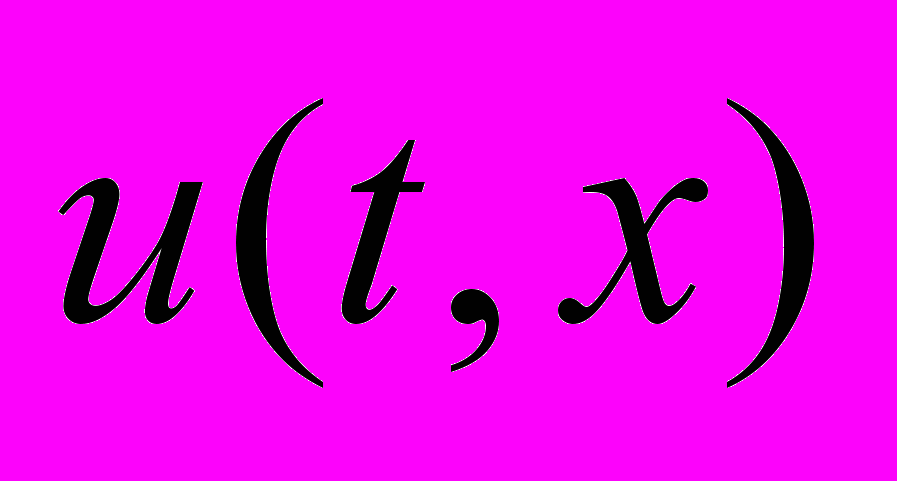, где 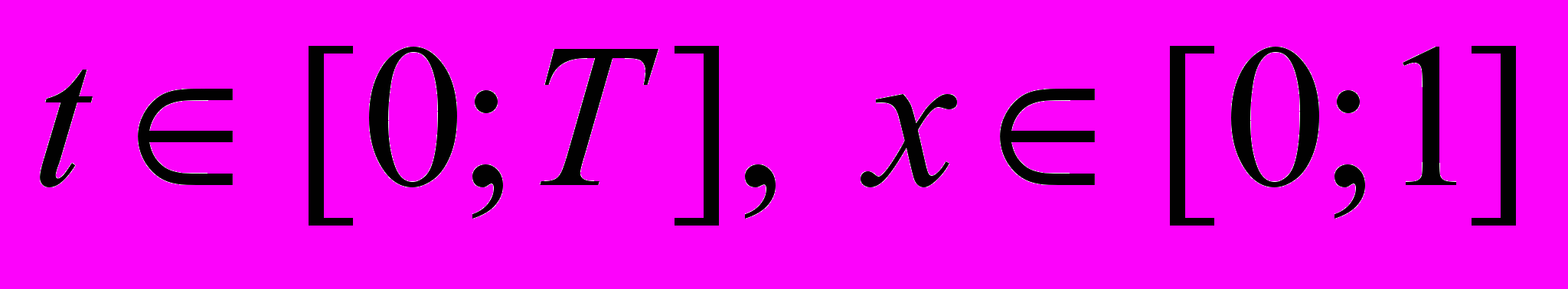, – решение неоднородного уравнения теплопроводности 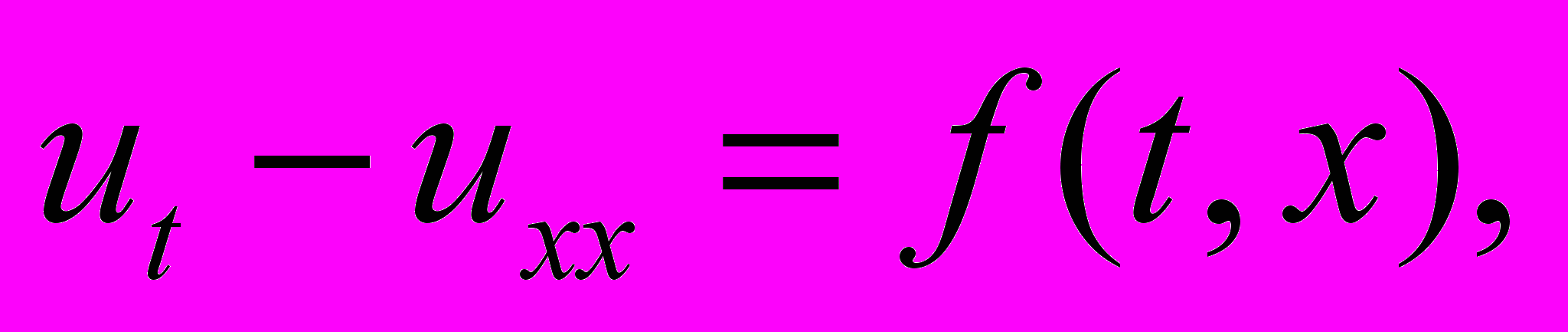удовлетворяющее краевым условиям 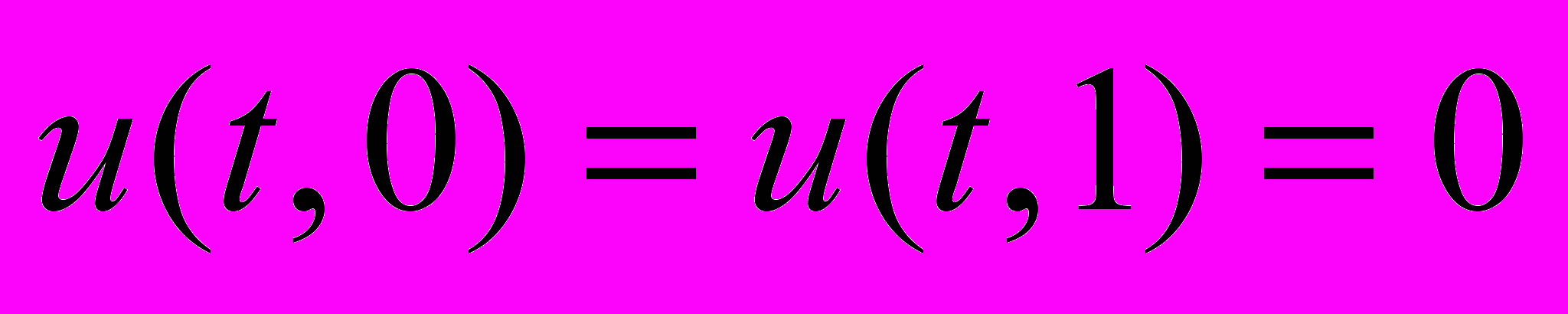и начальным условиям 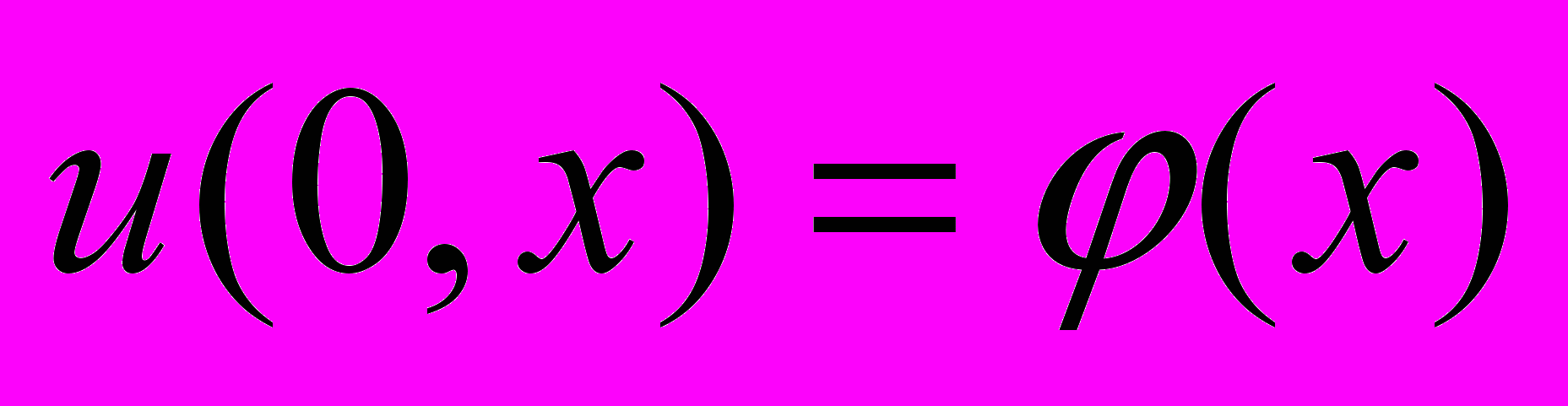. Задание этих условий позволяет решать задачу «вперёд» – и, как известно, такая задача является корректной.

Решение прямой задачи, как и других подобных задач, можно искать в виде нейросетевого разложения

,

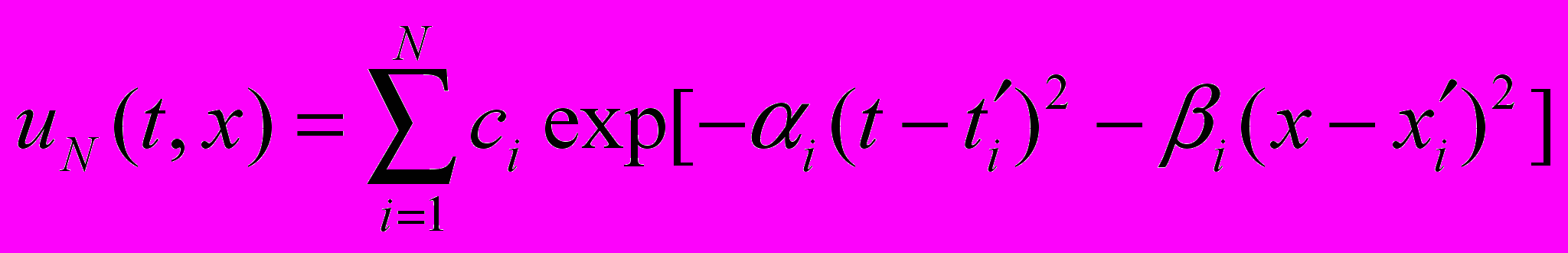параметры которого настраиваются на основе минимизации функционала ошибки, взятого в форме




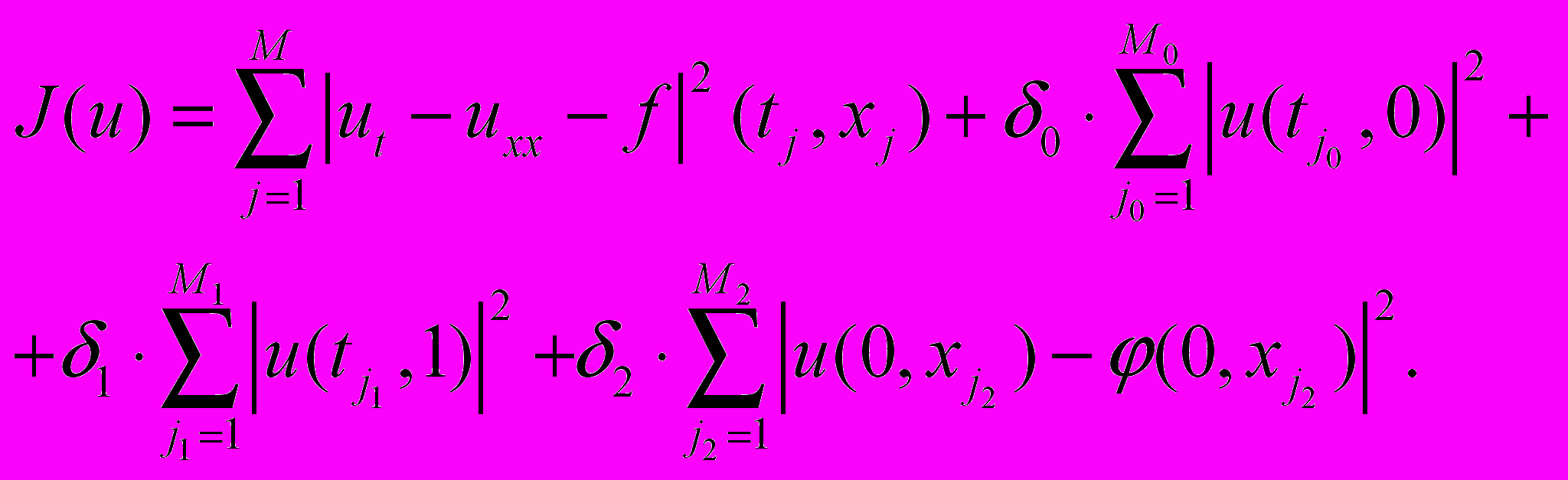
Формально начально-краевые условия позволяют искать решение задачи «назад»: определить 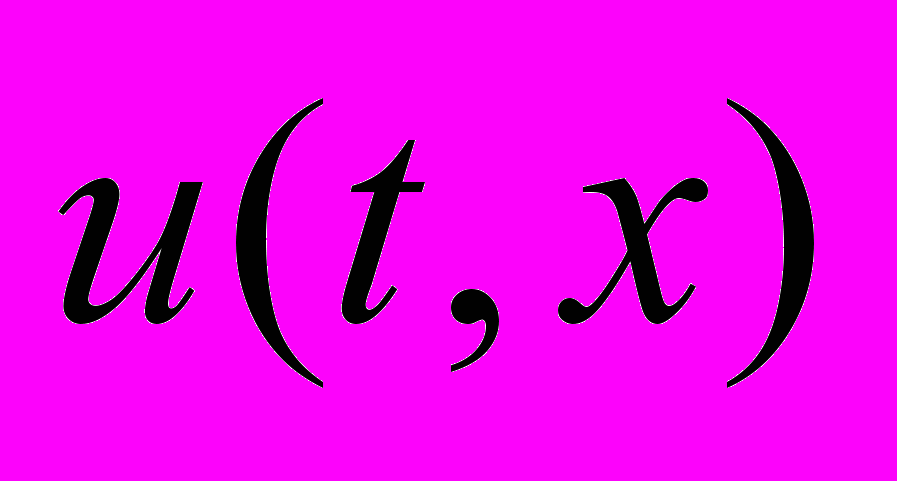, , 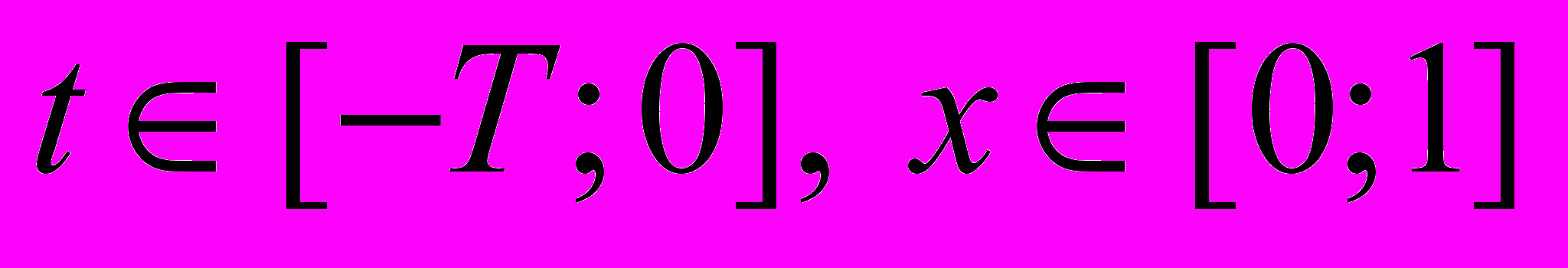однако такая постановка делает задачу некорректной. Наш подход позволяет получить устойчивое решение этой задачи.

В качестве другого примера некорректной задачи приведем задачу продолжения нестационарных полей по приближенно известным данным точечных измерений. А.А. Самарский и П.Н. Вабищевич [4] строили регуляризацию решения такой задачи посредством восстановления начальных условий (при заданных краевых условиях) по набору точечных данных (задача управления). При предлагаемом нейросетевом подходе решение как прямой, так и обратной задачи строится единообразно.

Перейдем к решению обратной задачи. Заменим начальное условие соотношениями 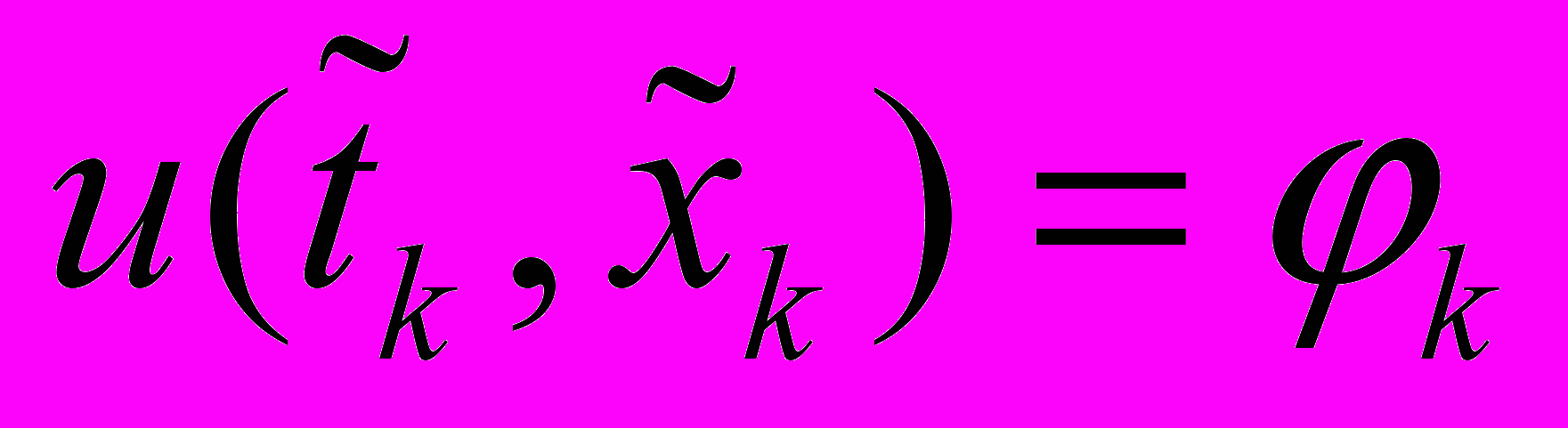, 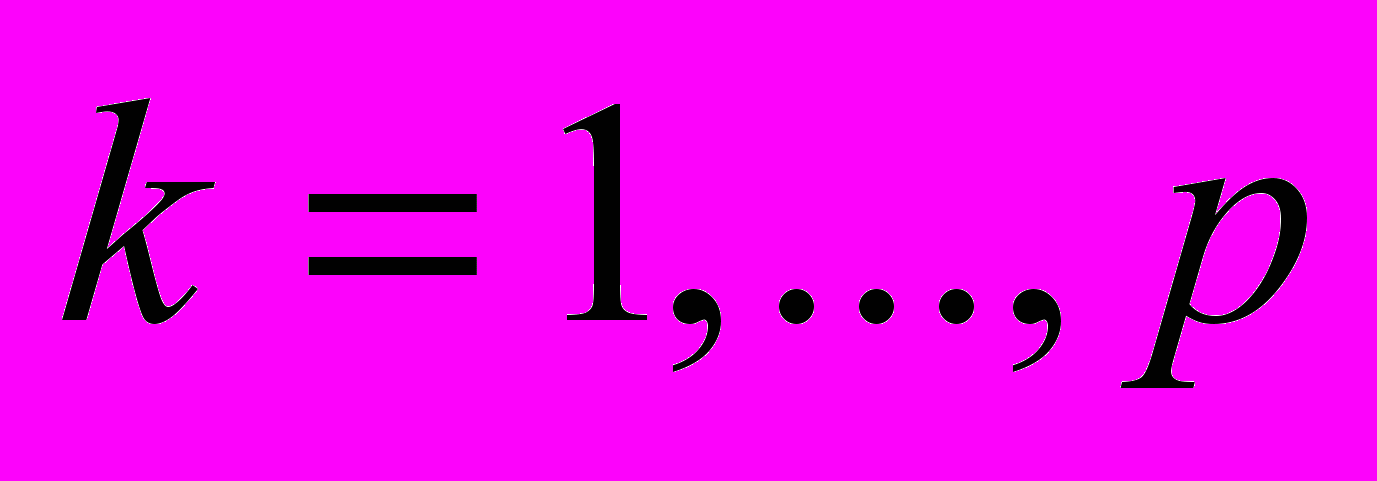в точках некоторого множества 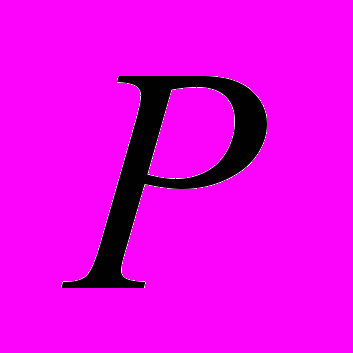. Здесь 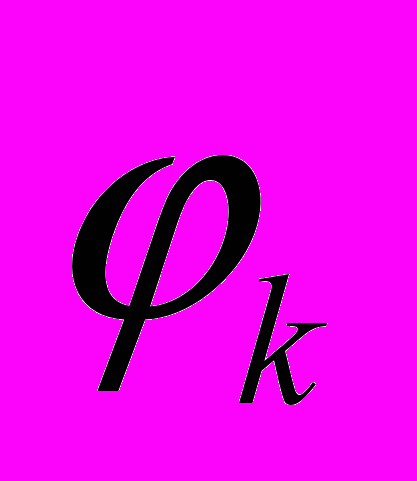– заданные с некоторой ошибкой 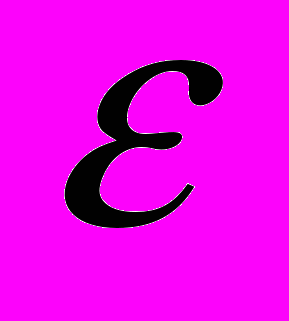опытные данные.

Приближённое решение этой задачи ищем, как и ранее, в виде нейросетевой функции, имеющей, к примеру, тот же (или аналогичный приведенному) вид 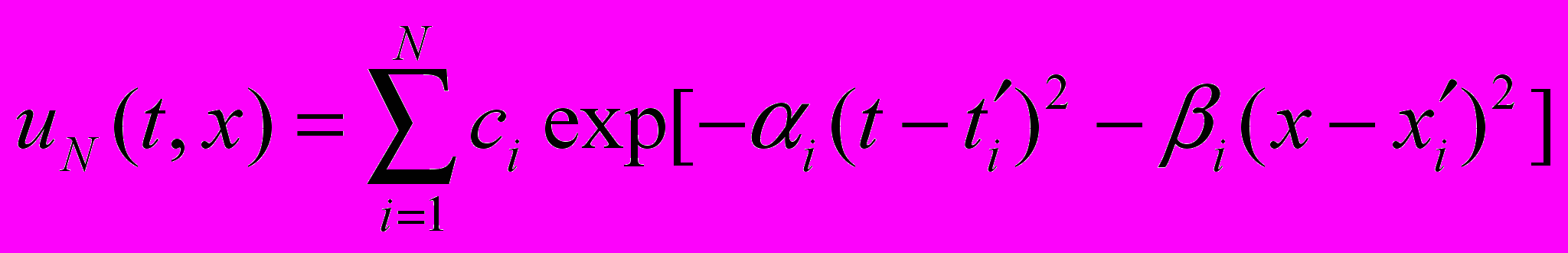. В качестве нейросетевых базисных функций могут использоваться и другие, например, мультиквадрики .

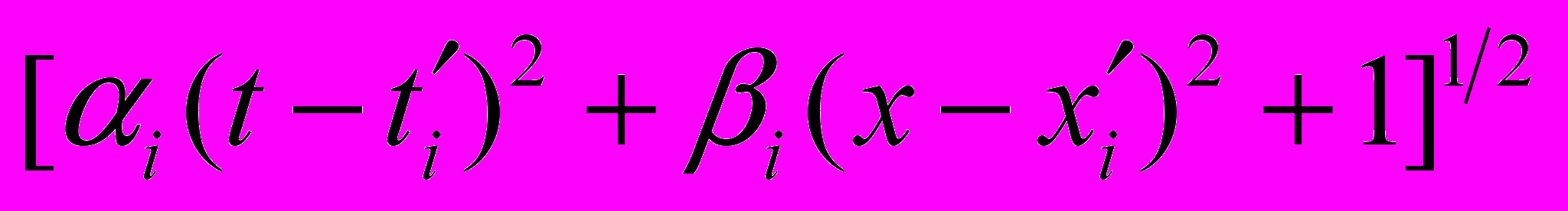Процесс обучения нейронной сети основан, как и ранее, на минимизации функционала ошибки, взятого, например, в виде



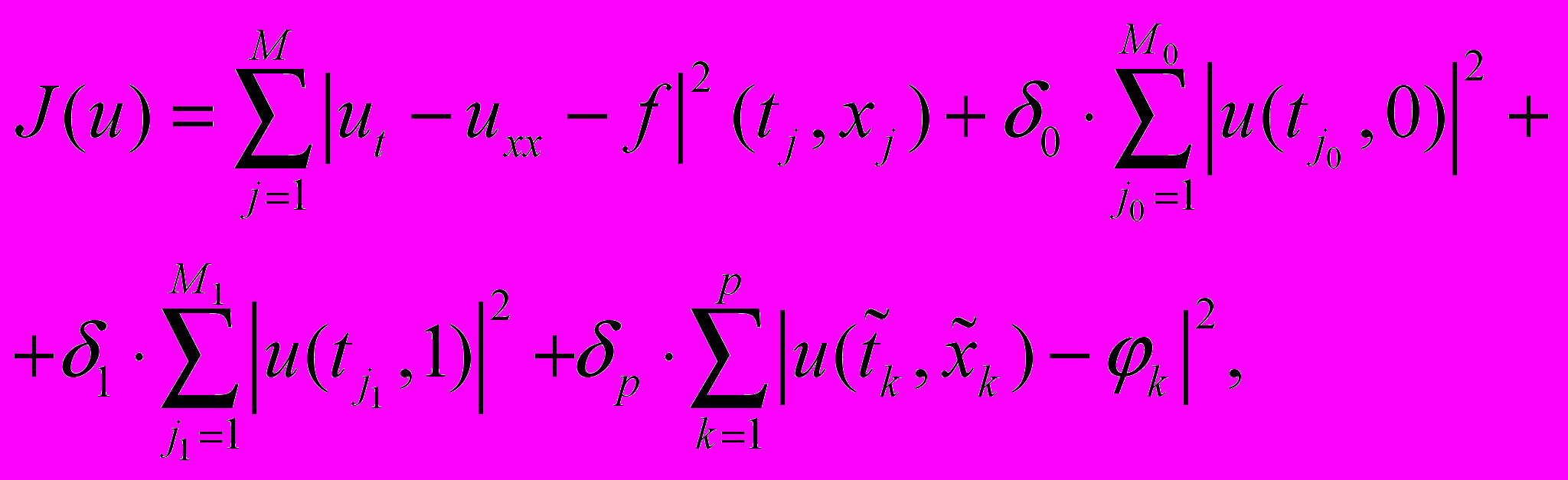
где 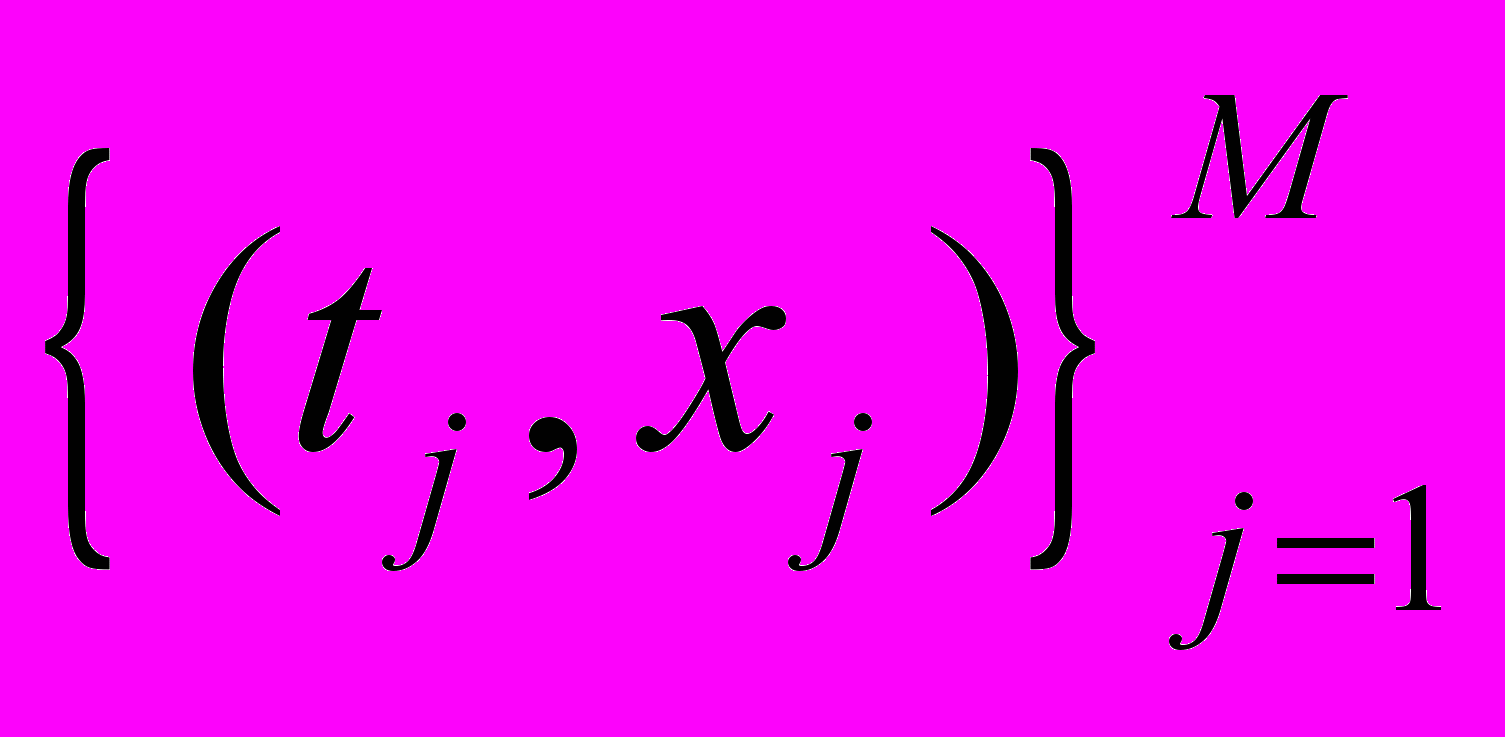, , 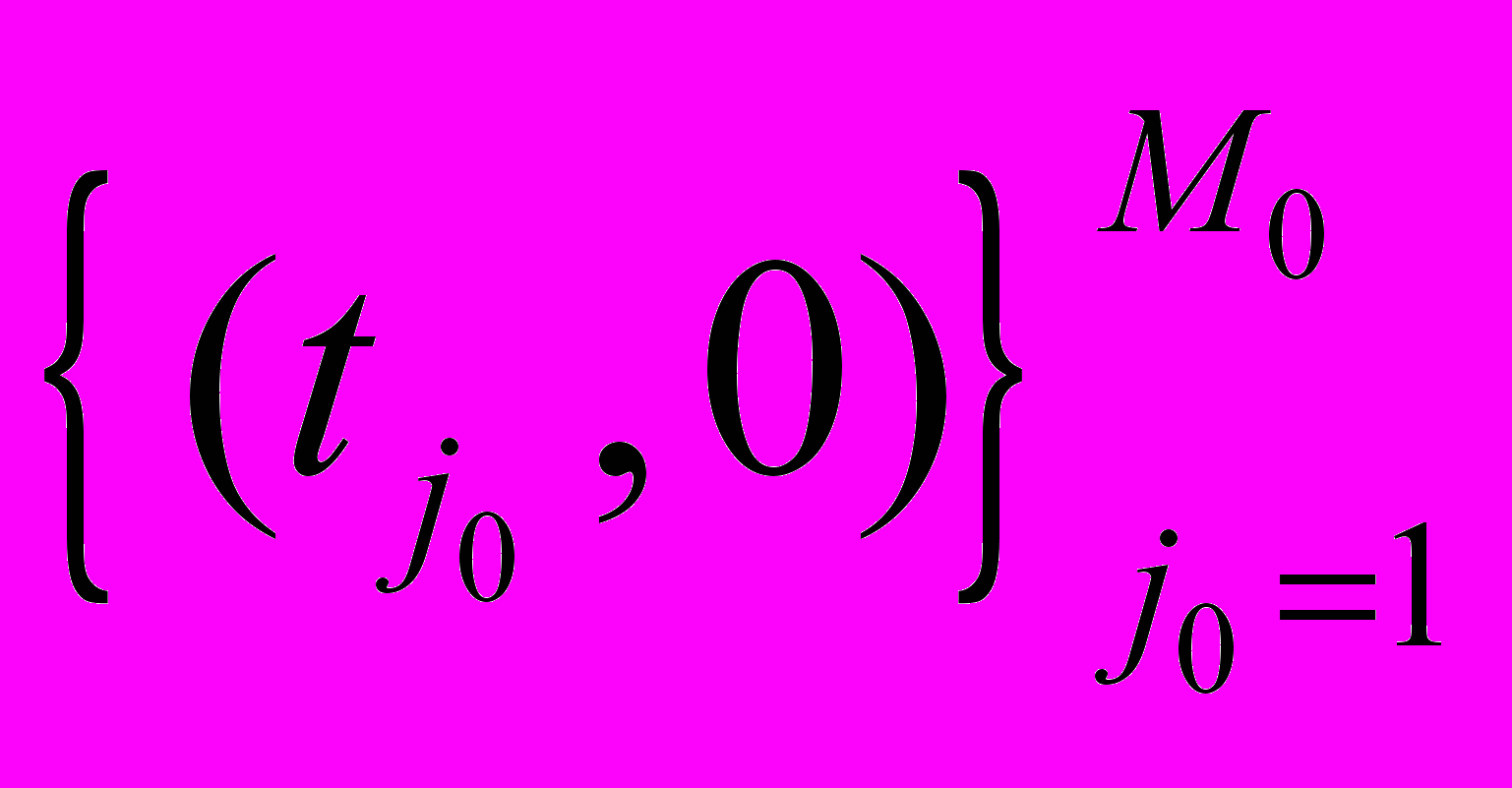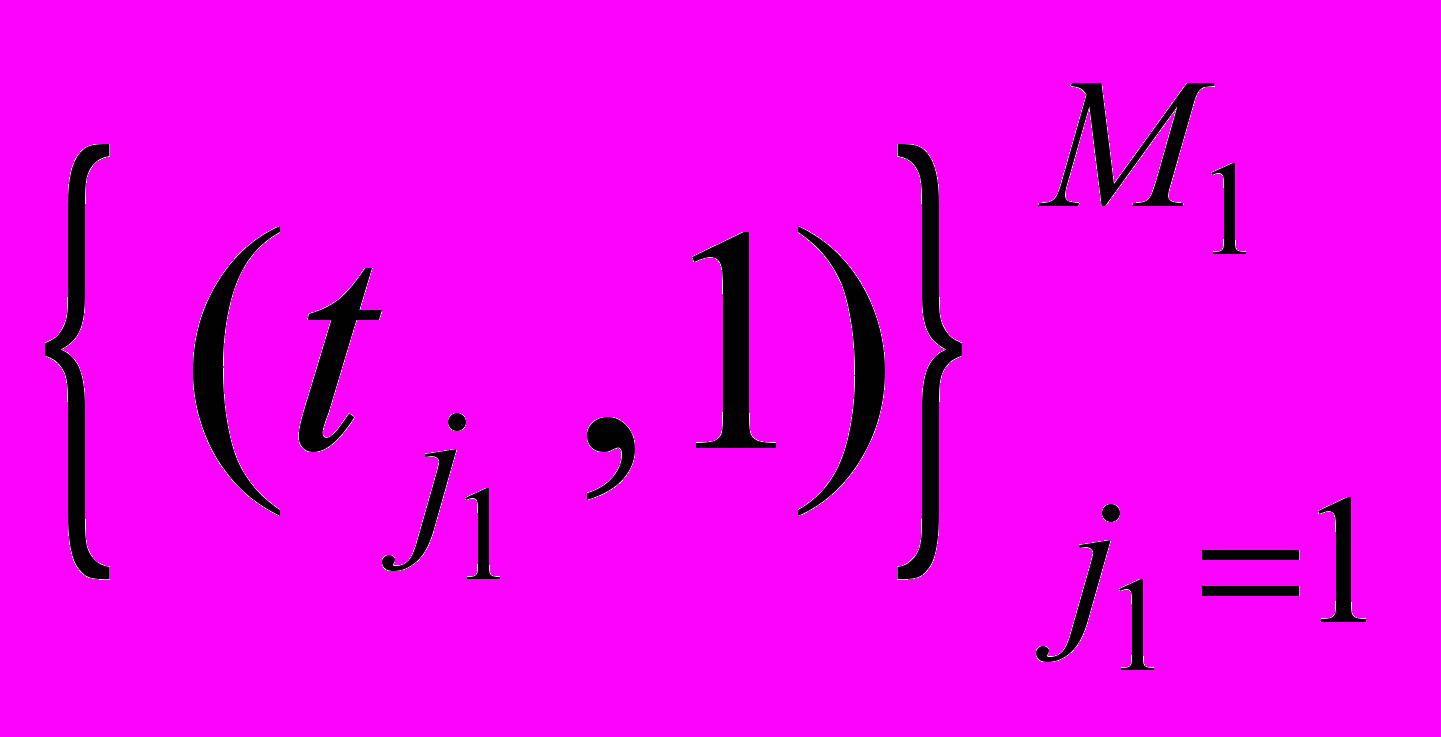– наборы тестовых точек внутри области, на левой и правой границах. Эти наборы тестовых точек перегенерируются после определенного числа шагов процесса обучения.

Отметим, что в этой простой задаче при определенном выборе типа нейроэлементов (например, гауссианов) было получено и явное относительно настраиваемых параметров, хотя и очень громоздкое выражение для функционала ошибки. Использование подобных явных формул для функционала, несомненно, ускоряет процесс обучения сети. Но в данном случае при проведении вычислений при оптимизации применялся общий подход.

В качестве модельного (определяемого в подобной постановке) решения использовалась функция 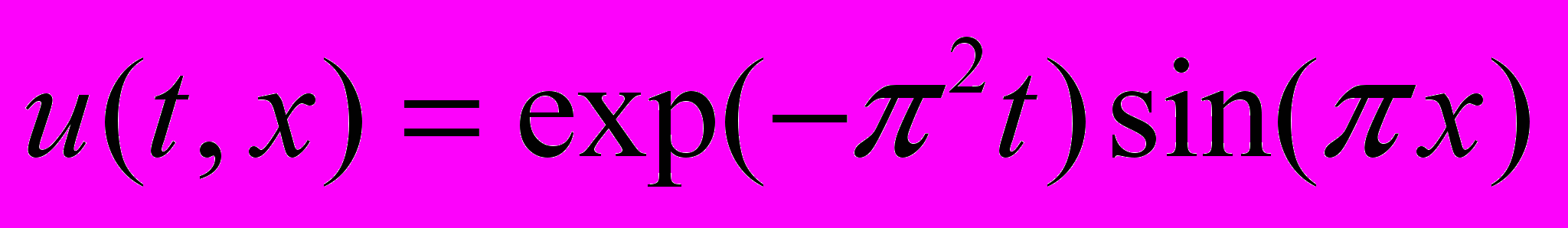, значения которой задавались с ошибкой 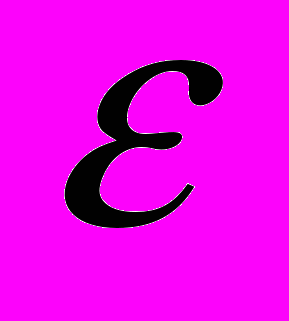в наборе точек 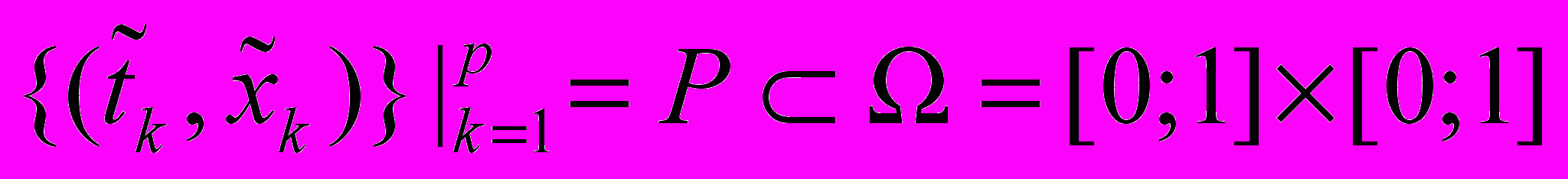. Рассматривались случаи разного числа точек 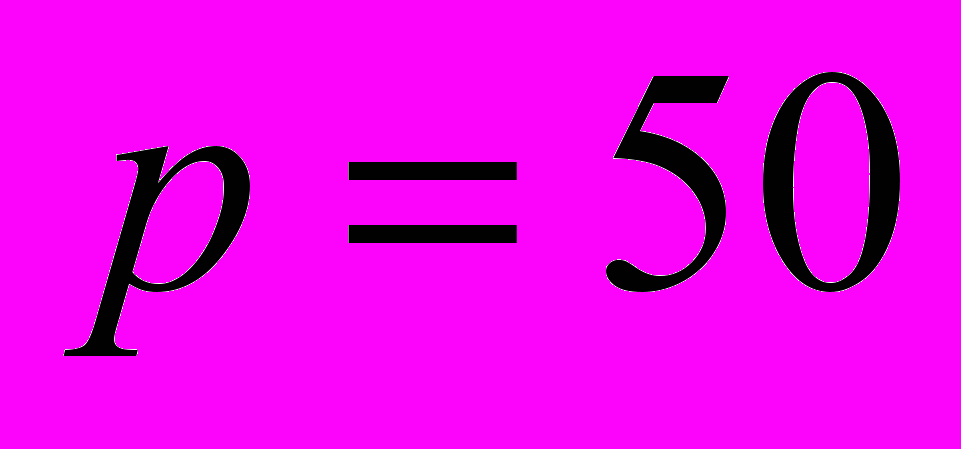и 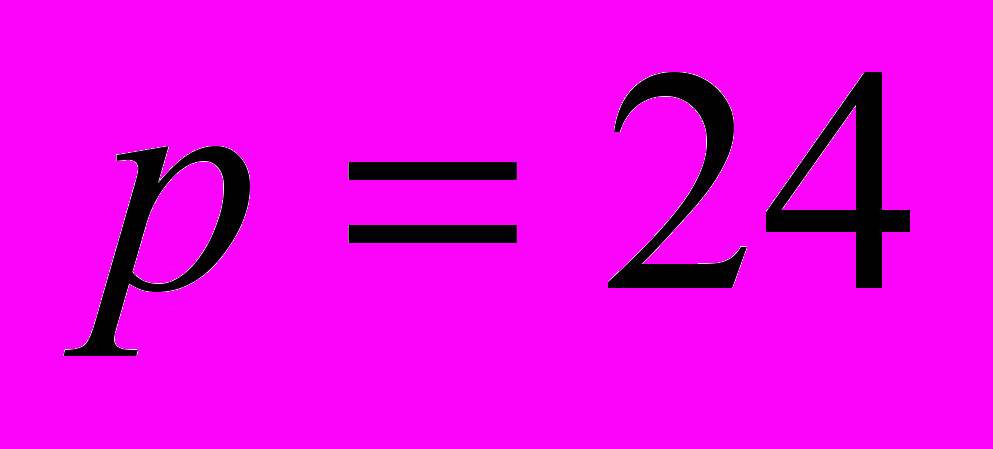, а также варианты задания «опытных данных» с разной точностью: 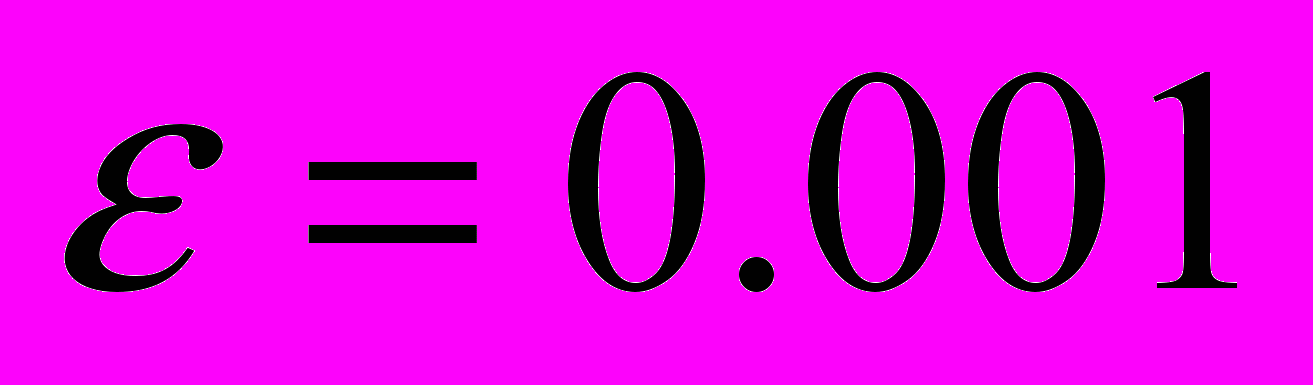, 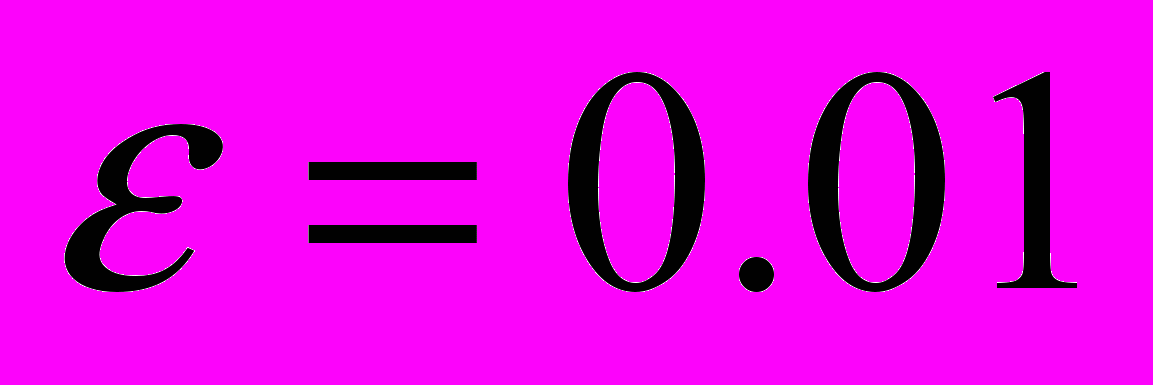и .

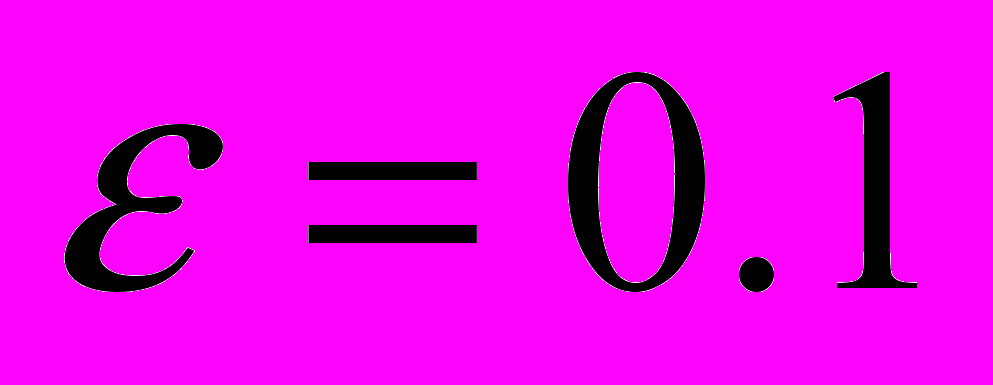В качестве приближенного решения рассматривалась нейросеть из 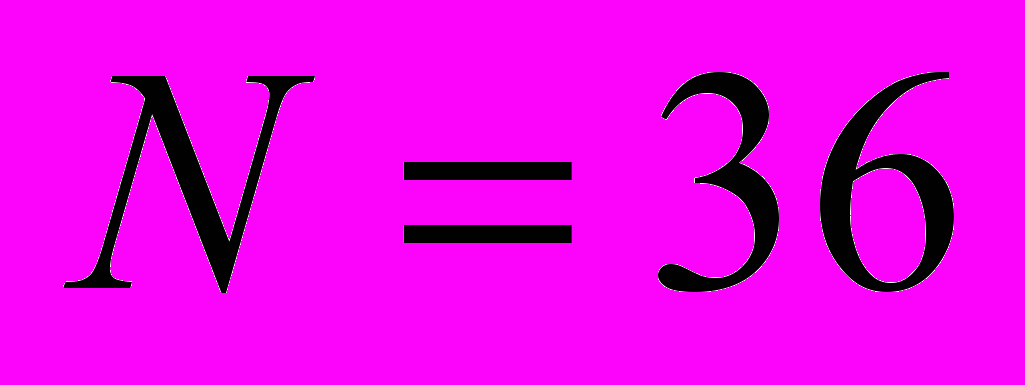«круговых» гауссовых экспонент («эллипсоидальные» гауссианы также применялись, но никакого выигрыша не дали). Для обучения сети использовался метод плотного облака, проявивший себя в этой задаче лучше модифицированного метода многогранника [5], радиус облака – 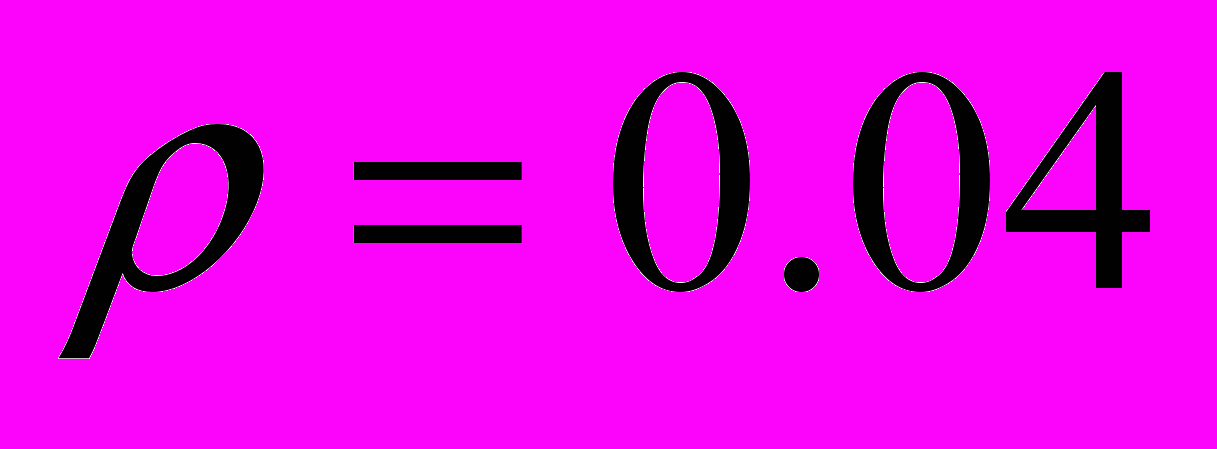. Изменение в точности задания «экспериментальных данных» с 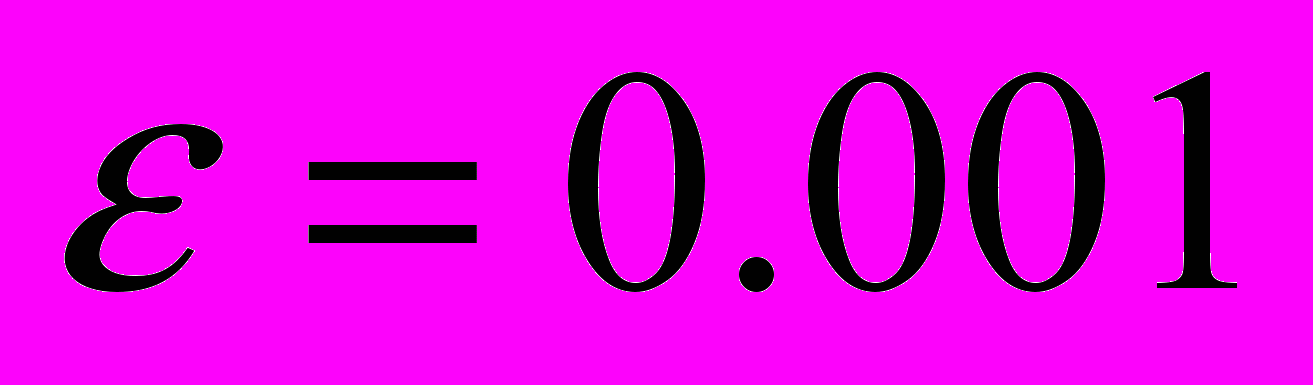на 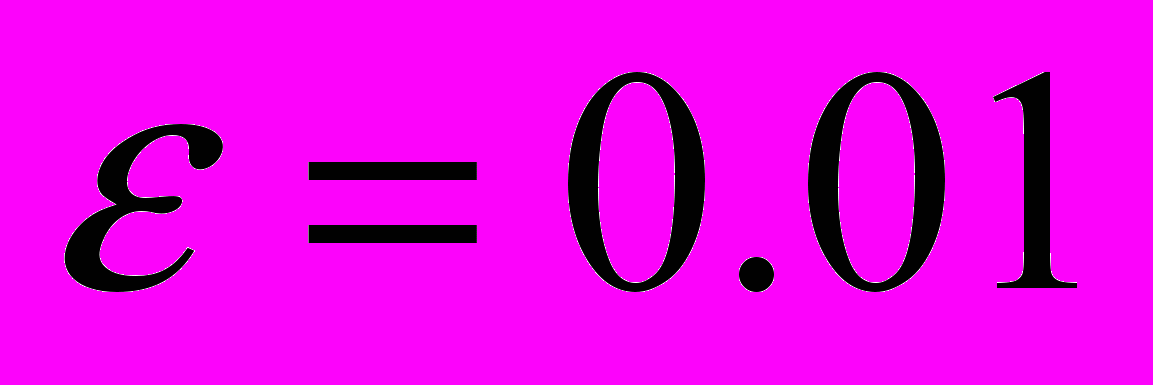(и даже на 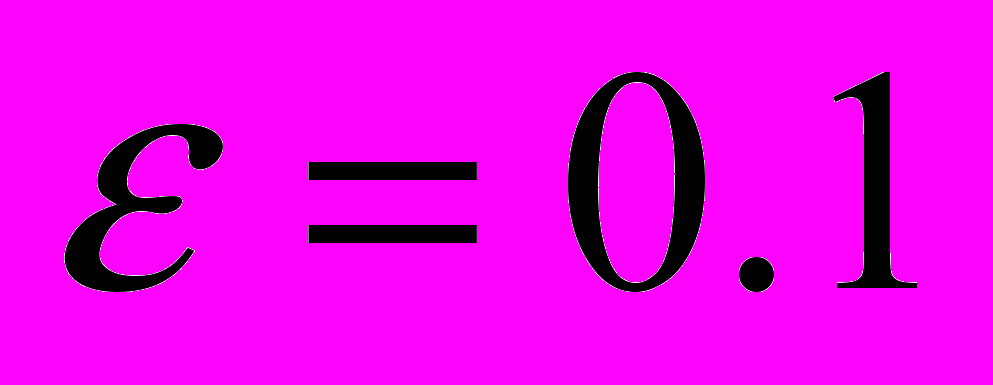) не привело к существенному изменению качества построенного нейросетевого решения. Вычисления проводились в среде Mathematica 6.


Результаты вычислений для значений 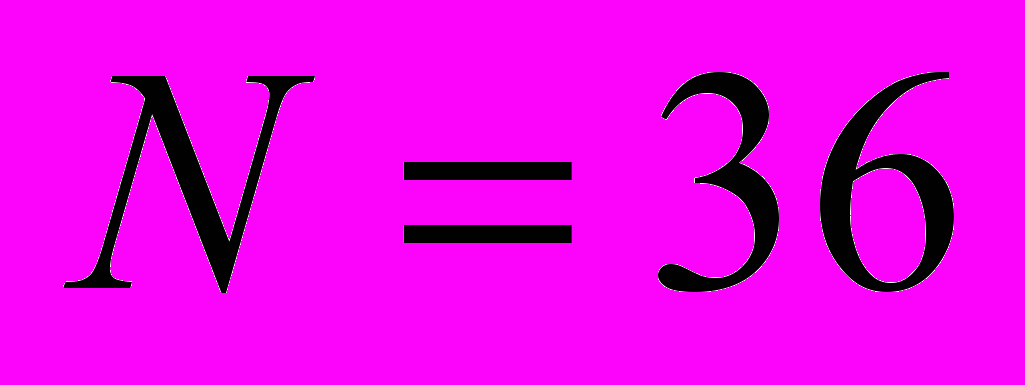, , 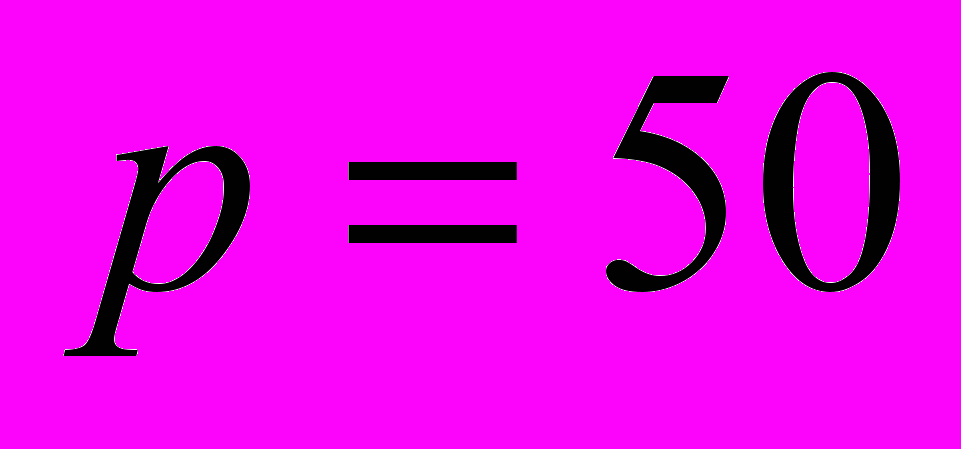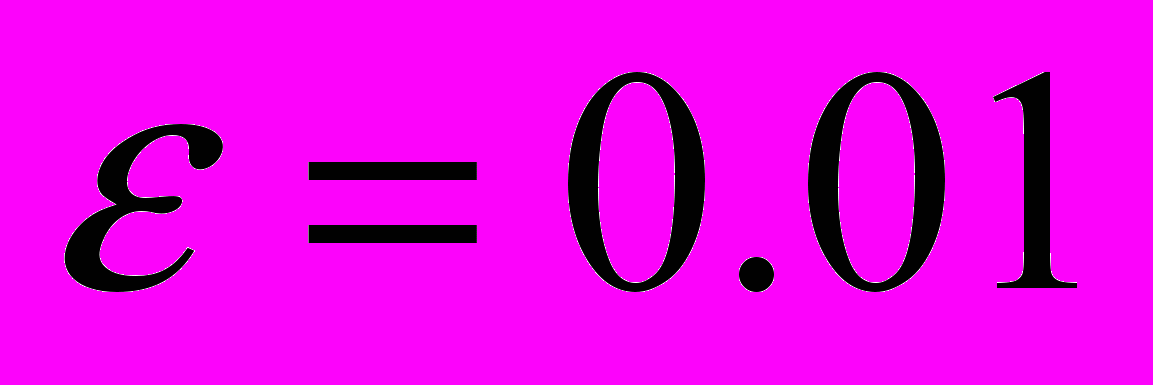приведены ниже.




Рис.1. График решения 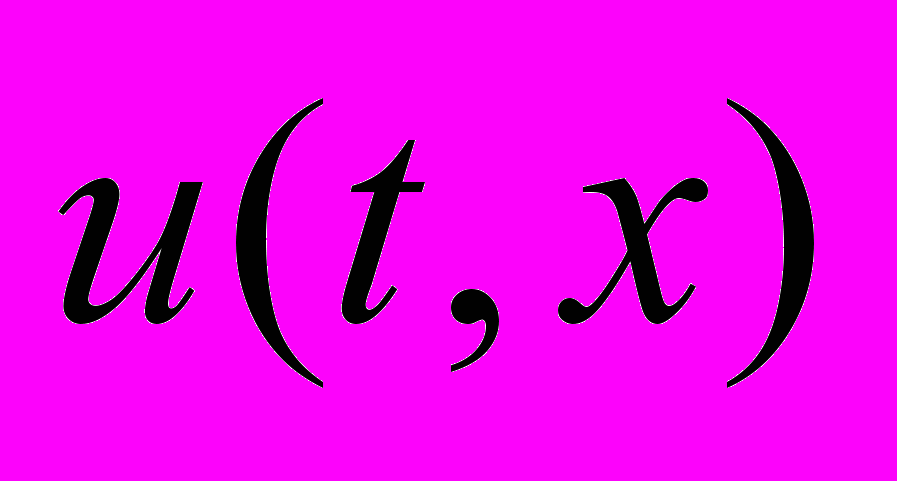Рис.2. Начальные условия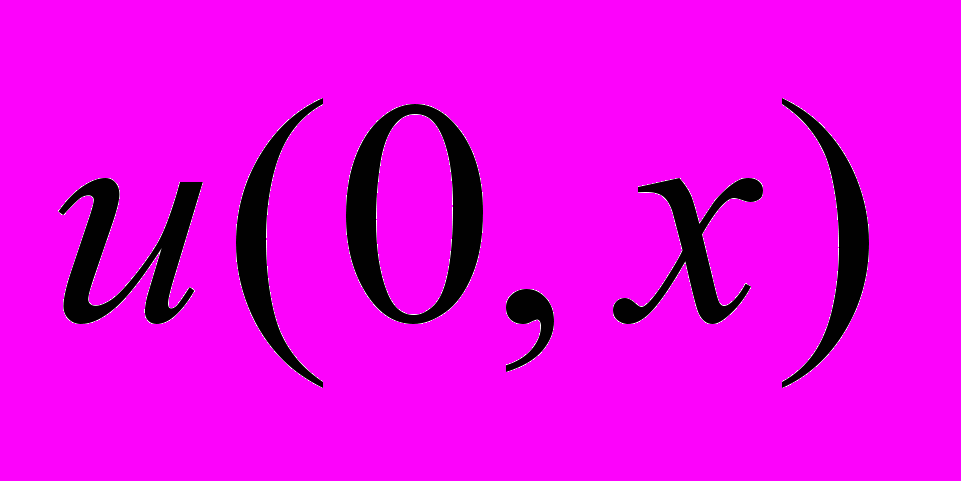


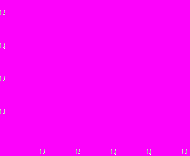
Рис.3. График решения 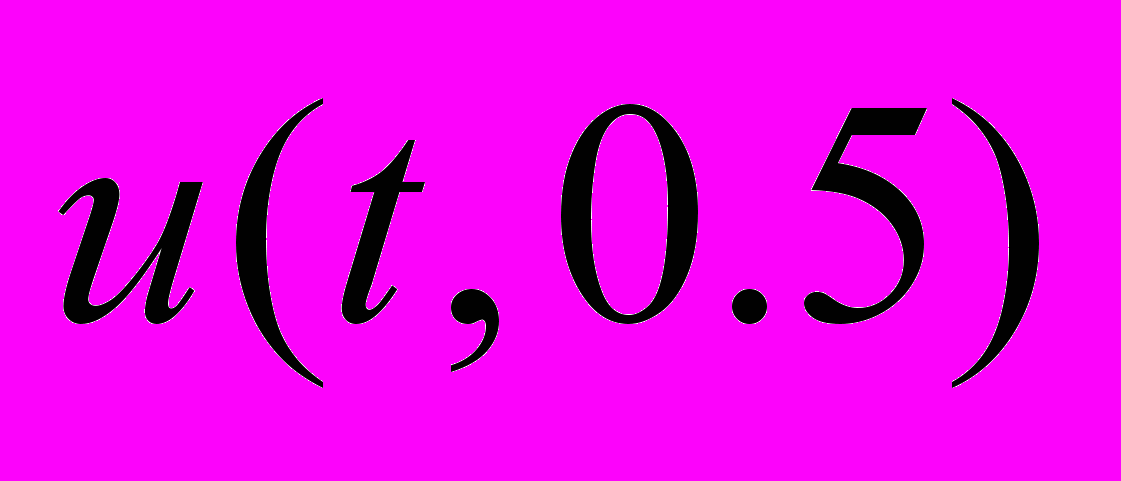, Рис.4. График решения ,




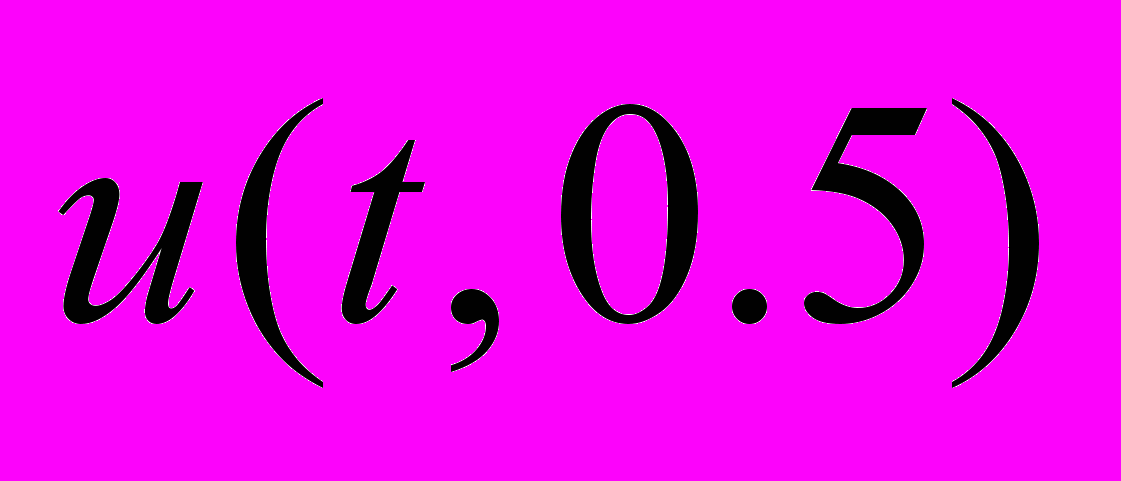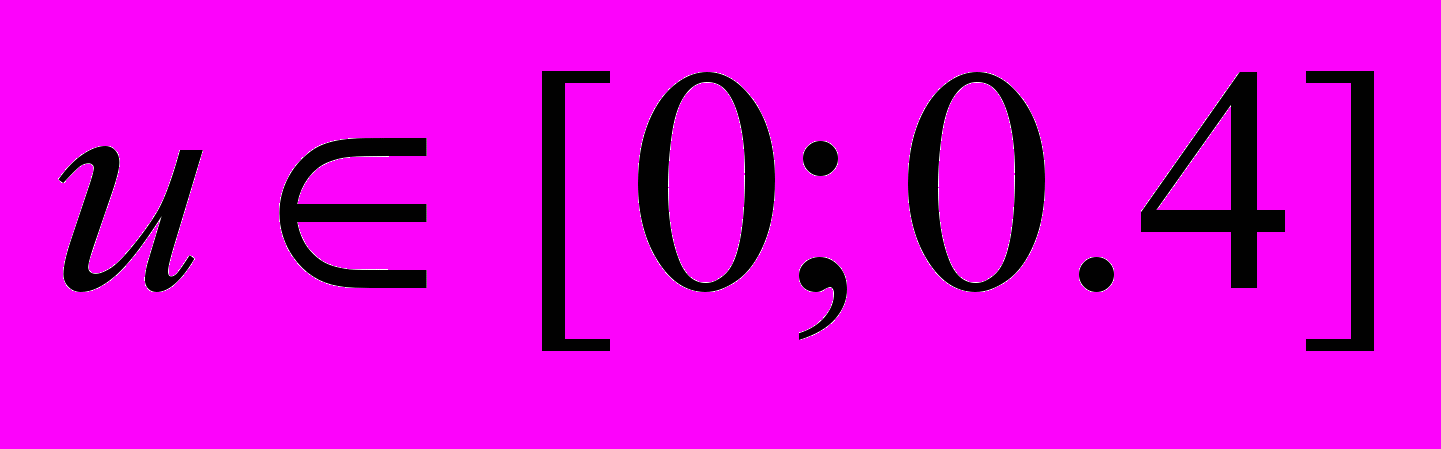
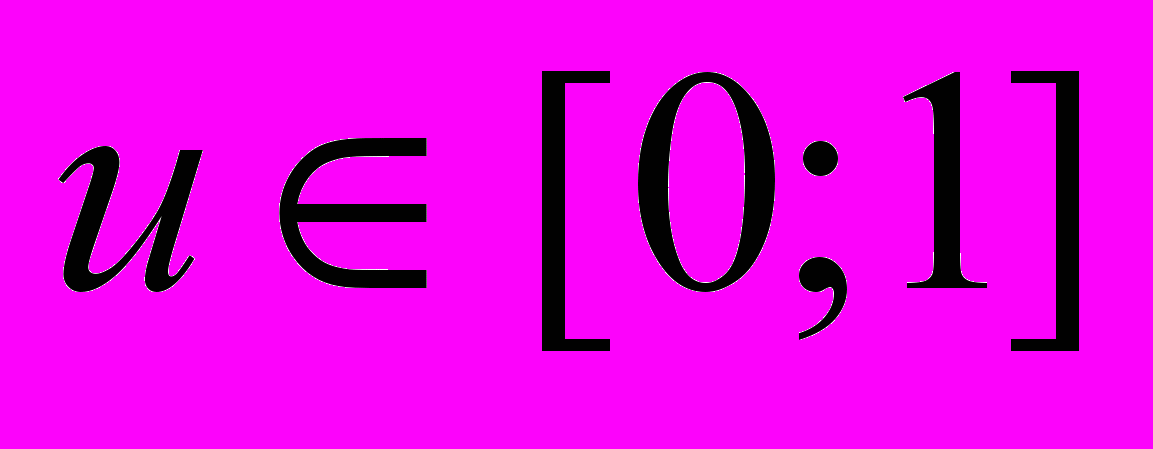
Приведем также результаты вычислений для , , .



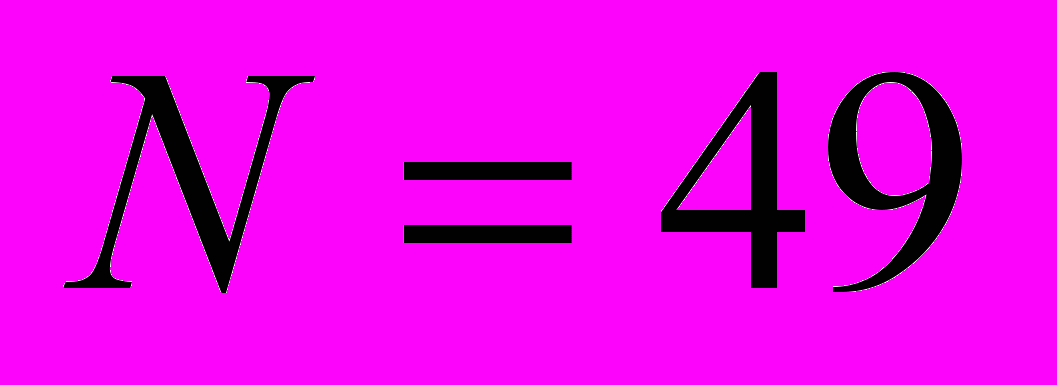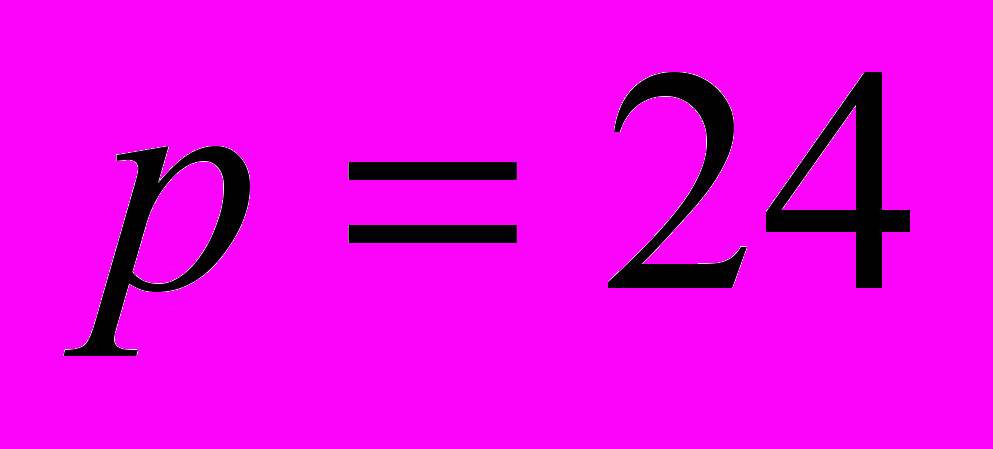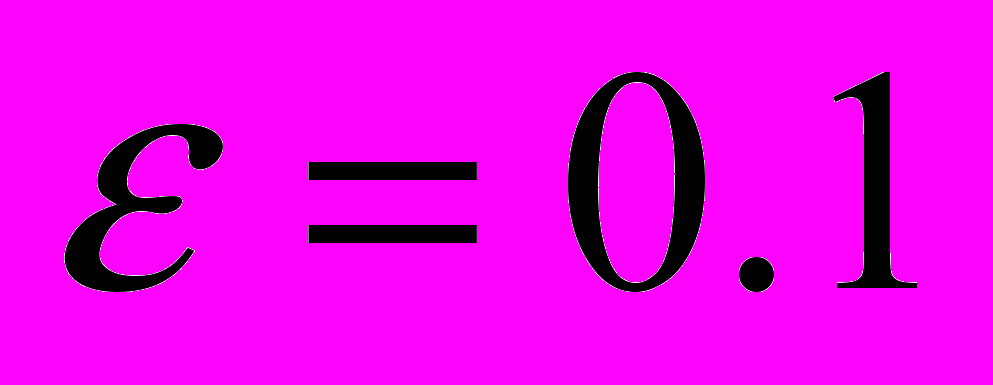Рис.5. График решения 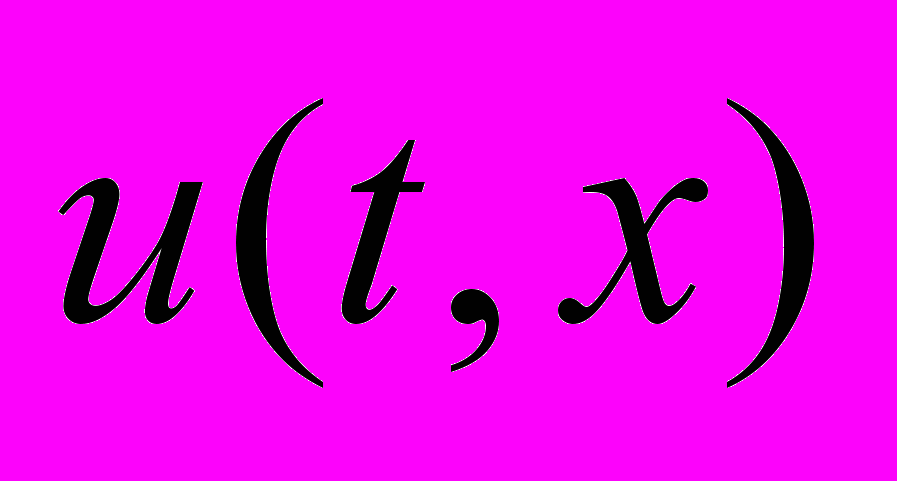Рис.6. Начальные условия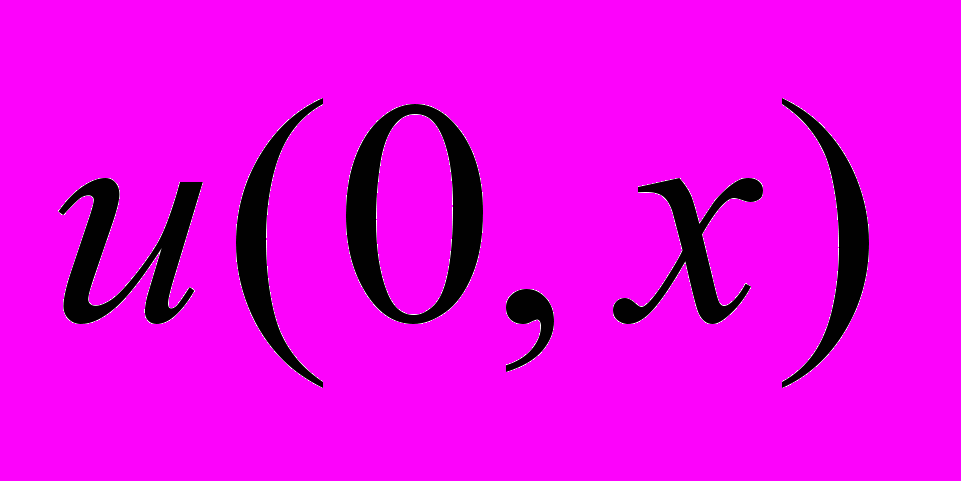




Рис.7. График решения 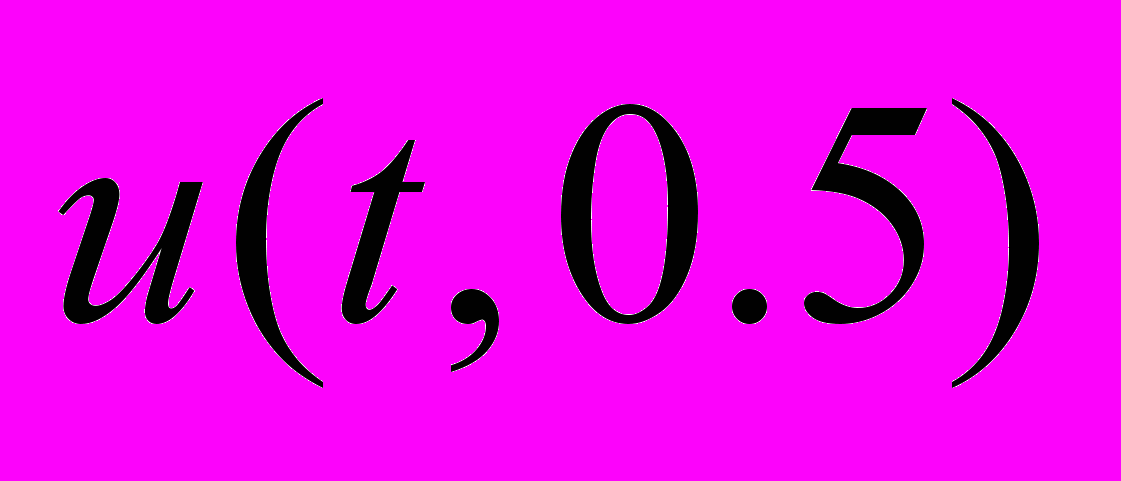, Рис.8. График решения ,


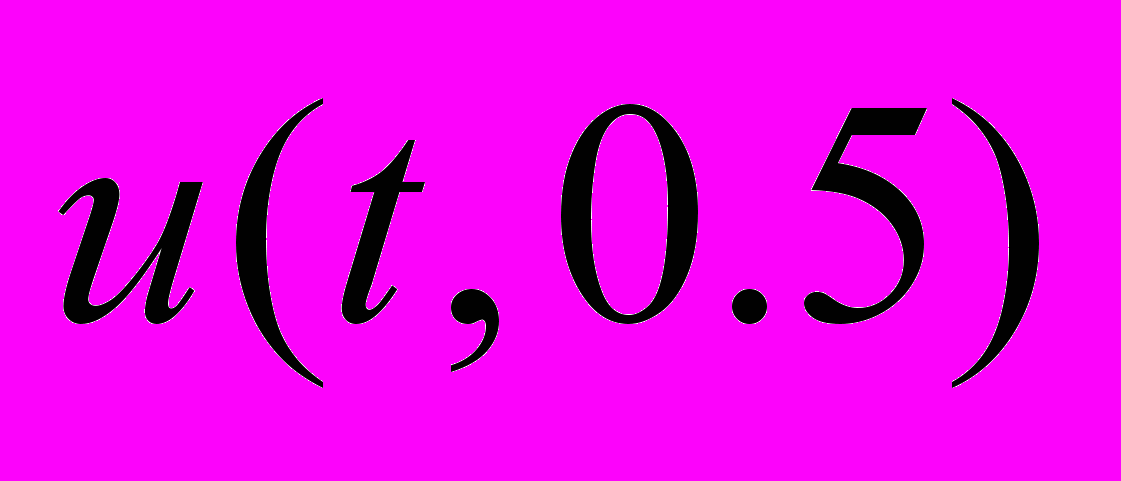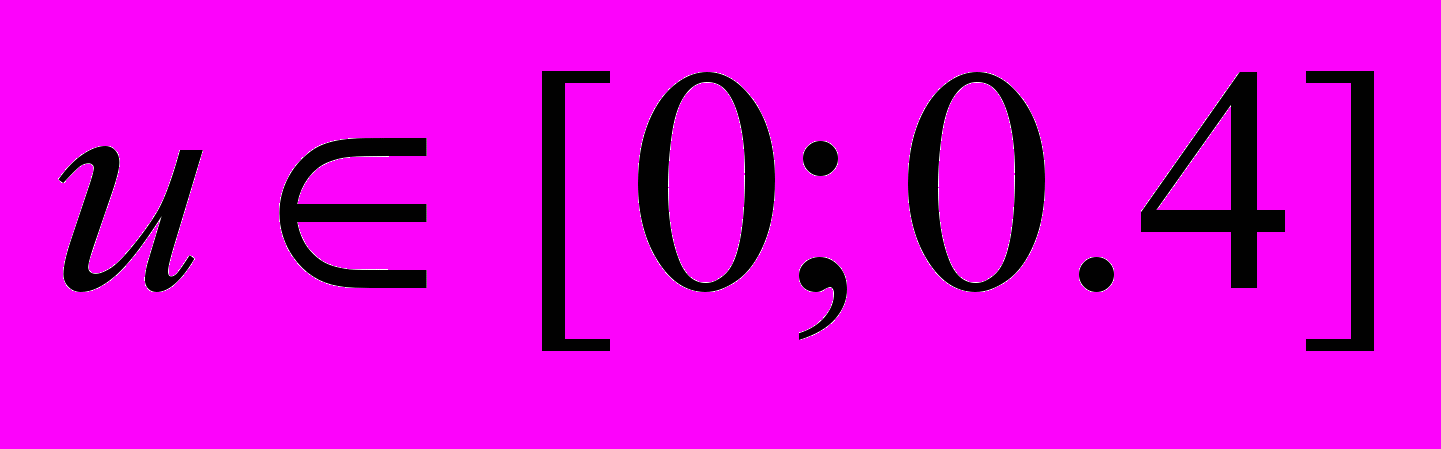
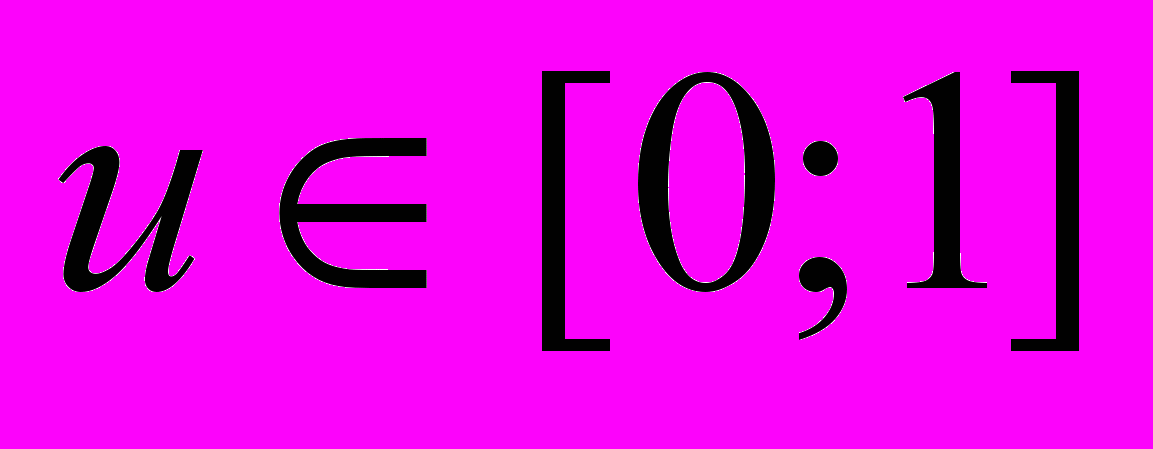
Вид исходного решения отслежен, оно восстанавливается с ошибкой .

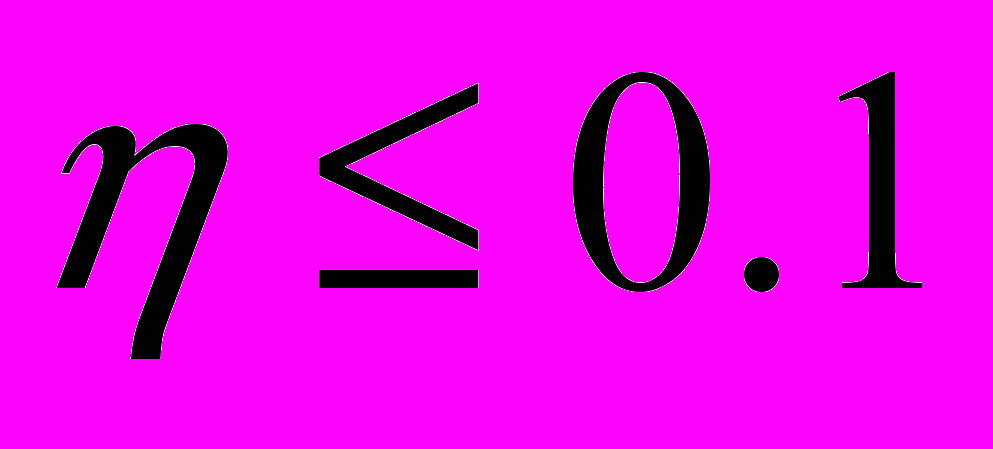Исследовались разные варианты инициирования начальных значений параметров обучаемой нейросети – результат оказался ожидаемым: чем ближе исходная ненастроенная сеть к искомому решению, тем быстрее (за меньшее число эпох обучения) выстраивается приближенное нейросетевое решение задачи данной точности, но неудача в выборе начального приближения может быть скомпенсирована достаточно большим количеством итераций; увеличение – числа используемых функций – увеличивает число итераций для достижения предписанной точности и время каждой операции (рассматривались сети из , 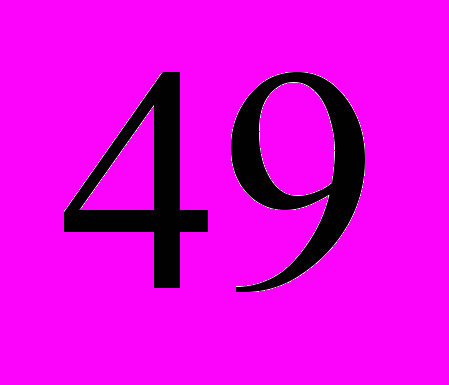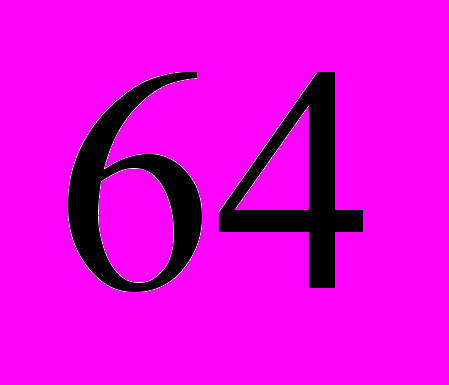и 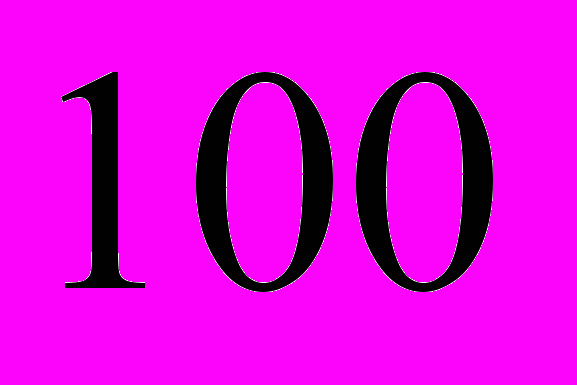гауссианов).

В случае линейных задач возможны и другие подходы к обучению нейросетей: например, метод интегральных представлений [1]. При таком подходе используются нестандартные нейросетевые базисные элементы – решения, которые порождены нейросетевыми разложениями данных Коши при 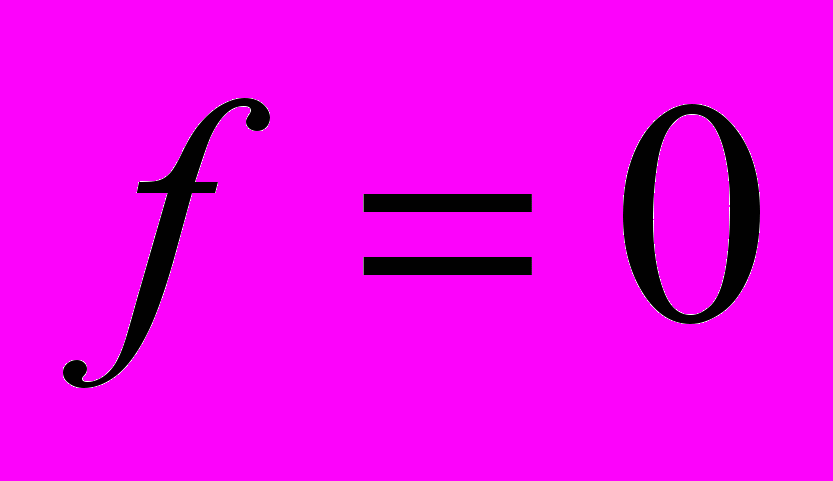: к примеру, для гауссовых пакетов – это нейросетевые функции вида

, .



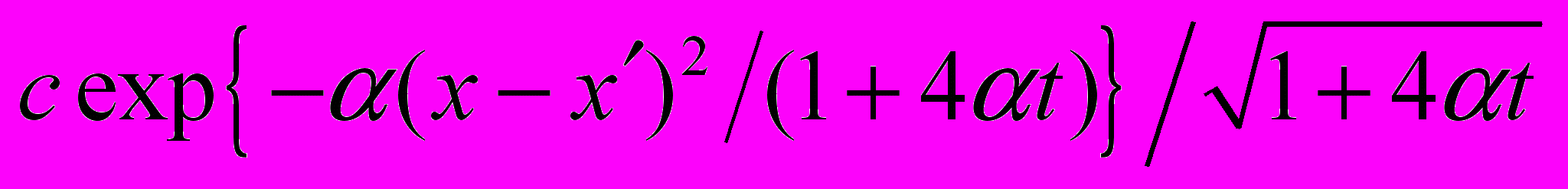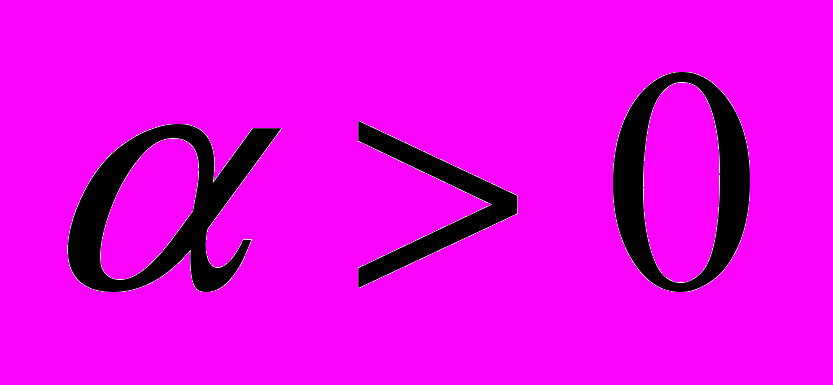Рис. 9. Аппроксимация данных Коши при втором подходе ()


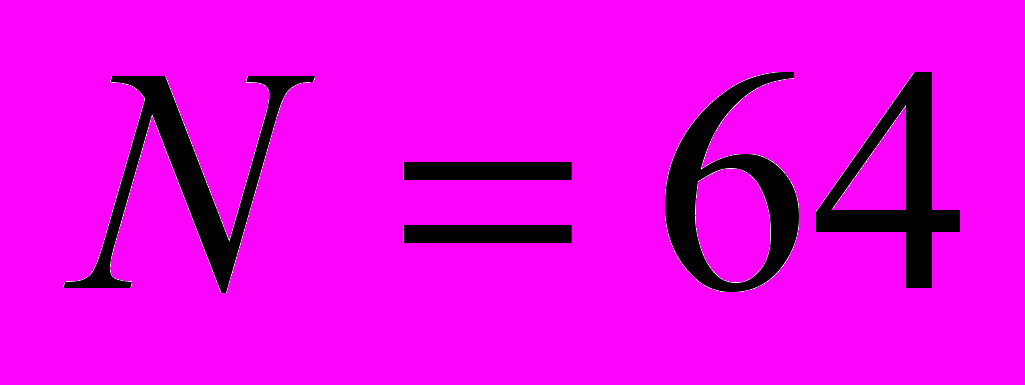При этом подходе в функционале ошибки имеются лишь слагаемые для данных Коши и краевых условий. Качество приближения при этом частном подходе весьма хорошее.


Построенное таким образом нейросетевое приближение для решения задачи можно рассматривать как его регуляризацию. Аналогичный подход можно применить и к другим некорректным задачам такого рода. Подобные построения могут быть сделаны для выделения множеств решений интегральных уравнений, интегро-дифференциальных и иных уравнений, при этом в полной мере могут быть использованы преимущества нейросетевого подхода в случае задач со сложной геометрией, с нелинейностями, с кусочными данными, при решении серии задач с уточняемой постановкой и др. Рассмотрение указанного примера лишь несколько упрощает проведение численного эксперимента, но нисколько не умаляет общность предлагаемого метода.


Несомненный интерес может представлять
  • сравнительный анализ использования различных нейросетевых функциональных базисов (в частности, разнородных),
  • использование нестандартных нейросетевых базисных элементов (например, решений, порожденных нейросетевыми разложениями данных Коши и т.п.),
  • применение эволюционных алгоритмов и естественного распараллеливания задачи для одновременной настройки весов и структуры нейронных сетей подобно тому, как это делалось в работах авторов [6-7],
  • рассмотрение других подходов и соответствующих им алгоритмов при настройке нейросетевого функционального базиса, например, методов минимизации функционала ошибки, применявшихся в работах [9-10].

Литература

1. Васильев А.Н. Построение приближенных математических моделей распределенных систем на основе нейросетевой методологии// «Нейрокомпьютеры»: разработка, применение. – М.: Радиотехника, 2007. – №9. – С.103-116.

2. Васильев А.Н., Тархов Д.А. Нейронные сети как новый универсальный подход к численному решению задач математической физики // «Нейрокомпьютеры»: разработка, применение. – 2004. – №7-8. – С.111-118.

3. Васильев А.Н., Тархов Д.А. Применение нейронных сетей к неклассическим задачам математической физики// Сборник докладов Международной конференции по мягким вычислениям и измерениям – SCM'2003. – СПб., 2003. – Том 1. – С.337-340.

4. Самарский А.А., Вабищевич П.Н. Численные методы решения обратных задач математической физики. – М.: Едиториал УРСС, 2004. – 480 с.

5. Тархов Д.А. Нейронные сети: модели и алгоритмы. Кн.18. – М.: Радиотехника, 2005. – 256 с.

6. Васильев А.Н., Тархов Д.А. Некоторые эволюционные подходы к нейросетевому решению задач математической физики// Сборник научных трудов VIII Всероссийской научно-технической конференции «Нейроинформатика-2006». – Москва, МИФИ, 2006. – Часть 1. – С.24-31.

7. Васильев А.Н., Тархов Д.А. Эволюционные алгоритмы решения краевых задач в областях, допускающих декомпозицию (NPNJ-2006)// Математическое моделирование. – 2007. – Том 19, №12. – С.52-62.

8. Galperin E., Zheng Q., Solution and control of PDE via global optimization methods// Computers & Mathematics with Applications. – Pergamon Press Ltd. – 1993. – Vol. 25, No. 10/11. – pp. 103-118.

9. Galperin E.A., Kansa E.J. Application of global optimization and radial basis functions to numerical solutions of weakly singular Volterra integral equations// Computers & Mathematics with Applications. – Pergamon Press Ltd. – 2002. – Vol. 43. – pp. 491-499.

10. Galperin E.A. The Cubic Algorithm for Optimization and Control// NP Research Publ., Montreal. – 1990.