Geum.ru

Программа дисциплины «вычислительная математика» Индекс дисциплины по учебному плану: ен. Ф. 01. 4 Направление 230200 Информационные системы

Вид материалаПрограмма дисциплины

Содержание


Правильные ответы к тестам
Подобный материал:
1   2   3   4   5

в точке x=1 третье слагаемое получается равным:

1.1,80 2.2,75 3.1,75


5.10.На втором шаге решения методом Зейделя системы уравнений

x=1–0,5cos(y)

y=sin(x+1)–1,2 = 0

при начальном приближении x0=1 y0=1

получены приближенные значения x2=0,511 y2=–0,202

Укажите правильное утверждение

1.Значения обеих переменных найдены верно.

2.Значения обеих переменных найдены не верно.

3.Значение одной переменной найдено верно, а другой нет.


5.11.При разбиении отрезка интегрирования на 20 частей вычисление по пер­­вой формуле пря­моугольников дало значение интеграла, равное 32, а по фор­му­ле трапеций – равное 28. Вычисление по второй формуле пря­­моуголь­ни­­­ков даст значение:

1.36 2.30 3.24

ПРАВИЛЬНЫЕ ОТВЕТЫ К ТЕСТАМ
Номер теста

Задание
I
II
III
IV
V

1
1
2
3
1
2

2
3
2
1
2
1

3
2
1
1
3
3

4
3
1
2
2
4

5
1
3
3
1
2

6
2
3
2
3
1

7
2
1
2
2
1

8
3
3
3
3
2

9
4
2
1
1
3

10
2
3
1
1
1

11
1
1
2
2
3



12.Контрольные вопросы для оценки остаточных знаний.


1) Решить заданную систему из четырех линейных уравнений мето­да­ми Гаусса и Зейделя (с точностью до 0,1), например,

8x1–4x2+x3+x4 = – 23 5x2+4x3 = 14 x1+x2–3x3 = –3 x2–2x4 = 2

2)Найти любой корень уравнения f(x)=0 c точностью до 0,1 по оси ординат, например,

x3 + x + 1 = 0.

3)Вычислить приближенное значение определенного интеграла 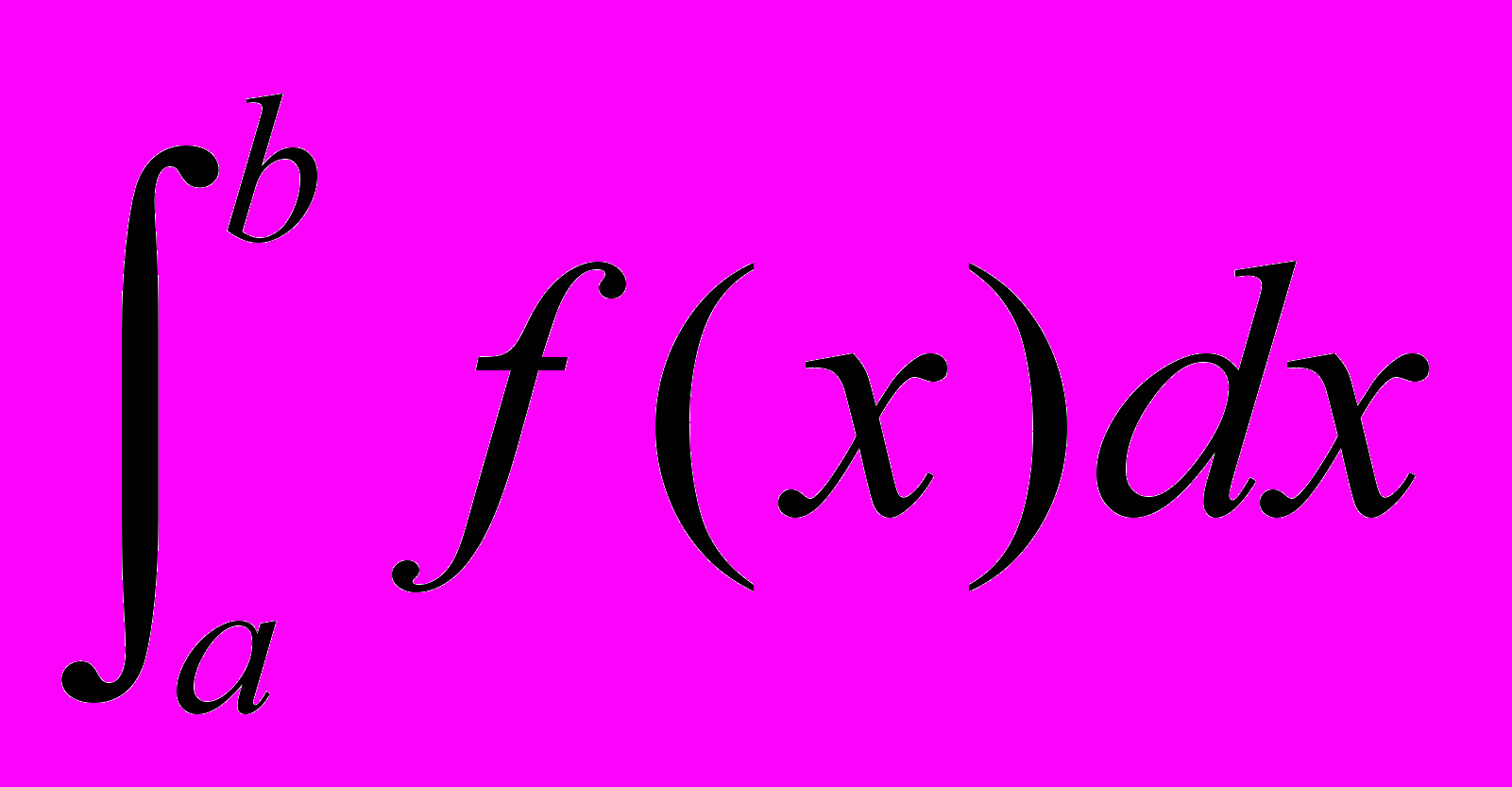, разбив отрезок интегрирования на 4 и 10 частей, например для f(x)= x4+3x–1, a= –3, b= –2

4)Используя Excel, построить по экспериментальным данным полиномы различ­­ных сте­пе­ней, аппрокси­ми­рующие зависимость y от x. Рассчитать ко­эф­фи­ци­енты полиномов и сум­мы квадратов невязок. Например,

X
1,10
1,20
1,40
1,60

Y
-0,879
-0,712
-0,216
0,536

5)Используя MathCAD, построить таблицы и графики, отражающие зави­си­мость корней системы уравнений x и y от правых частей: a (при b=0) и b (при a=0), например,

y–ex = a

x+y–2 = b


13.Учебно–методическое обеспечение дисциплины.

13.1.Рекомендуемая литература


а) основная литература:

1.Волков Е.А. Численные методы. Учебное посо­бие. – М: Наука, 1982. – 256 с.

2.Штейнберг А.М. Вычислительная математика. Методические указания к выполнению лабораторных работ. – Самара, СамГАСУ, 2006. – 16 с.


б) дополнительная литература:

1.Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.

2.Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. – СПб.:БХВ-Петербург, 2005. – 464 с.


14.Материально-техническое обеспечение дисциплины


Персональные компьютеры класса Pentium-233/RAM-32Мб/HDD-4Гб.


15.Программно-информационное обеспечение дисциплины


1)Табличный процессор Microsoft Excel.

2)Пакет программ MathCad.


16. Перечень используемых инновационных методов и разработок
  1. Электронная рабочая программа и журнал преподавателя в Интернет, разработанные на ка­федре.
  2. Рейтинговая система учета академической активности студентов при изучении дис­цип­ли­ны, разработанная на кафедре.
  3. Тестовая система ФИСТ.



17.Методические рекомендации преподавателю дисциплины

Основными видами обучения студентов являются лекции, лабораторные занятия в дис­плей­ном классе и самостоятельная работа студентов.

При чтении лекций особое внимание следует уделить выработке у студентов умения пе­­­реходить от абстрактной математической модели к конкретным алгоритмам, обес­пе­чи­ва­­ющим ее численную реализацию, доводить анализ до числовых результатов и со­дер­жа­тель­но интерпретировать эти результаты.

Лабораторный практикум ориентируется на реализацию алгоритмов вычислительной ма­те­матики, как с использованием стандартных средств, предоставляемых пакетами прог­рамм (Excel, MathCad), так и путем разработки собственных программ. Результаты каж­до­го занятия должны оформляться студентами в соответствии с требованиями, указанными в методических указаниях к лабораторным работам и сохраняться до завершения курса.

Самостоятельная работа заключается в предварительном изучении теоретического ма­териала, необходимого для выполнения лабораторных работ и программировании алго­рит­мов, реализующих указанный преподавателем численный метод. Оценка само­сто­я­тель­ной работы должна входить в оценку контрольных точек практикума с учётом кон­т­ро­ля остаточных знаний по тестовым вопросам.


18.Методические указания для студентов

Основными методами обучения являются лекции, лабораторные занятия в дисплейном классе и самостоятельная работа.

При прослушивании и проработке лекций особое внимание следует уделить тер­ми­нологии, используемой в дисциплине, логике реализации изучакмых численных ме­то­дов, обоснованию их результативности и оценке эффективности.

Необходимо помнить, что знание численного метода включает:

а)умение сформулировать постановку задачи, описать необходимые исходные данные и требуемый результат расчета;

б)навык пошагового выполнения алгоритма, например, в электронных алгоритмов;

в)умение составить блок–схему алгоритма метода и программу для его реализации на языке програм­ми­ро­ва­ния;

г)умение обосновать возможность применения алгоритма, условия его резуль­та­тив­нос­ти и эффективности.

При подготовке к лабораторному практикуму необходимо повторить теоретический ма­те­риал по теме предстоящей работы, завершить расчеты и их оформление по пре­ды­ду­щей работе. Если прошедшая работа включает задание на программирование, необходимо за­вер­шить разработку программы, выполнить тестирование, оформить программу и блок–схему.

Документирование и формирование итоговой отчётности следует начинать забла­го­вре­мен­но и вести в соответствии со стандартами оформления учебных документов и научно-ис­­следовательских отчётов. Без предоставления отчётов студенты не могут быть ат­тес­то­ва­ны по дисциплине в целом.

Важной частью промежуточной аттестации является контроль остаточных знаний, со­от­ветствующие вопросы следует попросить у преподавателя заранее и самостоятельно к ним подготовиться.