Программа дисциплины «вычислительная математика» Индекс дисциплины по учебному плану: ен. Ф. 01. 4 Направление 230200 Информационные системы

Вид материала

Программа дисциплины

Подобный материал:

• Программа дисциплины «информационные сети» Индекс дисциплины по учебному плану: опд., 123.28kb.
• Программа дисциплины «Дискретная математика» Индекс дисциплины по учебному плану ен., 194.02kb.
• Самостоятельная работа студентов 34 Курсовой проект. Форма итогового контроля: экзамен, 371.54kb.
• Программа дисциплины «Информационная безопасность и защита информации» Направление, 280.62kb.
• Рабочая программа учебной дисциплины дн. Ф. 13 Операционные системы Для направления, 227.68kb.
• Многоуровневая учебная программа дисциплины электротехника и электроника для подготовки, 409.29kb.
• Аннатационная программа дисциплины теория вероятностей, случайные процессы направление, 46.02kb.
• Рабочая программа дисциплины (указывается шифр и наименование дисциплины по учебному, 610.49kb.
• Программа дисциплины "Информационно-поисковые системы" Направление 230200 Информационные, 236.78kb.
• Рабочая программа дисциплины «офисное программирование» Индекс дисциплины по учебному, 133.25kb.

в точке x=2, слагаемое, соответствующее x₁, получается равным:

1. 4 2.–4 3.–3


2.10.На втором шаге решения методом простых итераций системы уравнений

x=1–0,5cos(y)

y=sin(x+1)–1,2 = 0

при начальном приближении x⁰=1 y⁰=1

получены приближенные значения x²=0,721 y²=–0,213

Укажите правильное утверждение

1.Значения обеих переменных найдены верно.

2.Значения обеих переменных найдены не верно.

3.Значение одной переменной найдено верно, а другой нет.


2.11.При разбиении отрезка интегрирования на 10 частей вычисление по фор­­му­ле пря­мо­у­голь­ников с центральной точкой дало значение интеграла, рав­ное 10, а по фор­му­ле трапе­ций – равное 7. Вычисление по формуле пара­бол при разбиении отрезка интегрирования на 20 частей даст значение:

1.9,0 2.8,5 3.8,0


ТЕСТ 3

3.1.Система линейных уравнений

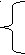8x₁ – 4x₂ + x₃ = 12

15x₁ – 9x₂ + 5x₃ = 21

x₁ + x₂ – 3x₃ = 3

1.Имеет единственное решение. 2.Не имеет решения.

3.Имеет множество решении


3.2.Систему линейных уравнений

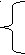12x₁ – 3x₂ + 4x₃ = 1

2x₁ –11x₂ + 6x₃ = 10

2x₁ + 8x₂ –1 2x₃ = –1

1.Можно решать методом простых итераций.

2.Нельзя решать методом простых итераций.

3.Можно решать методом простых итераций, переставив строки


3.3.На втором шаге решения методом простых итераций системы линейных уравнений

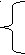4x₁ – x₂ + x₃ = 4

x₁ –5 x₂ + 2x₃ = –2

2x₁ + x₂ –4x₃ = –1

при начальном приближении x₁⁰=0 x₂⁰=2 x₃⁰=–1

получены значения x₁²=0.813 x₂²=1.050 x₃²=1.125

Укажите правильное утверждение

1.Значения всех переменных найдены верно.

2.Значения всех переменных найдены не верно.

3.Значения одних переменных найдены верно, а других нет.


3.4.Даны две матрицы A и B.



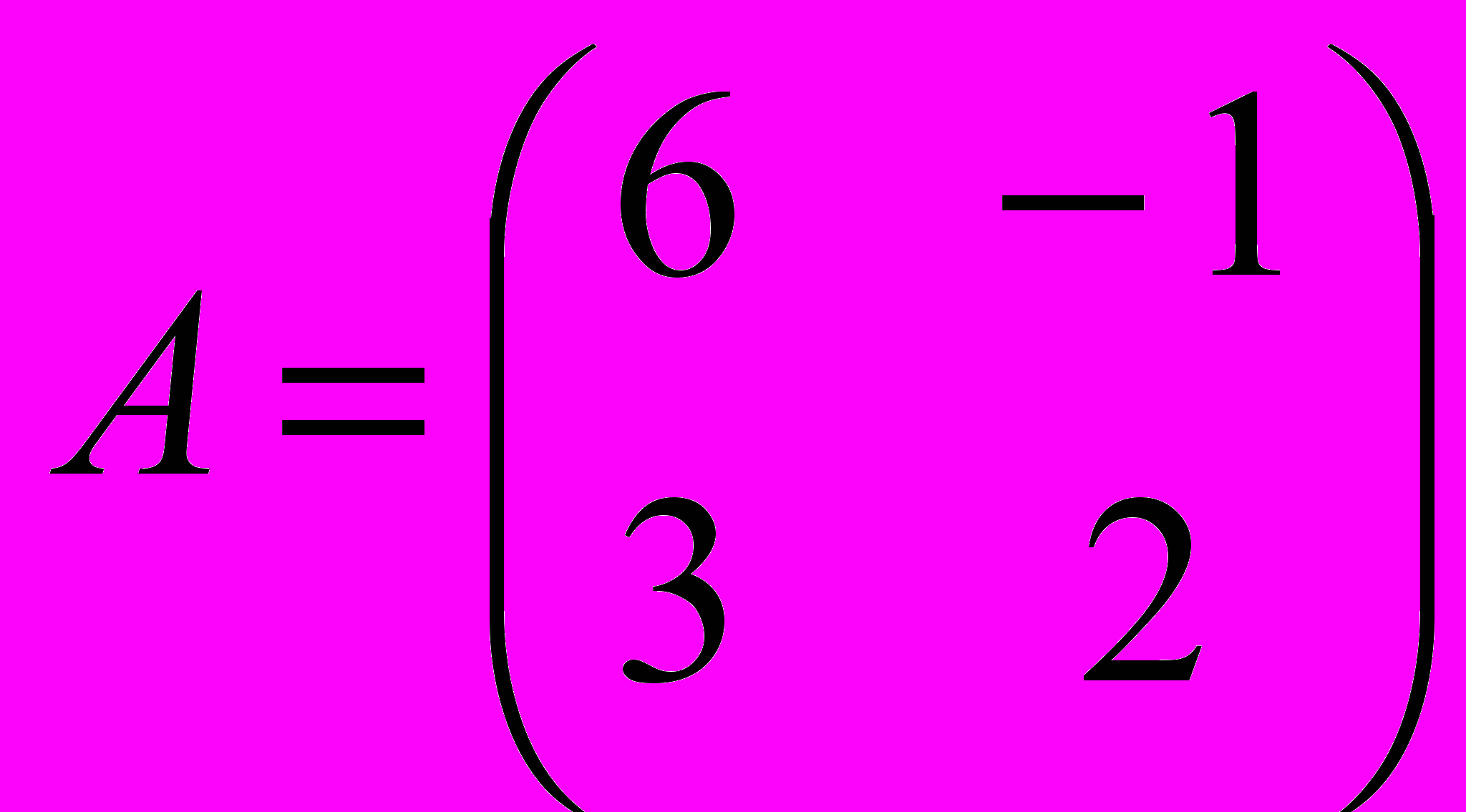
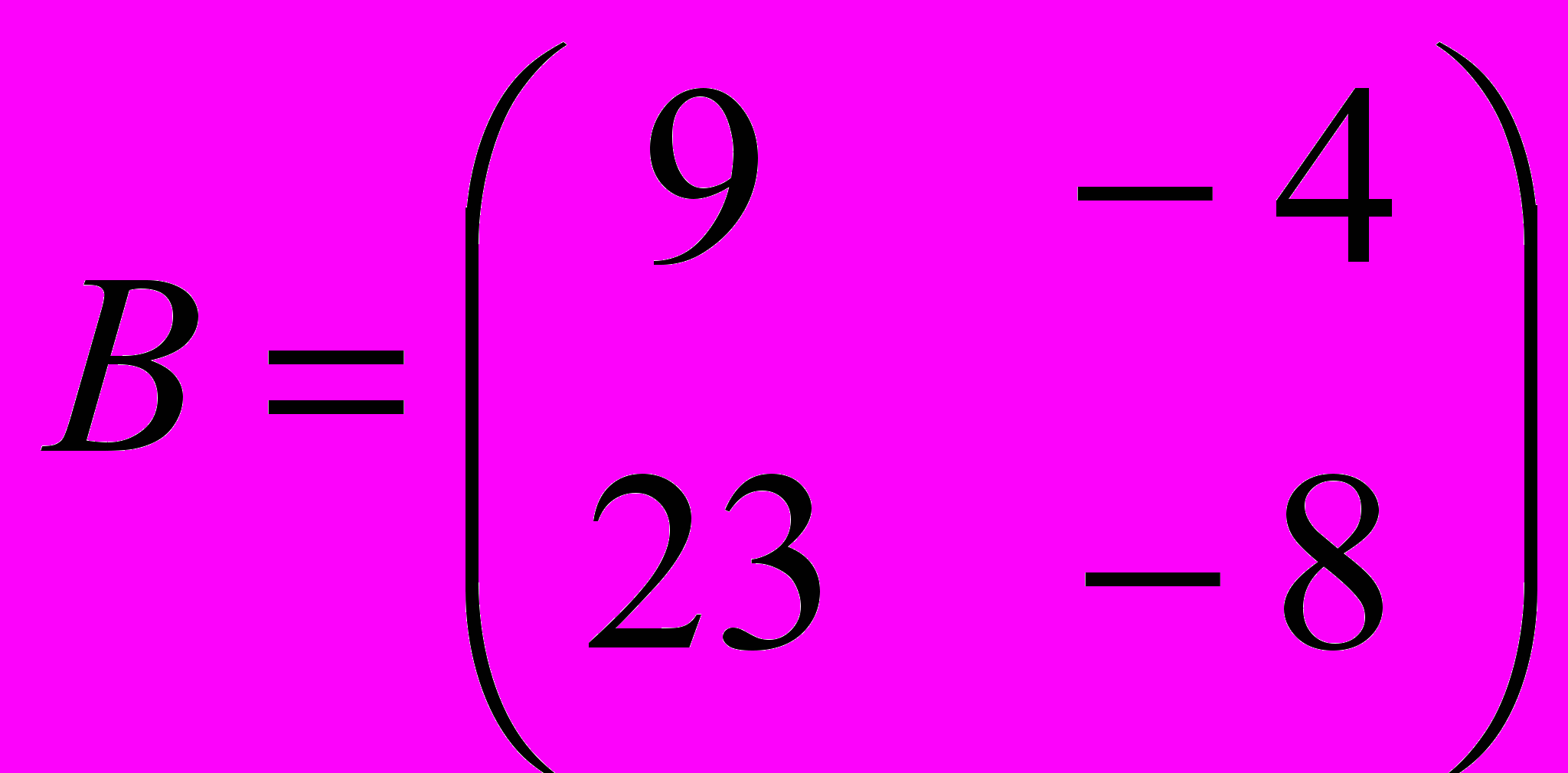
Число –4

1.Является собственным числом только матрицы A.

2.Является собственным числом только матрицы B.

3.Является собственным числом обеих матриц.

4.Не является собственным числом ни одной из этих матриц.


3.5.При уточнении корня уравнения x³+3x–1= 0 методом хорд на начальном отрезке [0;1] значение x=0,318 получается на

1.Первом шаге 2.Втором шаге 3Третьем шаге


3.6.Формула прямоугольников с центральной точкой дает точный ответ, если подинтегральная функция является полиномом

1.Не выше второй степени 2.Не выше первой степени

3.Не выше четвертой степени


3.7.При интегрировании функции f(x) методом прямоугольников с цент­раль­ной точкой на от­резке [1;3], если модуль второй призводной этой функ­ции не превышает 3, для дости­же­­ния точности 0,01 достаточно разбить отрезок ин­тег­ри­ро­ва­ния

1.На 8 частей 2.На 10 частей 3.На 12 частей


3.8.Какой из приведенных полиномов дает по критерию метода наимень­ших квадратов луч­­шую аппроксимацию эк­спе­­ри­мен­тальных данных

x	-2	0	2	3	4
y	-5	6	3	1	2

1.y=2x²–x+3 2.y=x²+2x–3 3.y=x²–2x+1


3.9.На первом шаге решения методом Ньютона системы уравнений

y–2e^x = 0

x+y–2 = 0

при начальном приближении x⁰=1 y⁰=1

получены значения x¹=0,311 y¹=1,689

Укажите правильное утверждение

1.Значения обеих переменных найдены верно.

2.Значения обеих переменных найдены не верно.

3.Значение одной переменной найдено верно, а другой нет.


3.10.Для таблично заданной функции

Номер точки	0	1	2	3	4
x	1	2	3	5	7
y	7	6	3	4	2

рас­считаны конечные разности различного порядка в точке x₀.

01	02	03	04
-1	-3	5	-12

Сколько из них рассчитано верно?


3.11.При разбиении отрезка интегрирования на 12 частей вычисление по вто­рой формуле пря­моугольников дало значение интеграла, равное 20, а по фор­­му­ле трапеций – равное 18. Вычисление по первой формуле пря­­моуголь­ни­ков даст значение:

1.22 2.16 3.19

ТЕСТ 4

4.1.Система линейных уравнений

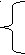7x₁ – 3x₂ + 2x₃ = 1

4x₂ + 5x₃ = 14

2x₁ + 3x₂ – 2x₃ = –1

1.Имеет единственное решение. 2.Не имеет решения.

3.Имеет множество решении


4.2.Систему линейных уравнений

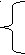2x₁ – 3x₂ + x₃ = 1

5x₁ – x₂ + 6x₃ = 10

2x₁ + 3x₂ – 2x₃ = –1

1.Можно решать методом простых итераций.

2.Нельзя решать методом простых итераций.

3.Можно решать методом простых итераций, переставив строки


4.3.На втором шаге решения методом Зейделя системы линейных уравнений

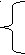4x₁ – x₂ + x₃ = 4

x₁ –5 x₂ + 2x₃ = –2

2x₁ + x₂ –4x₃ = –1

при начальном приближении x₁⁰=–1 x₂⁰=–1 x₃⁰=–1

получены значения x₁²=-0.750 x₂²=0.990 x₃²=0.798

Укажите правильное утверждение

1.Значения всех переменных найдены верно.

2.Значения всех переменных найдены не верно.

3.Значения одних переменных найдены верно, а других нет.


4.4.Даны две матрицы A и B.



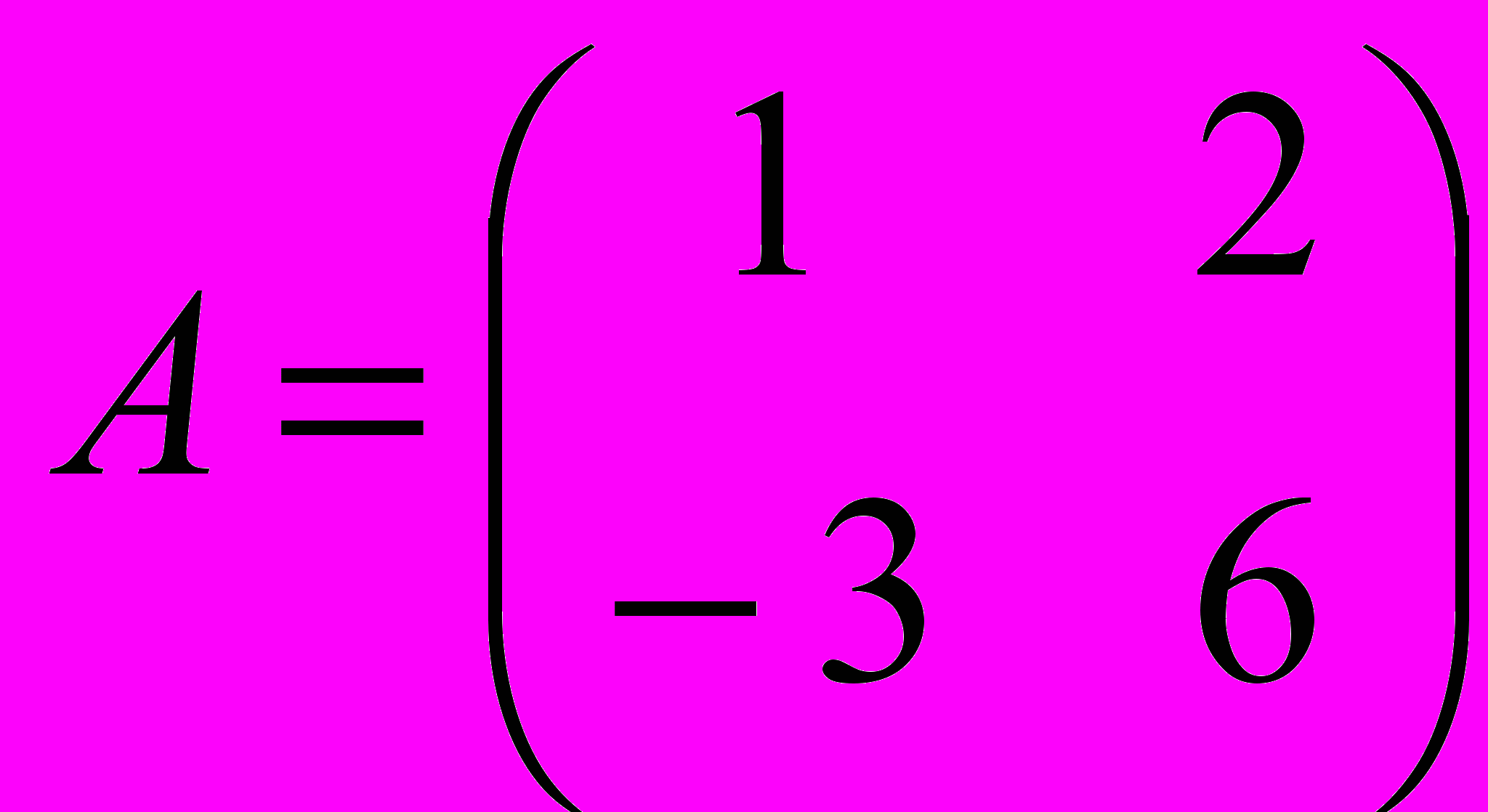
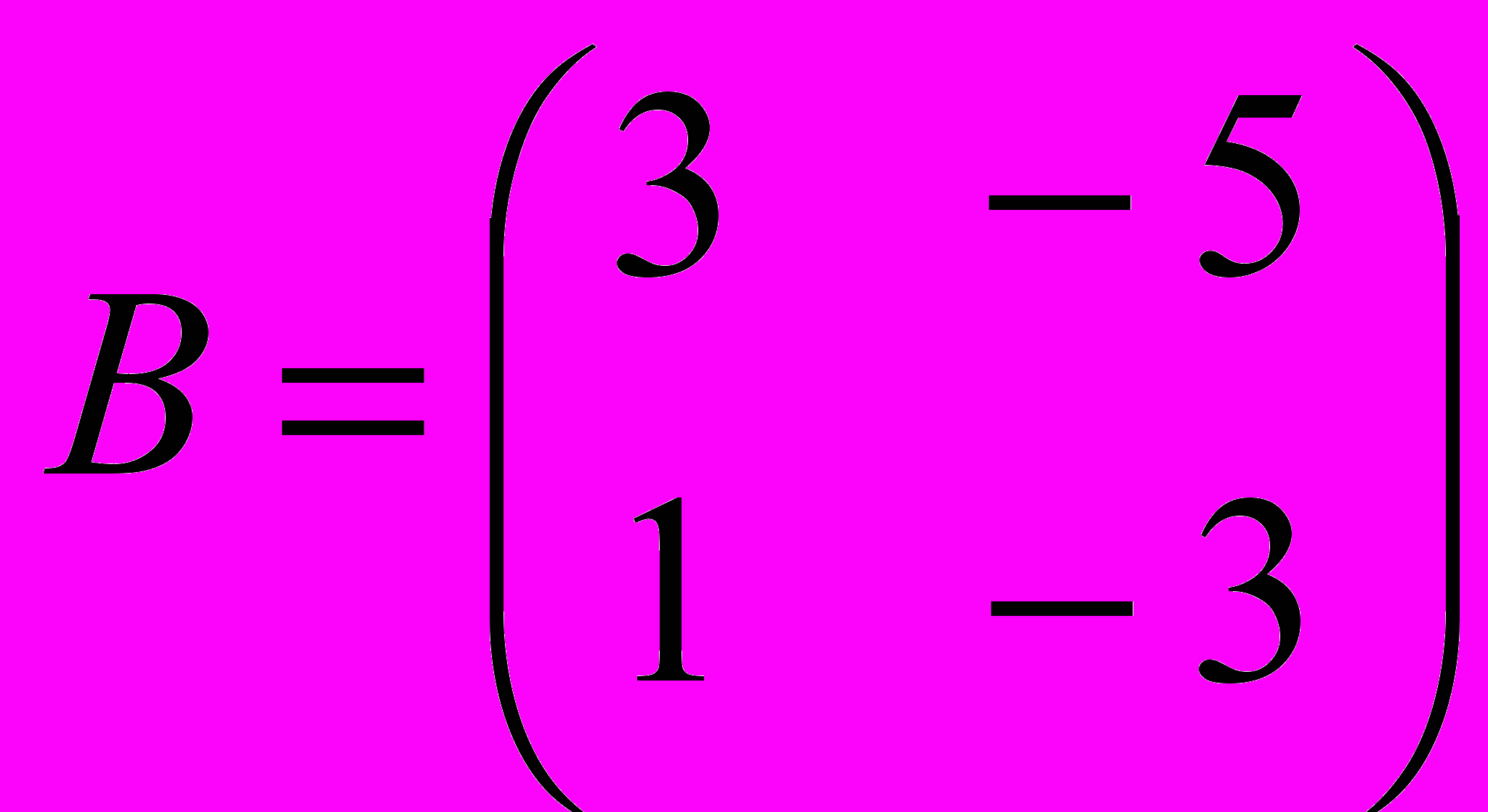
Вектор

1.Является собственным вектором только матрицы A.

2.Является собственным вектором только матрицы B.

3.Является собственным вектором обеих матриц.

4.Не является собственным вектором ни одной из этих матриц.


4.5.При уточнении корня уравнения x³+3x+5= 0 методом касательных на начальном от­рез­ке [-2;-1] значение x=-1,400 получается на

1.Первом шаге 2.Втором шаге 3.Третьем шаге


4.6.Формула трапеций дает точный ответ, если подинтегральная функция является поли­но­мом

1.Не выше второй степени 2.Не выше третьей степени

3.Не выше первой степени


4.7.При интегрировании функции f(x) методом трапеций на отрезке [1;4], если модуль вто­рой призводной этой функции не превышает 2, для достиже­ния точности 0,10 дос­та­точ­но разбить отрезок ин­тег­ри­ро­ва­ния

1.На 6 частей 2.На 8 частей 3.На 10 частей


4.8.Какой из приведенных полиномов дает по критерию метода наимень­ших квадратов луч­шую аппроксимацию эк­спе­­ри­мен­тальных данных

x	0	1	3	4	5
y	-5	6	3	1	2

1.y=2x²–x+3 2.y=x²+2x–3 3.y=x²–2x+1


4.9.При интерполяции полиномом Лагранжа данных таблицы

x	1	3	5	6
y	-5	6	3	1

в точке x=4, слагаемое, соответствующее x₁, получается равным:

1.–3 2.–2 3. 3


4.10.На втором шаге решения методом простых итераций системы уравнений

x=1–0,5cos(y)

y=sin(x+1)–1,2 = 0

при начальном приближении x⁰=1 y⁰=1

получены приближенные значения x²=0,521 y²=–0,213

Укажите правильное утверждение

1.Значения обеих переменных найдены верно.

2.Значения обеих переменных найдены не верно.

3.Значение одной переменной найдено верно, а другой нет.


4.11.При разбиении отрезка интегрирования на 10 частей вычисление по фор­­му­ле пря­мо­у­голь­ников с центральной точкой дало значение интеграла, рав­­ное 16, а по фор­му­ле тра­пе­ций – равное 13. Вычисление по формуле па­ра­­бол при разбиении отрезка интегрирования на 20 частей даст значения:

1.14,5 2.15,0 3.14,0

ТЕСТ 5

5.1.Система линейных уравнений

7x₁ – 3x₂ + 2x₃ = 1

12x₁ – 9x₂ + 6x₃ = 10

2x₁ + 3x₂ – 2x₃ = –1

1.Имеет единственное решение. 2.Не имеет решения.

3.Имеет множество решении


5.2.Систему линейных уравнений

10x₁ – 3x₂ + x₃ = 1

2x₁ –15 x₂ + 4x₃ = 10

2x₁ + 8x₂ –18x₃ = –1

1.Можно решать методом простых итераций.

2.Нельзя решать методом простых итераций.

3.Можно решать методом простых итераций, переставив строки


5.3.На втором шаге решения методом простых итераций системы линейных уравнений

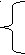4x₁ – x₂ + x₃ = 4

x₁ –5 x₂ + 2x₃ = –2

2x₁ + x₂ –4x₃ = –1

при начальном приближении x₁⁰=–1 x₂⁰=–1 x₃⁰=–1

получены значения x₁²=-0.925 x₂²=0.895 x₃²=1.888

Укажите правильное утверждение

1.Значения всех переменных найдены верно.

2.Значения всех переменных найдены не верно.

3.Значения одних переменных найдены верно, а других нет.


5.4.Даны две матрицы A и B.



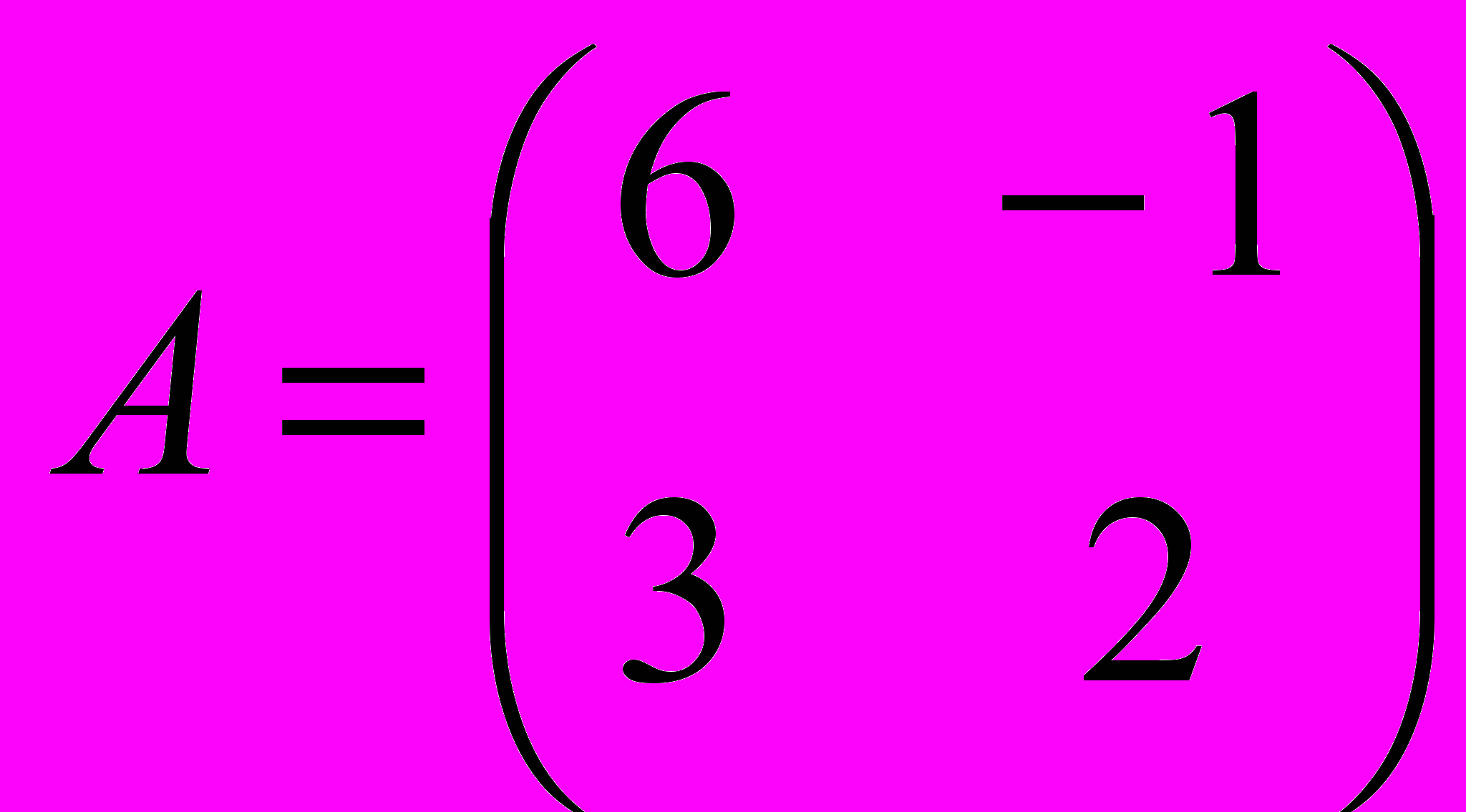
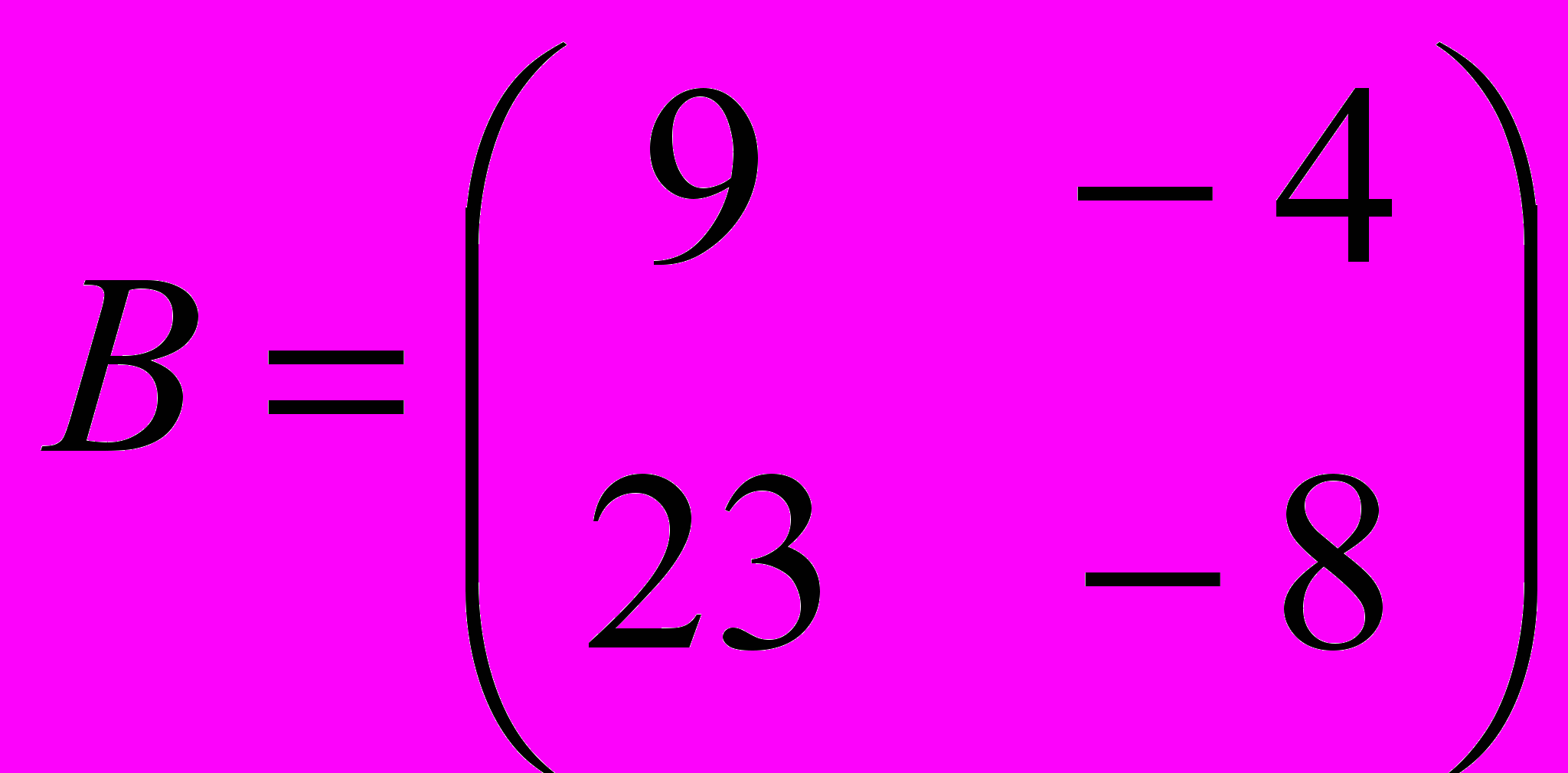
Число 6

1.Является собственным числом только матрицы A.

2.Является собственным числом только матрицы B.

3.Является собственным числом обеих матриц.

4.Не является собственным числом ни одной из этих матриц.


5.5.При уточнении корня уравнения x=x-(x³–2x+2)/20 методом итераций с на­чаль­ным при­ближением x⁰=–2 значение x=-1,847 получается на

1.Первом шаге 2.Втором шаге 3.Третьем шаге


5.6.Формула Симпсона дает точный ответ, если подинтегральная функция является полиномом

1.Не выше третьей степени 2.Не выше второй степени

3.Не выше первой степени

.

5.7.При интегрировании функции f(x) методом Симпсона на отрезке [-3;–1] при условии, что модуль четвертой призводной этой функции не превышает 10, для достижения точ­нос­ти 0,10 достаточно разбить отрезок ин­тег­ри­ро­ва­ния

1.На 6 частей 2.На 8 частей 3.На 10 частей


5.8.Какой из приведенных полиномов дает по критерию метода наимень­ших квадратов луч­шую аппроксимацию эк­спе­­ри­мен­тальных данных

x	-1	1	2	3	4
y	-5	6	3	1	2

1.y=2x²–x+3 2.y=x²+2x–3 3.y=2x²–2x+1


5.9.При интерполяции данных таблицы полиномом Ньютона

x	0	2	4	6
y	-5	6	3	1