Ббк 65. 290-26

Вид материала

Книга

Содержание Deutsche Telecom Heidelberger Druckmaschine Energie Baden Wueit. САРМ, нам нужно знать три параметра — r Источник оценки: Credit Suisse First Boston (Europe) Limited (CSFB). 4.2. Расчет стоимости капитала Merril Lynch, Beta Box, Bloomberg, Value Line Financial Times D рыночную стоимость заемных средств, за Е —

Подобный материал:

• Отдел комплексного страхования Тел.: (095) 290-7703, 290-8199. Факс: (095) 290-8199, 23.5kb.
• Учебно-методическое пособие Нижний Новгород 2010 удк 338. 24(075. 8) Ббк 65. 290-2я73, 2121.39kb.
• Програма навчальної дисципліни Менеджмент Острог, 2006 удк 338. 23 (075. 8) Ббк 65., 203.38kb.
• Cols=2 gutter=490> ббк 65. 290-5 Ф32, 558.99kb.
• Краткий курс филип котлер издательский дом "вильямс" Москва Санкт-Петербург Киев 2007, 18994.02kb.
• Удк 339. 138(075. 8) Ббк 65. 290-2, 658.5kb.
• В. Земских I Редактор Н. Дмитревская Художественный редактор в земских Верстка В. Зассеева, 3925.27kb.
• Преимущества фир мы ОАО «Типография «новости» Москва 2000 удк 334. 722: 339. 137 Ббк, 4912.01kb.
• Обвинительное заключение, 2936.93kb.
• Верстка Е. Строганова И. Андреева Е. Базанов Е. Маспова С. Жильцов, А. Калабин Е. Базанов, 4179.01kb.

Ряд САРМ 31/12/98	Компания	Бета	Источник	Ряд САРМ 31/12/98	Компания	Бега	Источник
1	Deutsche Telecom	0,974	Рассчитано	16	Schering	0,882	DS
2	SAP	1,014	DS	17	Lufthansa	1,124	DS
3	Mannesmann	1,263	DS	18	Preussag	0,909	DS
4	Daimler-Benz	1,148	DS	19	Thyssen	0,981	DS
5	Siemens	1,094	DS	20	Beierdorf	0,83	DS
6	RWE	0,847	DS	21	Fresenius Medical Care	0,72	Рассчитано
7	Bayer	1,059	DS	22	Heidelberger Druckmaschine	0,698	Рассчитано
8	Veba	0,813	DS	23	Linde	0,895	DS
9	Volkswagen	1,270	DS	24	Degussa	1,244	DS
10	Metro	0,445	Рассчитано	25	GEHE	0,394	DS
11	Hoechst	1,04	DS	26	Adidas Salomon AG	0,912	Рассчитано
12	BASF	1,043	DS	27	Mobilcom	0,679	Рассчитало
13	BMW	1,328	DS	28	Energie Baden Wueit.	0,168	DS
14	Viag	0,681	DS	29	Lahmeyer AG	0,698	DS
15	Henkel	1,112	DS	30	Karstadt	0,577	DS

• Суммарный риск = несистематический риск (риск, характер-­
  ный для данной фирмы) + систематический риск (рыночный
  риск, или (β -риск).
  
• Примерами несистематического риска являются: смерть генераль­-
  ного директора, забастовка в компании, неудача проекта в сфере ис­
  следований и разработок и т. п.
  
• При анализе риска в расчет принимается не изменчивость сама
  по себе (среднеквадратическое отклонение доходности акций),
  а корреляция доходности фирмы и средней доходности рынка.
  Коэффициент β измеряет риск, оставшийся после того, как пор­-
  тфель инвестиций был диверсифицирован.
  

♦ Инвесторы не получают компенсацию за риск, который они мо­гут избежать. Риск, за который они должны получать компенса­цию, это систематический (β) риск.

4.1.2. Применение САРМрря измерения ожидаемой доходности

САРМ устанавливает простое линейное соотношение между риском и доходностью¹:

¹ Целью данной книги не является подробное изложение САРМ и тех допу­щений, на которых основывается эта модель. Такую информацию можно най­ти в любом теоретическом источнике, представляющем модель оценки доход­ности финансовых активов.


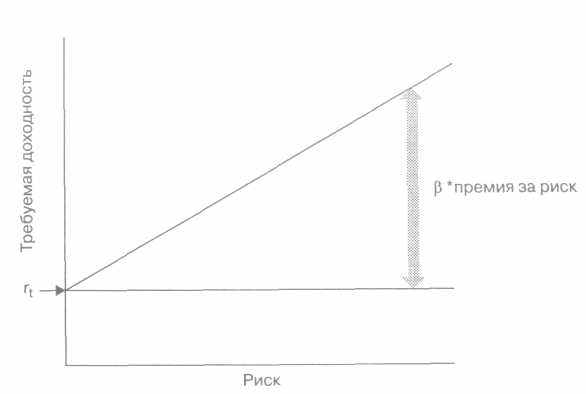
140


Рис. 4.3. Соотношение между риском и доходностью

E(R) = r_f+ β (r_m-r_f),

где E(R) — доходность, ожидаемая инвесторами, г,— норма безриско­вой доходности, β (r_m - r_f) — премия за риск, необходимая инвесторам и состоящая из:

• r_m - r_f — премии за риск рынка капитала, т. е. доходности, ожи­
  даемой для хорошо диверсифицированного рыночного портфе­
  ля сверх безрисковой нормы доходности. Эта составляющая пред­
  ставляет собой «цену риска».
  
• β — меры «степени риска».
  

При нулевом уровне риска инвесторы предполагают заработать без­рисковую норму прибыли — r_f.

При более высоком уровне риска инвесторы надеются получить в до­полнение к безрисковой норме прибыли некоторую премию за риск, которая зависит от средней премии за риск, ожидаемой на рынке, и ве­личины риска, которую берут на себя инвесторы. Рисунок 4.3 демонст­рирует простое линейное соотношение между риском и доходностью.

Для того чтобы оценить составляющие модели САРМ, нам нужно знать три параметра — r_f, β и (r_m-r_f):

♦ r_f — это доходность государственных облигаций со сроками погаше­
ния, приблизительно эквивалентными скорости оборота денежных

Т
141
аблица 4.4. Стоимость капитала в Европе (% на закрытие 04/02/99)

	Внутренняя норма доходности	Доходность 10-летних облигаций	Премия за риск	Откорректированный коэффициент изменчивости	Откорректированная премия за риск
Австрия	10,3	3,9	6,4	1,35	8,6
Бельгия	8,9	4,0	4,9	0,99	4,9
Дания	8,9	4,2	4,7	1,04	4,9
Финляндия	9,7	4,0	5,7	1,00	5,7
Франция	9,1	3,9	5,2	1,00	5,2
Германия	9,0	3,8	5,3	0,97	5,1
Ирландия	10,0	4,0	6,0	1,20	7,2
Италия	11,2	4,2	6,9	1,20	8,3
Нидерланды	9,1	3,9	5,2	0,80	4,2
Норвегия	11,5	4,8	6,7	1.05	7,0
Португалия	10,8	4,3	6,5	1,20	7,8
Испания	9,2	4,0	5,2	1,07	5,6
Швеция	9,9	4,1	5,8	0,98	5,6
Швейцария	9,0	2,5	6,5	0,87	5,7
Соединенное Королевство	10,5	4,2	6,2	0,72	4,5
Средневзвешенная			5,8		5,3

Источник оценки: Credit Suisse First Boston (Europe) Limited (CSFB).

средств, потоки которых оцениваются. Поэтому долгосрочные став­ки по казначейским ценным бумагам будут всегда выше, чем крат­косрочные.

♦ β — для того чтобы определить β, мы можем использовать линей­ную регрессию премии по данной акции (r_it-r_ft) на рыночную премию доходности (r_mt-r_ft). Здесь r_it представляет доходность ак­ций i в момент времени t; r_ft — это норма доходности, свободная от риска в момент времени t; а r_mt — норма на рынке в момент времени t. Но лучше не будем изобретать «велосипед», а вместо

э
142
того воспользуемся многочисленными источниками информа­ции, приводящими коэффициенты бета¹.

♦ (r_m-r_f) — это премия за риск рынка капитала, оцениваемая с помо­щью исторических данных. В отличие от безрисковой ставки пре­мия за риск довольно устойчива с течением времени. Таблица 4.4 показывает рыночную премию за риск для различных стран Ев­ропы со средним значением около 6%. Величина рыночной пре­мии за риск широко обсуждается на теоретическом уровне и во все большей степени находится в центре внимания инвестицион­ных банков, экономических консультантов и журналистов, пи­шущих на финансовую тематику².

4.2. Расчет стоимости капитала

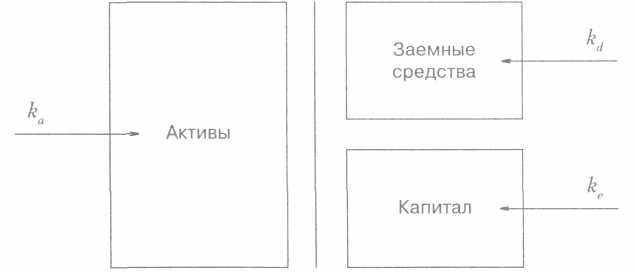
Стоимость капитала вытекает из базового линейного соотношения между риском и доходностью, которое мы только что рассмотрели. Мы можем посмотреть на него с двух сторон, в зависимости от того, на ка­кой стороне баланса мы сделаем акцент.



Стоимость долга k_d равна r_{f +} β_d * (r_m-r_f)

¹ Эти коэффициенты можно найти для американских компаний США через
Merril Lynch, Beta Box, Bloomberg, Value Line и многие другие источники. В Ев­
ропе среди других источников коэффициенты бета можно найти, например,
у Datastream, Barra International, Associes en France.

² Cm. «Wall Street and the amazing vanishing risk premium», Financial Times, 22
Apr. 1998; «Risk Premium Paradox», Financial Times, 15 June 1998; «Calculated
Risks», Financial Times, 3 May 1999.

Э
143
то ожидаемая ставка доходности, которую требуют инвесторы, пре­доставляющие фирме заемные средства. Стоимость акционерного капитала k_e равна

r_{f +} β_e * (r_m-r_f)

Это ожидаемая ставка доходности держателей акционерного капита­ла для того, чтобы компенсировать стоимость упущенных возможно­стей и риски.

Рентабельность активов k_a равна

r_{f +} β_a * (r_m-r_f)

Это ожидаемая норма прибыли, которую должна получать компания для того, чтобы удовлетворить требования всех инвесторов (предо­ставляющих как заемный, так и собственный капитал).

Если мы обозначим за D рыночную стоимость заемных средств, за Е — рыночную стоимость акционерного капитала и за V— суммарную рыночную стоимость фирмы, очевидно, мы должны получить следую­щее соотношение:

k_a = D/V*k_d + E/V*k_e. (1)

Учитывая то, что r_f и (r_m-r_f)одинаковы для этих трех стоимостей, мы можем прийти к следующей формуле:

β_a = D/V* β_d + E/V*β_e. (2)

Другими словами, β активов является средневзвешенной величиной β обязательств и β собственного капитала.

На практике, считая, что β_d довольно мала, мы пренебрегаем ею, и это позволяет нам упростить уравнение (2) следующим образом:

β_a = E/V*β_e (3)

Отметим, что бетой активов β_a иногда называют бету фирмы, не ис­пользующей рычага (левериджа) (unlevered). Ее иногда обозначают в расчетах β_u. Коэффициентом β акционерного капитала (β_e), соответ­ственно, называют бету фирмы, использующей рычаг (levered) и об­означают как β_l Вообще, расчет беты требует учета соотношения между рыночной стоимостью акционерного капитала и стоимостью фирмы¹. Когда у компании нет заемных средств, т. е. она не подвержена воз­действию рычага, бета активов, очевидно, равна бете собственного

¹ Часто структура капитала предоставляется с точки зрения учетной стоимо­сти. В большинстве случаев учетная стоимость обязательств равна их рыноч­ной стоимости, но это не так для акционерного капитала.

U
144
= означает отсутствие рычага (unlevered) L = означает наличие рычага (levered) A = активы
Е = акционерный капитал D = заемный каптал

Вu=В_А B_L=B_E

B_A=(E/V) B_E=(D/V) B_E« Bu=(D/V) B_D=(D/V) B_L

Заметьте, что когда Во = 0, эти выражения упрощаются до известных нам формул с приложением и без приложения рычага:

B_a=(E/V)B_eoBu = (E/V)Bl

К_и = R_F + В_и (R_M + R_F) о Кд =R_F + B_A (R_M + R_F)

К_и = D/V K_D + E/V К_Е, что подобно WACCA без налоговой защиты

Рис. 4.4. Терминология и математические соотношения

капитала. Вся эта терминология и математические соотношения све­дены воедино на рис. 4.4.

Проиллюстрируем все эти соотношения на простом примере. Ком­пания X имеет следующий баланс (в миллионах €) по рыночной сто­имости:



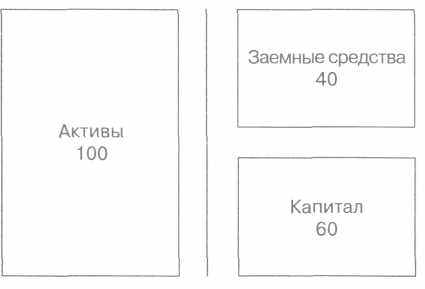
R_f равна 5%, и рыночная премия по акционерному капиталу считается равной 6%. Компания X имеет β акционерного капитала 1,3 и берет деньги в долг по ставке r_f, (это означает, что ее заемный капитал не подвержен риску и (β_d = 0).

Тогда стоимость акционерного капитала &_е равна 5% + 1,3x6% = 12,8%.

«
145
Смешанная» стоимость капитала':

D/Vxk_d + E/Vxk_e, следовательно, будет равняться

40% х 5% + 60% х 12,8% = 9,68%.

Исключая воздействие рычага на b акционерного капитала и при­меняя уравнение (3), мы можем найти b активов:

β _а= E/Vх β_e => 60% х 1,3 = 0,78. Рентабельность активов k_a равна

К _а ^{= r}/^{+ b}a^x (^r_m - ^r_f) ⁼ 5% + 0,78 (6%) = 9,68%.