Ббк 65. 290-26

Вид материала

Книга

Содержание Приложение ЗВ. Взаимосвязь между ROE EBIAT— проценты, очищенные от налогов. (3) Отмечаем, что проценты, очищенные от налогов, — это г EBIAT/ активы - г х D / А. R01 какой-то компании может быть рассмотрено как средневзвешен­ное отдачи двух гипотетических видов активов, идентичных ROA. ROI может быть выражен как ROI ROE, и результатом будет вышеприведенное уравнение (1), где ROE = ROA (ROA - i) D / E. 4.1.1. Определение и измерение риска Glaxo Wellcome British Telecom Vodafone Group Unilever (UK) Railtrack Group Rentokil Initial Marks & Spencei France Telecom Vivendi (ex Ge-nerde des Eaux) Elf Aquitaine Suez Lyonnaise lies Eaux Alcatel Alsthom Pinault Printemps ... Полное содержание

Подобный материал:

• Отдел комплексного страхования Тел.: (095) 290-7703, 290-8199. Факс: (095) 290-8199, 23.5kb.
• Учебно-методическое пособие Нижний Новгород 2010 удк 338. 24(075. 8) Ббк 65. 290-2я73, 2121.39kb.
• Програма навчальної дисципліни Менеджмент Острог, 2006 удк 338. 23 (075. 8) Ббк 65., 203.38kb.
• Cols=2 gutter=490> ббк 65. 290-5 Ф32, 558.99kb.
• Краткий курс филип котлер издательский дом "вильямс" Москва Санкт-Петербург Киев 2007, 18994.02kb.
• Удк 339. 138(075. 8) Ббк 65. 290-2, 658.5kb.
• В. Земских I Редактор Н. Дмитревская Художественный редактор в земских Верстка В. Зассеева, 3925.27kb.
• Преимущества фир мы ОАО «Типография «новости» Москва 2000 удк 334. 722: 339. 137 Ббк, 4912.01kb.
• Обвинительное заключение, 2936.93kb.
• Верстка Е. Строганова И. Андреева Е. Базанов Е. Маспова С. Жильцов, А. Калабин Е. Базанов, 4179.01kb.

Приложение ЗВ. Взаимосвязь между ROE и R0A

ROA не зависит от финансирования, и его связь с ROE показана в (1):
ROE=ROA (ROA - i) D/E, (1)

где i — процентная ставка после оплаты процентов по долгам. Доказательство для (1) приведено ниже. Даны два тождества (2) и (3).

а
132
ктивы = обязательства + собственный капитал; (2)

прибыль = EBIAT— проценты, очищенные от налогов. (3)

Отмечаем, что проценты, очищенные от налогов, — это г г Д т. е. (3) можно записать так:

прибыль = EBIA T-ixD. (4)

Разделим (4) на активы (Л):

прибыль / активы = EBIAT/ активы - г х D / А. (5)

Эти отношения были определены как

ROI=ROA-ixD/A. (6)

Напомним, что RO1, умноженное на леверидж (А / Е), равно ROE. Умножим (6) на А/Е:

ROE=ROAxA/E-ixD/AxA/E. (7)

Исходя из (2) А / Е = D / Е + 1 Подставляем

ROE=-ROAx(D/E+1)-i xD/E. (8)

Отсюда

ROE = ROA + (ROA -i)D / E. (9)

К этому результату можно прийти напрямую интуитивно.

R01 какой-то компании может быть рассмотрено как средневзвешен­ное отдачи двух гипотетических видов активов, идентичных ROA. Один из них на 100% финансируется за счет собственного капитала, а дру­гой — на 100% за счет обязательств. Активы, которые финансируются за счет собственного капитала, не несут бремени процентов, которые по­рождены целиком активами, финансируемыми за счет заемных средств.

Таким образом, ROI может быть выражен как

ROI = Е / А х ROA + D / A (ROA - i).

Это иллюстрирует взвешивание рентабельности двух видов акти­вов. Умножьте на леверидж, чтобы прийти к ROE, и результатом будет вышеприведенное уравнение (1), где

ROE = ROA (ROA - i) D / E.

Ч
133
АСТЬ II

ОЦЕНКА

Г
134
лава 4

СТОИМОСТЬ КАПИТАЛА: ПОНЯТИЕ И ОЦЕНКА

Одним из основных параметров финансирования является стоимость финансовых ресурсов, используемых фирмой. Деньги являются един­ственным столь распространенным «ресурсом», который задействует любое предприятие в любой отрасли. Понимание и оценка этого «това­ра широкого потребления» является важнейшим для любого руково­дителя, независимо от направления его работы. С точки зрения руко­водителей, стоимость денег, капитала — это только стоимость одного из ресурсов, она является одинаковой и для капитала, и для зарплаты сотрудников. С позиций инвесторов стоимость капитала компенсирует им риск и издержки неиспользованных возможностей, которые они мог­ли бы реализовать, вложив капитал в другие сопоставимые проекты.

4.1 Размышления о риске и доходности: беглый обзор модели оценки доходности финансовых активов (САРМ¹)

4.1.1. Определение и измерение риска

Инвесторам нужен некоторый доход от рыночной стоимости их ка­питальных вложений, соизмеримый с риском, который они не могут устранить с помощью диверсификации.

Рассмотрим два вида рисков: риск того, что смерч разрушит произ­водственные мощности компании А, и риск, связанный с тем, что вне­запный и резкий рост цены на нефть увеличит себестоимость продук­ции во всех отраслях хозяйства. Первый вид риска — несистематический, ограниченный и, следовательно, поддающийся диверсификации. Возможно,

САРМ — Capital Assets Pricing Model. — Прим. перев.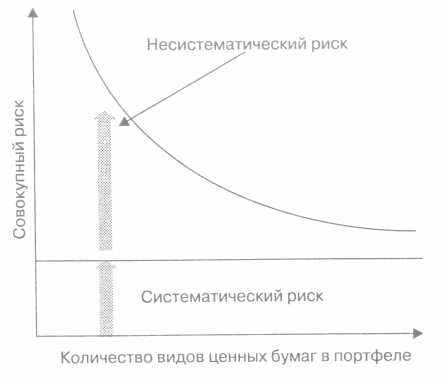


135


Рис. 4.1. Размышления о рисках

смерч разрушит завод компании А, но не разрушит завод компании В. Если мы владеем акциями обеих компаний, мы будем частично защи­щены от негативных явлений и событий, затрагивающих отдельные фирмы, но не влияющих на остальные, такие как смерчи. Второй вид риска является систематическим, не поддающимся диверсификации, поскольку рост цен на нефть будет оказывать неблагоприятное воздей­ствие на все предприятия (за исключением производителей нефти). Поэтому у нас не будет более надежной защиты от этого вида риска, даже если мы вложим деньги в акции как компании А, так и компании В, а не только в компанию А.

Следовательно, мы можем диверсифицировать несистематический риск, вкладывая деньги в несколько различных предприятий (эмпи­рические исследования показывают, что портфель инвестиций, вклю­чающий от 20 до 30 различных видов ценных бумаг, обладает очень низким несистематическим риском). Но мы не можем устранить с по­мощью диверсификации систематический риск, поскольку, по опре­делению, он оказывает воздействие на все предприятия. Это показано на рис. 4.1.

На финансовых рынках инвесторы получают вознаграждение за под­верженность только систематическому риску, поскольку это единственный вид риска, который они не могут избежать с помощью диверсификации.

Т
137

136
аблица 4.1. Коэффициенты β для некоторых британских компаний



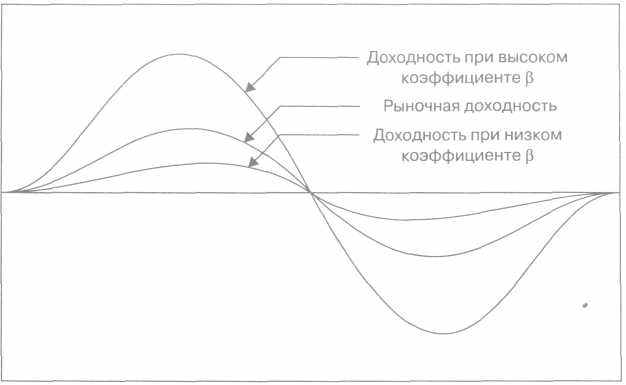
Рис. 4.2. Сводка доходности при различных коэффициентах бета

Методом, с помощью которого измеряют систематический риск, яв­ляется оценка ковариации доходности активов некоторой компании и рыночной доходности. Коэффициент β измеряет систематический риск, оценивая ковариацию доходности данной фирмы и средней ры­ночной доходности¹.

Компания, доходность которой в точности равна доходности рын­ка, является точно настолько же рискованной, как и рынок в целом; она имеет бету, равную единице².

¹ Коэффициент бета возникает при регрессии доходности фирмы на рыноч­
ную доходность. Таким образом, оценка Р равна

β _i = cov (r _i, r _m)/var (r _m )= σ²_i,т/ σ ²_т =ρ_{i, m} * σ_i * σ_т / σ²_т

где r _i = доходность компании i; r_т = рыночная доходность;

σ²_i,т = ковариация доходности фирмы с рыночной доходностью; σ_i = среднеквадратическое отклонение доходности компании г; σ_т = среднеквадратическое отклонение доходности рынка; ρ_{i, m} = коэффициент корреляции между доходностью фирмы и доходностью рынка.

² Математически, если доходности рассматриваемой фирмы и рынка совпа­
дают, то cov (r _i, r _m) = var (r _m), т. е. β = var (r_m)/var (r_m) = 1.

Ряд САРМ 31/12/98	Компания	Бета	Источник	Ряд САРМ 31/12/98	Компания	Бета	Источник
1	Glaxo Wellcome	0,88	DS (Datastieam)	16	Granada Group	1,14	DS
2	British Telecom	0,79	DS	17	Boots	0,51	DS
3	BP Amaco	0,65	DS	18	Cadbury Schweppes	0,98	DS
4	Smithkline-Beecham	1,10	DS	19	Sainsbury (J)	0,19	DS
5	Shell Tran­sport & T	0,85	DS	20	British Aerospace	1,22	DS
6	Vodafone Group	1,19	DS	21	Reuters Group	1,16	DS
7	Zeneca	0,94	DS	22	Kingfisher	0,59	DS
8	Diageo	1,04	DS	23	Orange	1,05	DS
9	Unilever (UK)	0,97	DS	24	British Ame­rican Tobacco	0,69	DS
10	Cable & Wireless	1,35	DS	25	Cable & Wireless CC	0,79	Рассчитано
11	BG	0,56	DS	26	Railtrack Group	0,41	DS
12	General Electric	0,81	DS	27	British Sky Broadcasting	0,42	DS
13	Rentokil Initial	1,13	DS	28	BAA	0,97	DS
14	Marks & Spencei	0,58	DS	29	Rio Tinto	0,77	DS
15	Tesco	0,58	DS	30	Scotish Power	0,75	DS

Любая компания, колебания, доходности которой превосходят сред­нюю рыночную доходность, является более рискованной и имеет ко­эффициент бета больше 1.

Компания же, чья доходность меняется меньше, чем рыночная доход­ность, является менее рискованной и имеет коэффициент бета меньше 1. Рисунок 4.2 иллюстрирует эти три случая, а в табл. 4.1-4.3 приведены примеры коэффициентов бета, рассчитанных для предприятий в Со­единенном Королевстве, Франции и Германии.

Обобщим ключевые моменты этого анализа:


Т
138
аблица 4.2. Коэффициенты β для некоторых французских компаний

Т
139
аблица 4.3. Коэффициенты β для некоторых немецких компаний

Ряд САРМ 31/12/98	Компания	Бега	Источник	Ряд САРМ 31/12/98	Компания	Бега	Источник
1	France Telecom	1,500	DS	16	Saint Gobain	1,069	DS
2	L 'Oreal	1,229	DS	17	Stmicro-electronics	0,591	DS
3	Vivendi (ex Ge-nerde des Eaux)	0,966	DS	18	Cap Gemini	0,770	DS
4	Elf Aquitaine	0,654	DS	19	Renault	1,488	DS
5	Suez Lyonnaise lies Eaux	0,923	DS	20	Synthelabo	0,397	DS
6	Carrefour	0,762	DS	21	Lafarge	0,985	DS
7	Total	0,508	DS	22	Schneider	1,448	DS
8	Alcatel Alsthom	1,438	DS	23	Canal +	0,425	DS
9	Pinault Printemps	1,108	DS	24	Hams (приобре­тена в мае 1998)	0,891	DS
10	Danone	0,930	DS	25	Accor	1,056	DS
11	Phone Poulenc	1,140	DS	26	Peugeot SA	1,091	DS
12	Sanofi	0,489	DS	27	Casino Guipchn.	0,611	DS
13	LVMH	1,163	DS	28	Sodexho Alliance	0,272	DS
14	Air Liquide	0,673	DS	29	Thomson-CSF	1,094	DS
15	Promodes	0,900	DS	30	Valeo	1,168	DS