1 блок (общие вопросы для всех специализаций)

Вид материала

Документы

Содержание Раздел «Экономико-математическое моделирование» 2) При помощи разработки линейного уравнения регрессии: Пример Линейная модель прибыли PR£0. Производство не является прибыльным при любом количестве изделий. б) Квадратичная модель затрат Маргинальными издержками При анализе по объему производства возможны три случая Геометрическая интерпретация ОЗ линейного программирования. Прибыль = 46,3 руб. Мультипликатор открытой экономики Мультипликатор открытой экономики

Подобный материал:

• Общие предметы для всех специализаций, 80.64kb.
• Методические указания к выполнению курсовых работ для всех специализаций специальности, 321.81kb.
• Контрольные вопросы по дисциплине «модели и алгоритмы обработки информации», 27.51kb.
• Программа учебной дисциплины дс. Р. 1 "Оценка недвижимости" Специальность 080105 «Финансы, 338.03kb.
• Методические указания к изучению курса «Политология» для студентов всех специальностей, 494.61kb.
• А. В. Гущин > Т. В. Гончаренко > А. Ю. Клыбин Итоговая аттестация диплом, 749.17kb.
• Учебно-методическое пособие для студентов всех форм, 757.37kb.
• New subject инфекционные болезни общие вопросы инфекционной патологии, 971.87kb.
• Курс читается в осеннем семестре и является общим для магистрантов всех специализаций., 62.84kb.
• Существует, по меньшей мере, несколько десятков определений этого понятия, в которых, 174.08kb.

Раздел «Экономико-математическое моделирование»

21. Модели зависимости спроса от дохода (кривые Энгеля). Эластичность спроса по доходу.
    

Кривые Энгеля, названные так в честь Э. Энгеля, показывают количество того или иного товара, которое потребитель готов купить при различных уровнях дохода (другие факторы, влияющие на спрос, принимаются как неизменные). Иными словами, данные кривые связывают количество приобретаемого товара с доходом покупателя. Для нормальных товаров характерен положительный наклон кривой Энгеля. С ростом доходов, население приобретает больше подобных товаров. Для товаров низшего качества наклон кривой Э. является отрицательным: м повышением доходов покупатели приобретают все меньшее количество низкокачественных продуктов. Если потребление товара не зависит от уровня дохода, то кривая Э. является вертикальной.



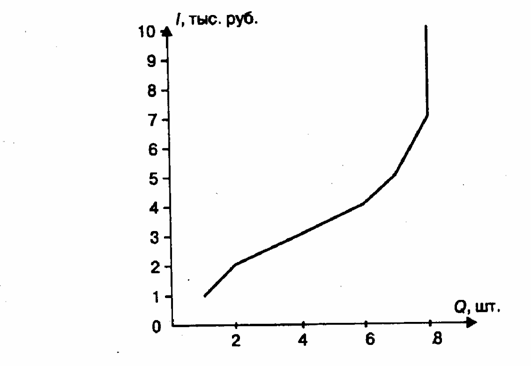
Кривые Э несут важную информацию о том, как реагирует спрос на изменение в денежных доходах покупателей. Закономерности в соотношении между доходами и объемами покупок, определенные энгелем, имеют важное значение для фирм-производителей при оценке ими возможных объемов продаж и рыночной конъюнктурой данного товара. В частности Э. были выведены след закономерности:

1.спрос на разные товары по разному реагирует на изменения в доходах покупателей, товары, воспринимаемые как предметы роскоши, являются более восприимчивыми к подобным изменениям.

2. потребление продуктов питания и других товаров первой необходимости слабо зависит от доходов населения, с ростом доходов уменьшается доля потребительского бюджета, расходуемая на закупку данных видов товаров.

3. с ростом доходов наблюдается более быстрое увеличение расходов потребителей на услуги (образовательные, медицинские.)


Для изучения изменения спроса в зависимости от доходов различных групп применяются модели степенного вида (функции Энгеля): D=AI^γ, A>0, γ>0 – параметры. Здесь γ имеет смысл коэффициента эластичности спроса по доходу; он, показывает, на сколько % увеличится (уменьшится) спрос на товар, если доход увеличится (уменьшится) на 1%.

Если коэффициент эластичности меньше единицы Ei(D)<1, то спрос на товар слабо зависит от дохода потребителей. Дополнительные расходы на эти товары убывают при возрастании дохода. В этом случае говорят, что спрос на этот товар неэластичен по доходу. Это относится в основном к предметам первой необходимости. Спрос называется нормально эластичным, если Ei(D) приблизительно равно 1, что имеет место для товаров длительного пользования. Для предметов «роскоши» обычно Ei(D)>1.Такой спрос называется суперэластичным, т.е. при увеличении дохода все большая часть его прироста тратится именно на товары этой группы.

Коэффициент приростной эластичности спроса по доходу: E_I(D)=(Ī*ΔD)/(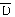*ΔI), где Ī – среднее значение дохода, 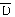- сред.значение спроса.

Результаты исследования изменения спроса по различным группам товаров обычно представляются в виде графиков, называемых кривыми Энгеля:


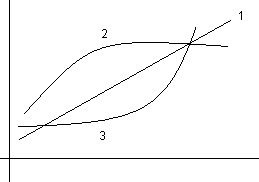1) γ=1, 2) γ<1, 3) γ>1


22. Модели производственных затрат и прибыли предприятия. Зона безубыточности. Точка максимума прибыли.


Простейшая экономико-математическая модель производства основана на том, что общие издержки С(х) на производство продукции в количестве х единиц состоят из:

1. Постоянных издержек (С₀)
   
2. Переменных (пропорциональных) С₁=b*x, где b – расходы (сырья, материалов, энергии) в расчете на 1 изделие в денежном выражении.
   

Модель совокупных издержек имеет вид:

С(х)= С₀+ b*x.

Параметры этой модели (C0 и b) определяются обычно одним из двух способов: 1) нормативным (отчетным) способом (нормативы задаются технологией производства и статьей производственных расходов или на основании отчетных данных); 2) из уравнения регрессии (при помощи статистич.данных).

Пример. 1) Нормативный способ: Дано, что постоянные затраты C0 составили 500 тыс.руб. в месяц, а переменные расходы «b» в расчете на одно изделие - 6 тыс.руб. Тогда линейная модель затрат имеет вид: C(x)=500+6x.

2) При помощи разработки линейного уравнения регрессии:

Пример. Имеется таблица наблюдений

Объем производства (x)	100	120	140	160	180	200
Производственные издержки C(x) млн.руб.	61	73	85	96	107	118

Применяя методы регрессионного анализа, получим уравнение:C(х)=4,71+0,57x

Линейная модель прибыли строится на основе данных о валовом доходе и производственных затратах: PR(x) = px - C(x), где px – валовой доход, PR – величина прибыли. Линейная модель прибыли имеет вид: PR(x)=px - C0 – bx = -C0 +(p-b)x .

Анализ этой формулы дает следующие результаты:

а) Если p£b (цена изделия не превышает удельных переменных затрат), то PR£0.

Производство не является прибыльным при любом количестве изделий.

б) Если p>b, то определяется точка безубыточности x₀, т.е. количество изделий, которому соответствует прибыль, равная нулю: x₀=C₀/(p-b).



Для всех x£x₀ производство убыточно PR£0; для всех x>x₀ производство прибыльно PR>0. При увеличении цены p точка безубыточности смещается влево. Безубыточность достигается при меньшем количестве изделий (см. линию Б₁).


Квадратичная модель затрат включает, кроме постоянных (С₀) и переменных (С₁) затрат, еще «сверхпропорциональные» затраты (С₂), в составе которых учитываются затраты на расширение производства, оплата сверхурочного труда и т.п. Для математического описания этого вида затрат используется степенная зависимость от объема выпуска С₂=kx², где k>0 – параметр модели.

Таким образом, квадратичная модель затрат имеет вид: С(х)=C₀+ C₁+ C₂= C₀+bx+kx².

График данной функции представляет собой монотонно возрастающую параболическую функцию при x ³ 0.




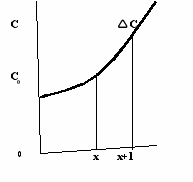
Для характеристики скорости возрастания издержек по мере роста выпуска продукции (х) используются понятия приростных и маргинальных издержек. Приростные издержки вычисляются по формуле êC=С(x+1)-C(x), которая характеризует затраты на выпуск дополнительной единицы продукции.

Маргинальными издержками называют приростные издержки в дифференциальной форме. Они вычисляются с использованием производной от функции затрат: МС=С’(x)=b+2kx

Пример.

Пусть C(x)=4,71+0,57x+0,001x², тогда маргинальные издержки равны

MC=C’ (x)=0,57+0,002x.

X	10	11	20	21
С(x)	10,51	11,10	16,51	17,12
êC	0,59		0,61
MC	0,59	0,592	0,61	0,612

Как видно из примера, приростные и маргинальные издержки возрастают по мере роста выпуска продукции.

Квадратичная модель прибыли строится на основе квадратичной модели затрат и имеет вид: PR(x)=px-(C₀+bx+kx²)=-C₀-kx²+(p-b)x. Анализ этой формулы дает следующие результаты:

а) Если p £ b, то PR £ 0, т.е. производство будет убыточным при любом количестве изделий.

б) Если p >b, то существуют две точки безубыточности, которым соответствует нулевая прибыль.



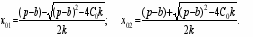
При анализе по объему производства возможны три случая:

а) если x₀₁, то PR < 0 и производство убыточно; б) если x₀₁ £ x £ x₀₂, то PR ³ 0 и производство прибыльно. Данный отрезок называется зоной безубыточности; в) если x>x₀₂, то PR < 0 и производство снова убыточно.

В центре зоны безубыточности находится точка максимума прибыли x_max, значение которой определяется из условия равенства нулю первой производной от функции PR(x)=-C₀-kx²+(p-b)x (1)

PR’(x)= -2kx+p-b=0 (2).

Отсюда X_max=(p-b)/2k (3).

В точке максимума прибыли [выражение (2)] p=MC(x), т.е. маргинальные издержки равны цене изделия. Величина максимальной прибыли равна (после подстановки 3 в 1).

PRmax=((p-b)2/4k)-C₀

График квадратичной функции прибыли имеет вид:





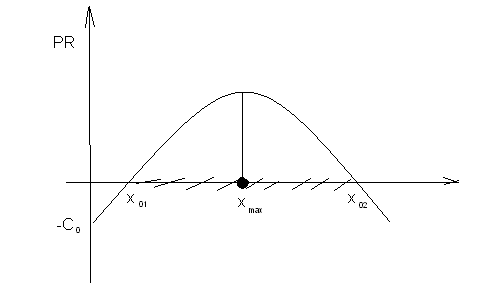
При увеличении цены изделия p, зона безубыточности расширяется, а точка максимума сдвигается направо.

Пример.

Пусть С(x)=4,71+0,57х+0,001х2, цена p=0,9. Тогда x₀₁=14,95»15; x₀₂=315; X_max=166.
Зона безубыточности (15 £ x £ 315). PR_max= 22,5 млн.руб.; МС(xmax)=0,9.

23. Экономико-математическая модель оптимизационной задачи (ОЗ) с линейной зависимостью между переменными.
    

Экономико-математические задачи, цель которых в нахождении оптимального (наилучшего) с точки зрения некоторого критерия (критериев) варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи решаются с помощью оптимальных моделей (ОМ) методами мат.программирования.

ОМ состоит из: целевой функции, области допустимых решений (в пределах которой осуществляется выбор решений) и системы ограничений, определяющих эту область.

Ограничения делятся на: линейные и нелинейные, детерминированные и стохастические (случайные).

Применяемые методы мат.программирования: линейное программирование, нелинейное, динамическое, целочисленное, выпуклое, исследование операций, геометрическое программирование.


Пусть b – количество ресурса вида i (i=1,2,3,….,n), aij – норма расхода i-го ресурса на единицу j-го вида продукции; хj – количество продукции вида j (j=1,2,3,…,n); Сj – прибыль (доход) от единицы этой продукции (в задачах на минимум – себестоимость продукции).

ОЗ линейного программирования (ЛП) в общем виде может быть сформулирована следующим образом:

Найти переменные хj (j=1,2,3,…,n), при которых целевая функция F(x)= Σcj*xj была бы max (min)-ной, не нарушая следующие ограничения:

_n

Σaij*xj≤bi, i=1,2,3,….,m₁,

^j=1

_n

Σaij*xj=bi, i=m₁+1, m₁+2,….m₂,

^j=1

_n

Σaij*xj≥bi, i=m₂+1, m₂+2,….m и условия неотрицательности искомых переменных: xj≥0.

^j=1

Все 3 случая можно привести к канонической форме, введя дополнительные переменные:

_n+k

Σaij*xj=bi, i=1,2,3,….,m₁, К – количество дополнительных переменных.

^j=1

Геометрическая интерпретация ОЗ линейного программирования.

До приобретения мебельного цеха Василий Тимофеев имел небольшую столярную мастерскую, где он мог трудился вместе со своим сыном по 9 часов в день, изготавливая тару двух видов – А и В, расходуя для этого ежедневно 4 куб. м древесины и 18 кг металла. Необходимо найти ежедневный оптимальный план производства двух видов тары(x₁ и x₂), при котором прибыль Василия была бы максимальной, а имеющиеся ресурсы использовались бы наилучшим образом. Условие задачи:





Оптимизационная модель задачи запишется следующим образом:

а) целевая функция: 4x₁+5x₂ стремится к max.

б) ограничения: 2x₁ + х₂ ≤12 (ограничение по металлу);

0,1x₁ + 0,5х₂ ≤4 (ограничение по древесине);

3,5x₁ + х₂≤18 (ограничение по труду).

в) условие неотрицательности переменных: x₁≥0;x₂≥0




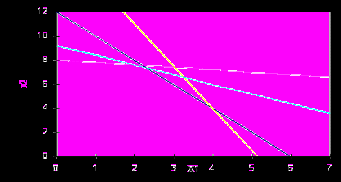
Х₁=2,2

Х₂= 7,5

Прибыль = 46,3 руб.

24. Модели мультипликатора в закрытой и открытой экономике.
    

Мультипликатор - числовой коэффициент, показывающий, во сколько раз сумма прироста/сокращения национального продукта, дохода или денежного обращения превышает инициирующую такое изменение сумму инвестиций, правительственных расходов, налоговых отчислений или вкладов в финансово-кредитные учреждения.


Закрытая экономика - национальная экономика закрытого типа (внешний мир опускается).

Мультипликатор (м/пл) госрасходов (простой м/пл Кейнса)

Под правительственными расходами понимаются расходы на содержание института гос-ва, а также гос-ные закупки товаров и услуг.

Простой м/пл Кейнса можно вывести из системы:

Y=C+I+G

C=a+b*Y, где I – инвестиционные расходы, С - потребительские расходы (кроме расходов на покупку жилья); а – автономное потребление, величина, не зависящая от размеров текущего располагаемого дохода; b – предельная склонность к потреблению (отношение прироста потребительских расходов к приросту располагаемого дохода); G – госзакупки товаров и услуг (кроме гос.трансфертов), Y – ВНП.




Y= a+b*Y+I+G Y-b*Y=a+I+G Y*(1-b)= a+I+G,

Y=(1/(1-b))*(a+I+G)=m*(a+I+G). При b=0,8, м/пл m=5.


Мультипликатор (м/пл) с учетом налогообложения в закрытой экономике

Y=C+I+G

C=a+b*(Y-Т)

Пусть T=t*Y, где t- предельная налоговая ставка. Тогда:

Y=a+b*(Y-T)+I+G, Y=a+b*(1-t)*Y+I+G, Y=(1/(1-b*(1-t)))*(a+I+G)=m*(a+I+G).




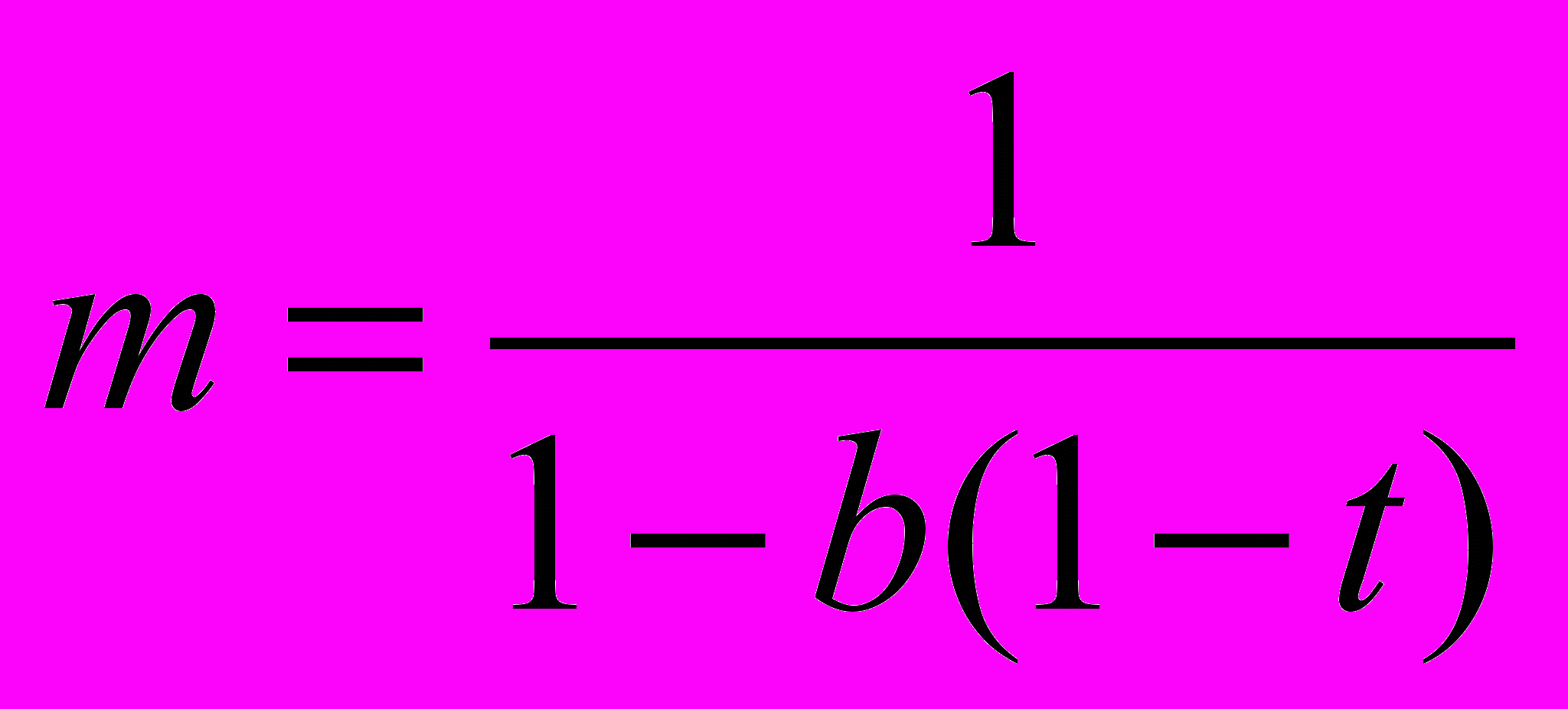
1)При b=0,8 и t=0,6 мультипликатор m = 1/(1-0,8(1-0,6))=1,47

2) При b=0,8 и t=0,2 мультипликатор m = 1/(1- 0,8(1-0,2))=2,78


Дополнение к формуле роста, предложенной Кейнсом I/(1 - с). Учитывает долю импорта, приходящуюся на каждую единицу потребляемой части национального дохода; вычисляется по формуле I/[1 - - (с + чистый импорт)].


Мультипликатор открытой экономики


Открытая экономика – это экономика, участвующая в международной торговле и международных финансовых отношениях с различными странами мира.

Мультипликатор открытой экономики

Согласно кейнсианской теории, общее уравнение открытой экономики

выглядит следующим образом:

Y = C + I + G + (экспорт - импорт), где Y - эффективный спрос, C -

потребление, I - инвестиции, G - государственные закупки.

Экспорт расширяет эффективный спрос, прибавляя к внутреннему

зарубежный сбыт товаров и услуг, между тем импорт замещает внутреннее

потребление альтернативной зарубежной продукцией, то есть возможности

внутреннего рынка уменьшаются. Характер возрастания национального дохода от

импорта/экспорта выражает мультипликатор открытой экономики, определяемый

по формуле: [pic].

Международные сопоставления показывают, например, что склонность к

импорту была в 60 - 80-е гг. высокой в Швейцарии и Великобритании, но

заметно более низкой - у США и Японии. Мультипликатор возрастания

национального дохода у этих стран обнаружил интересную зависимость:

Швейцария - 1.3;

Великобритания - 1.4;

США - 3.2;

Япония - 3.7.

Следует отметить, что импортная квота не является исчерпывающим

критерием при оценке перспектив роста национального дохода. Существует

обратная зависимость между экономическими масштабами страны и степенью

вовлеченности в мировое хозяйство.

Открытость экономики находится в зависимости и от государственного

регулирования. В связи с этим выделяют два основных вида государственной

политики: протекционизм и фритредерство. Протекционизм [лат. protectio

букв. прикрытие] представляет собой патронаж государства в сфере

внешнеэкономической деятельности, заключающийся в ограждении отечественного

производителя от внешней конкуренции. Фритредерство [англ. free trade

свободная торговля] выступает за свободу международной торговли и

невмешательство государства в хозяйственную жизнь.

Эффект м/пл в открытой экономике может быть найден в результате решения системы уравнений:

Y=C+I+G+Xn

C=a+b*(1-t)*Y

Xn=g-m´*Y, где m' – предельная склонность к импортированию: m'=ΔI_m/ΔY. Тогда:

Y=a+b*(1-t)*Y+I+G+ g-(m´*Y).







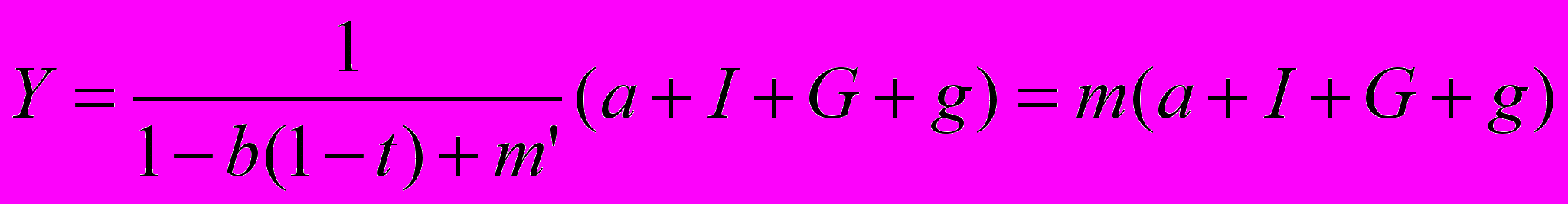
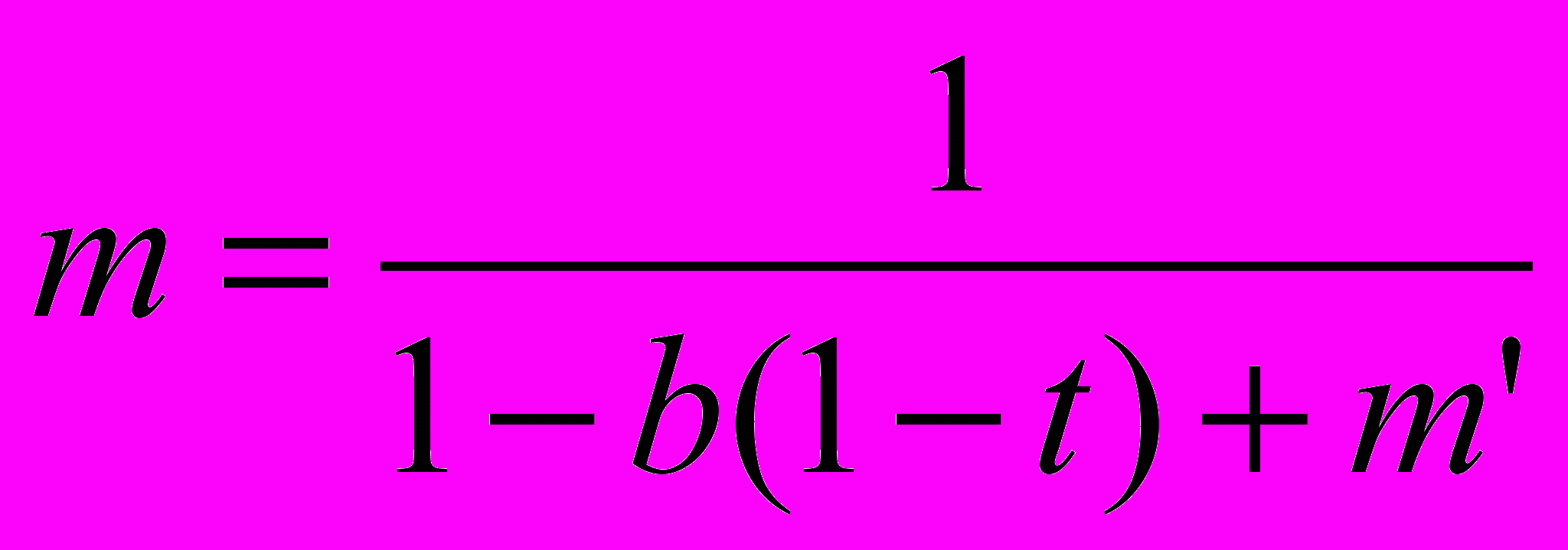
1)При b=0,8 и t=0,6 и m’= 0,3 мультипликатор m = 1/(1- 0,8(1-0,6)+0,3)=1,02

2) При b=0,8 и t=0,6 и m’= 0,1 мультипликатор m = 1/(1- 0,8(1-0,6)+0,1)=1,28

3) При b=0,8 и t=0,2 и m’= 0,1 мультипликатор m = 1/(1- 0,8(1-0,2)+0,1)=2,17

24. Экономико-математическая модель МОБ. Определение конечной и валовой продукции отраслей.
    

Технологическая матрица – совокупность коэф-тов (нормативов) прямых затрат на производство единицы продукции.

В основе схемы МОБ положено представление о нац.экномике как о совокупности n чистых (технологических или условных) отраслей. Предполагается, что 1 отрасль производит только 1 продукт, и что 1 продукт производится только 1 отраслью. Каждая отрасль отражается в балансе как производящая, так и потребляющая. Совокупный продукт делится на: промежуточный и конечный.

Схема МОБ:

Производящие отрасли	Потребляющие отрасли					Конечный продукт	Валовый продукт
	1	2	3	…	N
1	X11	X12	X13	…	X1n	Y1	X1
2	X21	X22	X23	…	X2n	Y2	X2
3	X31	X32	X33	…	X3n	Y3	X3
…	…	…	…	…	…	…	…
n	Xn1	Xn2	Xn3	…	xnn	yn	Xn
Амортизация	С1	С2	С3	…	Сn
Оплата труда	V1	V2	V3	…	vn
Чистый доход	M1	M2	M3	…	mn
Валовый продукт	X1	X2	X3	…	xn

Первый квадрант МОБ отражает материальную связь, промежуточное потребление продукции. Xij –стоимость средств производства, произведенных отраслью i и потребленных отраслью j.

Второй квадрант отражает конечную продукцию всех отраслей материального производства. Конечная продукция идет на:

- потребление домашних хозяйств

-общественное потребление (госрасходы)

- Инвестиции

- экспорт (за минусом импорта).

3-й квадрант характеризует условно чистую продукцию всех отраслей производства по доходам. Под условно чистой продукцией (zj) понимается сумма амортизации, оплаты труда и чистого дохода.

4-й квадрант отражает конечное перераспределение и использование национального дохода.

Для МОБ можно записать ряд соотношений:

• По столбцам: xj=Σxij + zj, j=1,2,…n.
  
• По строкам: xi= Σxij + yi; Σxj=Σxi Σzj = Σyi