Geum.ru

Учебно-методический комплекс дисциплины «статистика» Направление 080100 «экономика»

Вид материалаУчебно-методический комплекс

Содержание


Раздел 5. корреляционно-регрессионный анализ
Раздел 6. временные ряды (ряды динамики)
Для менеджера предпочтительно
Раздел 7. индексы
Индексы — относительные показатели, предназначенные для описания изменения какой-либо величины во времени или в пространстве.
Подобный материал:
1   2   3   4   5   6   7

РАЗДЕЛ 5. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ


Для менеджера большинство решений, принятие которых строятся на основе рассмотрения хозяйственных ситуаций, весьма важно уметь анализировать причинно-следственные связи в организационных системах. Эффективным инструментом их описания является корреляционно-регрессионный анализ, методы многомерной классификации.

В данной главе мы будем рассматривать факторные корреляционные связи, которые характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные. При корреляционной связи изменения результативного признака обусловлено влиянием факторного признака не всецело, а лишь частично, так как возможно влияние прочих факторов, различных по составу, направлению и силе действия на отдельные единицы статистической совокупности.

«Если две какие-либо характеристики, полученные для одного и того же объекта имеют тенденцию изменяться совместно, так, что создается возможность предсказать величину одной из них по значению другой, то говорят, что эти характеристики коррелируют между собой».

Основная задача корреляционного анализа — ответить на вопрос — существует ли между признаками корреляционная зависимость.

Корреляционная зависимость - зависимость случайных величин (признаков), при которой изменению среднего значения одной соответствует изменение среднего значения другой случайной величины.

Показатели тесноты связи между признаками называют коэффициентами корреляции.


Задание №1

По данным таблицы 5.2 провести корреляционно – регрессионный анализ связи между дозой удобрения (х) и урожайностью зерновых культур (y):

1.Определить факторный и результативный признаки.

2.Начертить графики зависимости результативного признака от факторного, определить по нему тип уравнения регрессии, направление и силу связи.

3.Рассчитать параметры уравнения регрессии, решить уравнение регрессии и результаты отразить на графике.

4.Расчитать показатели тесноты связи и охарактеризовать силу связи.

Расчетная таблица 5.1 для определения выше перечисленных показателей.

Таблица 5.1

Исходные данные
Решение уравнения регрессии
Расчет показателей тесноты связи

№
x
y


xy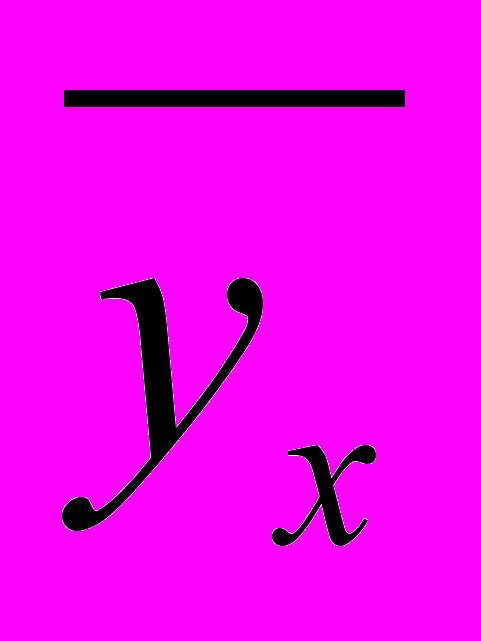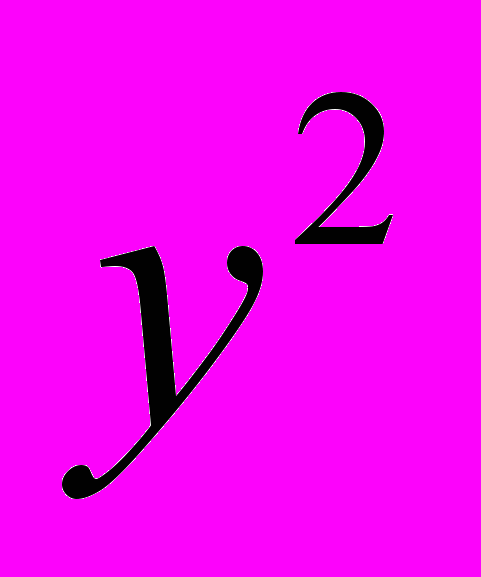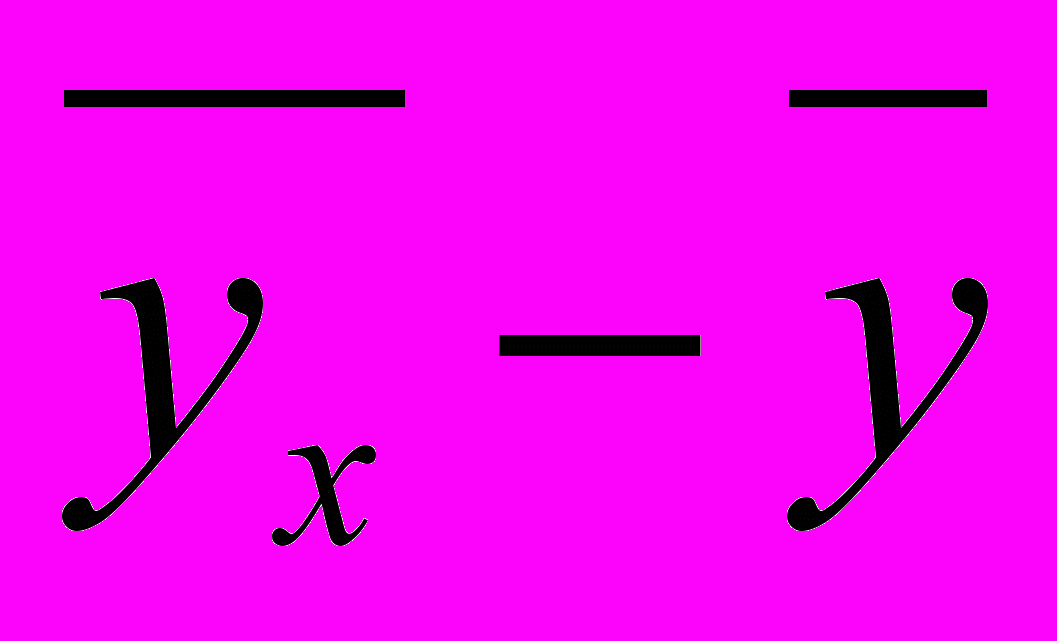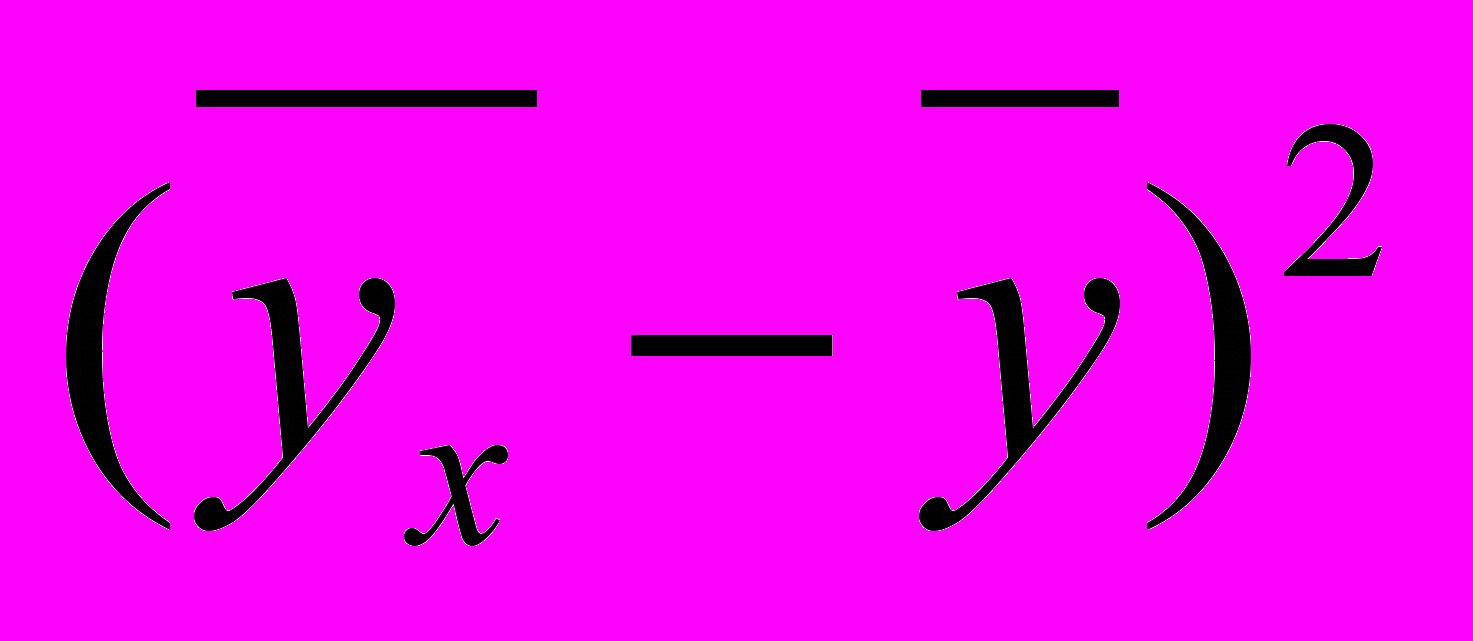








1

2

3

4

5

6

7

8

9

10
























итого


















-





Таблица 5.2

Данные по урожайности зерновых культур и дозам удобрения

№ хоз.
№ варианта

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

1
3,8
19,5
3,9
19,6
4,0
19,7
4,1
19,8
4,2
19,9
4,3
20,0
4,4
20,1
4,5
20,2
4,6
20,3
4,7
20,4
4,8
20,5
4,9
20,6
5,0
20,7
5,1
20,8
5,2
20,9

2
2,0
15,8
2,1
15,9
2,2
16,0
2,3
16,1
2,4
16,2
2,5
16,3
2,6
16,4
2,7
16,5
2,8
16,6
2,9
16,7
3,0
16,8
3,1
16,9
3,2
17,0
3,3
17,1
3,4
17,2

3
2,3
16,9
2,4
17,0
2,5
17,1
2,6
17,2
2,7
17,3
2,8
17,4
2,9
17,5
3,0
17,6
3,1
17,7
3,2
17,8
3,3
17,9
3,4
18,0
3,5
18,1
3,6
18,2
3,7
18,3

4
2,1
17,4
2,2
17,5
2,3
17,6
2,4
17,7
2,5
17,8
2,6
17,9
2,7
18,0
2,8
18,1
2,9
18,2
3,0
18,3
3,1
18,4
3,2
18,5
3,3
18,6
3.4
18,7
3,5
18,8

Продолжение таблицы 5.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

5
2,2
17,0
2,3
17,1
2,4
17,2
2,5
17,3
2,6
17,4
2,7
17,5
2,8
17,6
2,9
17,7
3,0
17,8
3,1
17,9
3,2
18,0
3,3
18,1
3.4
18,2
3,5
18,3
3,6
18,4

6
3,9
16,4
4,0
16,5
4,1
16,6
4,2
16,7
4,3
16,8
4,4
16,9
4.5
17,0
4,6
17,1
4,7
17,2
4,8
17,3
4,9
17,4
5,0
17,5
5,1
17,6
5,2
17,7
5,3
17,8

7
0,7
15,0
0,8
15,1
0,9
15,2
1,0
15,3
1,1
15,4
1,2
15,5
1,3
15,6
1,4
15,7
1,5
15,8
1,6
15,9
1,7
16,0
1,8
16,1
1,9
16,2
2,0
16,3
2,1
16,4

8
0,6
15,6
0,7
15,7
0,8
15,8
0,9
15,9
1,0
16,0
1,1
16,1
1,2
16,2
1,3
16,3
1,4
16,4
1,5
16,5
1,6
16,6
1,7
16,7
1,8
16,8
1,9
16,9
2,0
17,0

9
2,0
16,5
2,1
16,5
2,2
16,6
2,3
16,7
2,4
16,8
2,5
16,9
2,6
17,0
2,7
17,1
2,8
17,2
2,9
17,3
3,0
17,4
3,1
17,5
3,2
17,6
3,3
17,7
3,4
17,8

10
2,0
13,1
2,1
13,2
2,2
13,3
2,3
13,4
2,4
13,5
2,5
13,6
2,6
13,7
2,7
13,8
2,8
13,9
2,9
14,0
3,0
14,1
3,1
14,2
3,2
14,3
3,3
14,4
3,4
14,5

Продолжение таблицы 5.2

№ хоз.
№ варианта

16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

1
5,3
30,0
5,4
30,1
5,5
30,2
5,6
30,3
5,7
30,4
5,8
30,5
5,9
30,6
6,0
30,7
6,1
30,8
6,2
30,9
6,3
40,1
6,4
40,2
6,5
40,3
6,6
40,4
6,7
40,5

2
3,4
17,3
3,5
17,4
3,6
17,5
3,7
17,6
3,8
17,8
3,9
17,9
4,0
18,0
4,1
18,1
4,2
18,2
4,3
18,3
4,4
18,4
4,5
18,5
4,6
18,6
4,7
18,7
4,8
18,8

3
3,7
18,3
3,8
18,4
3,9
18,5
4,0
18,6
4,1
18,7
4,2
18,8
4,3
18,9
4,4
19,0
4,5
19,1
4,6
19,2
4,7
19,3
4,8
19,4
4,9
19,5
5,0
19,6
5,1
19,7

4
3,5
18,8
3,6
18,9
3,7
19,0
3,8
19,1
3,9
19,2
4,0
19,3
4,1
19,4
4,2
19,5
4,3
19,6
4,4
19,7
4,5
19,8
4,6
19,9
4,7
20,0
4,8
20,1
4,9
20,2

Продолжение таблицы 5.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

5
3,6
18,4
3,7
18,5
3,8
18,6
3,9
18,7
4,0
18,8
4,1
18,9
4,2
19,0
4,3
19,1
4,4
19,2
4,5
19,3
4,6
19,4
4,7
19,5
4,8
19,6
4,9
19,7
5,0
19,8

6
5,3
17,9
5,4
18,0
5,5
18,1
5,6
18,2
5,7
18,3
5,8
18,4
5,9
18,5
6,0
18,6
6,1
18,7
6,2
18,8
6,3
18,9
6,4
19,0
6,5
19,1
6,6
19,2
6,7
19,3

7
2,1
16,5
2,2
16,6
2,3
16,7
2,4
16,8
2,5
16,9
2,6
17,0
2,7
17,1
2,8
17,2
2,9
17,3
3,0
17,4
3,1
17,5
3,2
17,6
3,3
17,8
3,4
17,9
3,5
18,0

8
2,0
17,1
2,1
17,2
2,2
17,3
2,3
17,4
2,4
17,5
2,5
17,6
2,6
17,7
2,7
17,8
2,8
17,9
2,9
18,0
3,0
18,1
3,1
18,2
3,2
18,3
3,3
18,4
3,4
18,5

9
3,4
17,9
3,5
18,0
3,6
18,1
3,7
18,2
3,8
18,3
3,9
18,4
4,0
18,5
4,1
18,6
4,2
18,7
4,3
18,8
4,4
18,9
4,5
19,0
4,6
19,1
4,7
19,2
4,8
19,3

10
3,4
14,6
3,5
14,7
3,6
14,8
3,7
14,9
3,8
15,0
3,9
15,1
4,0
15,2
4,1
15,3
4,2
15,4
4,3
15,5
4,4
15,6
4,5
15,7
4,6
15,8
4,7
15,9
4,8
16,0

РАЗДЕЛ 6. ВРЕМЕННЫЕ РЯДЫ (РЯДЫ ДИНАМИКИ)

Процесс развития, изменения во времени социально-экономических явлений в статистике называют динамикой. В данном разделе мы рассмотрим статистические методы, позволяющие анализировать динамические, изменяющиеся во времени, характеристики социально-экономических явлений.

Ряды динамики получают в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.

В зависимости от качественной особенности изучаемого явления, а также вида исходных данных ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

При изучении ряда динамики возникает необходимость получения обобщающей величины его абсолютных уровней. Для этого определяют средний уровень ряда как среднюю величину из совокупности абсолютных уровней ряда за те или иные периоды времени.

Такая величина называется средней хронологической. Методы ее расчета зависят от вида ряда динамики и способов получения статистических данных.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней ряда между собой (цепные показатели) или с уровнем, выбранным за базис (базисные показатели): абсолютные приросты, темпы роста, темпы прироста.

Сводной, обобщающей характеристикой интенсивности изменения уровней ряда динамики является средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень ряда.

Важной управленческой задачей, решаемой с использованием рядов динамики является определение общей тенденции развития. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным.

При изучении в рядах динамики обшей тенденции развития применяются различные приемы и методы.

Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями.

Для менеджера предпочтительно применение именно этого метода, поскольку он определяет закон, по которому можно достаточно точно спрогнозировать значения уровней ряда. Однако, применение его требует достаточных знаний в области высшей математики и математической статистики.

Задание №1

По данным таблицы 6.1 проанализировать динамику урожайности зерновых культур, для этого::

1.Изобразить ряд динамики урожайности графически в виде линейной диаграммы.

2.Вычислить аналитические показатели ряда динамики цепные и базисные: абсолютный прирост, темп роста и прироста, абсолютное значение 1 % прироста. Расчеты оформить в таблицу 6.2.

3.Рассчитать средний абсолютный прирост и средние темпы роста и прироста. Сделать выводы.

4.Провести аналитическое выравнивание ряда динамики по прямой и по параболе. Расчеты оформить в таблицу 6.3. Выровненные данные нанести на график.

5.Оценить с помощью коэффициента Аппроксимации какое уравнение (прямой или параболы) лучше воспроизводит фактические уровни ряда динамики. Расчеты оформить в таблицу 6.4.


Таблица 6.1

Динамика урожайности зерновых культур

год
Урожайность зерновых культур, ц/га, (по вариантам)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

1
20,0
20,1
20,2
20,3
20,4
20,5
20,6
20,7
20,8
20,9
21,0
21,1
21,2
21,3
21,4
21,5
21,6
21,7
21,8
21,9
22,0
22,1
22,2
22,3
22,4
22,5
22,6
22,7
22,8
22,9

2
22,5
22,6
22,7
22,8
22,9
23,0
23,1
23,2
23,3
23,4
23,5
23,6
23,7
23,8
23,9
24,0
24,1
24,2
24,3
24,4
24,5
24,6
24,7
24,8
24,9
25,0
25,1
25,2
25,3
25,4

3
18,1
18,2
18,3
18,4
18,5
18,6
18,7
18,8
18,9
19,0
19,1
19,2
19,3
19,4
19,5
19,6
19,7
19,8
19,9
20,0
20,1
20,2
20,3
20,4
20,5
20,6
20,7
20,8
20,9
21,0

4
20,9
21,0
21,1
21,2
21,3
21,4
21,5
21,6
21,7
21,8
21,9
22,0
22,1
22,2
22,3
22,4
22,5
22,6
22,7
22,8
22,9
23,0
23,1
23,2
23,3
23,4
23,5
23,6
23,7
23,8

5
26,0
26,1
26,2
26,3
26,4
26,5
26,6
26,7
26,8
26,9
27,0
27,1
27,2
27,3
27,4
27,5
27,6
27,7
27,8
27,9
28,0
28,1
28,2
28,3
28,4
28,5
28,6
28,7
28,8
28,9

Продолжение таблицы 6.1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

6
22,5
22,6
22,7
22,8
22,9
23,0
23,1
23,2
23,3
23,4
23,5
23,6
23,7
23,8
23,9
24,0
24,1
24,2
24,3
24,4
24,5
24,6
24,7
24,8
24,9
25,0
25,1
25,2
25,3
25,4

7
31,1
31,2
31,3
31,4
31,5
31,6
31,7
31,8
31,9
32,0
32,1
32,2
32,3
32,4
32,5
32,6
32,7
32,8
32,9
33,0
33,1
33,2
33,3
33,4
33,5
33,6
33,7
33,8
33,9
34,0

8
32,1
32,2
32,3
32,4
32,5
32,6
32,7
32,8
32,9
33,0
33,1
33,2
33,3
33,4
33,5
33,6
33,7
33,8
33,9
34,0
34,1
34,2
34,3
34,4
34,5
34,6
34,7
34,8
34,9
35,0

9
30,3
30,4
20,5
30,6
30,7
30,8
30,9
31,0
31,1
31,2
31,3
31,4
31,5
31,6
31,7
31,8
31,9
32,0
32,1
32,2
32,3
32,4
32,5
32,6
32,7
32,8
32,9
33,0
33,1
33,2

10
31,0
31,1
31,2
31,3
31,4
31,5
31,6
31,7
31,8
31,9
32,0
32,1
32,2
32,3
32,4
32,5
32,6
32,7
32,8
32,9
33,0
33,1
33,2
33,3
33,4
33,5
33,6
33,7
33,8
33,9



Таблица 6.2

Расчетная таблица для вычисления аналитических показателей ряда динамики

Годы №

п/п
Урожайность зерновых культур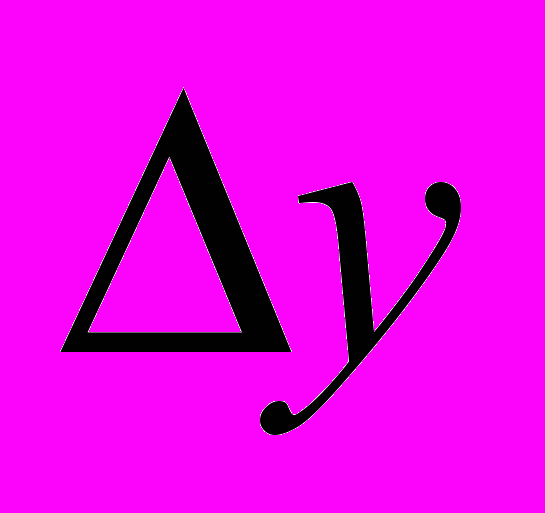, ц/га
, ц/га
Тр, %
Тпр, %
, ц/га

цепной
базисный
цепной
базисный
цепной
базисный

1
























2
























3
























4
























5
























6
























7
























8
























9
























10
























Таблица 6.3

Расчетная таблица для вычисления параметров уравнений прямой и параболы

Годы №

п/п
Урожайность

зерновых культур, ц/га
прямая
парабола

t
y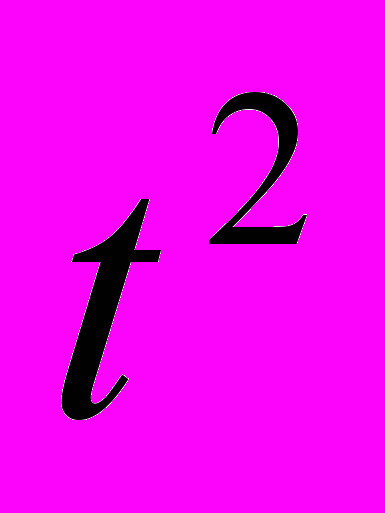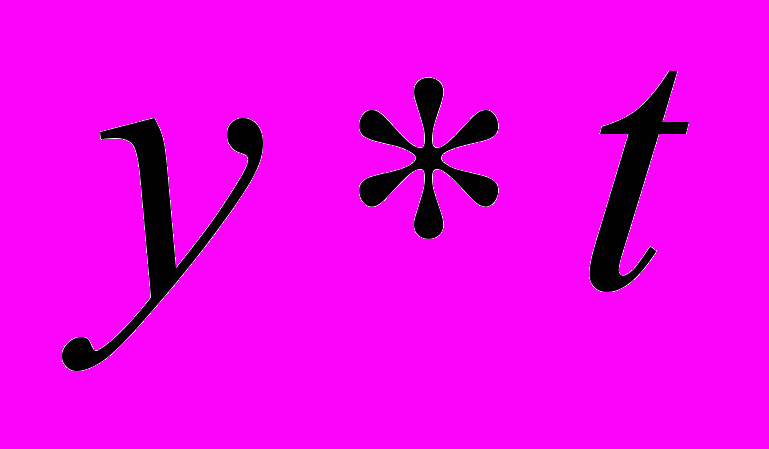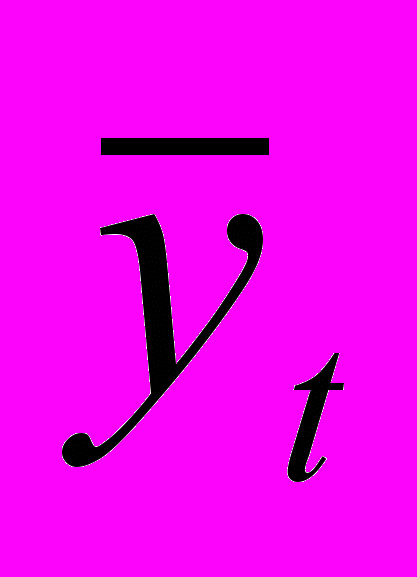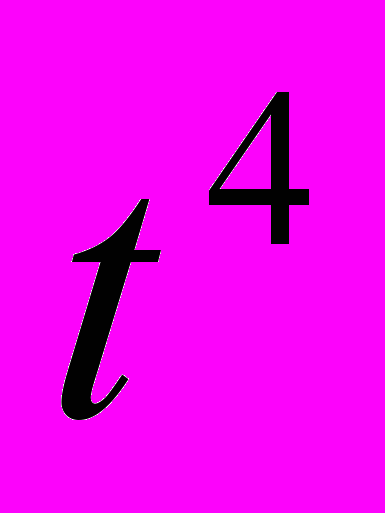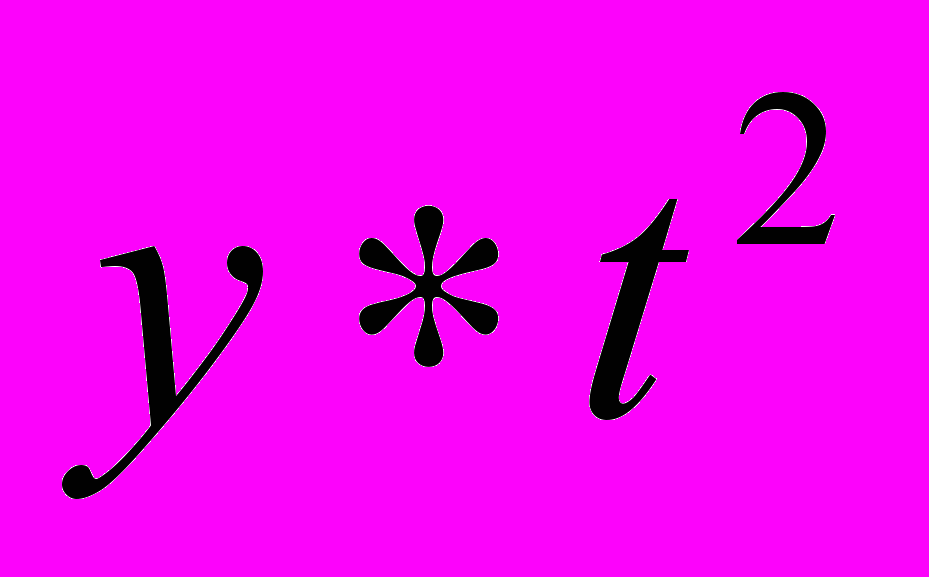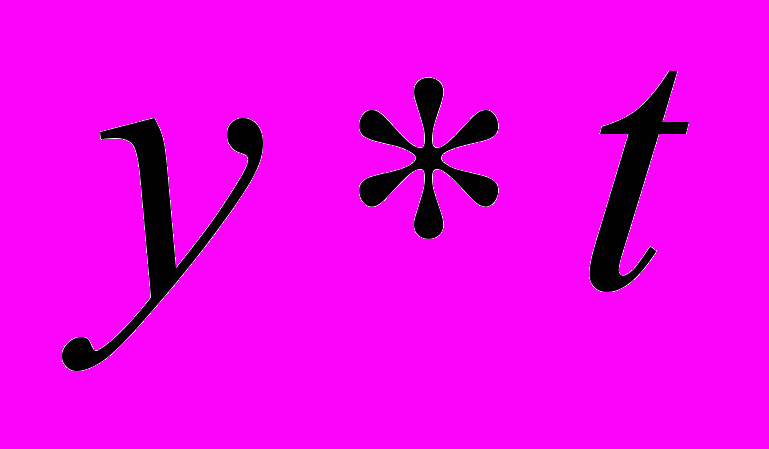












1



























2



























3



























4



























5



























6



























7



























8



























9



























10



























итого



-









-






-

Таблица 6.4

Расчетная таблица параметров коэффициента аппроксимации

Годы №

п/п
Урожай

ность

зерновых

культур, ц/га
прямая
парабола













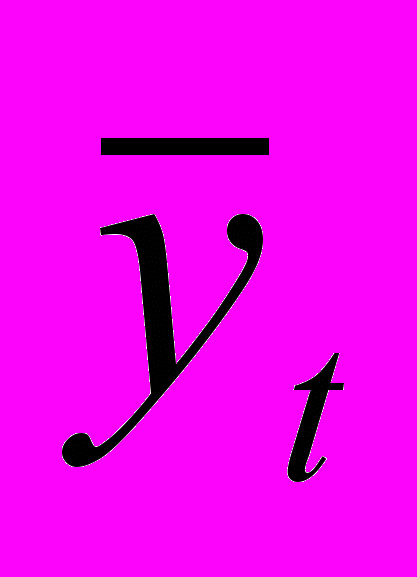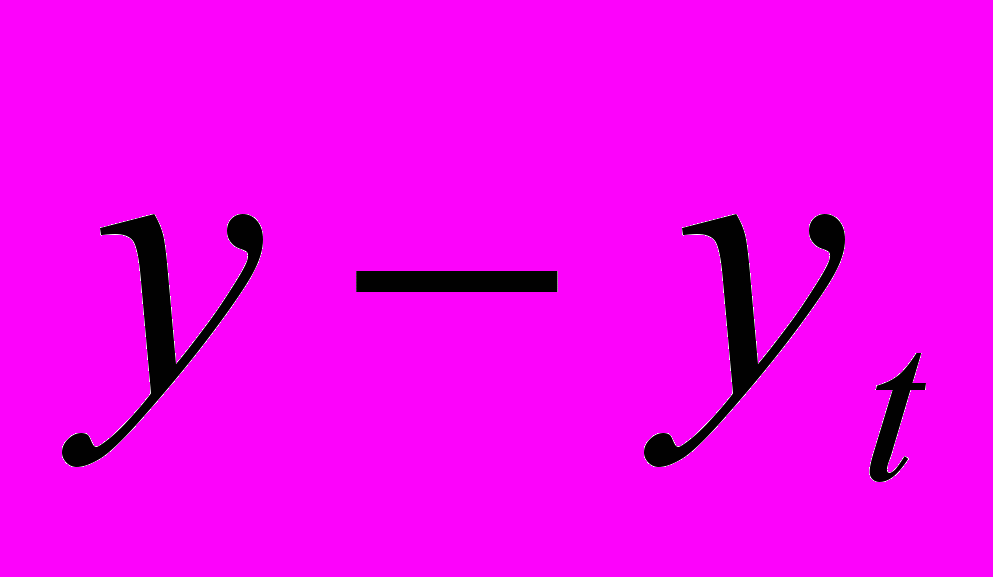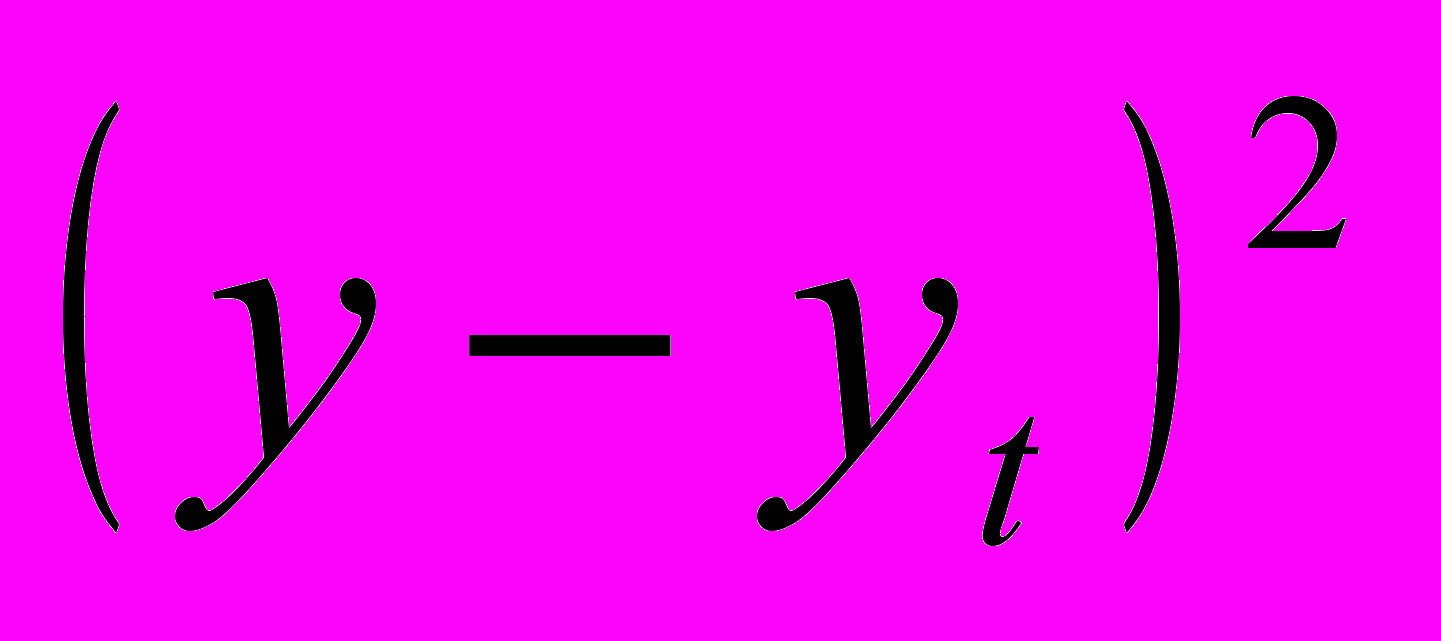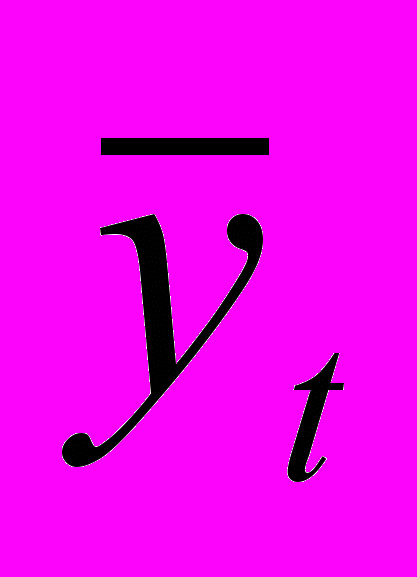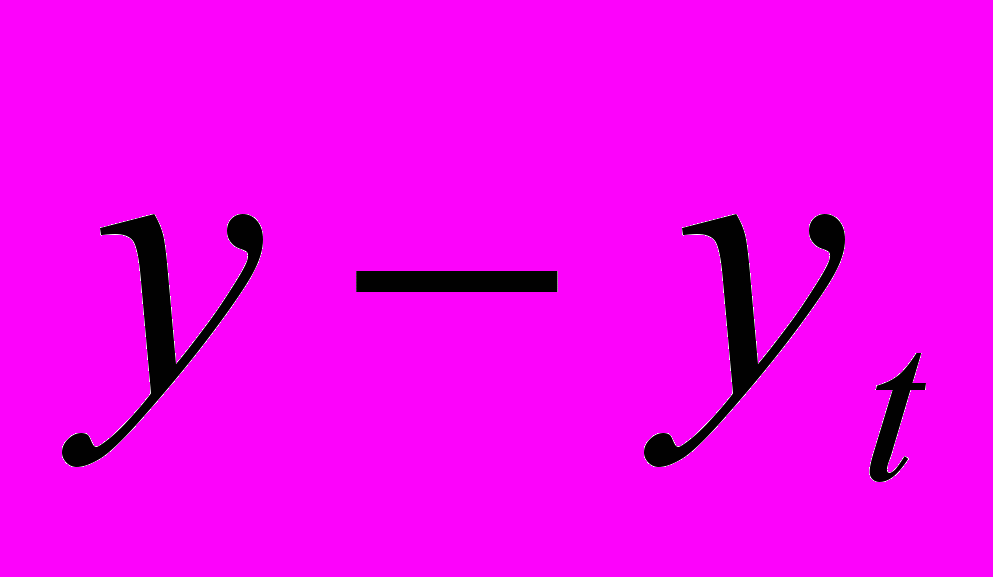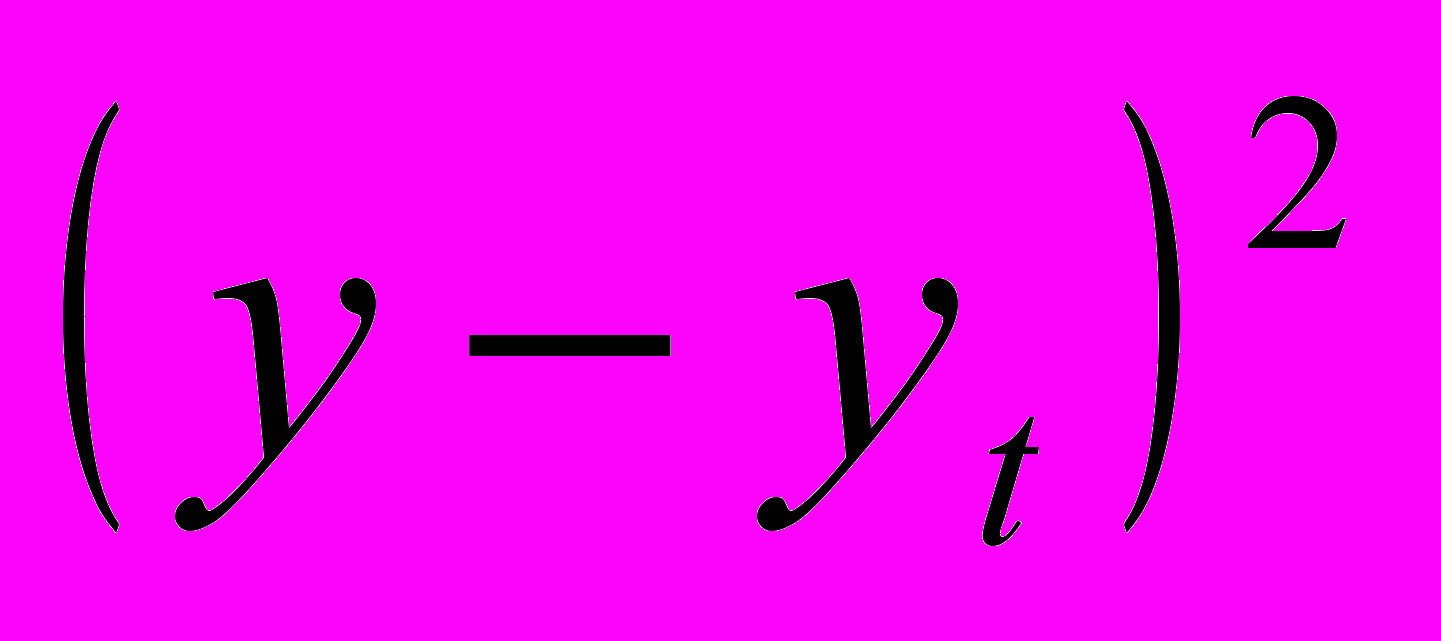1





















2





















3





















4





















5





















6





















7





















8





















9





















10





















итого
-
-
-



-
-



РАЗДЕЛ 7. ИНДЕКСЫ


Статистическая наука имеет в своем арсенале метод, позволяющий соизмерить показатели какого-либо явления во времени и пространстве и позволять сравнивать фактические данные с любым эталоном, в качестве которого может быть план, прогноз или какой-либо норматив. Это индексный метод, оперирующий с относительными показателями, в статистике называемым «индексами».

Изучив этот раздел, вы:
  • поймете, что такое индексный метод;
  • научитесь применять индексный метод для анализа;
  • на примерах изучите способы расчета индексов: индексов цен, физического объема;
  • сможете самостоятельно рассчитывать индексы инфляции и приводить к «неизменным ценам» свои доходы, курсы валют, стоимости основных фондов и т.п.

Индексы — относительные показатели, предназначенные для описания изменения какой-либо величины во времени или в пространстве.

Индекс — сводный, обобщенный итоговый показатель изменения изучаемого явления.


Задание №1

Таблица 7.1

Объем продаж и цены плодово-ягодной продукции

Наименование товара
Июль
Август
Расчетные графы

Цена за 1 кг, руб.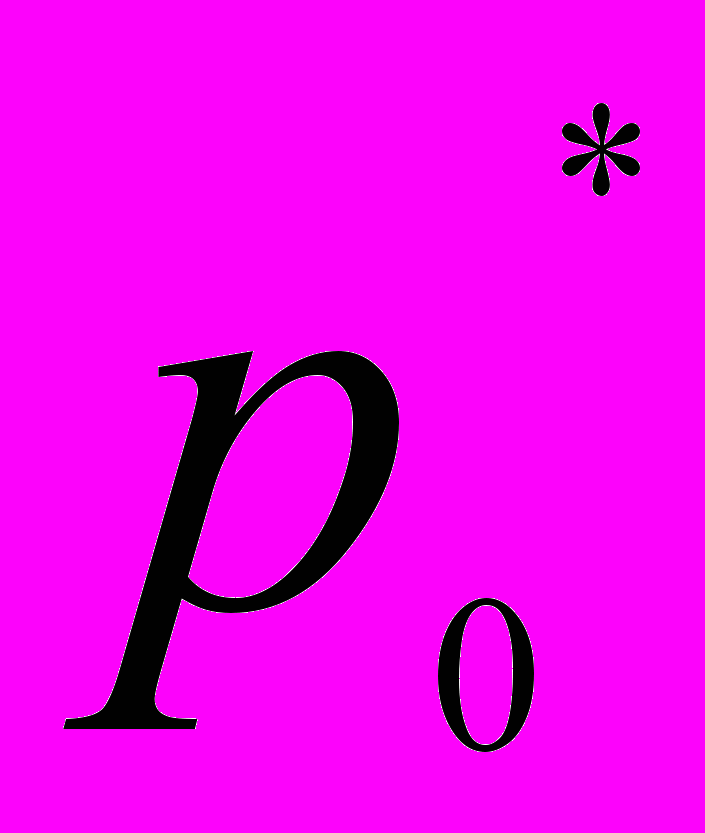
Продано, т.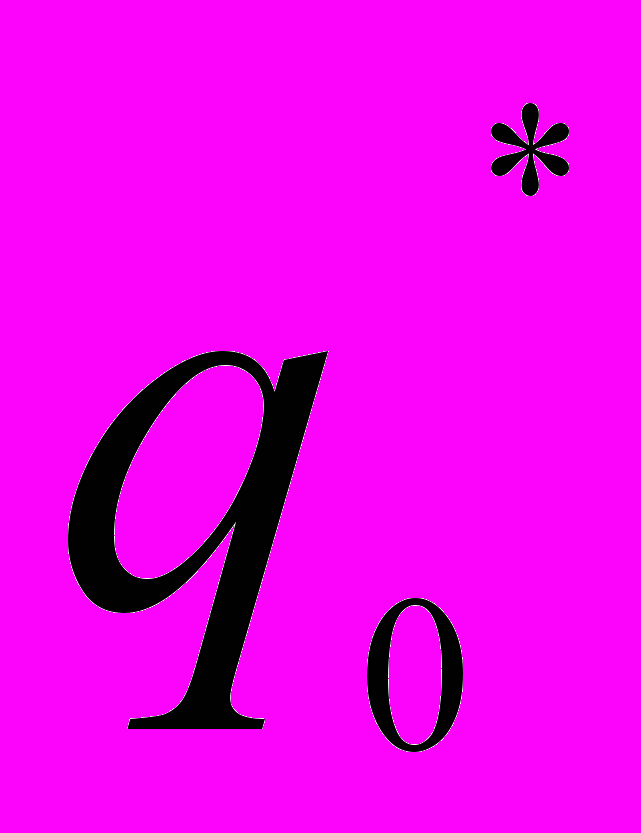

Цена за 1 кг, руб.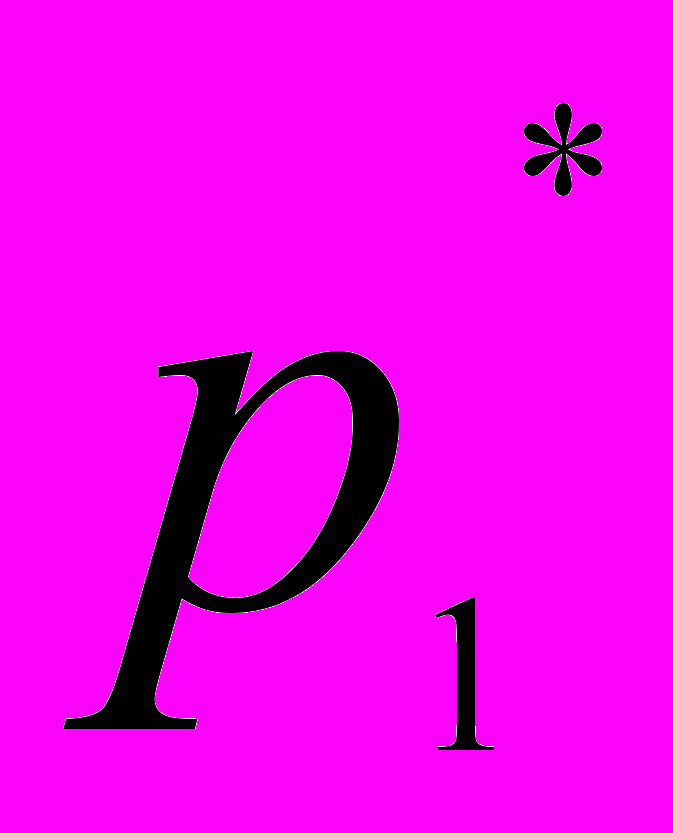
Продано, т.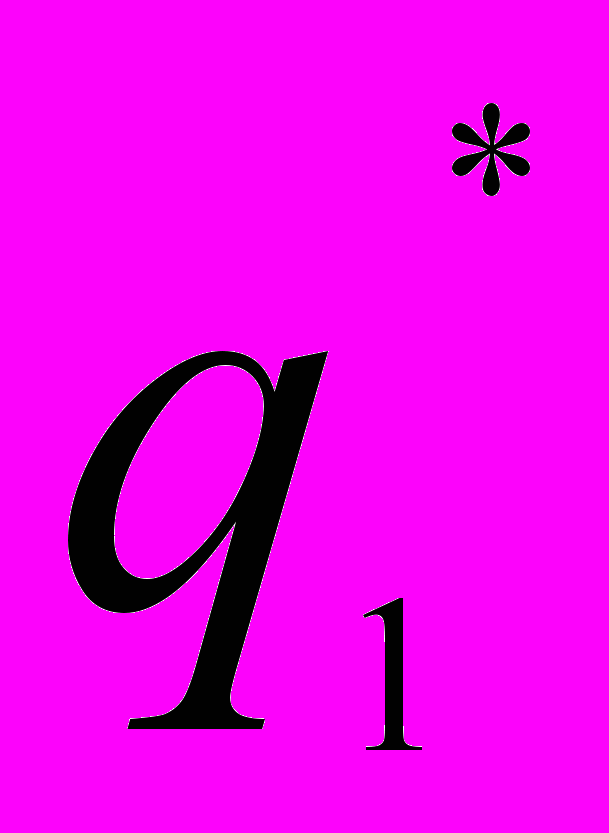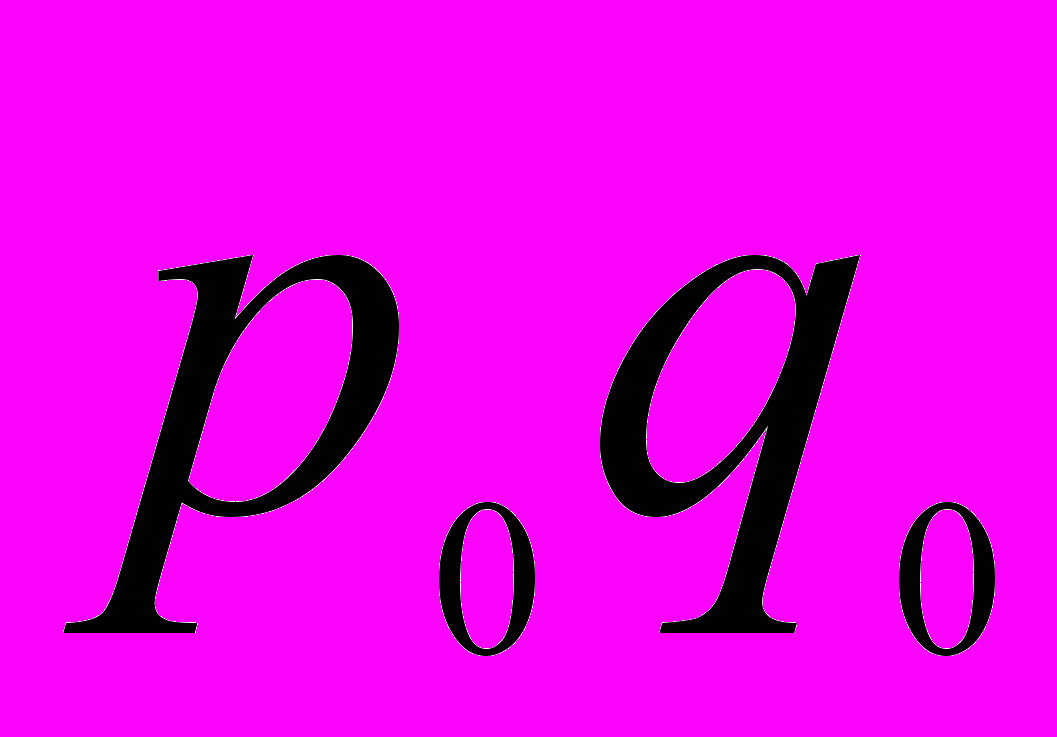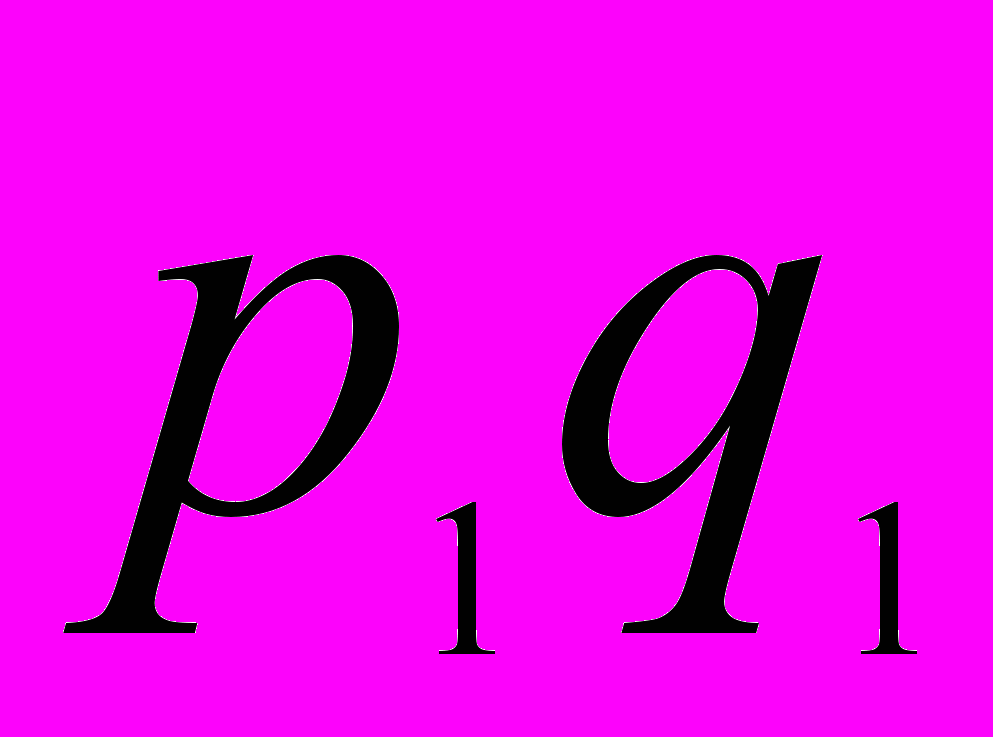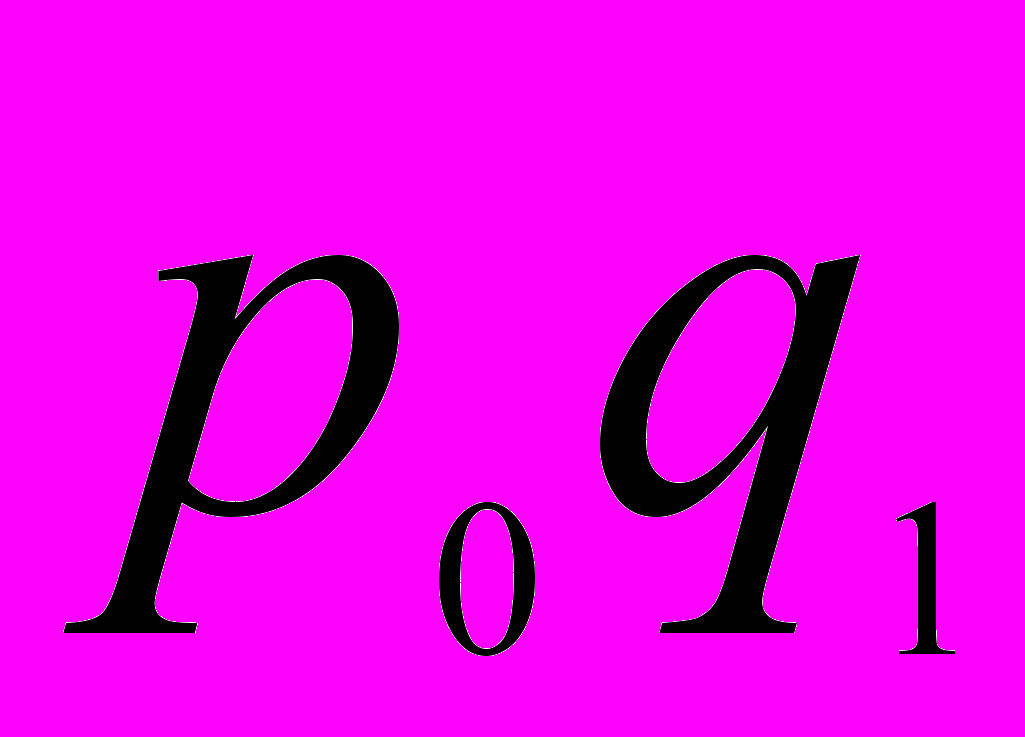






Черешня

Персики

Виноград
120

110

90
18

22

20
120

100

70
15

27

24









Итого
--
--
--
--










По данным таблицы 7.1 рассчитать сводный индекс товарооборота, сводный индекс цен, сводный индекс физического объема Ласпейреса. Используя взаимосвязь индексов физического объема и цен, проверить правильность расчета индекса товарооборота.


Задание №2

Таблица 7.2

Производительности труда на предприятии

Вид продукции
Затраты времени на 1 изделие, чел.-ч.
Произведено, шт.
Расчетные графы, чел.-ч.

Январь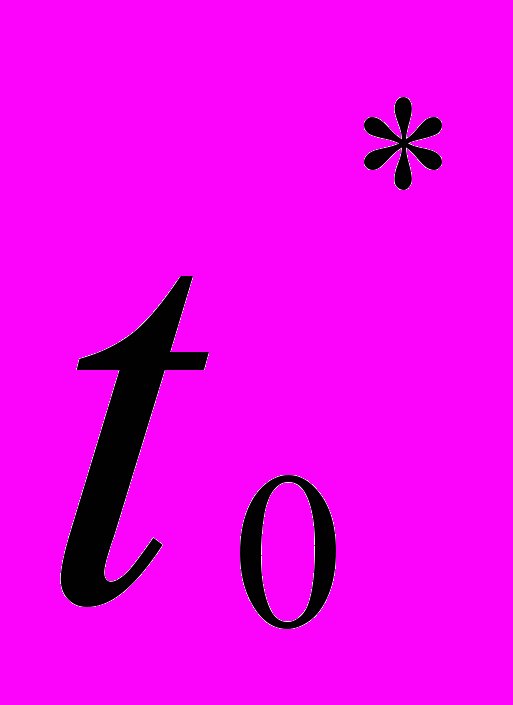
Февраль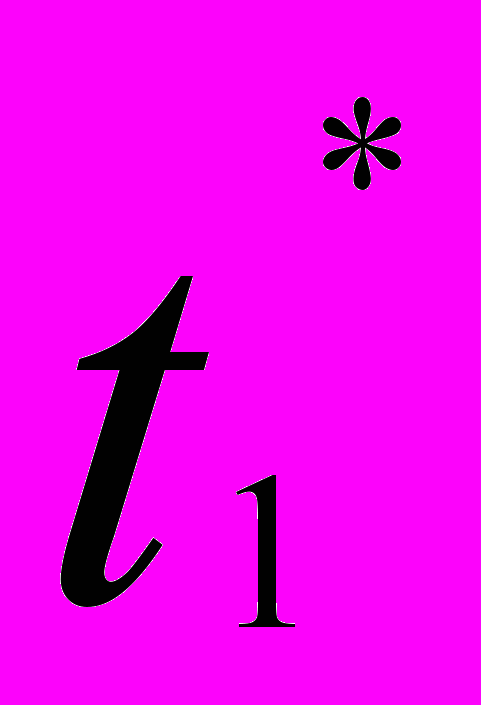
Январь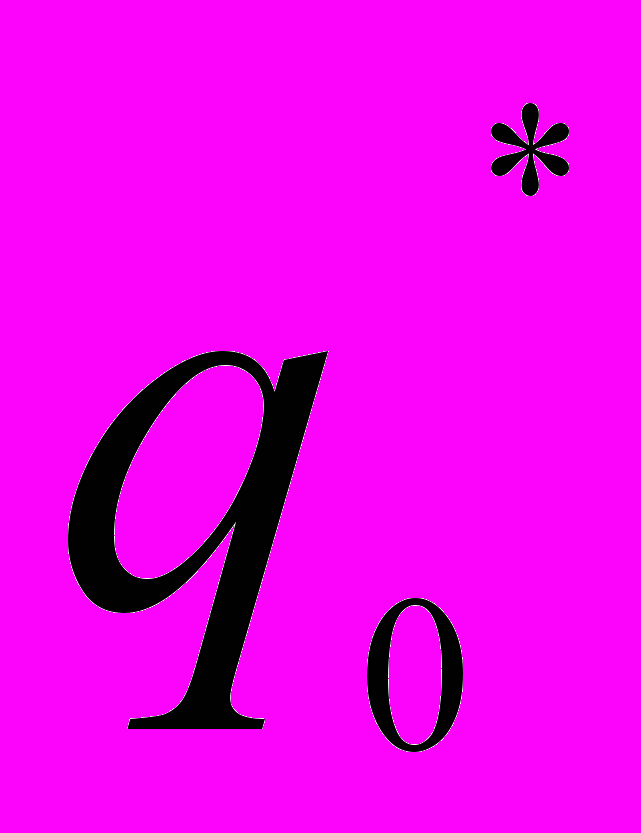

Февраль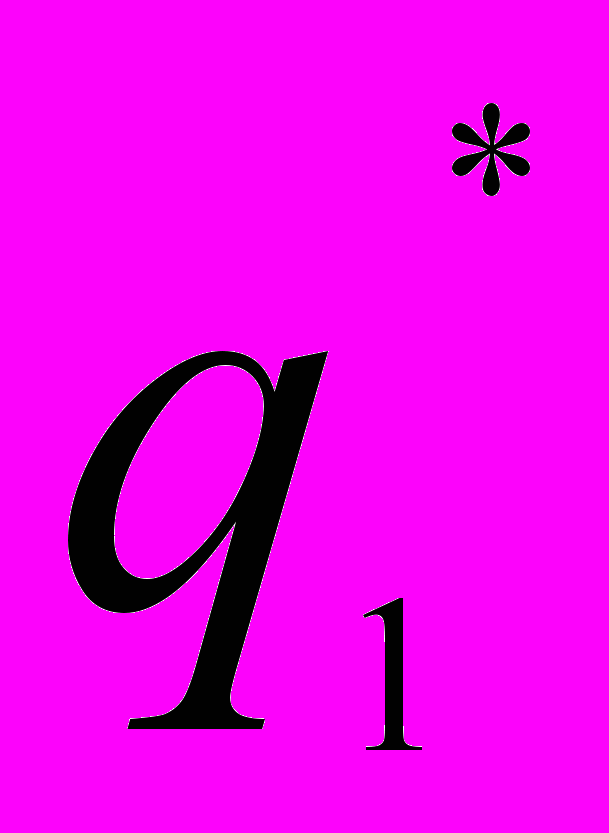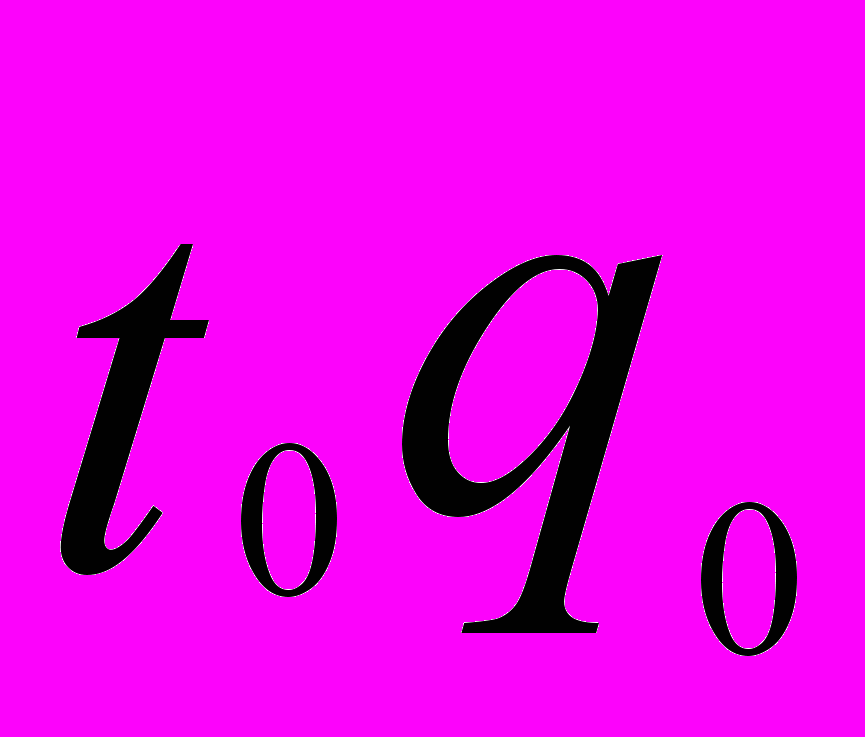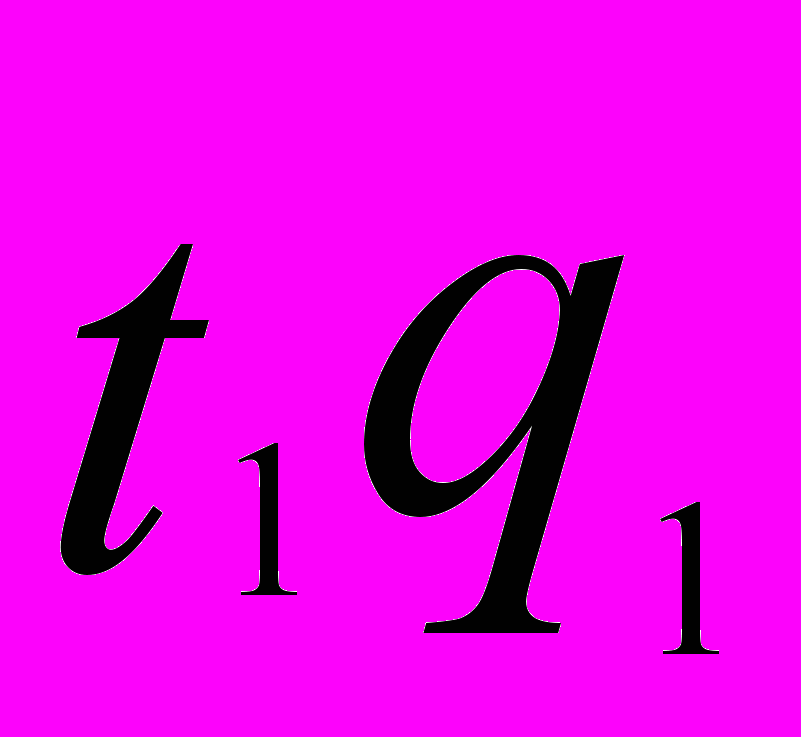





Изделие А

Изделие Б

Изделие В
1,0

1.2

0,9
0,9

1,0

0,8
458

311

765
450

324

752






Итого
--
--
--
--







По данным таблицам 7.2 рассчитать сводный индекс производительности.


Задание №3

Таблица 7.3

Реализация товаров в натуральном и стоимостном выражении

Товар
Реализация в базисном периоде, руб.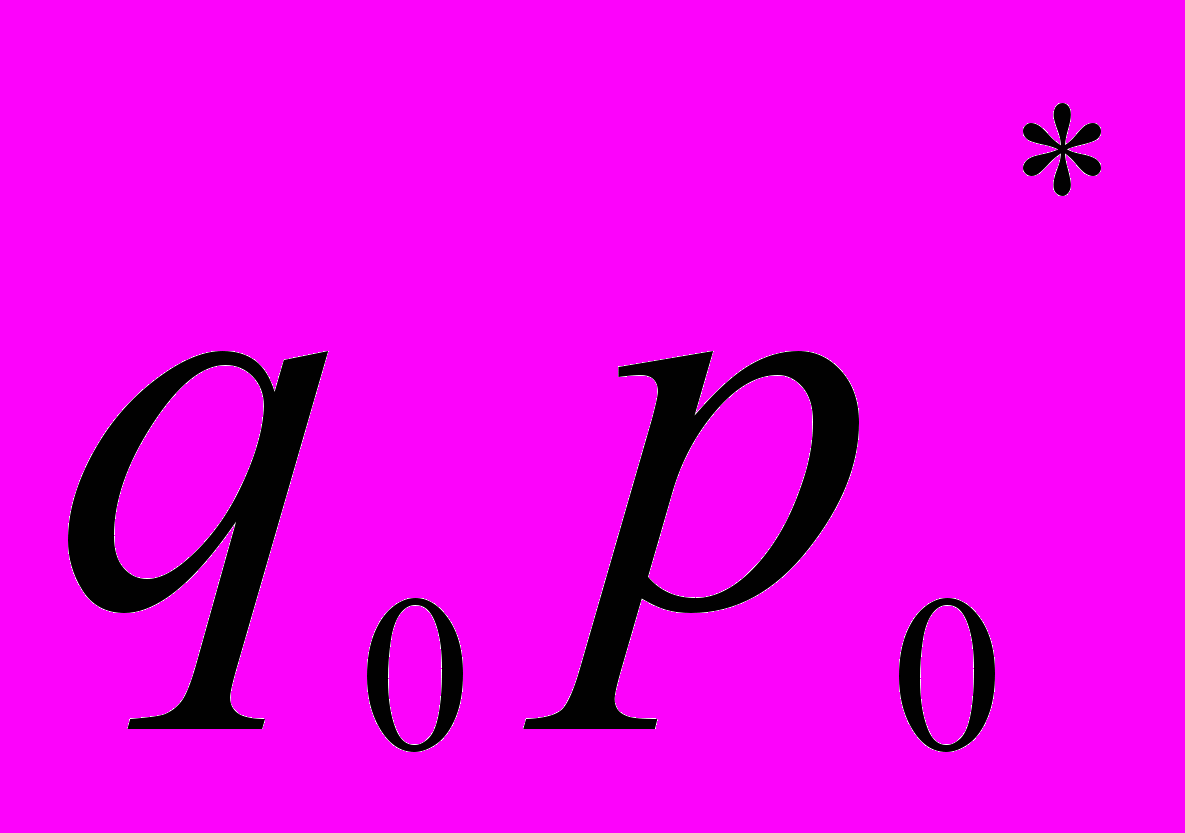
Изменение физического объема реализации в текущем периоде по сравнению с базисным, %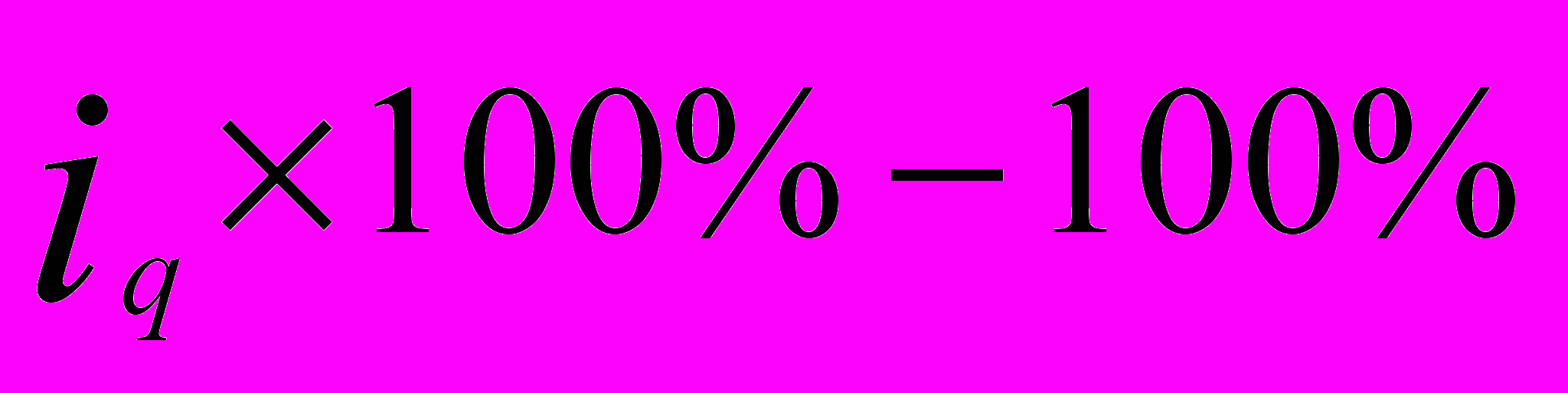
Расчетные графы





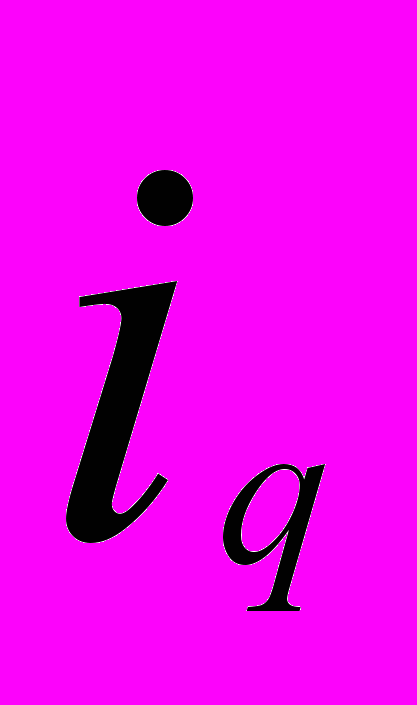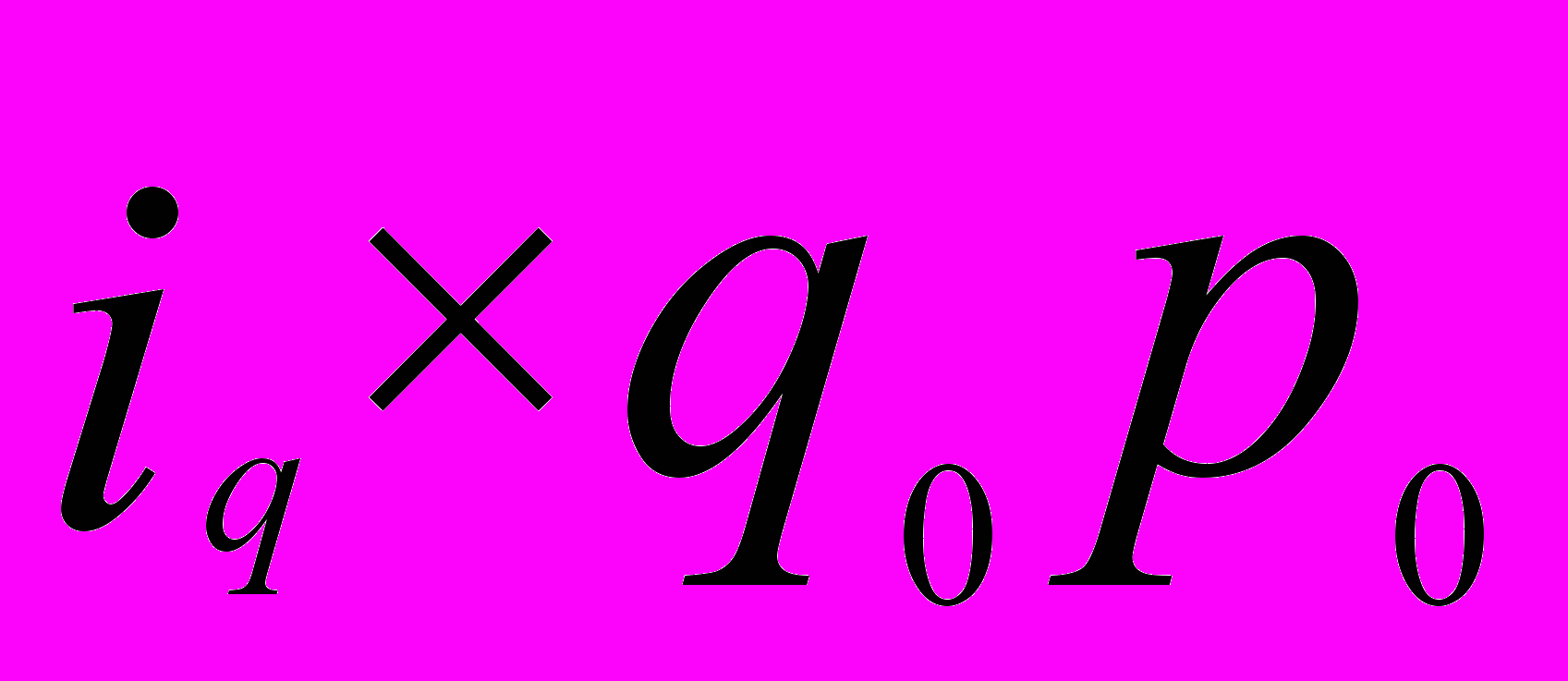Мандарины

Грейпфрукты

Апельсины
46000

27000

51000
-6,4

-8,2

+1,3






Итого



--
--




По данным таблицы 7.3 рассчитать средневзвешенный арифметический индекс физического объема. Сделать вывод.


Задание №4

Таблица 7.4

Реализация овощной продукции

Товар
Реализация в текущем периоде, руб.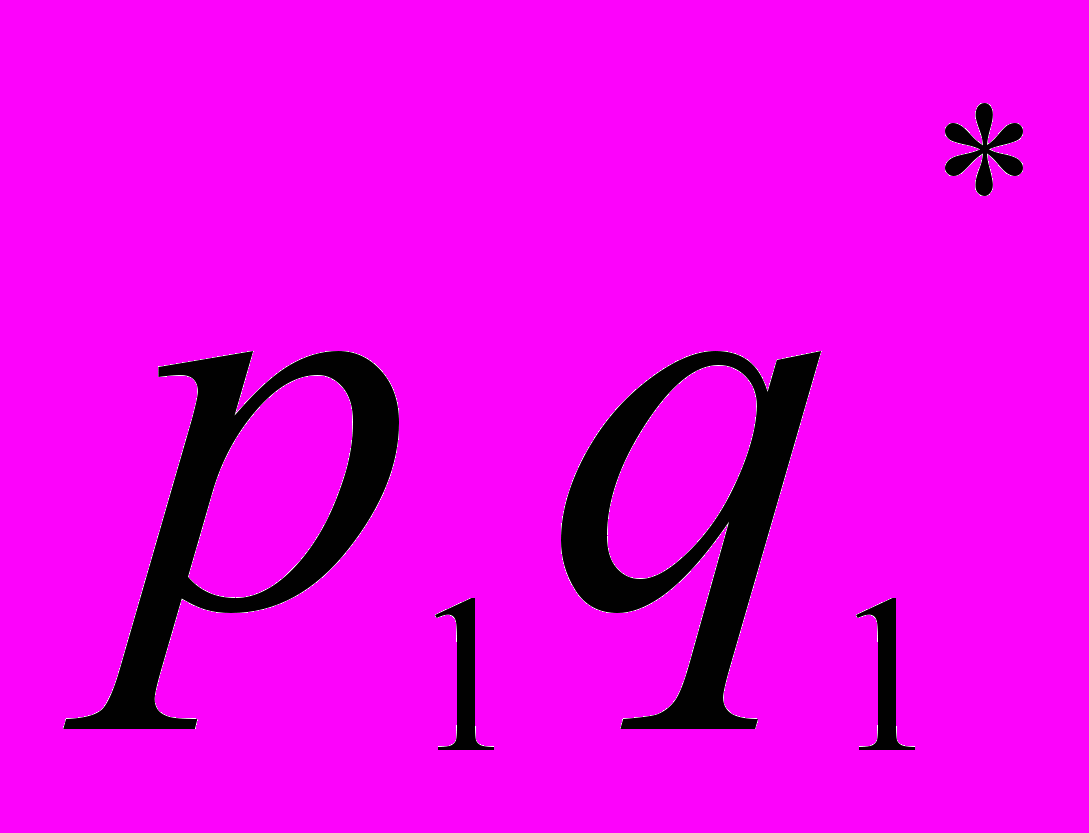
Изменение цен в текущем периоде по сравнению с базисным, %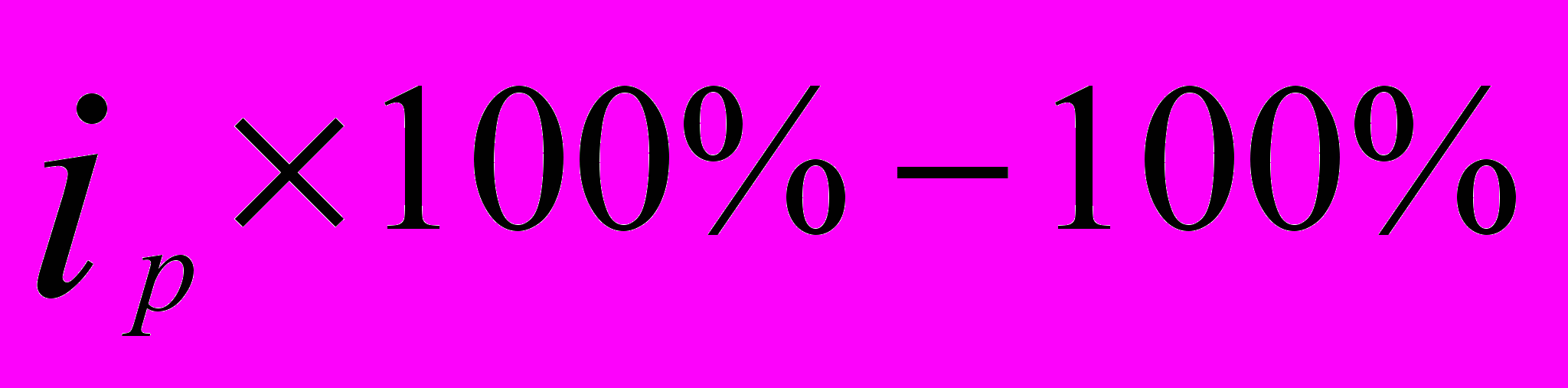
Расчетные графы





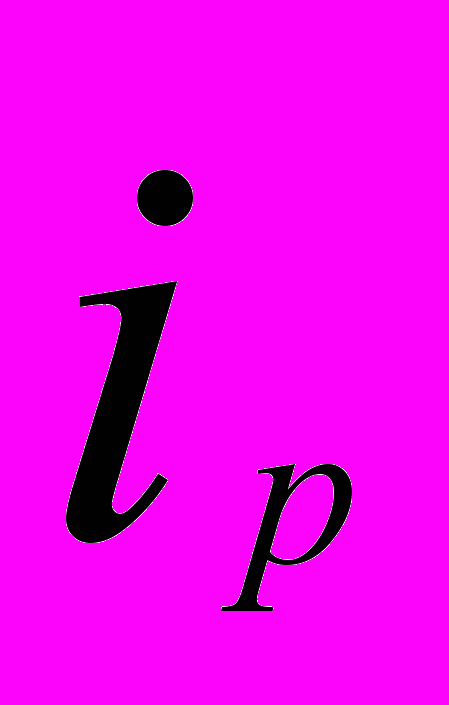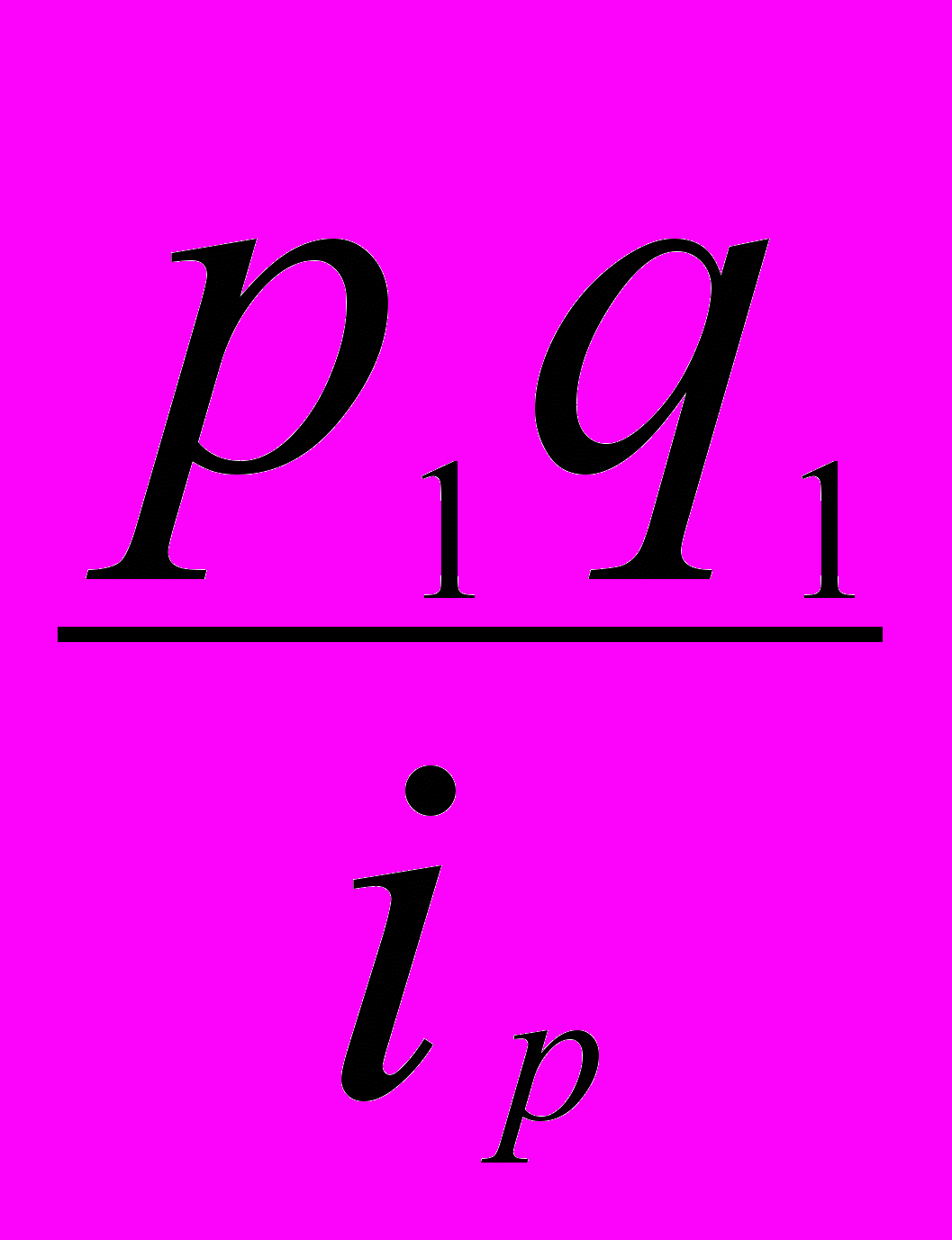Морковь

Свекла

Лук
23000

21000

29000
+4,0

+2,3

-0.8






Итого



--
--




По данным таблицам 7.4. вычислить средневзвешенный гармонический индекс цен.


Задание №5

Таблица 7.5

Изменение цен реализации товара в двух регионах

Регион
Июнь
Июль
Расчетные графы

Цена, руб.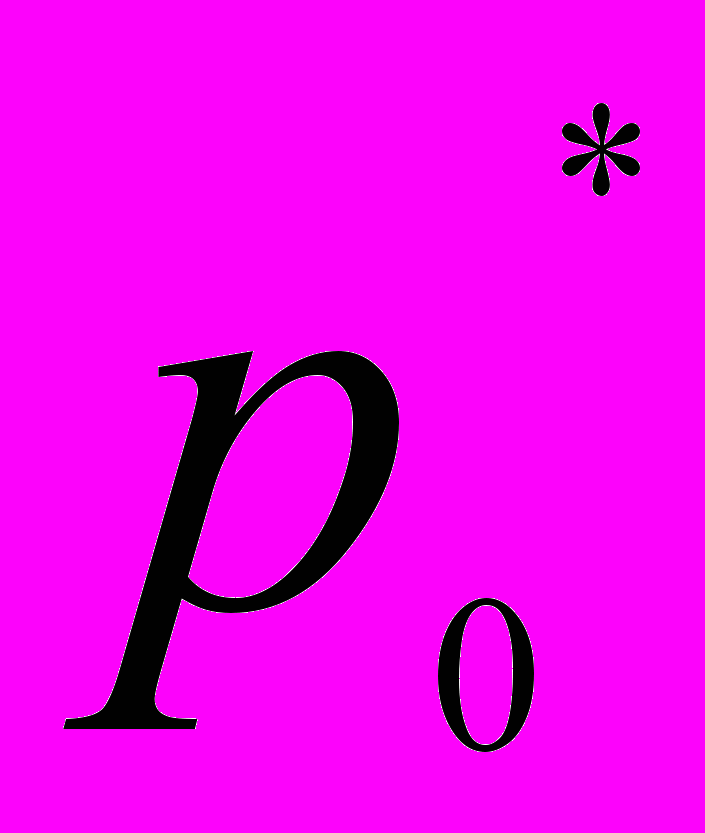

Продано, шт.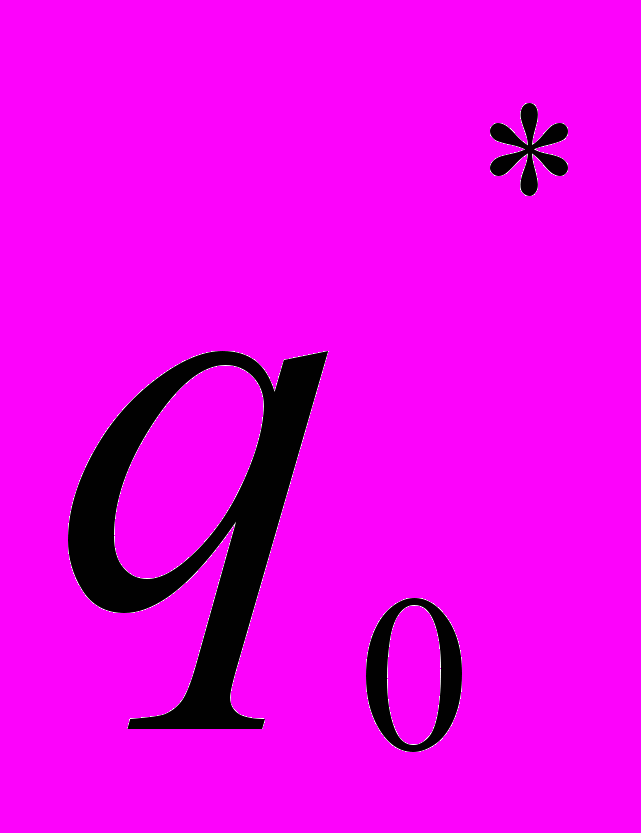
Цена, руб.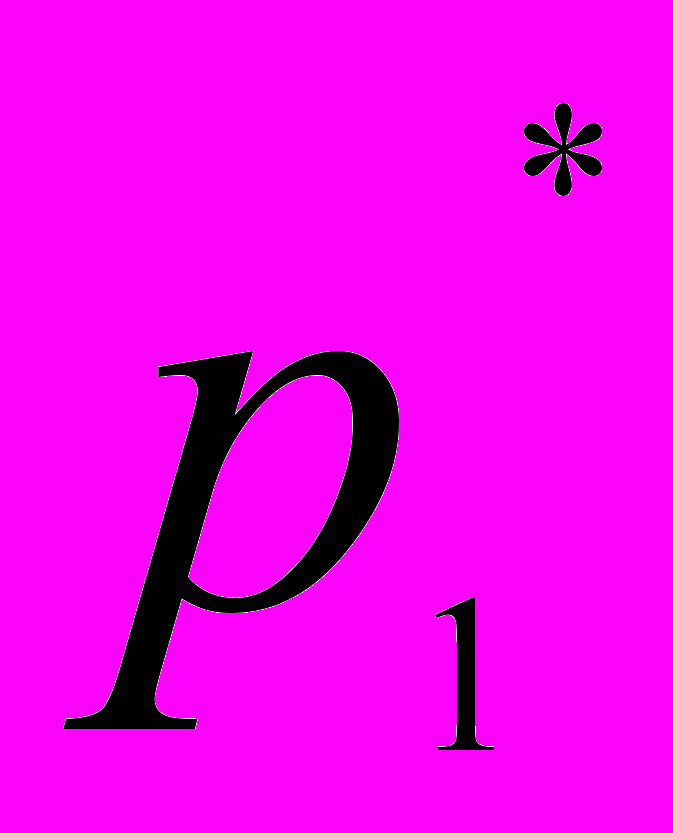
Продано, шт.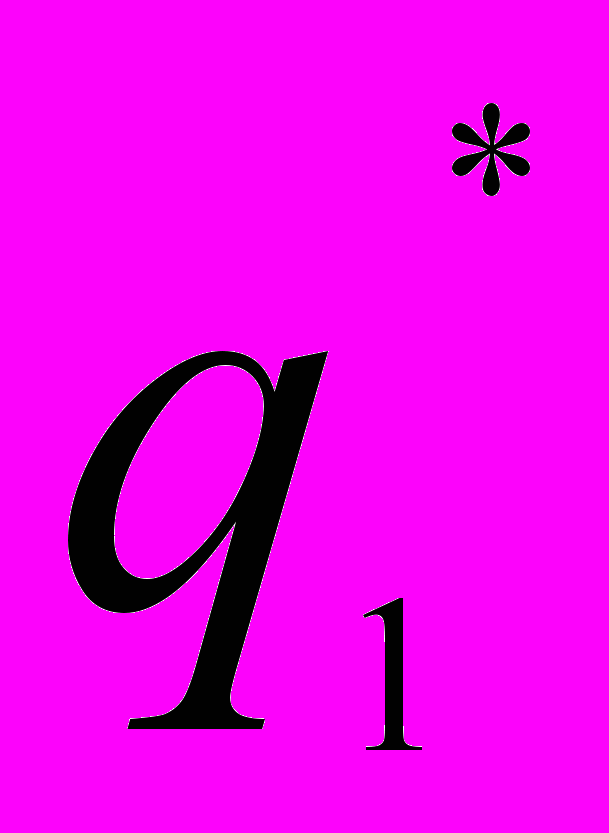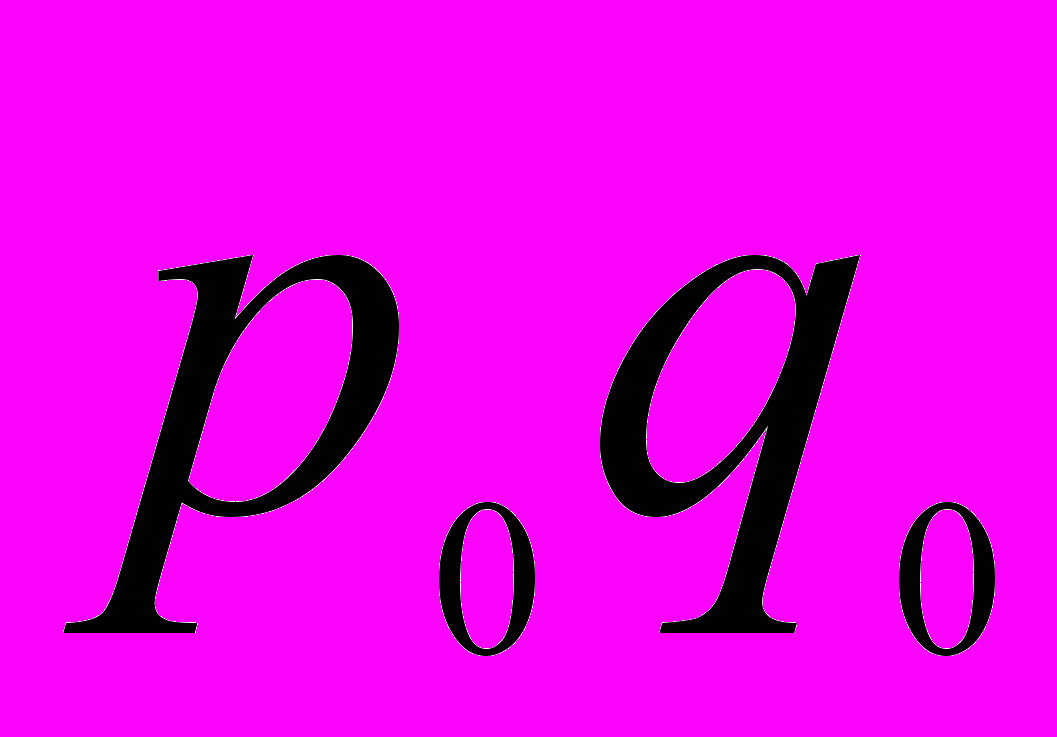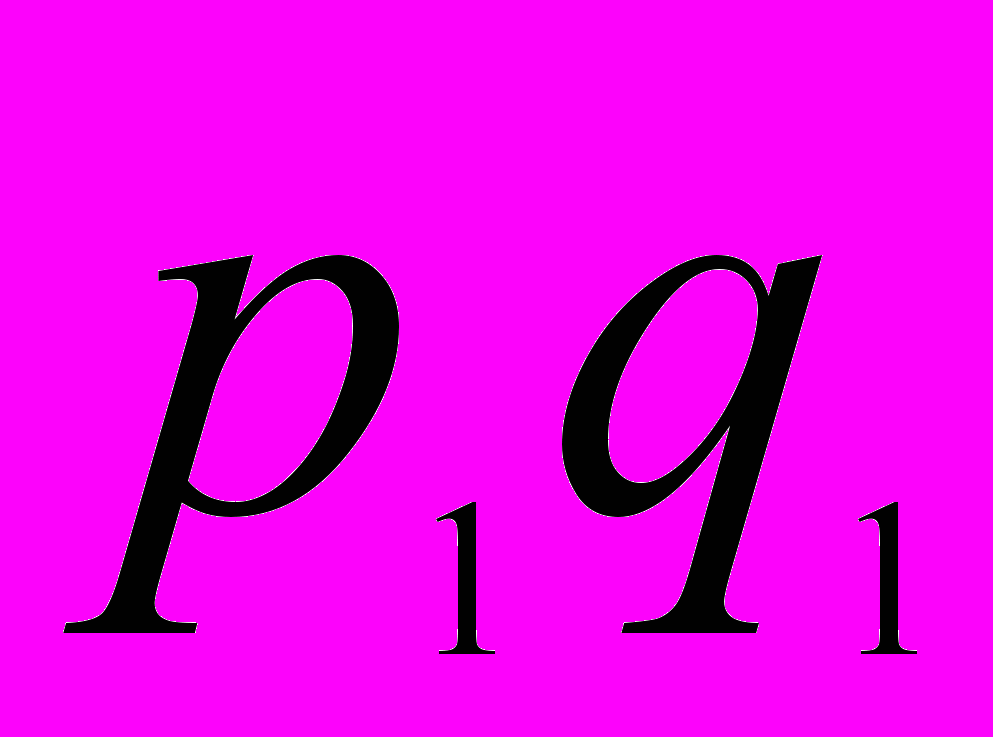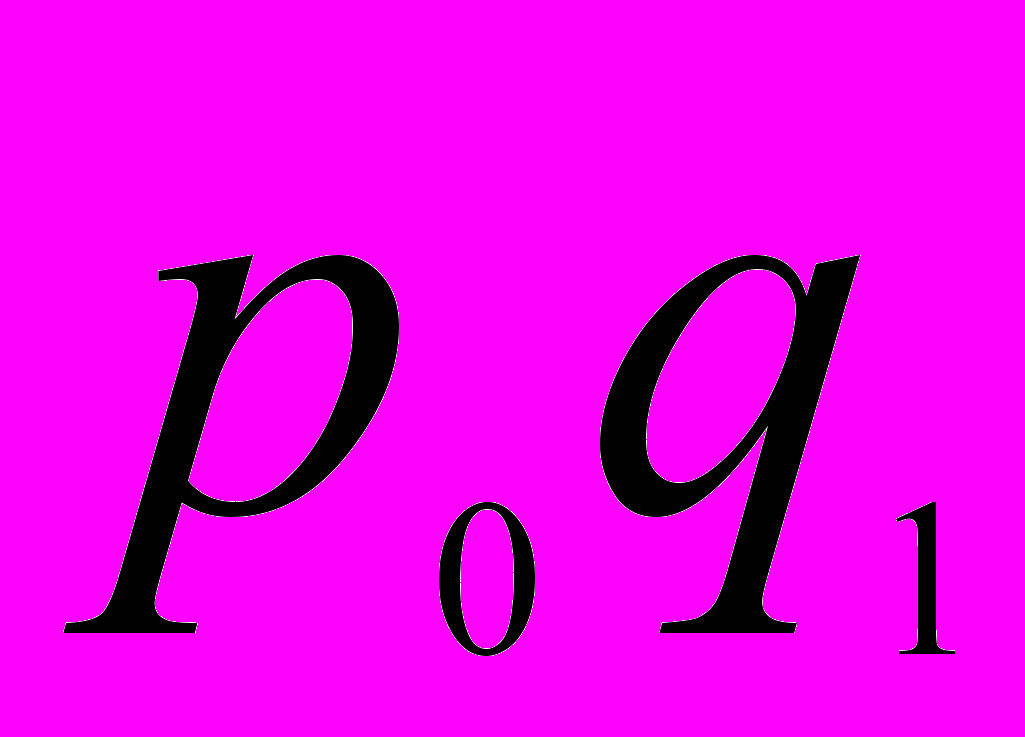






1

2
12

17
10000

20000
13

19
18000

9000









Итого

--



--