Geum.ru

Учебно-методический комплекс дисциплины «статистика» Направление 080100 «экономика»

Вид материалаУчебно-методический комплекс

Содержание


Раздел 3. показатели вариации
Подобный материал:
1   2   3   4   5   6   7


РАЗДЕЛ 3. ПОКАЗАТЕЛИ ВАРИАЦИИ


Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.

Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнооб­разных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Колеблемость отдельных значений характеризуют показатели вариации. Под вариацией в статистике понимают такие количественные изменения величины изучаемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают случайную и систематическую вариацию.

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, можно оценить, насколько однородной является совокупность.

Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скрывается за средними.

Основа показателей общая — оценка отклонений значений показателей элементов совокупности от средней.

Задание №1.

На основе данных таблицы 3.2, рассчитать размах вариации, среднее линейное отклонение, коэффициент осцилляции, линейный коэффициент вариации.

Таблица 3.1

Расчетная таблица

Стаж работы, лет, (хi)
Число учителей в % к итогу, (fi)
xifi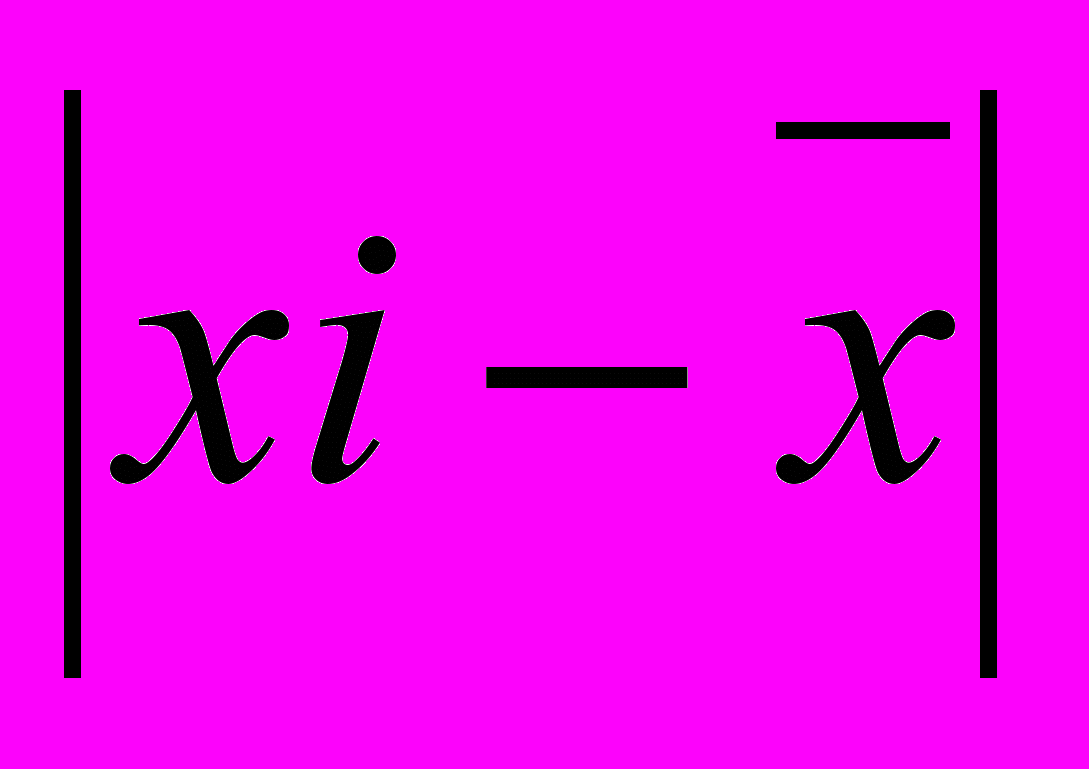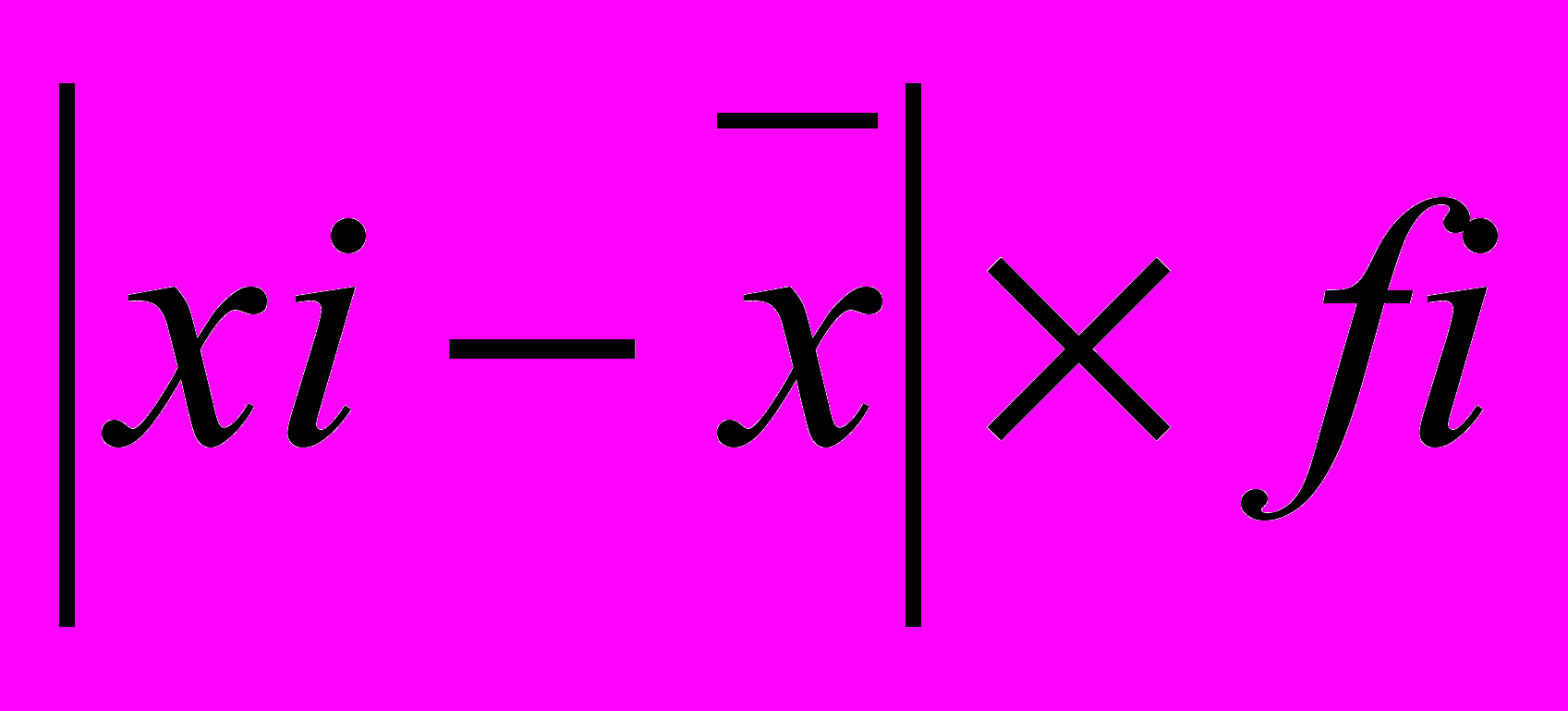















































































Итого






-



Таблица 3.2

Стаж работы учителей школы

Стаж работы, лет, (хi), (по вариантам)



№ варианта



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30



8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37



9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38



10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39



11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40



12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41



Продолжение таблицы 3.2



Число учителей в % к итогу(fi), (по вариантам)



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30



14
12
20
14
12
20
14
12
20
14
12
20
14
12
20
14
12
30
14
12
30
14
12
30
14
12
30
14
12
30



20
24
14
20
24
14
20
24
14
20
24
14
20
24
14
20
24
24
20
24
24
20
24
24
20
24
24
20
24
24



30
30
12
30
30
12
30
30
12
30
30
12
30
30
12
30
30
12
30
30
12
30
30
12
30
30
12
30
30
12



24
20
24
24
20
24
24
20
24
24
20
24
24
20
24
24
20
14
24
20
14
24
20
14
24
20
14
24
20
14



12
14
30
12
14
30
12
14
30
12
14
30
12
14
30
12
14
20
12
14
20
12
14
20
12
14
20
12
14
20



100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
Итог

Задание №2.

По данным таблицы 3.3 рассчитать дисперсию двумя способами, среднее квадратическое отклонение, коэффициент вариации.

Для нахождения дисперсии, среднего квадратического отклонения, коэффициента вариации использовать расчетную таблицу 3.4.

Таблица 3.3

Распределение магазинов города по товарообороту

Группы магазинов по величине товарооборота, млн.руб.
Число магазинов (fi), (по вариантам)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

40-50
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

50-60
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

60-70
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

70-80
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

80-90
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

90-100
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

100-110
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

110-120
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

120-130
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

130-140
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Продолжение таблицы 3.3

Группы магазинов по величине товарооборота, млн.руб.
Число магазинов (fi),(по вариантам)

16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

40-50
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

50-60
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

60-70
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

70-80
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

80-90
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

90-100
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

100-110
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

110-120
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

120-130
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

130-140
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32



Таблиц 3.4

Расчетная таблица

Группы магазинов по величине товарооборота, млн.руб.
Число магазинов

(fi)
Середина интервала, тыс.руб. (xi)
xifi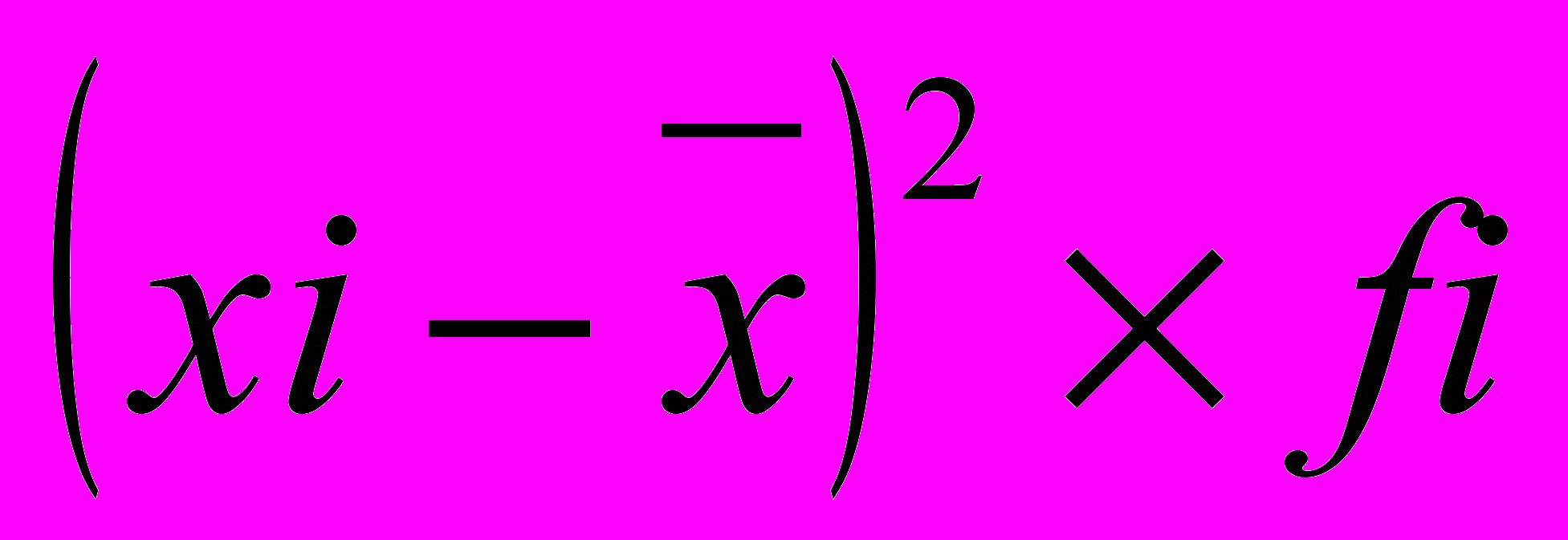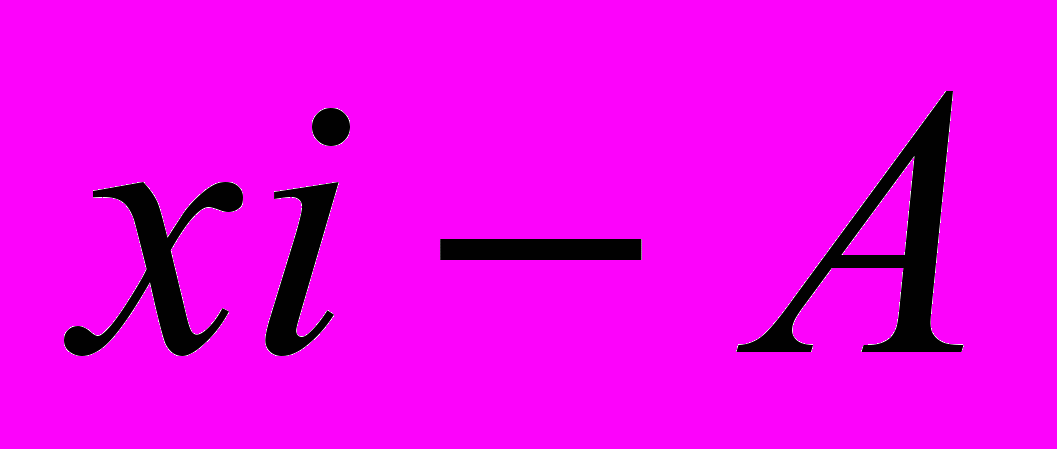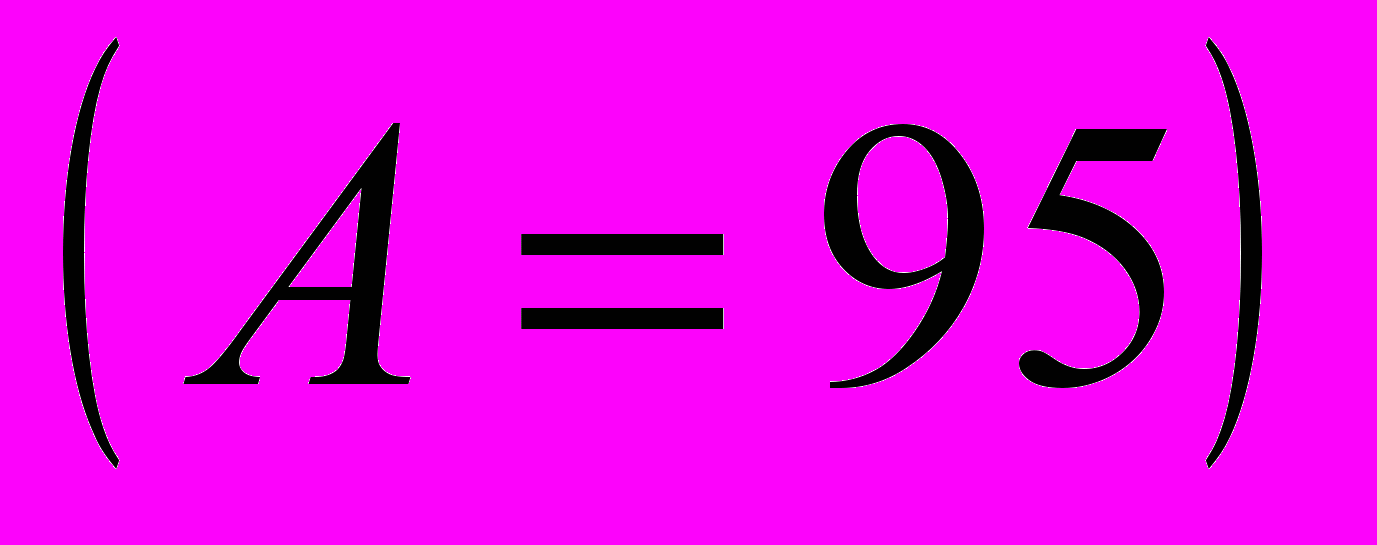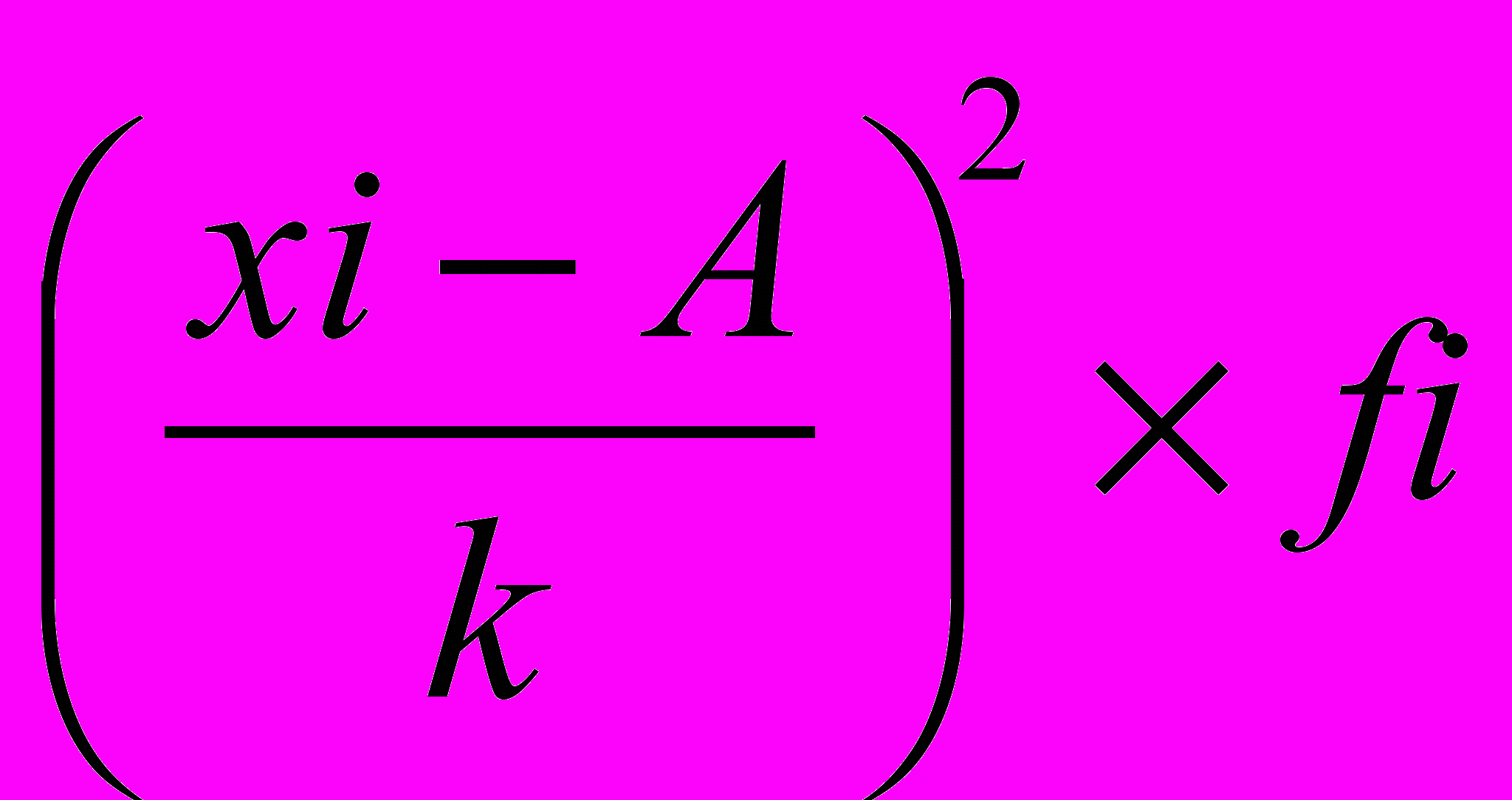








40-50


















50-60


















60-70


















70-80


















80-90


















90-100


















100-110


















110-120


















120-130


















130-140


















Итого