Geum.ru

Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материалаДокументы

Содержание


РАЗРАБОТКА ПРОГРАММНОГО КОМПЛЕКСА ДЛЯ РЕШЕНИЯ ЗАДАЧ КОНВЕКЦИИ-ДИФФУЗИИ Андреева Е.М.
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   75


РАЗРАБОТКА ПРОГРАММНОГО КОМПЛЕКСА ДЛЯ РЕШЕНИЯ ЗАДАЧ КОНВЕКЦИИ-ДИФФУЗИИ

Андреева Е.М.

Ростовский государственный университет, ЮГИНФО


andreeva@rsu.ru

Огромную роль в современной науке играет математическое моделирование. Сущность математического моделирования заключается в замене объектов и процессов реального мира их «образами» - математическими моделями и дальнейшем изучении модели с помощью реализуемых на компьютере вычислительно-логических алгоритмов. Такой подход сочетает в себе многие достоинства, как теории, так и практики.

Основу математического моделирования составляет триада: модель-алгоритм-программа. На первом этапе вычислительного эксперимента выбирается или строится модель исследуемого объекта. Второй этап связан с выбором или разработкой вычислительного алгоритма для реализации модели на компьютере. А на третьем этапе создается программное обеспечение. При создании адекватного вычислительному эксперименту программного продукта нужно учитывать важнейшую специфику математического моделирования, связанную с использованием ряда (иерархии) математических моделей, многовариантностью расчетов в рамках фиксированной математической модели. Это подразумевает широкое использование комплексов и пакетов прикладных программ, разрабатываемых, в частности, на основе объектно-ориентированного программирования. Здесь уже нельзя обойтись решением одного варианта программы на компьютере, необходимо иметь возможность легко менять входные параметры для многократного решения подобных задач.

Программное обеспечение вычислительного эксперимента базируется на использовании комплексов и пакетов прикладных программ. Комплекс программ предназначен для решения близких по своей математической природе задач из одной предметной области. Он включает в себя библиотеку программных модулей (в большей или меньшей степени независимых), из которых комплектуются рабочие программы. В комплексах прикладных программ сборка программ из модулей осуществляется вручную.

В пакетах прикладных программ для сборки используются системные средства компьютера, что позволяет в значительной степени автоматизировать этот процесс. Пакеты прикладных программ, рассматриваемые как технология решения задач в рамках вычислительного эксперимента, позволяют наиболее эффективно использовать накопленные программные продукты, резко поднять производительность труда программиста.

Затем в цикле вычислительного эксперимента проводится серия расчетов на компьютере при изменении тех или иных параметров задачи. Полученные данные могут представляться с помощью таблиц и графиков.

На этапе анализа результатов становиться ясным, удачно ли выбрана математическая модель, ее вычислительная реализация.

Моделирование различных процессов в движущихся средах приводит к необходимости решать уравнения конвекции - диффузии, содержащие первые производные. Если конвективные члены в уравнении преобладают, то это означает, что в задаче присутствует малый параметр. При аппроксимации таких задач методом конечных разностей или методом конечных элементов получаются системы линейных алгебраических уравнений (СЛАУ) с несимметричной матрицей, у которых норма несимметричной части значительно больше нормы симметричной ее части, то есть у СЛАУ отсутствует диагональное преобладание. Для решения такого класса задач необходимы специальные численные методы, поскольку большинство базовых итерационных методов для них не применимы. Данная работа посвящена созданию пакета прикладных программ, который позволит быстро и эффективно решать системы линейных алгебраических уравнений с сильно несимметричными матрицами, возникающими при аппроксимации задач, описываемых уравнениями математической физики.

Разработанный ППП включает два основных блока функциональную и сервисную части. Функциональная часть содержит итерационные методы решения СЛАУ с сильно несимметричными матрицами, которые будут использованы как сглаживатели в многосеточном методе. Сервисная часть пакета содержит модуль графического отображения полученных данных.

Комплекс предназначен для решения стационарной задачи конвекции-диффузии





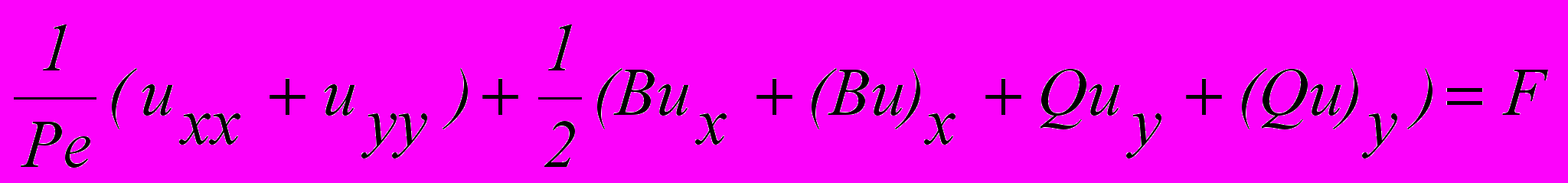
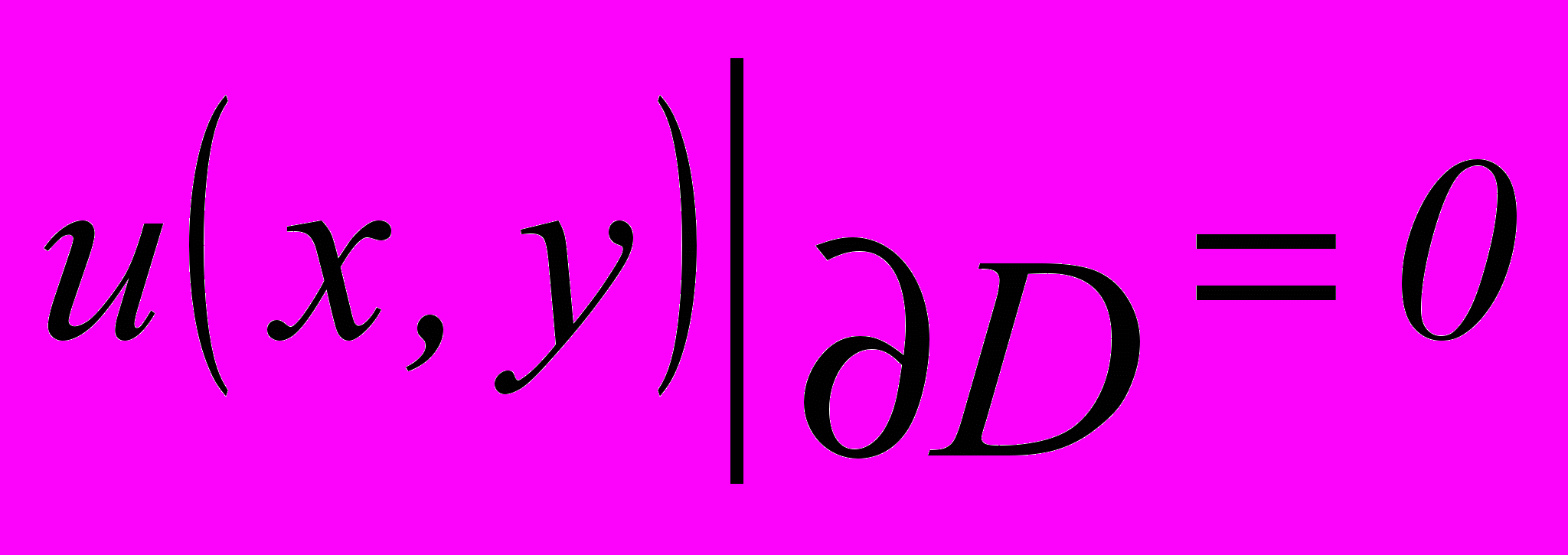
в области D=[0,1][0,1]. Для аппроксимации данного дифференциального уравнения используется метод конечных разностей с центрально-разностной аппроксимацией первых производных.

Комплекс позволяет решать полученную в результате аппроксимации СЛАУ с несимметричной диссипативной матрицей, используя треугольные кососимметричные итерационные методы, а так же многосеточный метод, в котором в качестве сглаживающей процедуры можно выбрать треугольные кососимметричные методы или стандартные сглаживатели (метод Гаусса-Зейделя, Якоби, Ричардсона). Особенностью треугольных методов является то, что они не требуют диагонального преобладания для исходной матрицы, что достигается специальным выбором итерационного оператора, использующего только кососимметричную часть исходной матрицы. Расчеты можно проводить на различных сетках, для различных малых параметров 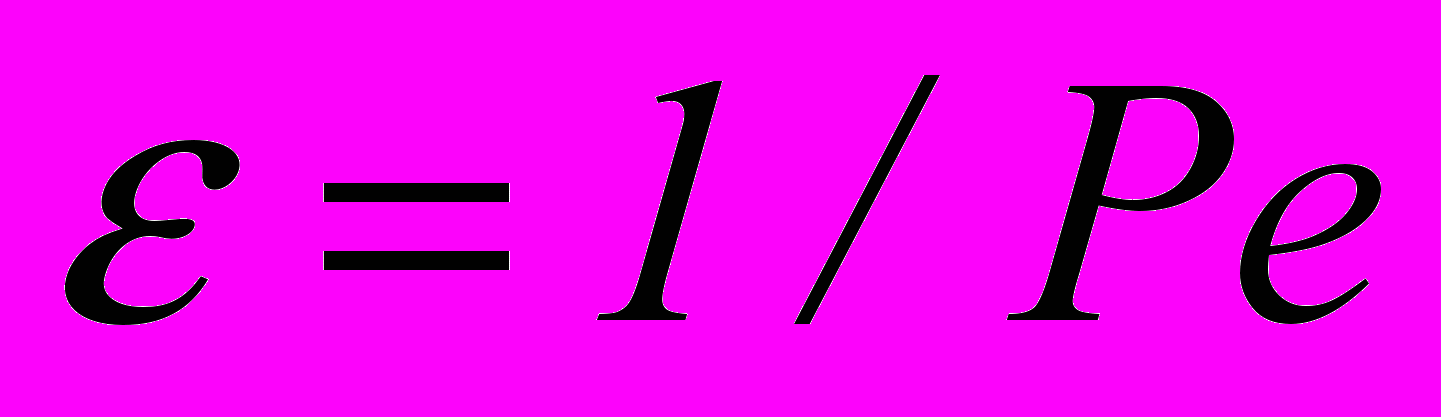, так же необходимо ввести итерационный параметр , вектор скорости движения среды и точное решение, для построения правой части решаемого уравнения.

При проведении численных экспериментов вектор скорости движения среды может задаваться с помощью постоянных, линейных, с разделяющимися переменными и быстроменяющихся коэффициентов.

При использовании многосеточного метода требуется указать сглаживающую процедуру и количество сглаживающих итераций.

С помощью выводимых данных пользователь получает возможность оценить эффективность применяемых методов для решения поставленной задачи. Для оценки эффективности сглаживающей процедуры многосеточного метода рассчитывается «величина сглаживания», введенная Хакбушем .

Созданный ППП может быть применен исследователями, изучающими процессы переноса тепла с большими числами Пекле, течения Навье-Стокса с большими числами Рейнольдса , задачи магнитной гидродинамики с большими числами Хартмана и др.

Для работы с конкретным прикладным пакетом пользователь должен изучить состав функционального наполнения ППП и класс решаемых с его помощью задач, правила работы с пакетом, язык запросов.

Эти требования создают трудности в освоении и использовании прикладного пакета, особенно для пользователей-непрограммистов. Большую помощь в упрощении использования данного пакета может оказать диалоговый интерфейс между пользователем и программным обеспечением пакета. Диалог позволяет самостоятельно ставить и решать «стандартные» задачи из предметной области пакета.