Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материала

Документы

Содержание МНОГОУРОВНЕВЫЙ ЭЛЕКТРОННЫЙ УЧЕБНИК ПО КУРСУ ЧИСЛЕННЫХ МЕТОДОВ Жуков М.Ю., Пацеева Е.В., Петровская Н.В., Ширяева Е.В., Цывенкова

Подобный материал:

• Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
• Программа 1-3 октября 2003 года Москва Организаторы и спонсоры Министерство образования, 141.3kb.
• Министерство образования и науки российской федерации федеральное агентство по образованию, 32.48kb.
• Российской Федерации Читинский государственный университет иппк рабочая программа, 177.68kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 39.54kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 60.77kb.
• Министерство образования и науки российской федерации тамбовский государственный университет, 59kb.
• Министерство образования и науки российской федерации российский государственный социальный, 183.27kb.
• Н. А. Быковой Контрольные вопросы, 24.48kb.
• Министерство образования и науки российской федерации программ, 381.21kb.

МНОГОУРОВНЕВЫЙ ЭЛЕКТРОННЫЙ УЧЕБНИК ПО КУРСУ ЧИСЛЕННЫХ МЕТОДОВ

Жуков М.Ю., Пацеева Е.В., Петровская Н.В., Ширяева Е.В., Цывенкова О.А.

Ростовский государственный университет,механико-математический факультет

heli@math.rsu.ru

Комплекс программ «Электронный учебник по численным методам» состоит из набора учебно-демонстрационных программ, а также электронных текстов. В настоящее время в учебнике имеются темы «Теория погрешности», «Интерполяция полиномами», «Численное интегрирование», «Линейная алгебра» и его структура позволяет без труда добавлять новые разделы. Каждая тема сопровождается программой, текстом лабораторной работы и тестом для проверки (или самопроверки) знаний.

Электронный учебник может использоваться как для проведения практических занятий на физико-математических факультетах университетов, так и для самостоятельного углубленного изучения соответствующих численных методов.

Комплекс программ разработан в среде Delphi. Тексты лабораторных работ и тестов созданы при помощи пакета MikTeX. Для своего использования учебник требует ОС Windows9x/2000/XP и установленную на компьютере программу Adobe Acrobat Reader.

Комплекс программ имеет дружественный, интуитивно-понятный интерфейс, поддерживает работу с мышью и клавиатурой, обеспечивает корректную обработку ошибок во время выполнения. Реализованы дополнительные возможности для управления форматом текстового и графического выводов, а также сохранения графической информации в файлы формата bmp, а текстовой информации — в файлы в форматах rtf и txt.

Важная отличительная особенность данного учебника заключается в том, что помимо чтения текста, что с успехом можно сделать и по обычному учебнику, пользователь имеет возможность в любой момент вызвать из имеющихся программных модулей тот, который даст ему возможность проследить все детали процесса применения изучаемого метода.

Каждая тема электронного учебника снабжена лабораторной работой, которая содержит необходимый теоретический материал для освоения изучаемой темы, а также тексты заданий для проведения практикума. Варианты заданий ориентированы на их выполнение с помощью пакета Maple, одной из прикладных программ, входящих в электронный учебник и какой-либо среды программирования. В качестве базового языка при выполнении заданий лабораторных работ выбран язык Pascal. В лабораторной работе имеется набор программных кодов, которыми студенты могут пользоваться как образцами при самостоятельном программировании.

Электронный учебник снабжен тестами, позволяющими проводить проверку полученных знаний. Тесты представлены в двух вариантах: первый — выбор правильного ответа из имеющегося набора; второй — вариант, в котором требуется проводить некоторые вычисления.

Предлагаемый набор тестов позволит пользователю оценить уровень своих знаний, понять, какие именно вопросы наиболее важны при изучении темы. Очень быстро пользователь убедится, что на первый взгляд просто демонстрационные программы позволяют ему проводить самостоятельную исследовательскую работу, т.е. использовать их как инструмент для научной работы в других областях знаний.

В демонстрационно-обучающих программах, входящих в электронный учебник, реализованы следующие численные методы:

7. Тема «Вычислительная погрешность»: метод прямой и обратной задачи теории погрешностей.
   
8. Тема «Интерполяция полиномами»: метод Лагранжа; методы Ньютона для равноотстоящих и неравноотстоящих узлов; линейная интерполяция: кубический сплайн;
   
9. Тема «Численное интегрирование»: методы прямоугольников, метод трапеций, метод Симпсона, методы Гаусса, метод Эрмита, правило Рунге.
   
10. Тема «Линейная алгебра»: варианты метода Гаусса, метод квадратного корня, различные итерационные методы.
    

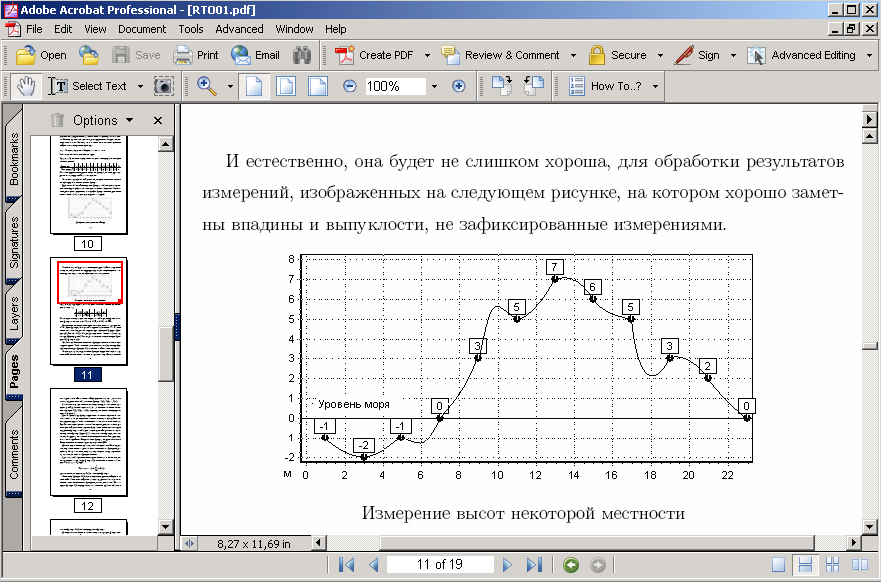
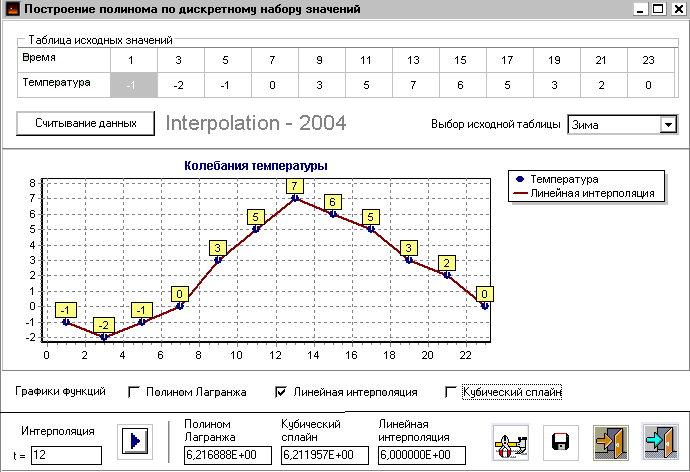
Рис.1 Рис.2


На Рис.1–6 изображены этапы работы по теме «Интерполяция». На Рис.1 приведена страница лабораторной работы с постановкой задачи. На Рис.2 представлен рабочий момент взаимодействия с программой – ввод начальных данных и графическая иллюстрация простейшего типа интерполяции.




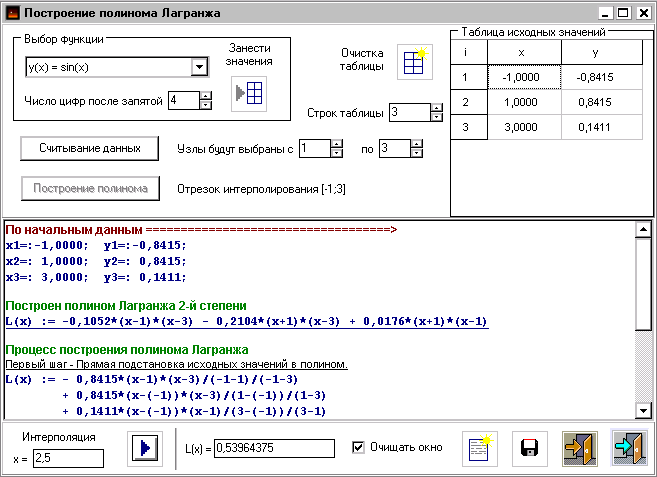
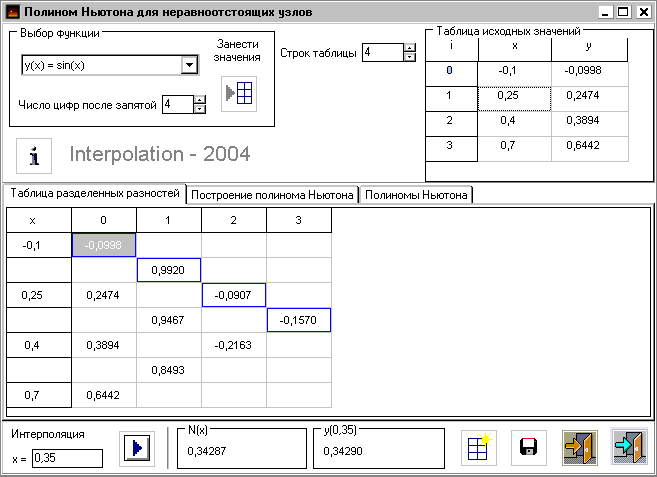
^{Рис.3 Рис.4}


На Рис.3 и 4 приведены рабочие окна, предназначенные для построения интерполяционного многочлена в форме Лагранжа (слева) и Ньютона (справа). Рис.5 и 6 иллюстрируют работу с интерактивными тестами по той же теме.


Рис.5 Рис.6


Учебник тестировался (и в процессе тестирования улучшался) при проведении занятий на механико-математическом факультете и факультете высоких технологий по темам «Интерполяция полиномами» и «Численное интегрирование» (преп. Ширяева Е.В.). В результате его использования удалось существенно повысить понимание и усвояемость студентами курса методов вычислений.

Работа выполнена при поддержке ректората РГУ в 2004 году в рамках конкурса по развитию и внедрению информационных технологий в процесс обучения. Авторы выражают благодарность сотруднику ЮГИНФО Ткачевой Л.А. за терпение и внимательное отношение к авторам работы.