В. Д. Никифорова > В. Ю. Островская государственные и муниципальные ценные бумаги учебное пособие

Вид материала

Содержание

P по отношению к рыночной ставке r
4.2. Доходность и ликвидность государственных ценных бумаг.
К, принесет продавцу дополнительный доход. И, наоборот, в случае, если цена будет меньше К
НКД на момент заключения сделки купли/продажи: CF - НКД = N + CF – P ( P –
YTM от ставки реинвестирования купонных платежей, рассмотренной выше. Поэтому, показатель YTM
N - номинал выпуска, руб., P

Подобный материал:

1 ... 5 6 7 8 9 10 11 12 ... 15

Взаимосвязь дюрации с показателями n, k и YTM позволяет сделать ряд важных выводов:

- дюрация облигации с нулевым купоном всегда равна сроку ее погашения, т.е.: при k = 0, D = n;

- дюрация купонной облигации всегда меньше срока погашения: при k > 0, D < n;

- с ростом рыночной доходности (процентной ставки на рынке) дюрация купонной облигации уменьшается и, наоборот, со снижением рыночной доходности дюрация купонной облигации увеличивается.

Показатель дюрации, или средней продолжительности, более корректно учитывает особенности временной структуры потока платежей, поскольку в нем отдаленные платежи имеют меньший вес, и, следовательно, оказывают меньшее влияние на результат, чем более близкие к моменту оценки. Иногда дюрацию интерпретируют как точку равновесия сроков дисконтированных платежей.

При этом следует иметь в виду, что основное назначение дюрации состоит в том, что она характеризует чувствительность цены облигации к изменениям процентных ставок на рынке (доходности к погашению). Используя дюрацию, таким образом, можно управлять инвестиционным риском, связанным с изменением процентных ставок.

В общем случае, процентный риск облигации может быть измерен показателем эластичности ее цены P по отношению к рыночной ставке r. Пусть r = YTM, тогда эластичность EL можно определить по формуле:

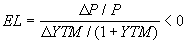(4.1.11)

Поскольку между ценой облигации и ее доходностью к погашению существует обратная зависимость величина EL будет всегда отрицательной. Тогда из формулы (4.1.11) следует, что:

(4.1.12) .

Применив дифференцирование можно показать, что:

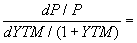
(4.1.13)

Откуда:

(4.1.14) .

Из (4.1.13) и (4.1.14) следует, что EL = D и дюрация характеризует эластичность цены облигации к изменениям ее доходности.

Преобразуем правую часть математического соотношения 4.1.14 следующим образом:

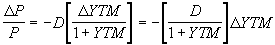(4.1.15)

Величина, заключенная в квадратные скобки, получила название модифицированной дюрации (modified duration – MD):

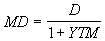(4.1.16) Тогда:

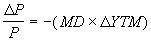(4.1.17)

Формулу (4.1.17) нередко используют для определения изменения цены облигации исходя из предполагаемого изменения доходности к погашению.

Завершая рассмотрение свойств дюрации, кратко остановимся на недостатках, присущих данному показателю. Первое ограничение вытекает из нелинейной формы связи между YTM и Р. Поскольку скорость изменения показателей при этом будет разной, применение показателей D или MD для прогнозирования цен облигаций в случае значительных колебаний процентных ставок будет приводить к преувеличению падения курса при росте YTM или некоторому занижению реального роста курса при уменьшении YTM.

Другим существенным недостатком дюрации как меры измерения процентного риска является неявное допущение независимости доходности от срока погашения. Таким образом, предполагается, что краткосрочные процентные ставки изменяются также, как и долгосрочные. Например, если доходность по 3-х месячным ГКБО изменилась на 1%, то и доходность 15-летних ОВВЗ также должна измениться на 1%. Однако, не реалистичность подобного допущения очевидна.

Для устранения причин проблем, возникающих при использовании дюрации, является нелинейность взаимосвязи между ценой и доходностью, может быть использована вторая производная функции в качестве характеристики ценового риска (4.1.18):

(4.1.18)

С математической точки зрения, значение данного показателя представляет собой скорость изменения дюрации при изменении доходности к погашению YTM. Нетрудно заметить, что численное значение второй производной зависит от величины купонного платежа c_t, срока обращения Т и доходности YTM. Поскольку для купонных облигаций, в большинстве случаях, c_t = const и срок погашения Т известен заранее, главный интерес представляет зависимость от YTM. Как следует из формулы выпуклости, числовое значение второй производной уменьшается с ростом YTM и, наоборот, оно растет с уменьшением YTM. Таким образом, выпуклость является объяснением сформулированного выше правила асимметричного изменения цен при одинаковом изменении доходности (величина роста курса всегда больше, чем величина падения). Запишем формулу в следующем виде:

. (4.1.19)

Разделив на Р, получим количественное измерение степени крутизны (выпуклости) кривой "цена-доходность":

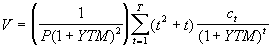. (4.1.20)

Из приведенных формул следует, что выпуклость прямо зависит от срока погашения Т и дюрации соответственно. Можно также отметить, что выпуклость является возрастающей функцией от функции дюрации. В целом, свойства выпуклости по отношению к Т и k аналогичны свойствам дюрации.

Вместе с тем, выпуклость связана положительной зависимостью с изменениями рыночных процентных ставок (доходности к погашению). Объяснение этого свойства следует из того факта, что выпуклость можно определить как разность между фактической ценой облигации и ее ценой, определенной с использованием модифицированной дюрации.

Совместное использование дюрации D и выпуклости V при анализе инвестиций в облигации с фиксированным доходом позволяет существенно повысить точность оценки изменений их стоимости. Вместе с тем, их совместное использование требует соответствующей формализации.

Один из подходов к решению данной проблемы базируется на аппроксимации изменения цены облигации с помощью рядов Тейлора. При этом, степенной ряд будет иметь следующий вид:

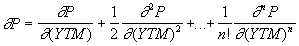(4.1.21)

Ограничимся рассмотрением первых двух элементов ряда. Разделив обе части на Р, имеем:

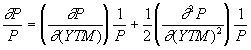(4.1.22)

Первое слагаемое теперь является дюрацией D, а второе – выпуклостью V, умноженной на константу. С учетом вышеизложенного, более эффективную формулу для определения будущей цены облигации в зависимости от изменений доходности можно задать в следующем виде:

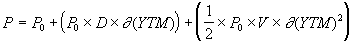(4.1.23) , где

Р – будущая цена при условии, что доходность изменится на величину ∂(YTM); Р₀ – текущая цена; D – дюрация; V – выпуклость.

Результаты сравнительного анализа точности прогнозирования цены 15-летней ОВВЗ седьмого транша с годовым купоном 3% при рыночной норме доходности 9% в зависимости от изменений доходности к погашению с использованием дюрации и полученной математической модели с D и V приведены в следующей таблице 4.1.2.:

Таблица 4.1.2.

∂(YTM)	YTM	Реальная цена (P)	Прогноз цены (модель с D )		Прогноз цены (модель с D и V )
			P	Отклонение	Р	Отклонение
-0,04	0,05	79,24068	72,46125	6,779	77,95719	1,2835
-0,03	0,06	70,86325	67,25594	3,607	70,3474	0,5158
-0,02	0,07	63,56834	62,05062	1,518	63,42461	0,1437
-0,01	0,08	57,20261	56,84531	0,357	57,18881	0,0138
0	0,09	51,64	51,64	0,000	51,64	0,0000
0,01	0,10	46,75744	46,43469	0,323	46,77818	0,0207
0,02	0,11	42,47304	41,22938	1,244	42,60336	0,1303
0,03	0,12	38,70222	36,02406	2,678	39,11553	0,4133
0,04	0,13	35,37621	30,81875	4,557	36,31469	0,9385

Отметим, что добавлением в математическую модель элементов ряда Тейлора более высокого порядка можно добиться еще большей точности прогноза, несмотря на то, что их доля в общем изменении стоимости облигации достаточно мала.

Нередко методы фундаментального анализа рынка дополняется техническим анализом, приемы которого также достаточно разнообразны. Использование сигналов нескольких индикаторов, или методик прогноза (200- дневного скользящего среднего значения, осцилляторов и др.), увеличивает вероятность принятия оптимальных решений в отношении инвестиций в облигации.

4.2. Доходность и ликвидность государственных ценных бумаг.

Доход по купонным облигациям имеет две составляющие: периодические выплаты и курсовая разница между рыночной ценой и номиналом. Поэтому такие облигации характеризуются несколькими показателями доходности: купонной, текущей (на момент приобретения) и полной (доходность к погашению).

Купонная доходность задается при эмиссии облигации и определяется соответствующей процентной ставкой. Ее величина зависит от двух факторов: срока облигационного займа и надежности (кредитоспособности) эмитента.

Чем больше срок погашения облигации, тем выше ее риск, следовательно, тем больше должна быть норма доходности, требуемая инвестором в качестве компенсации. Не менее важным фактором является надежность эмитента, определяющая кредитный рейтинг облигации. Государство считается наиболее надежным заемщиком, поэтому ставка купона у облигаций федерального займа обычно ниже, чем у облигаций субъектов РФ, муниципалитетов или корпоративных. Корпоративные облигации считаются наиболее рискованными.

Купонная доходность при фиксированной ставке известна заранее и остается неизменной на протяжении всего срока обращения, однако, если облигация покупается (продается) в момент времени между двумя купонными выплатами, важнейшее значение при анализе доходности, как для продавца, так и для покупателя, приобретает производный от купонной ставки показатель – величина накопленного процентного (купонного) дохода (НКД) к дате покупки/продаже облигации (accrued interest). Для того, чтобы торговая операция была выгодной для продавца, величина купонного дохода должна быть поделена между участниками сделки, пропорционально периоду хранения облигации между двумя выплатами. Причитающаяся участникам сделки часть купонного дохода может быть определена по формуле обыкновенных, либо точных процентов. Накопленный купонный доход на дату сделки купли/продажи можно определить по формуле:

(4.2.1) , где

CF – купонный платеж; t – число дней от начала периода купона до даты продажи (покупки); N – номинал; k – ставка купона; m – число выплат в год; В = {360, 365 или 366} – используемая временная база (360 для обыкновенных процентов; 365 или 366 для точных процентов).

Рассчитанное значение представляет собой часть купонного дохода, на которую будет претендовать в данном случае продавец. Свое право на получение части купонного дохода (т.е. за период хранения) он может реализовать путем включения величины НКД в цену облигации. Если предположить, что облигация была приобретена продавцом по номиналу, тогда курс продажи облигации, обеспечивающий получение пропорциональной сроку хранения части купонного дохода может быть определен по формуле: К = (N + НКД) / 100.

Продажа облигации по цене, превышающей К, принесет продавцу дополнительный доход. И, наоборот, в случае, если цена будет меньше К, продавец понесет убытки, связанные с недополучением части купонного дохода исходя из срока хранения облигации. Соответственно часть купонного дохода, причитающаяся покупателю за оставшиеся дни хранения облигации до выплаты купонного дохода, может быть определена двумя способами.

Первый способ предусматривает осуществление расчетов с учетом величины НКД на момент заключения сделки купли/продажи: CF - НКД = N + CF – P ( P – цена покупки). Второй способ включает в расчет определение НКД с момента приобретения до даты платежа по облигации. Нетрудно заметить, что определенная таким образом цена (К) соответствует ситуации равновесия, когда и покупатель, и продавец, получают свою долю купонного дохода. Однако, не исключено, что в отдельные дни ситуация на рынке облигаций может складываться в пользу продавцов, либо покупателей.

Текущая доходность (current yield – Y) облигации с фиксированной ставкой купона определяется как отношение периодического платежа к цене приобретения:

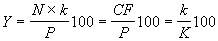(4.2.2) .

Текущая доходность продаваемых облигаций меняется в соответствии с изменениями их рыночных цен. Однако с момента покупки она становится постоянной (зафиксированной) величиной, так как ставка купона остается неизменной. Очевидно, что текущая доходность облигации приобретенной с дисконтом будет выше купонной, а приобретенной с премией – ниже.

В то же время показатель текущей доходности не учитывает вторую составляющую дохода от облигации, а именно: курсовую разницу между ценой покупки и погашения (как правило – номиналом). Поэтому этот показатель не может применяться для сравнения доходности инвестиций в облигации с различными исходными условиями.

В качестве меры общей эффективности (доходности) инвестиций в облигации используется показатель доходности к погашению (yield to maturity – YTM). Доходность к погашению представляет собой процентную ставку (норму дисконта), устанавливающую равенство между текущей стоимостью потока платежей по облигации PV и ее рыночной ценой P.

Для облигаций с фиксированным купоном, выплачиваемым раз в году, она определяется путем решения следующего уравнения:

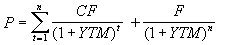(4.2.3.) ,

где F – цена погашения (как правило, F = N).

Уравнение (4.2.3) решается относительно YTM каким-либо итерационным методом. Приблизительное значение этой величины можно определить из соотношения (4.2.4):

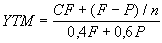(4.2.4) .

По сути, доходность к погашению YTM представляет собой внутреннюю норму доходности инвестиции (internal rate of return – IRR). Тем не менее, реальная доходность облигации к погашению будет равна YTM только при выполнении следующих условий: во-первых, облигация хранится до срока погашения; во-вторых, полученные купонные доходы сразу же реинвестируются по ставке r = YTM.

Очевидно, что независимо от желаний инвестора, второе условие достаточно трудно выполнить на практике. В нижеприведенной таблице даны результаты расчета доходности к погашению облигации, приобретенной в момент выпуска по номиналу в 1000 руб. с погашением через 20 лет и ставкой купона 8%, выплачиваемого раз в год, при различных ставках реинвестирования.

Таблица 4.2.1.

Зависимость доходности к погашению от ставки реинвестирования

Ставка реинвестирования r	Купонный доход за 20 лет	Общий доход по облигации за 20 лет	Доходность к погашению YTM
0%	1600,00	1600,00	4,84%
6%	1600,00	3016,00	7,07%
8%	1600,00	3801,00	8,00%
10%	1600,00	4832,00	9,01%

Из расчетов следует, что с уменьшением r будет уменьшаться и величина YTM; с ростом r величина YTM будет также расти. На величину показателя YTM оказывает влияние и цена облигации. При этом, здесь имеется обратная зависимость. В итоге, можно сформулировать общие правила, отражающие взаимосвязи между ставкой купона k, текущей доходностью Y, доходностью к погашению YTM и рыночной ценой облигации Р:

если P > N, k > Y > YTM;

если P < N, k < Y < YTM;

если P = N, k = Y = YTM.

Руководствуясь данными правилами, не следует забывать о зависимости YTM от ставки реинвестирования купонных платежей, рассмотренной выше. Поэтому, показатель YTM более правильно трактовать как ожидаемую доходность к погашению.

Несмотря на присущие ему недостатки, показатель YTM является одним из наиболее популярных измерителей доходности купонных облигаций, применяемых на практике. Его значения приводятся во всех публикуемых финансовых сводках и аналитических обзорах.

Доходность по ОФЗ с переменным купоном рекомендуется определять по формуле (4.2.5):¹

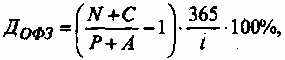где N– номинал облигации, руб.; Р– цена облигации, руб.; С – величина купона, руб.; А – накопленный с начала купонного периода доход (НКД), руб.; t – срок до окончания текущего купонного периода, дней.

Облигации с неизвестным (переменным) купонным доходом дают его владельцам право на периодическое получение процентного (купонного) дохода. При этом, здесь возможно также получение дисконта, если цена приобретения облигаций (при первичном размещении или на вторичных торгах) будет меньше цены их реализации, в том числе при погашении облигаций по их номиналу.

По ОФЗ-ПК размеры каждого купона объявляются непосредственно перед началом соответствующего купонного периода исходя из текущей доходности выпусков ГКБО, которые погашаются примерно в одно время с датой выплаты этого купона. Общая формула доходности к погашению по формуле сложных процентов выглядит следующим образом:

(4.2.6), где: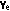

— эффективная доходность к погашению (в процентах годовых, с точностью до сотых процента), которая определяется из приведенной выше формулы численными методами;

— номинал облигации (руб.);

— цена облигации (руб.);

— величина накопленного купонного дохода (руб.);

— размер i-того купона (руб.);

_________________________

¹ В соответствии с письмом Центробанка РФ от 5 октября 1995 г. № 28-7-3/А-693.

— количество предстоящих выплат купона;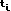

— число дней до выплаты соответствующего купона;

— срок до погашения облигации (в днях). Как правило, ;

— количество ближайших известных купонов;

— оценка неизвестных купонов, полученная по той же методике, по которой определяется размер купона.

В день объявления купона по ОФЗ-ПК осуществляется Центробанком РФ следующий расчет:

1) по выпускам ГКБО, которые погашаются в интервале ±30 дней от даты выплаты купона и которые обращались в течение четырех торговых сессий, непосредственно предшествовавших дню объявления купона, рассчитывается доходность (по каждой из четырех торговых сессий, непосредственно предшествовавших дню объявления купона). В качестве цены используется средневзвешенная цена выпуска ГКО на соответствующих вторичных торгах);

2) на основе рассчитанных показателей доходности определяется средневзвешенная доходность (веса — обороты по соответствующим выпускам ГКБО в рублях);

3) данная доходность (в процентах годовых) переводится в рублевое измерение с учетом длительности купонного периода. Полученное, таким образом, значение объявляется в качестве размера купона.

Доходом по бескупонным облигациям выступает дисконт, т.е. разница между ценой реализации (при погашении эта цена равна номиналу облигаций) и ценой их приобретения при первичном размещении или вторичном рынке. Для расчета доходности ГКБО могут использоваться следующие показатели:

– минимальная цена аукциона (цена отсечения), начиная с которой удовлетворяются конкурентные заявки на аукционе;

– средневзвешенная цена, равная отношению оборота ГКБО к суммарному количеству облигаций, участвующих в сделках.

Центробанком РФ была предложена методика расчета доходности ГКБО к погашению, согласно которой различают простую и эффективную доходность ГКБО к погашению.¹

Простая доходность ГКБО к погашению отражает доход от вложений в данные облигации в годовом измерении при условии их нахождения у инвестора до погашения:

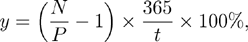(4.2.7) , где

N - номинал выпуска, руб., P – текущая рыночная цена, руб., t - срок до погашения выпуска, дней.

В качестве цены облигации Р могла быть использована средневзвешенная цена аукциона, либо цена последней сделки на торгах, по которым рассчитывался соответствующий показатель. Таким образом, данный показатель характеризует эффективность инвестирования средств в ГКБО на аукционе или вторичных торгах с учетом того, что инвестор держит облигации до их погашения.

В случае реализации ГКБО на вторичных торгах до срока их погашения расчет доходности к аукциону данных облигаций мог быть выполнен по формуле:

Р 365

Ya = ﴾ ----- - 1 ﴿ * ------ * 100 (4.2.8.) , где

Ра t

Р – цена облигаций в % к номиналу; Рa – средневзвешенная цена аукциона в % к номиналу; t – количество дней, прошедшее со дня аукциона.

Эффективная доходность ГКБО к погашению отражает эффективность вложений в данные облигации в годовом измерении при условии их нахождения у инвестора до погашения и реинвестирования в аналогичный инструмент основного долга и дисконтного дохода:

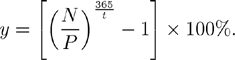(4.2.9).

_____________________________

¹ см. письмо № 28-7-3/А-693.

По сообщениям ИА «Рейтер» Минфин РФ прогнозирует снижение средневзвешенной доходности по облигациям государственного внутреннего займа в 2003 г. до 13,50% годовых (в 2002 г. - 14,81% годовых), что достаточно существенно, учитывая, что 75% их рынка составляют среднесрочные и долгосрочные ценные бумаги. Федеральный бюджет РФ на 2003 год предусматривает размещение краткосрочных облигаций федерального займа исходя из доходности в пределах 9-11%, долгосрочных - 13-14%.
в условиях инфляция 10-12% по сравнению с 12-14% в 2002 году.

Наряду с доходностью важнейшим показателем эффективности рынка является его ликвидность. При этом «короткие» выпуски ГКБО/ОФЗ рассматриваются участниками рынка в основном как средство управления текущей ликвидностью своих портфелей, что делает ставки по указанным облигациям более волатильными на интервале не более месяца.

Учитывая заинтересованность государства в увеличении дюрации долга, снижении стоимости его обслуживания, актуальным способом насыщения рынка «короткими» инструментами представляется организация раздельного обращения купонов и номиналов своих облигаций (так называемая программа STRIPS). Реализация программы STRIPS (далее – «стриппинг) позволяет Минфину РФ, не увеличивая реального объема государственного внутреннего долга и не сокращая сроков его обслуживания, производить долгосрочные заимствования, одновременно с этим предлагая участникам рынка краткосрочные инструменты. В итоге расширения спектра инструментов, обращающихся на рынке государственных облигаций, более привлекательным становится рынок, что способствует повышению его ликвидности.

Кроме того, для поддержания ликвидности участников в настоящее время на рынке государственных облигаций торговой системой совместно с Центробанком РФ предпринимаются усилия по организации полного спектра операций репо (биржевого модифицированного репо, междилерского репо и др.).

С другой стороны, снижение ставок заимствования и повышение ликвидности государственных облигаций позволяет их эмитентам осуществлять заимствование на внутреннем рынке на более выгодных условиях и направлять привлеченные средства на досрочный выкуп еврооблигаций, снижая тем самым расходы на обслуживание и погашение внешнего долга.

Blog

В. Д. Никифорова > В. Ю. Островская государственные и муниципальные ценные бумаги учебное пособие

Содержание