Geum.ru

Лекция № Тема 4: Линейная (не)зависимость. Ранг матрицы

Вид материалаЛекция

Содержание


З адача 5.1.в).
З адача 5.2.а).
З адача 5.2.в).
З адача 5.2.г).
Подобный материал:

Стр. из 5

Л
екция № 5.

Тема 4: Линейная (не)зависимость. Ранг матрицы.

Теорема Кронекера-Капелли.


Вспоминая вычисление определителей 2-го и 3-го порядков (вспомните!), убеждаемся, что определитель n-го порядка представляет собой сумму n! слагаемых, каждое из которых есть произведение n сомножителей -элементов матрицы, по одному из каждой строки и каждого столбца.


Мы уже умеем решать (с помощью обратной матрицы и по формулам Крамера) систему уравнений с квадратной основной матрицей, если ее определитель не равен нулю. А что делать, если он таки равен 0? И вообще, при каких условиях определитель равен 0?


З

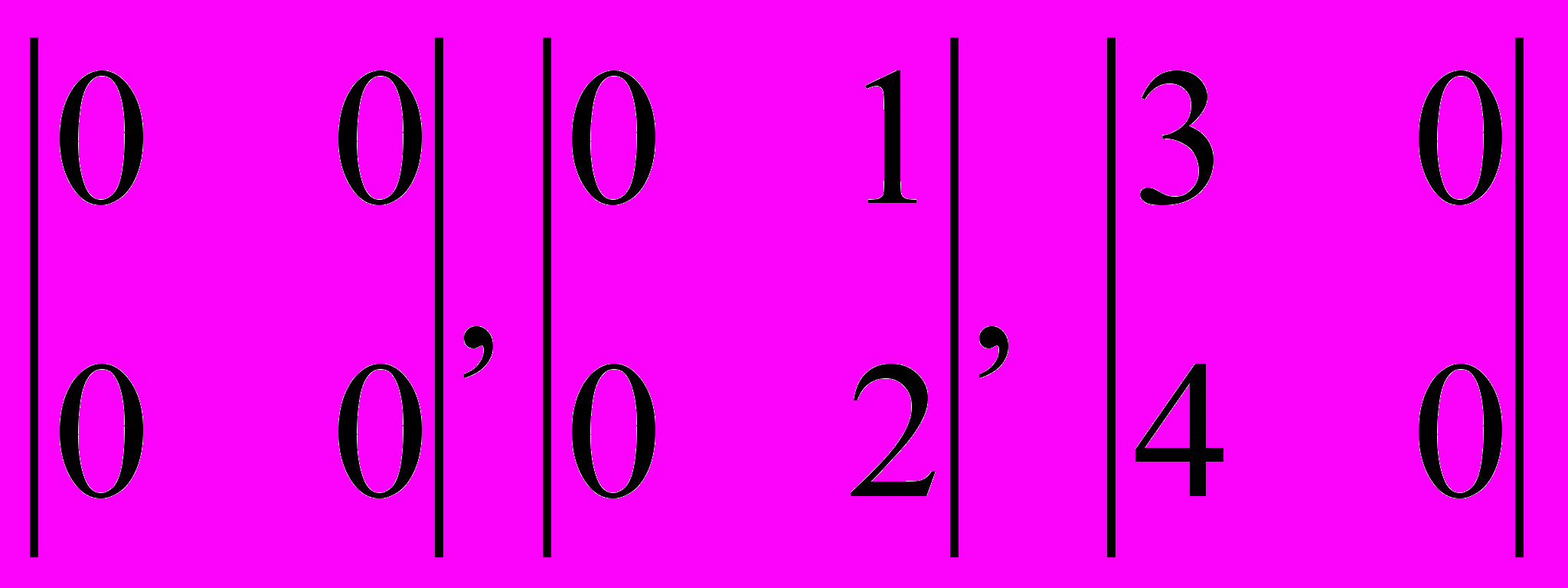
адача 5.1.а).

Вычислить определители:


Вычислите!


? Вопрос: Какое свойство определителей Вы можете сформулировать?

Напишите это свойство здесь: …..

…..


Далее некоторые части текста напечатаны белым шрифтом.

Начало и окончание каждой части выделены белым шрифтом на черном фоне.


Свойство 1. Если какой-либо столбец определителя равен 0, то определитель равен 0.


? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какой-либо его столбец равен 0?

Напишите здесь ответ с обоснованием: …..

…..

З

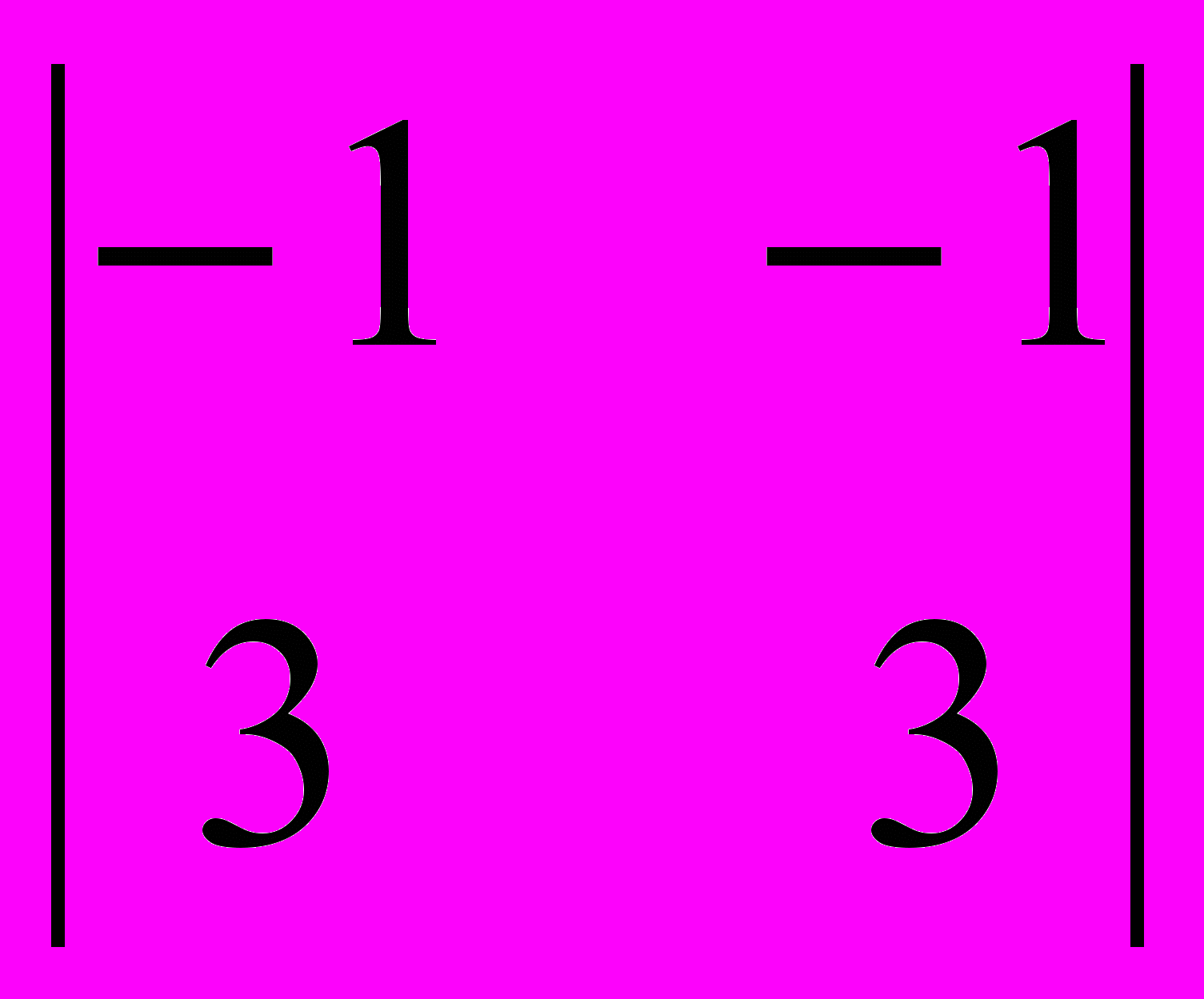
адача 5.1.б).

Вычислить определитель:


В

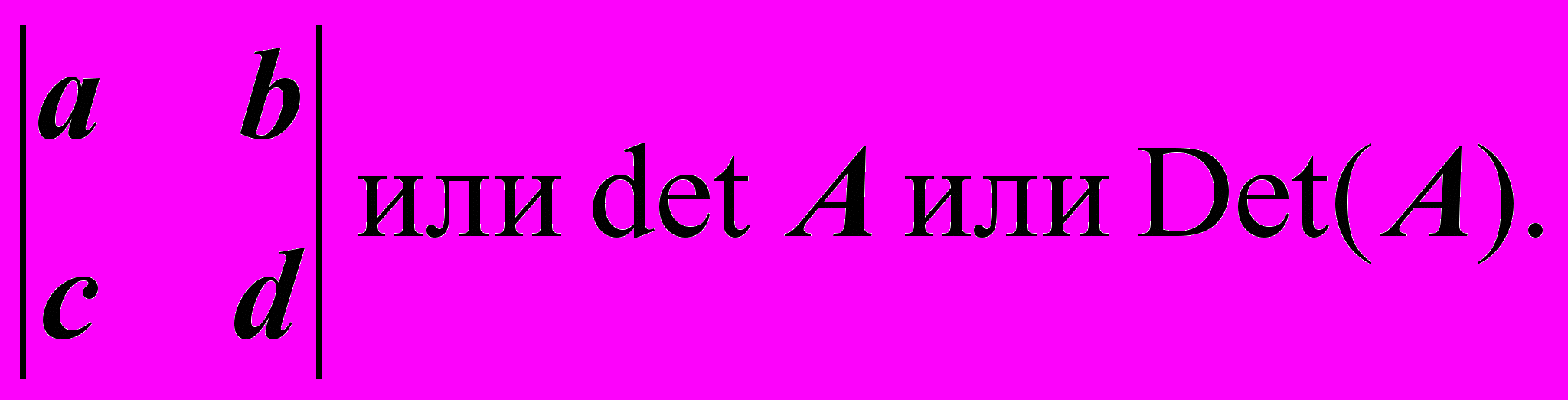
ычислите!


Как видим, определитель может быть равен нулю, а при этом ни один из его столбцов нулю не равен.


? Вопрос: Какое еще свойство определителей Вы можете сформулировать?

Напишите это свойство здесь: …..

…..

Свойство 2. Если какие-либо два столбца определителя равны друг другу, то определитель равен 0.

? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какие-либо два его столбца равны друг другу?

Напишите здесь ответ с обоснованием: …..

…..


З

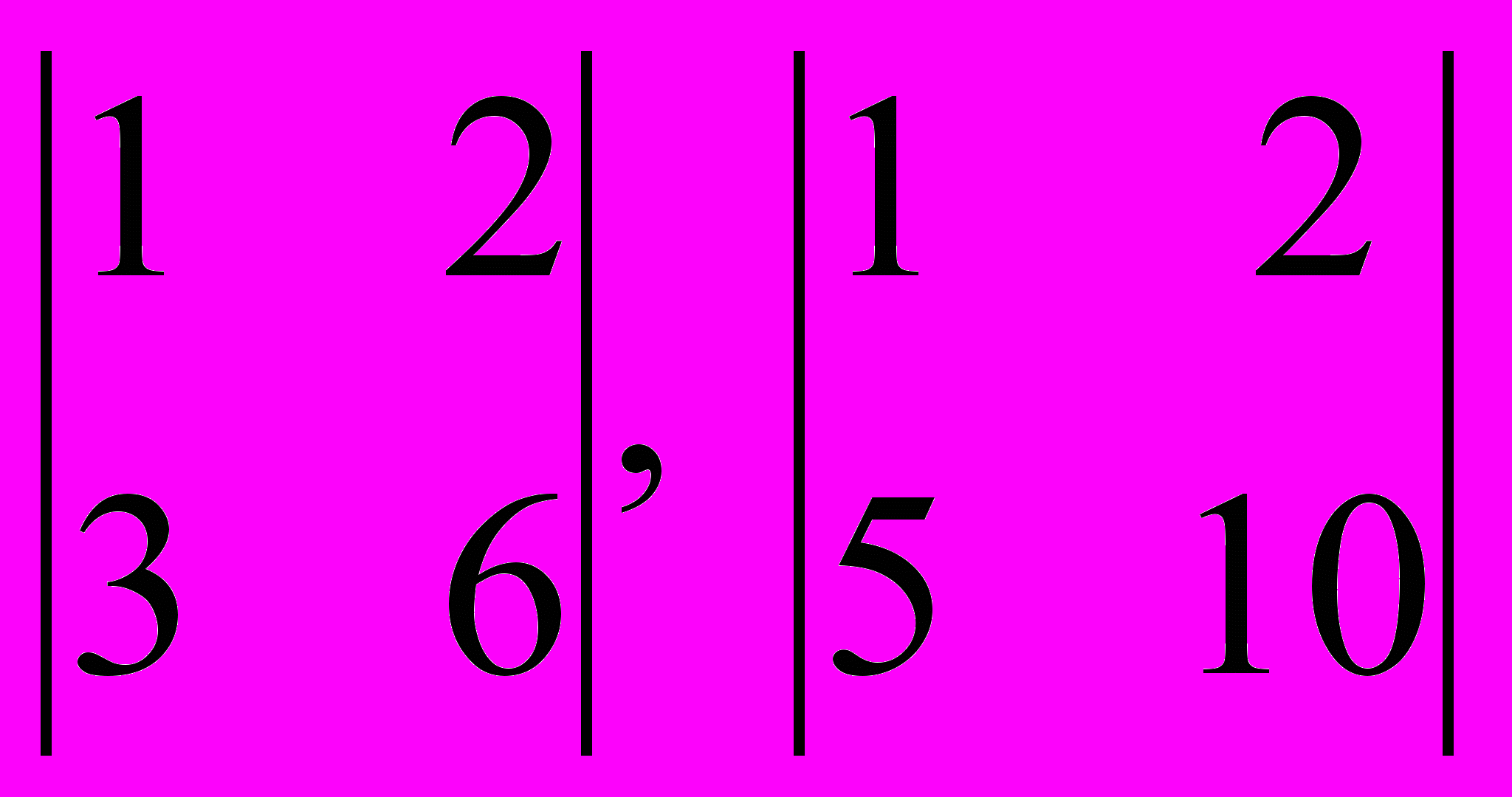
адача 5.1.в).

Вычислить определители:


Вычислите!


Как видим, определитель может быть равен нулю, а при этом его столбцы не равны друг другу.


? Вопрос: Какое еще свойство определителей Вы можете сформулировать?

Напишите это свойство здесь: …..

…..

Свойство 3. Если какие-либо два столбца определителя пропорцилнальны, то определитель равен 0.

? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какие-либо два его столбца пропорциональны?

Напишите здесь ответ с обоснованием: …..

…..

Ну наконец-то, хоть одно обратное утверждение оказалось верным.

Утверждение. Если определитель (2-го порядка) равен нулю, то его столбцы пропорциональны.

Другими словами, если определитель 2-го порядка (со столбцами I и II) равен нулю, то найдется такое число , что II = I.


Как долго мы шли к этому очевидному утверждению!


Ну, теперь-то наверняка дело пойдет значительно быстрее.


З

адача 5.2.а).

Вычислить определитель:


Вычислите!


Вспомните свойство 1.

Верно ли оно для определителей 3-го порядка?


? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какой-либо его столбец равен 0?

Напишите здесь ответ с обоснованием: …..

…..

З

адача 5.2.б).

Вычислить определитель:


В

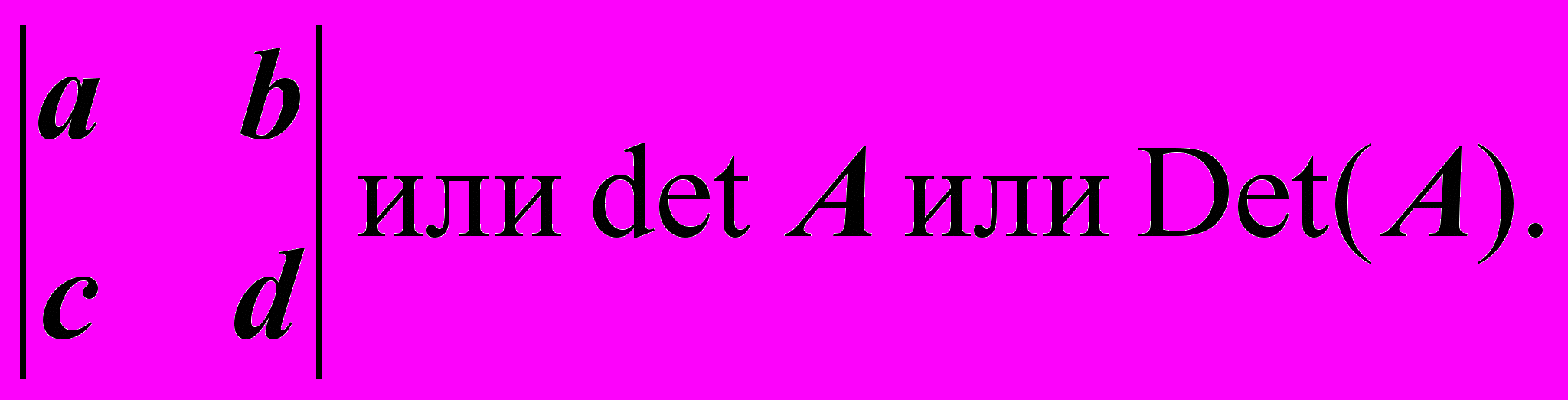
ычислите!


Как видим, определитель (3-го порядка) может быть равен 0, при этом ни один из его столбцов не равен 0.


Вспомните свойство 2.

Верно ли оно для определителей 3-го порядка?


? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какой-либо две его столбца равны друг другу?

Напишите здесь ответ с обоснованием: …..

…..

З

адача 5.2.в).

Вычислить определитель:


Вычислите!


Как видим, определитель (3-го порядка) может быть равен 0, а при этом никакие два его столбца не равны друг другу.


Вспомните свойство 3.

Верно ли оно для определителей 3-го порядка?


? Вопрос: Верно ли обратное утверждение, т.е. если определитель равен 0, то обязательно какие-либо два его столбца пропорциональны?

Напишите здесь ответ с обоснованием: …..

…..

З

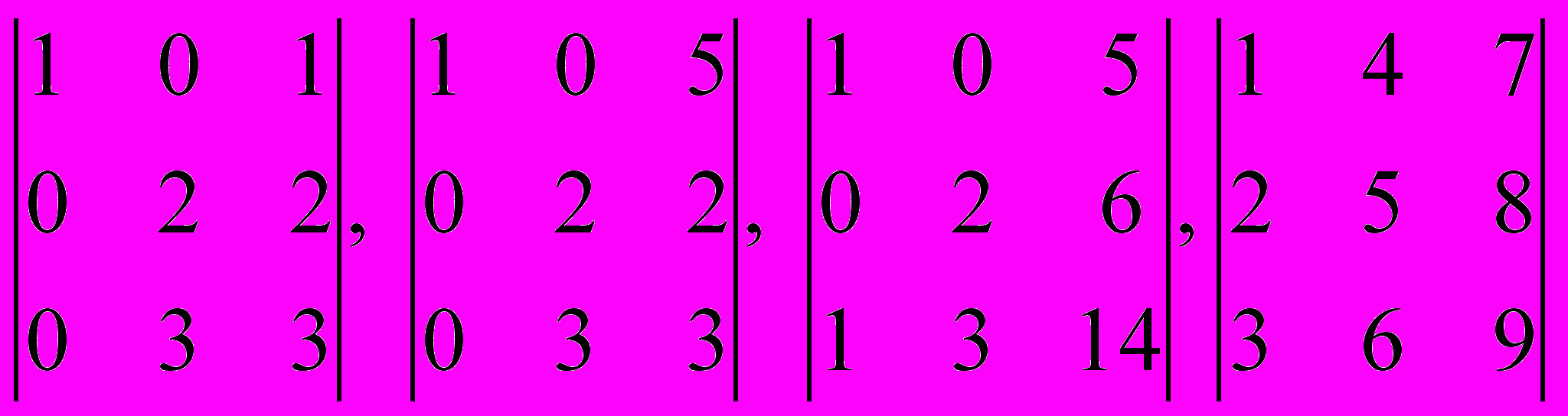
адача 5.2.г).

Вычислить определители:


Вычислите!


Как видим, определитель (3-го порядка) может быть равен 0, а при этом никакие два его столбца не пропорциональны.


? Вопрос: Какое еще свойство определителей (3-го порядка) Вы можете сформулировать?

Напишите это свойство здесь: …..

…..

Свойство 4. Если определитель (3-го порядка) равен 0, то один из его столбцов равен сумме двух других, умноженных на некоторые числа.


Определение. Линейной комбинацией двух столбцов I и II (одинаковых размеров) называется выражение вида I + II.

Итак, определитель (3-го порядка) равен 0, если один из его столбцов равен линейной комбинации двух других его столбцов.


? Вопрос: Верно ли обратное утверждение, т.е. если определитель (3-го порядка) равен 0, то обязательно один из его столбцов равен линейной комбинации двух других его столбцов.

Напишите здесь ответ с обоснованием: …..

…..


К счастью, и это обратное утверждение оказывается верным. В связи с этим введем вспомогательное


Определение. Система столбцов одинакового размера называется линейно зависимой, если один из этих столбцов равен линейной комбинации остальных столбцов.


Задача 5.3.а).

Исследовать на совместность. Если система совместна, решить ее.







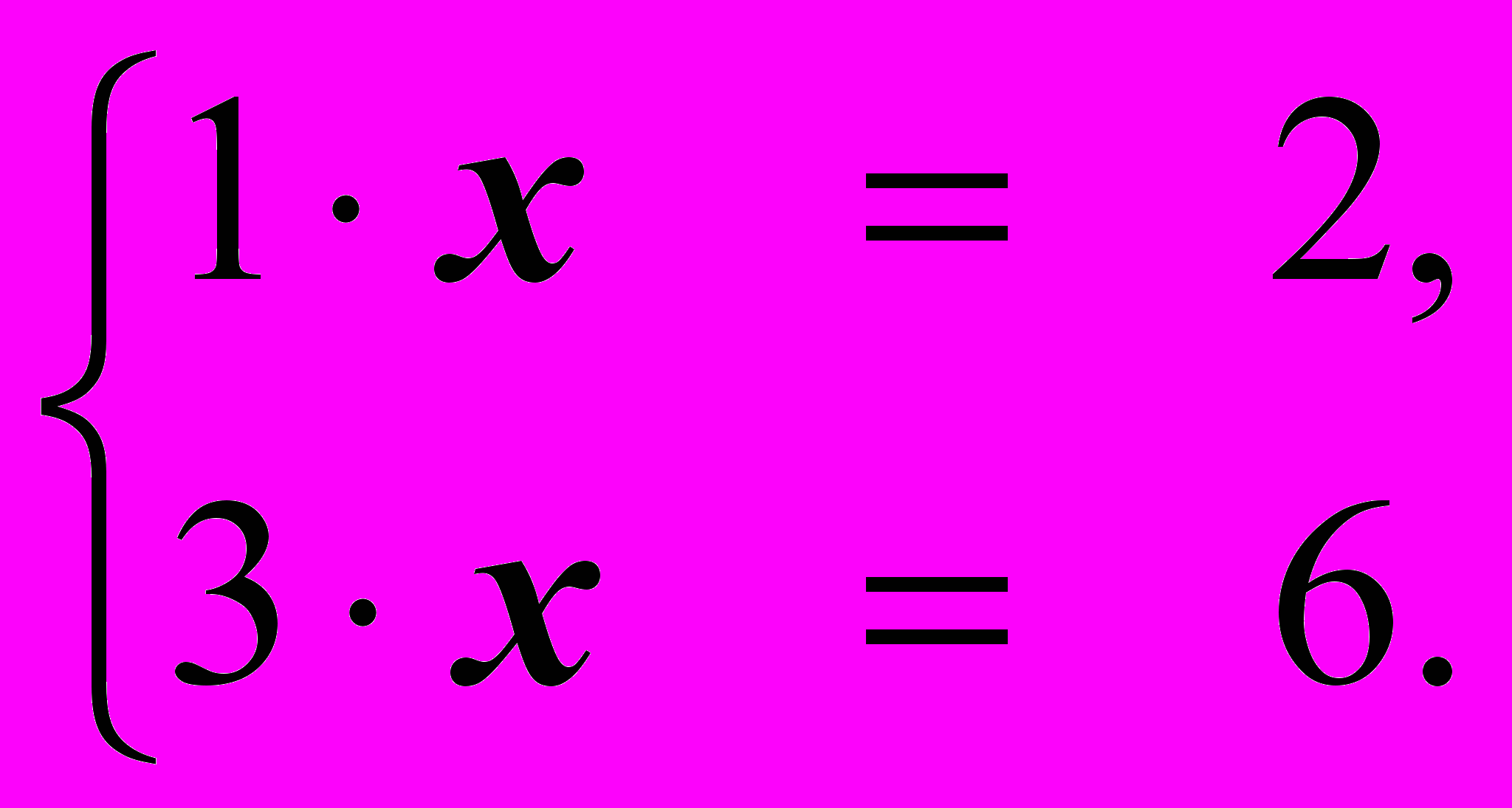
Решение:

Посмотрим на расширенную матрицу системы -


и запишем систему, используя столбцы I и II основной и расширенной матриц:




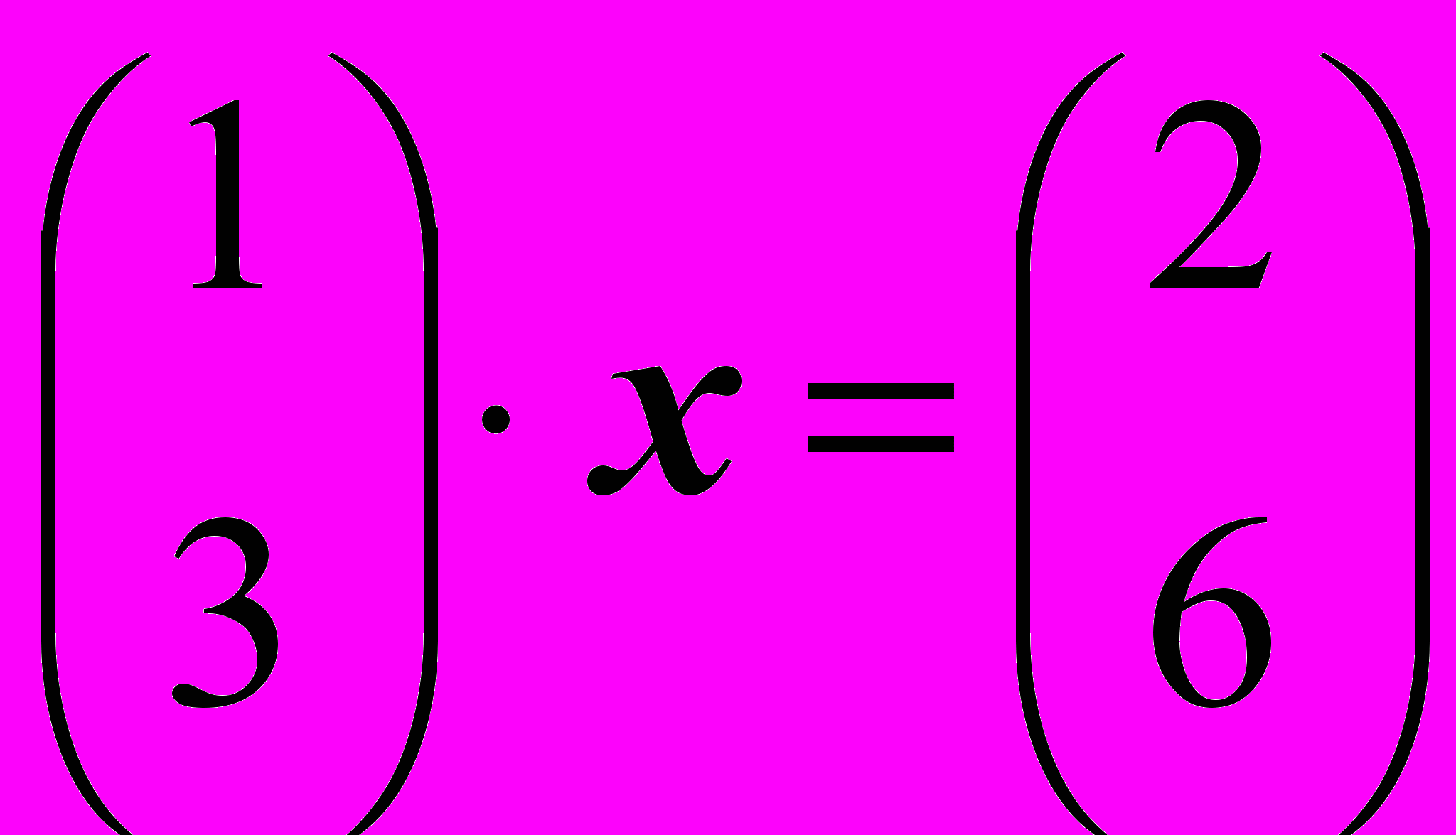
Так как столбцы I и II пропорциональны, то такое уравнение имеет решение.

Этот факт можно сфор­му­лировать "на языке" столбцов:

"Найдется такое число , что выполняется равенство: II = I".

Или то же самое другими словами:

"Столбцы I и II расширенной матрицы линейно зависимы, значит, система с такой расширенной матрицей совместна".

Ответ: система совместна; единственное решение x = 2.


С чем-то подобным мы уже встречались, изучая свойства определителей 2-го порядка, где были два столбца высоты 2. А если система такова, что столбцов в расширенной матрице 2 , а их высота равна не 2, а к примеру, 3?


Задача 5.3.б).

Исследовать на совместность. Если система совместна, решить ее.




Решите самостоятельно!




Решение:

Посмотрим на расширенную матрицу системы -


и запишем систему, используя столбцы I и II основной и расширенной матриц:




Так как столбцы I и II пропорциональны, то такое уравнение имеет решение.

Другими словами, найдется такое число , что выполняется равенство: II = I.

Или "третьими словами", столбцы I и II расширенной матрицы линейно зависимы, значит, система с такой расширенной матрицей совместна".

Ответ: система совместна; единственное решение x = 2.


Задача 5.3.в).

Исследовать на совместность. Если система совместна, решить ее.




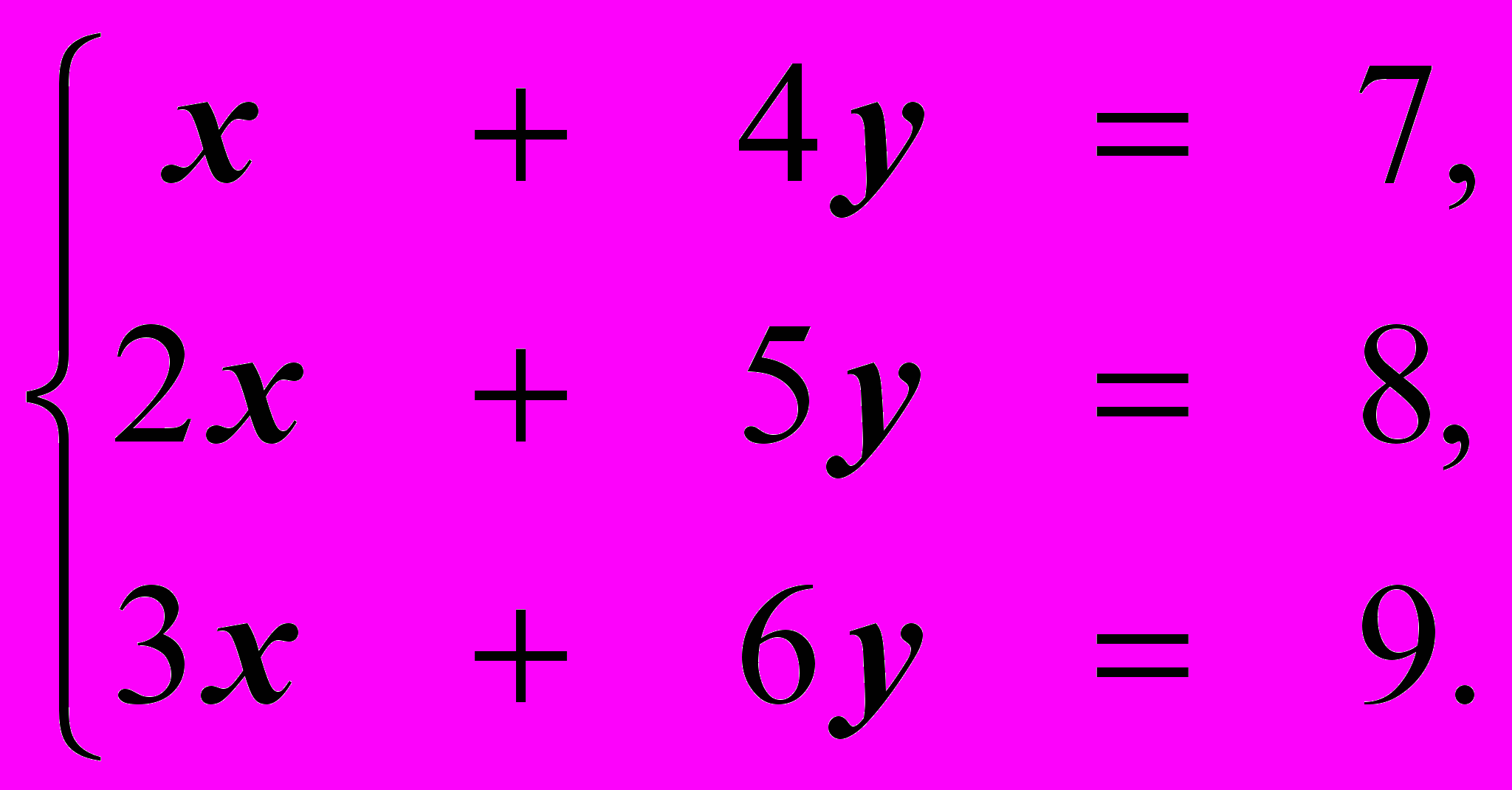
Решите самостоятельно!


Р

ешение:

Предварительно вспомним пример 5.2.г).

Теперь посмотрим на расширенную матрицу системы -


и запишем систему, используя столбцы I, II и III основной и расширенной матриц:




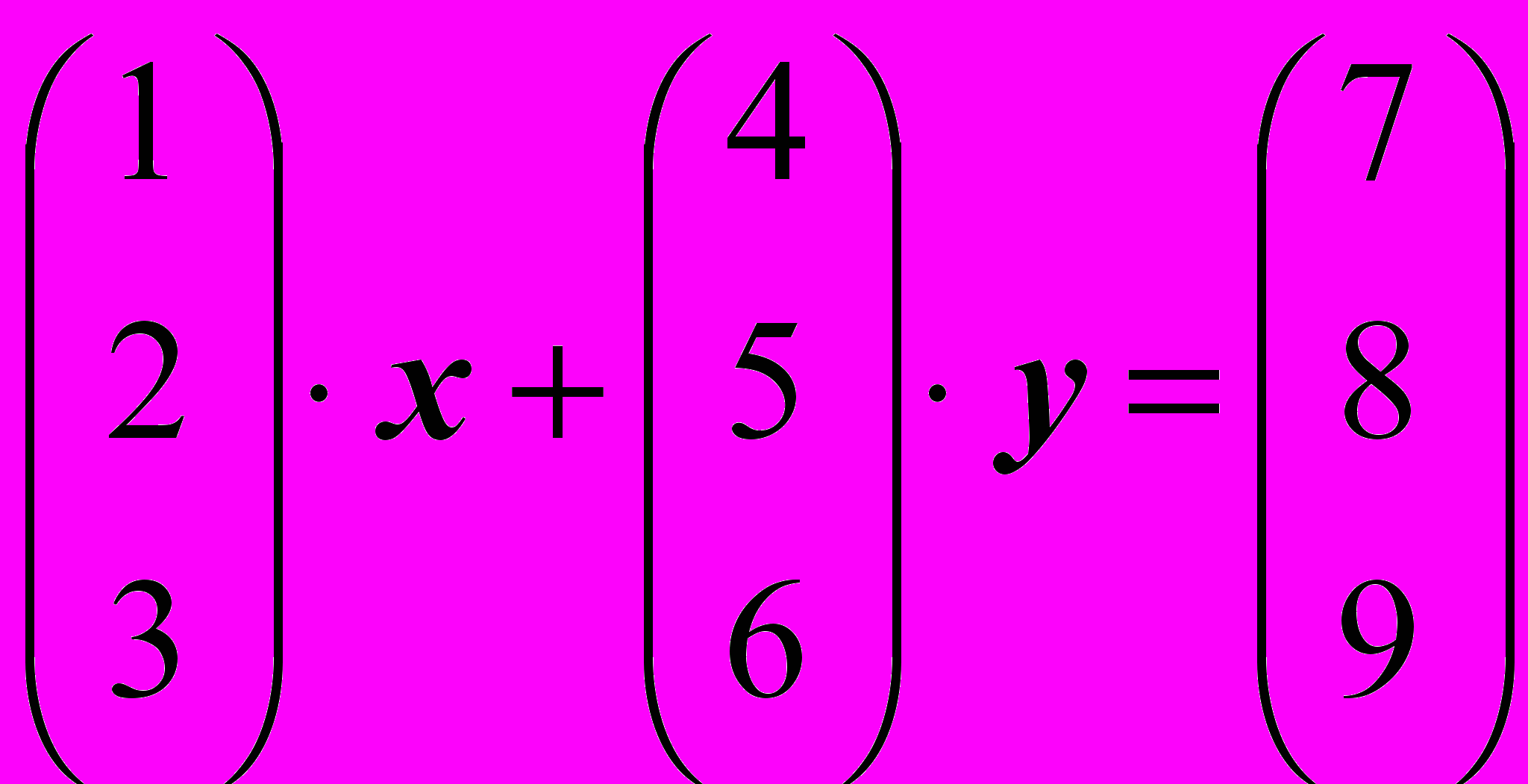
Так как (см. пример 5.2.г.) столбцы I, II и III расширенной матрицы линейно зависимы, то найдутся такие два числа 1 и 2, что выполняется равенство III = 1I + 1II. Значит, система с такой расширенной матрицей совместна.

Ответ: система совместна; единственное решение x = -1, y = 2.


Задача 5.3.г).

Исследовать на совместность. Если система совместна, решить ее.




Решите самостоятельно!

Теперь мы готовы сформулировать теорему - критерий совместности системы линейных алгебраических уравнений.


Сформулируйте самостоятельно!


Т

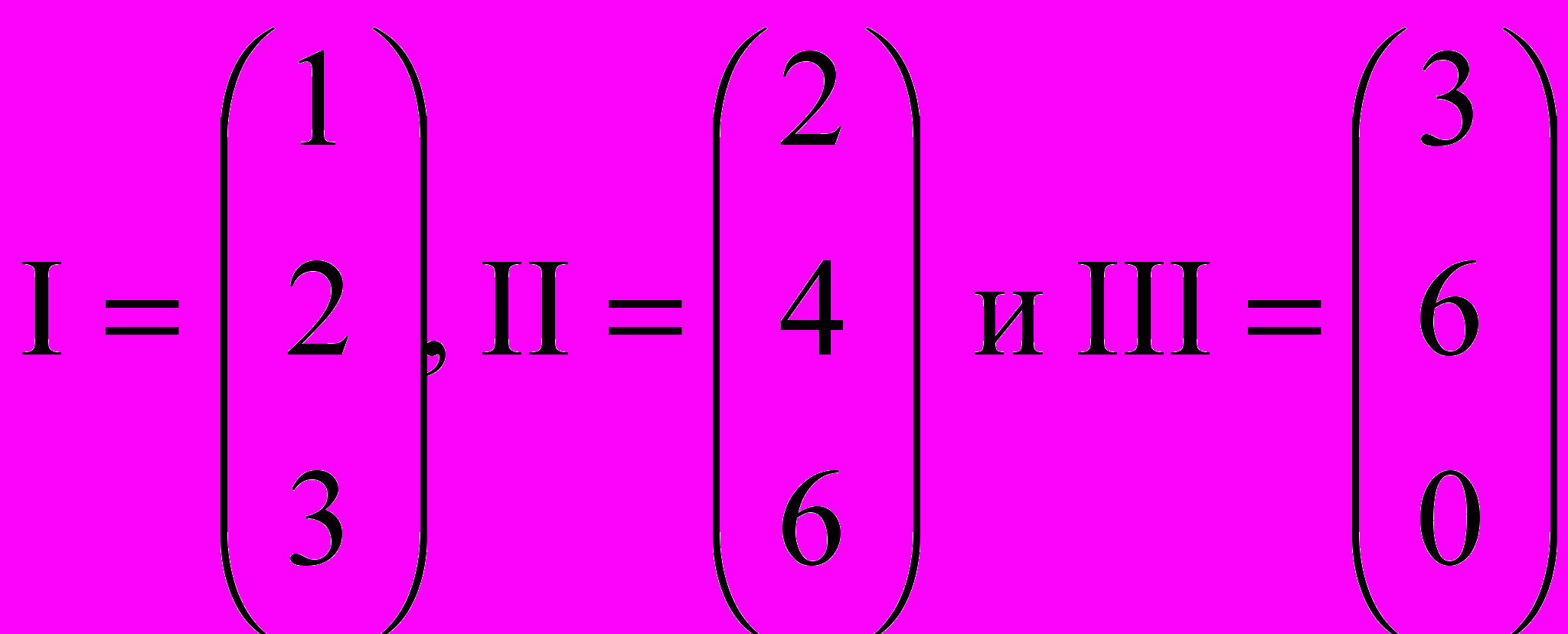
еорема (Кронекера-Капелли) (1). Система линейных алгебраических уравнений совместна тогда и только тогда, когда столбцы расширенной матрицы системы линейно зависимы.

Замечание. Убедитесь, что следующие столбцы

линейно зависимы:

…В самом деле, II = 2I + 0III.

А теперь исследуем на совместность систему:

З

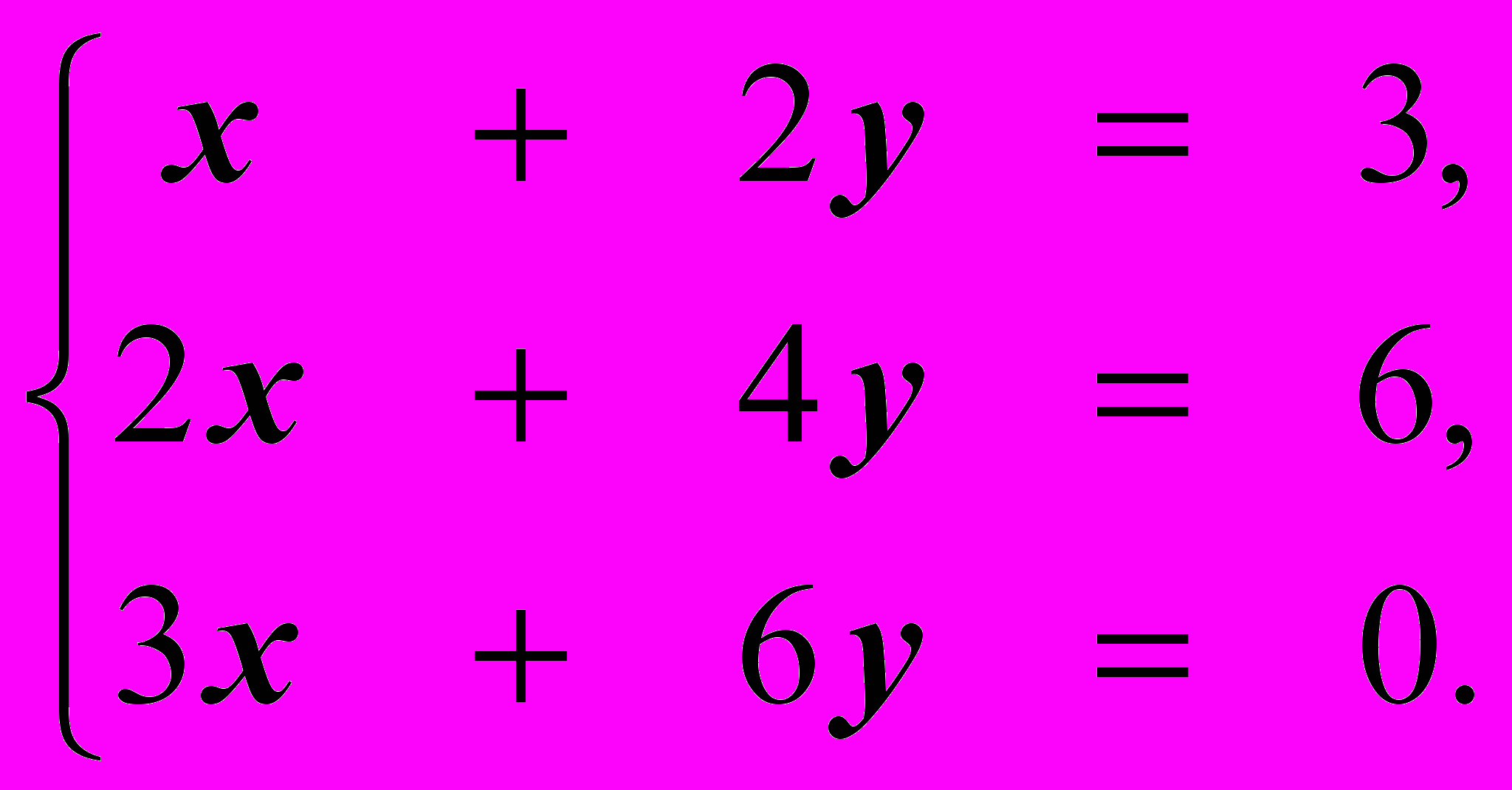
адача 5.3.д).