Лекция № Тема 3: Определители. Формулы Крамера

Вид материала

Лекция

Подобный материал:

• Тематическийпла н, 46.68kb.
• Вопросы к экзамену по курсу «Высшая математика часть, 14.58kb.
• Определители 2-го и 3-го порядков: определения и применение к решению систем линейных, 42kb.
• Лекции по предмету "аналитическая геометрия и линейная алгебра", 82.08kb.
• Тема «Формулы тригонометрии» Лекция, 104.28kb.
• Лекция по векторной алгебре. Лекция по векторной алгебре. Тема, 30.38kb.
• Календарно-тематическое планирование Календарно-тематическое планирование (математика), 232.23kb.
• Лекция №1. Определители, 109kb.
• Стивена Крамера "Creativity Under The Gun", 92.94kb.
• Домашнее задание для 10А на 14-19 февраля, 20.2kb.

Лекция № 4.

Тема 3: Определители. Формулы Крамера.

Нахождение обратной матрицы - метод Гаусса-Жордана.


З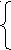адача 4.1а. Решить систему уравнений с помощью обратной матрицы:


ax + by = ,

cx + dy = .


Сначала решите самостоятельно!

Решение:

Запишем систему в виде матричного уравнения:




AX = B, где


В

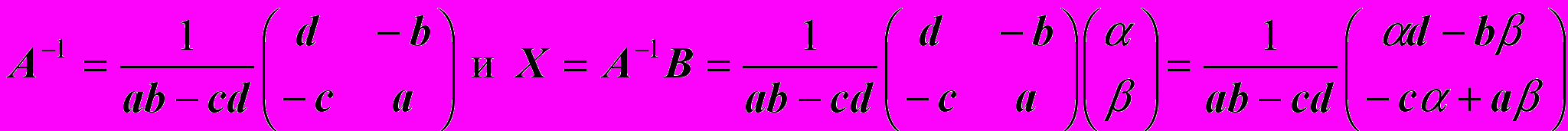
этом случае решение записывается в виде: X = A^-1B, где A^-1 - матрица, обратная к матрице A^-1, значит


откуда получаем


Ответ: Решением системы является упорядоченная пара чисел:





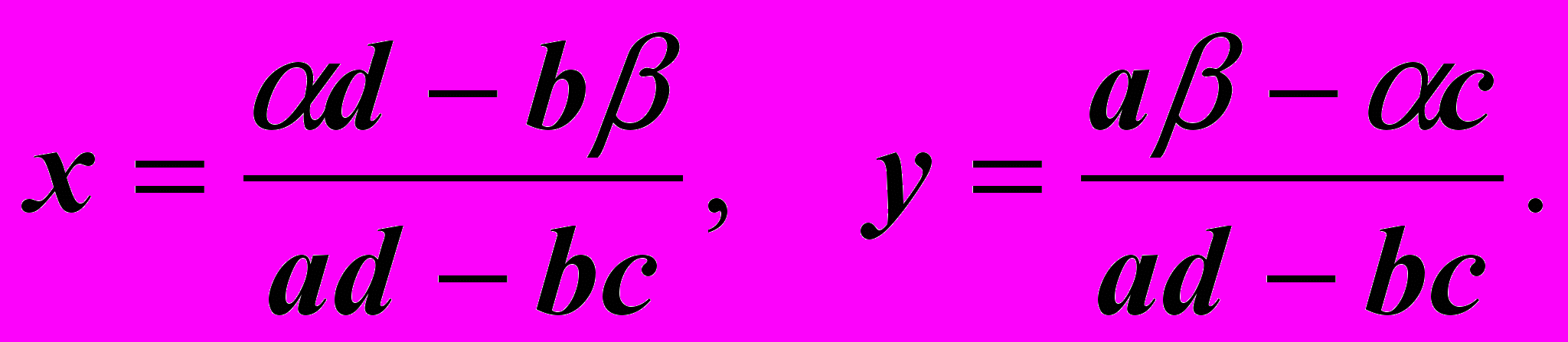
Заметим, что у обеих полученных дробей в знаменателе находится одно и то же выражение ad - bc, очевидно, являющееся некоторой числовой характеристикой основной матрицы исходной системы:







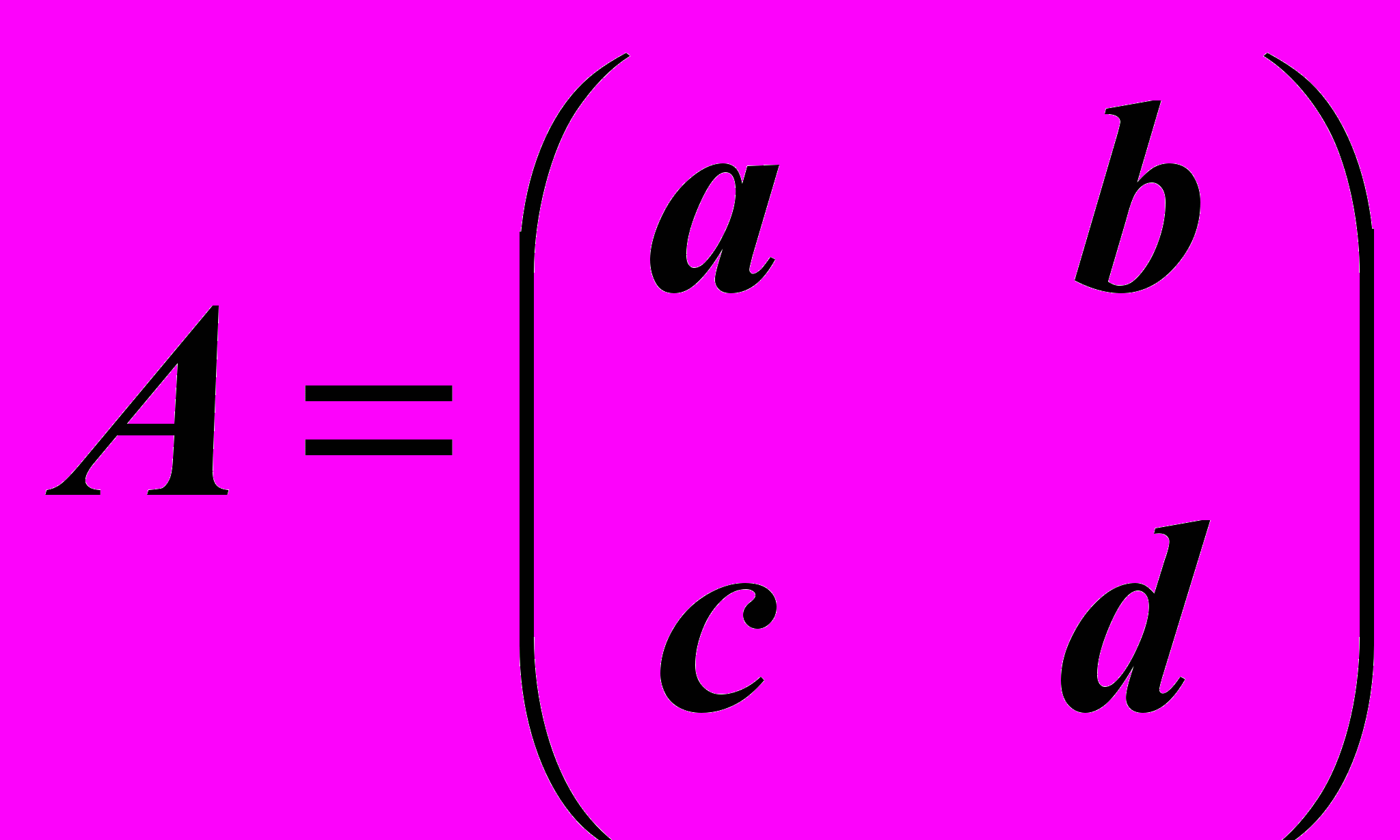
Определение: Выражение ad - bc называется определителем матрицы

и

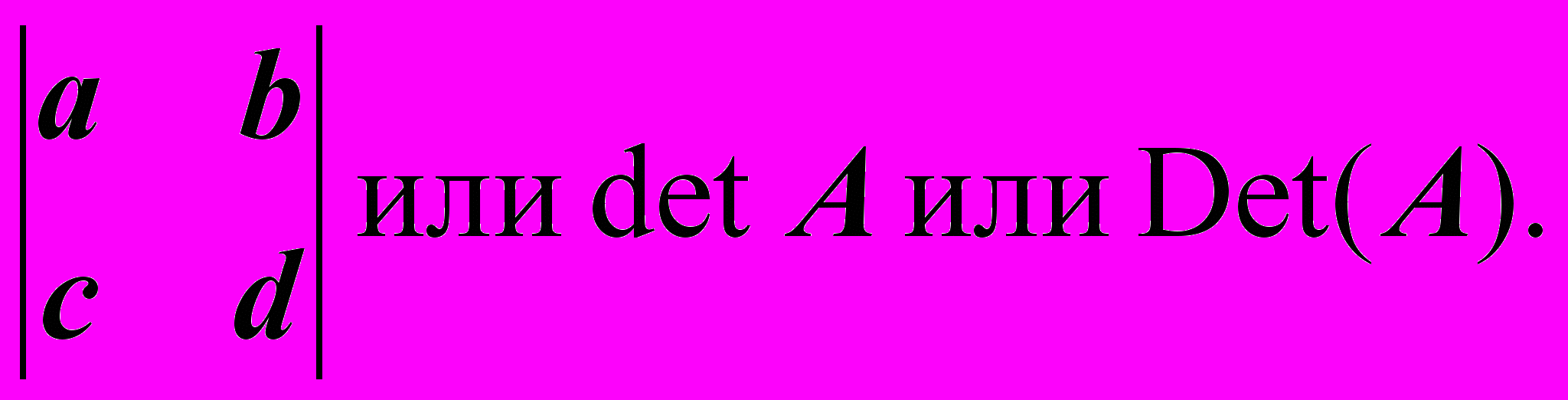
обозначается так:


Значит, знаменатели у обеих полученных дробей равны det A.


А что можно сказать об их числителях ?


Напишите здесь: ………….


……………..


В самом деле, числители обеих дробей также можно записать в виде определителей:






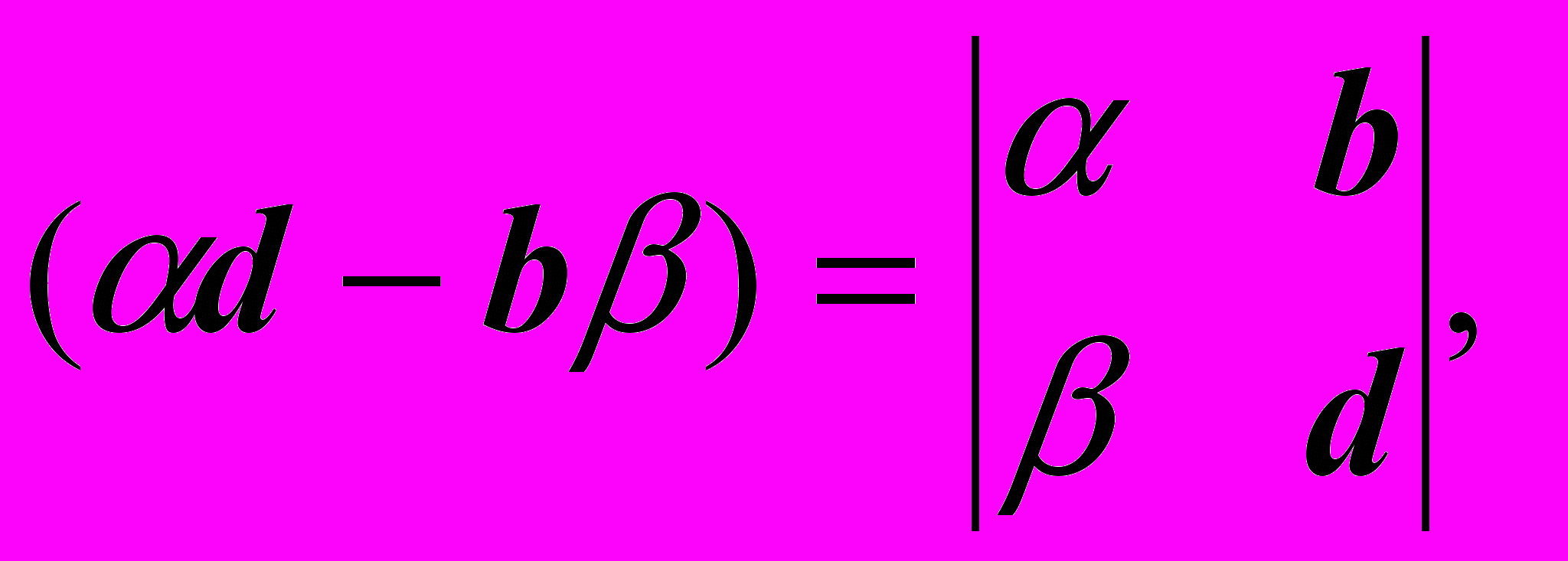
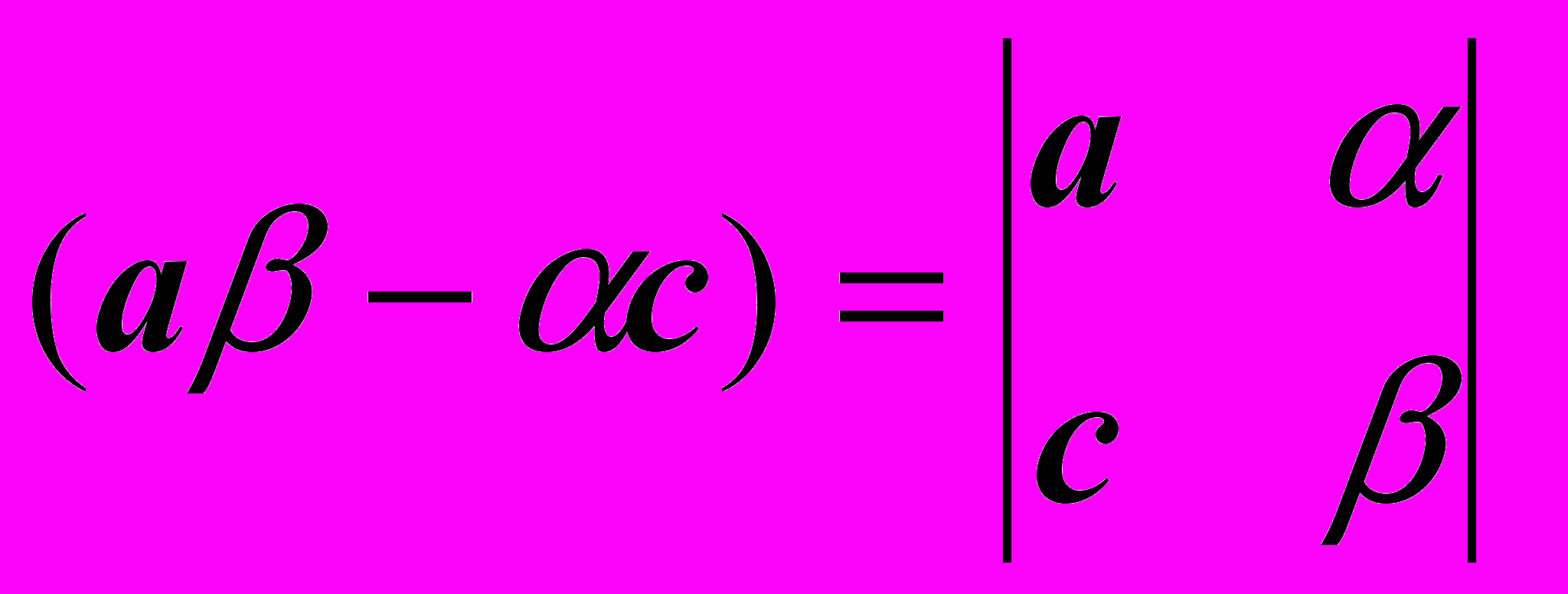
Запишем полученное нами решение, обозначая определители буквами , ₁, ₂:







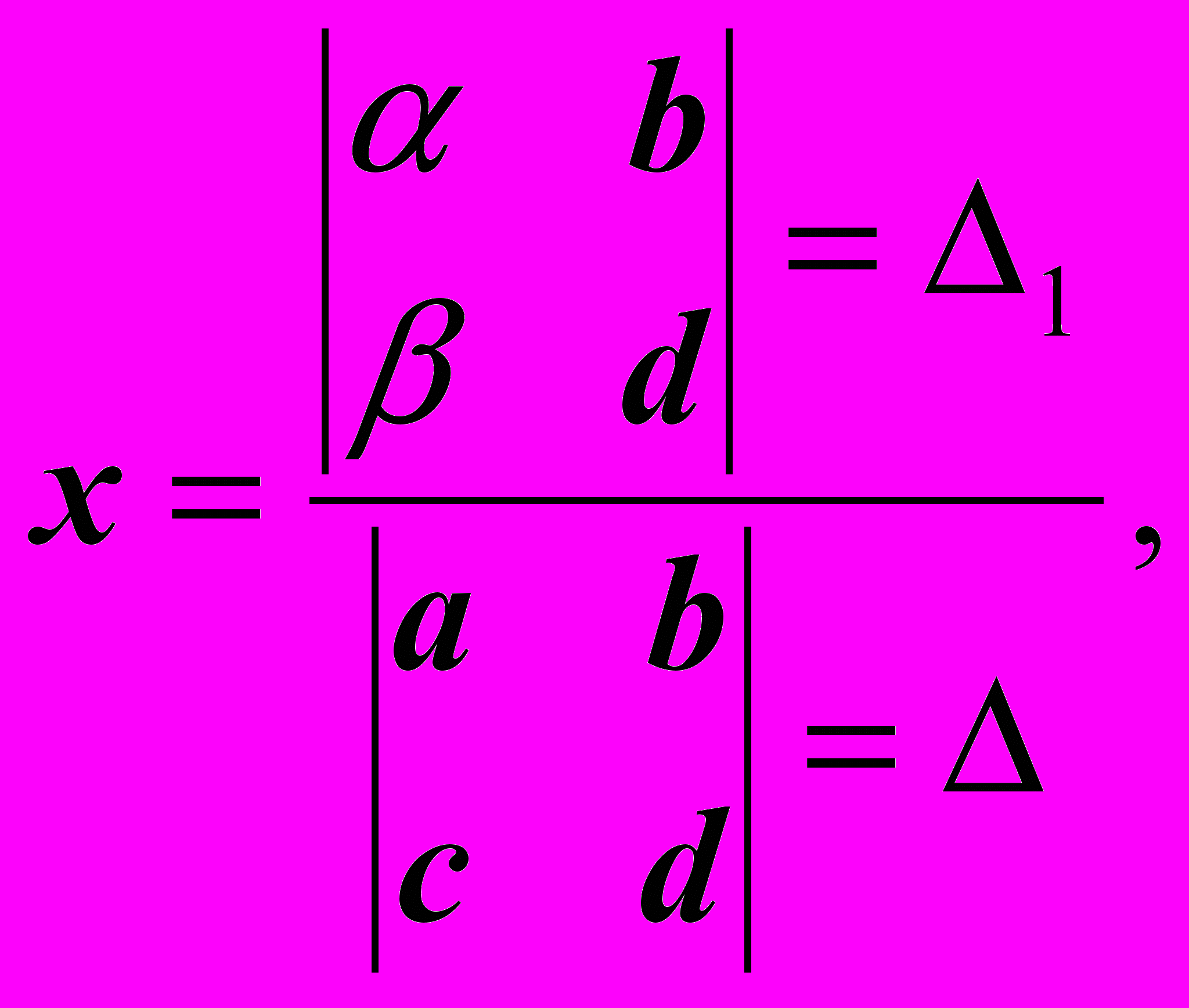
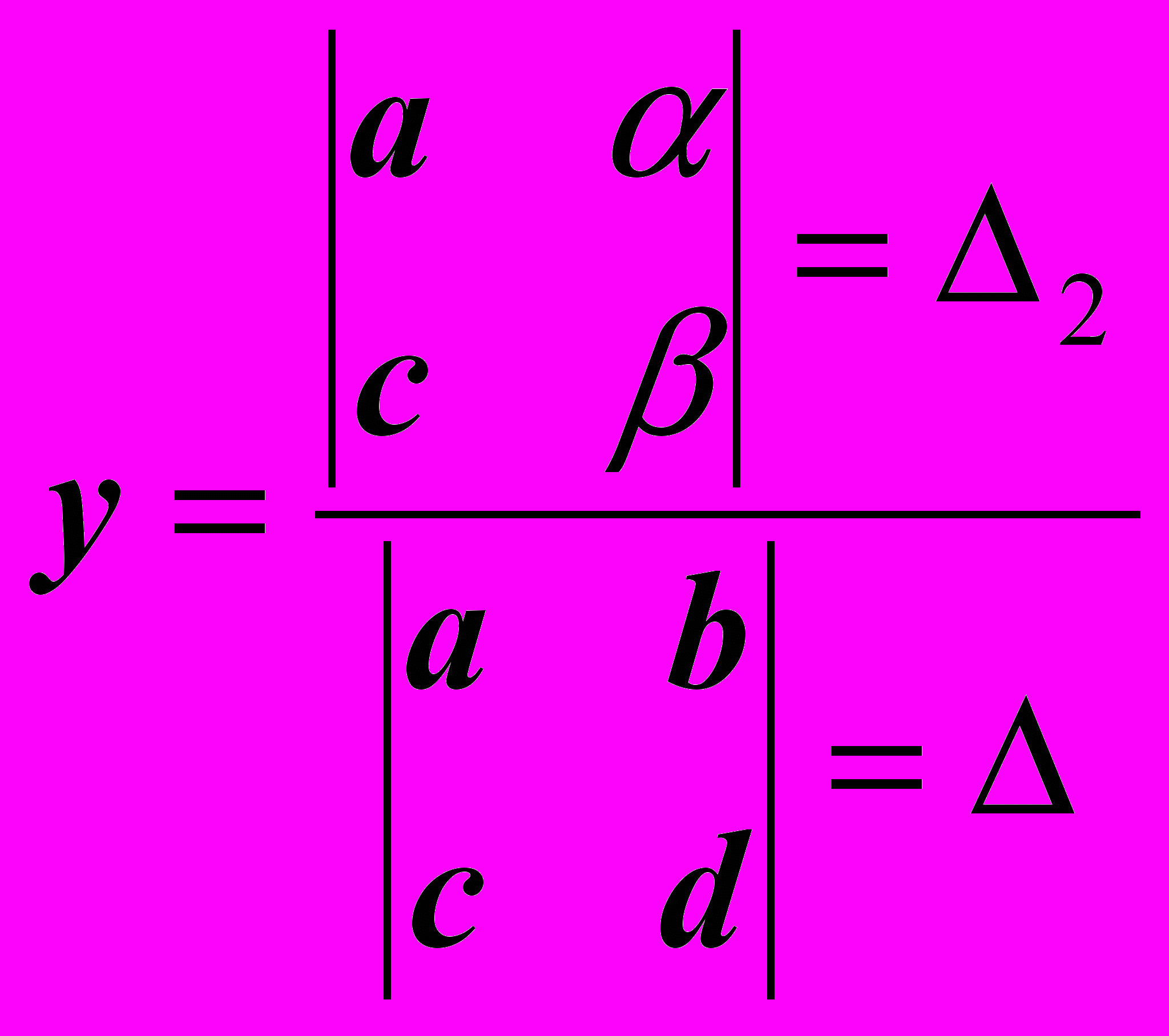
(1)

Как видим, определители ₁ и ₂ получаются из определителя ₁ заменой, соответственно, 1-го и 2- го столбцов на столбец свободных членов.

Формулы (1), представляющие собой запись решения через определители , ₁, ₂, называются формулами Крамера.




Задача 4.2. Решить систему уравнений, используя формулы Крамера:

x + 2y = -3,

x + 3y = -5.

Решение:

Найдем три определителя - , ₁, ₂:




Пользуясь формулами Крамера, запишем решение системы:




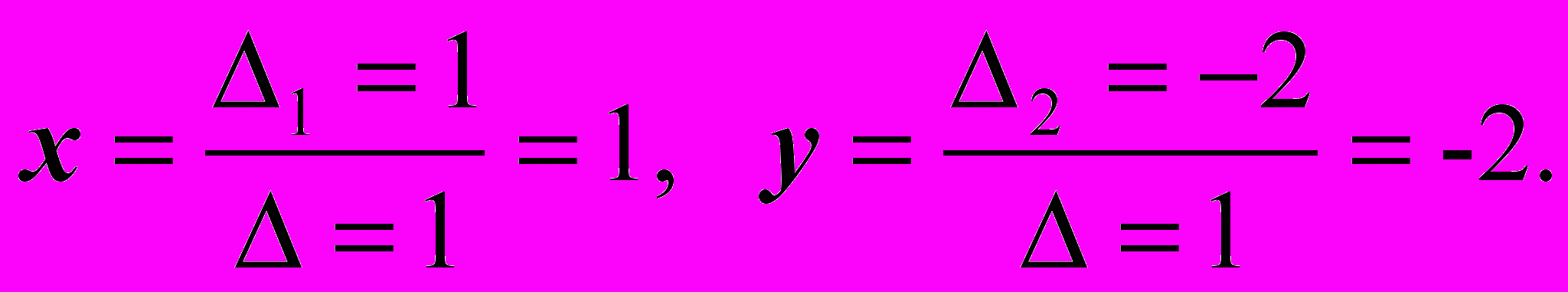
Ответ: x = 1, y = -2.

Обязательно сделайте проверку!


Может возникнуть закономерный вопрос:


"Возможно ли с помощью формул Крамера решать системы бόльших размеров, например, 3х3"?


Оказывается, в случае системы из 3-х уравнений с 3-мя неизвестными x, y и z решение выглядит так:




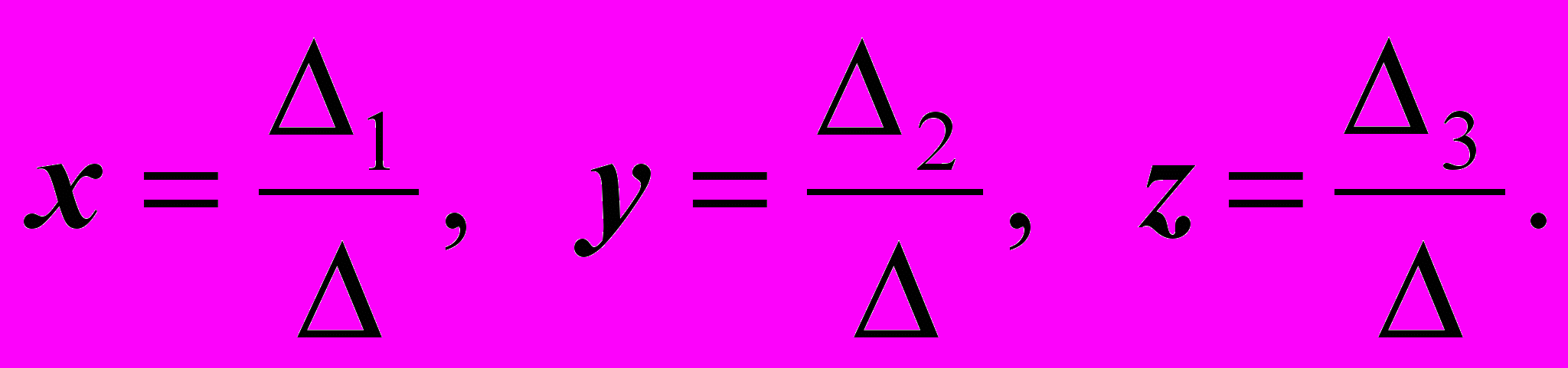
Здесь  - определитель основной матрицы системы, а определители ₁, ₂ и ₃ получаются из  заменой соответственно, 1-го, 2- го и 3-го столбцов на столбец свободных членов.

Остается выяснить, как найти определитель квадратной матрицы 3-го порядка.

Для этого еще раз посмотрим на формулу для определителя матрицы 2-го порядка:




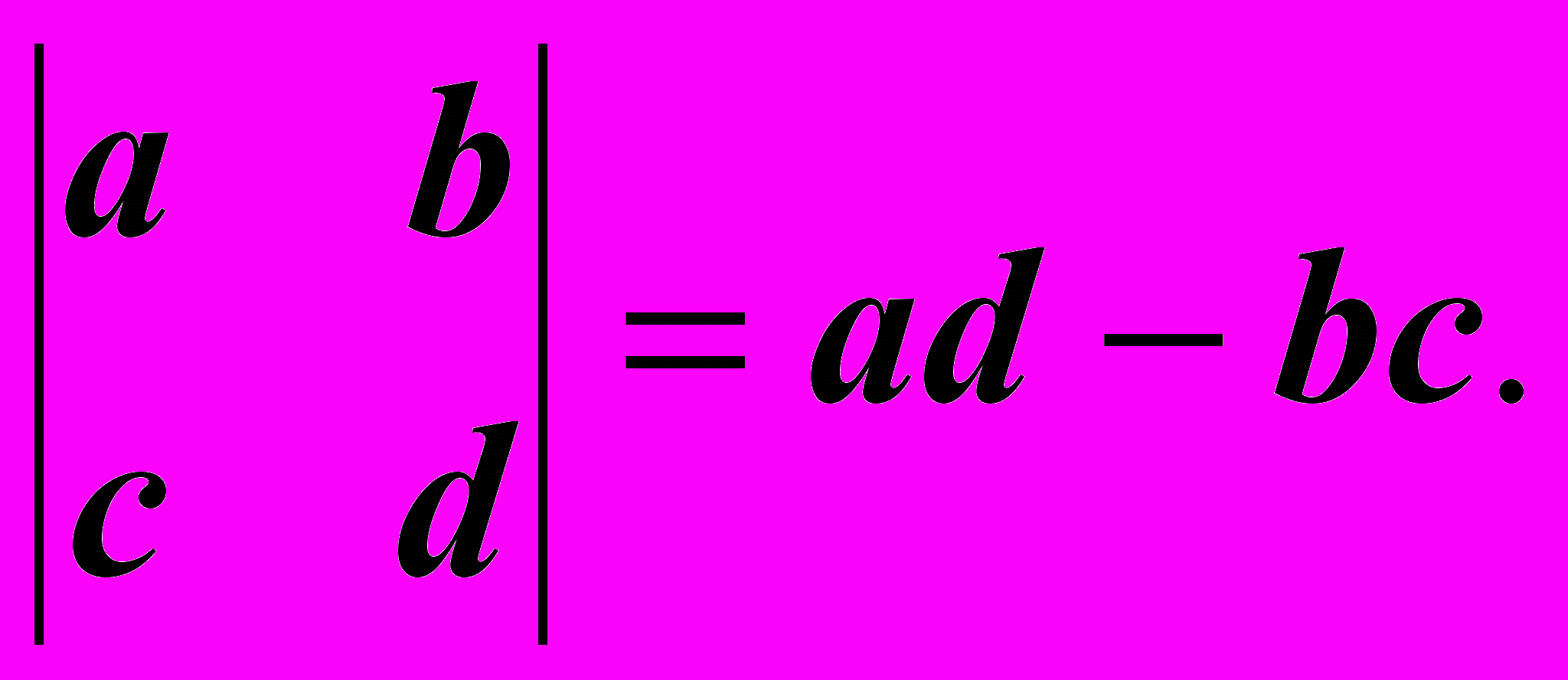
Попробуем прочитать ее следующим образом:

"Будем двигаться по первой строке определителя слева направо. На первом шаге возьмем (со знаком "+") первый элемент этой строки a и умножим его на то, что останется, если вычеркнуть из определителя строку и столбец, содержащие a:









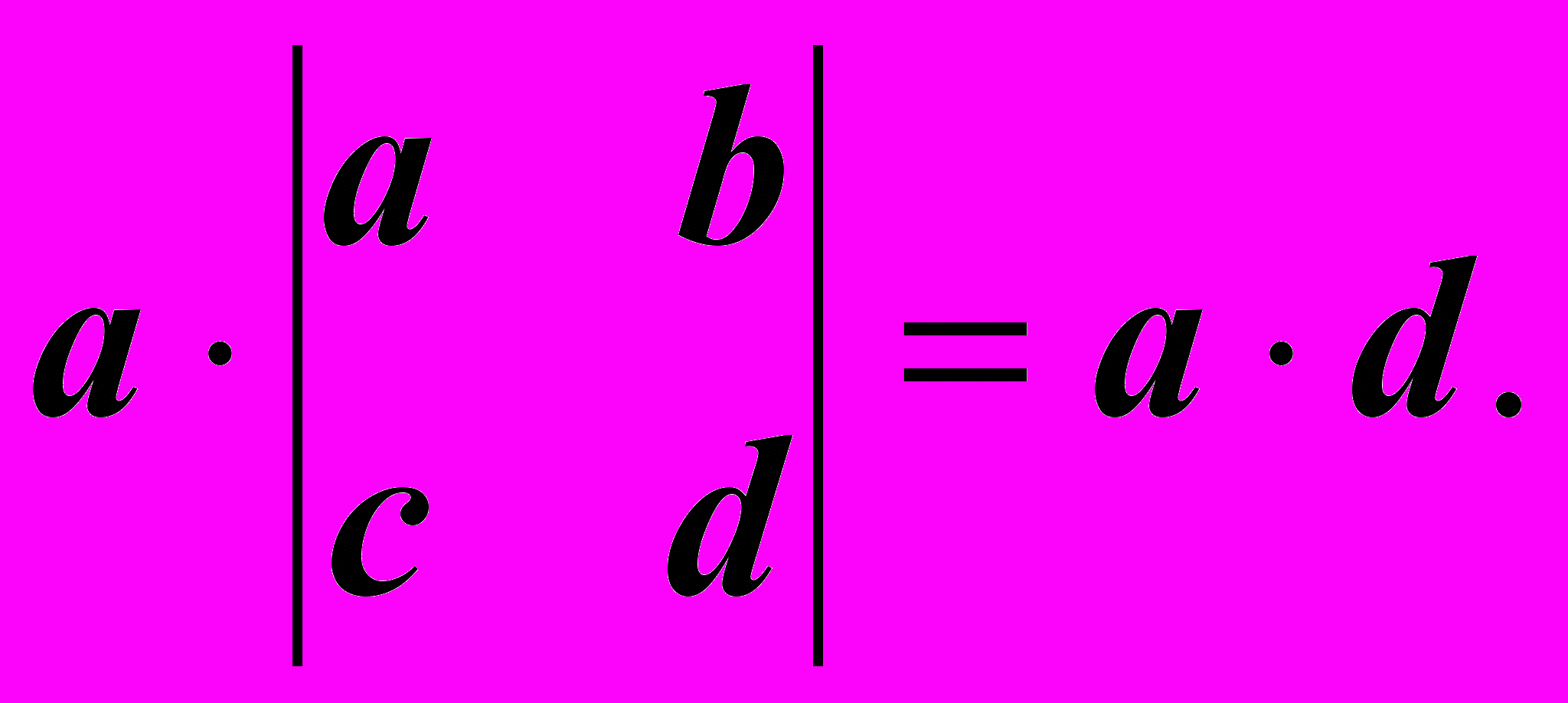
На втором шаге возьмем (со знаком "-") следующий элемент первой строки b и умножим его на то, что останется, если вычеркнуть из определителя строку и столбец, содержащие b:









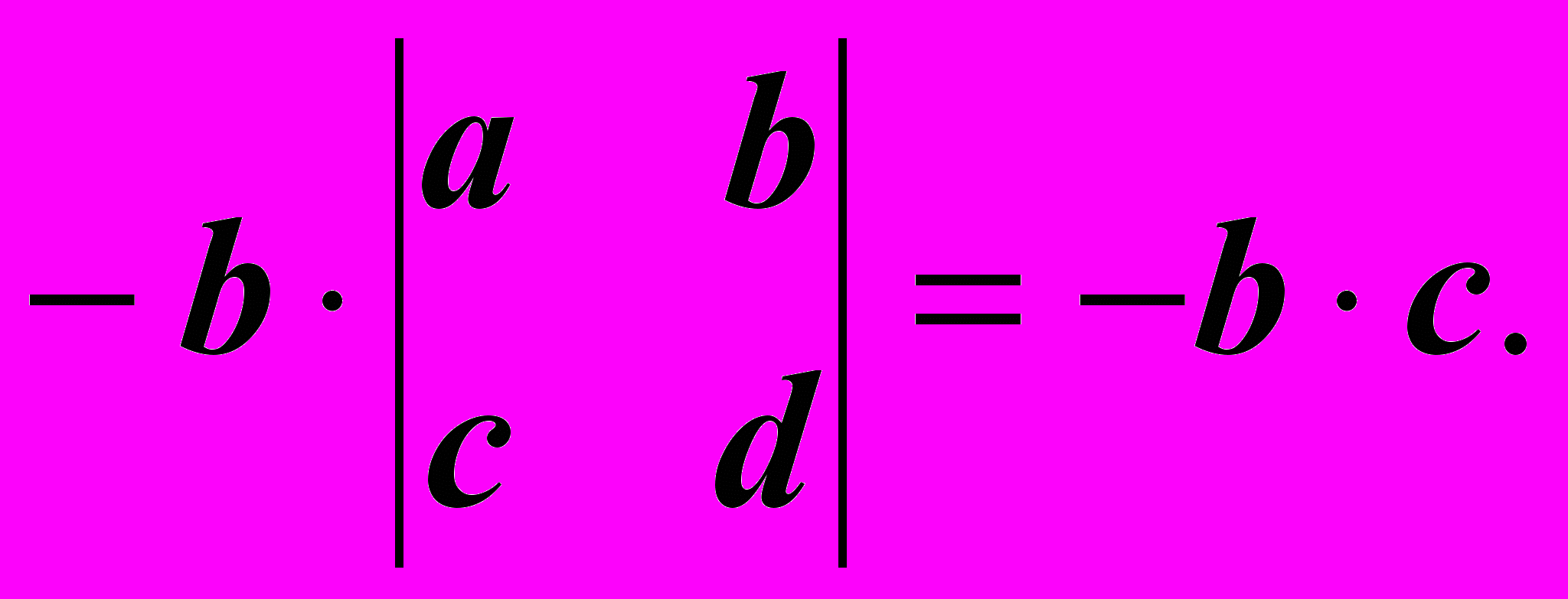
Сложив (два) полученные произведения (одно - со знаком "+" и одно - со знаком "-"): ad - bc, получим исходный определитель ad - bc".


Попробуем теперь применить подобный алгоритм к вычислению определителя квадратной матрицы A, но теперь уже 3-го порядка:




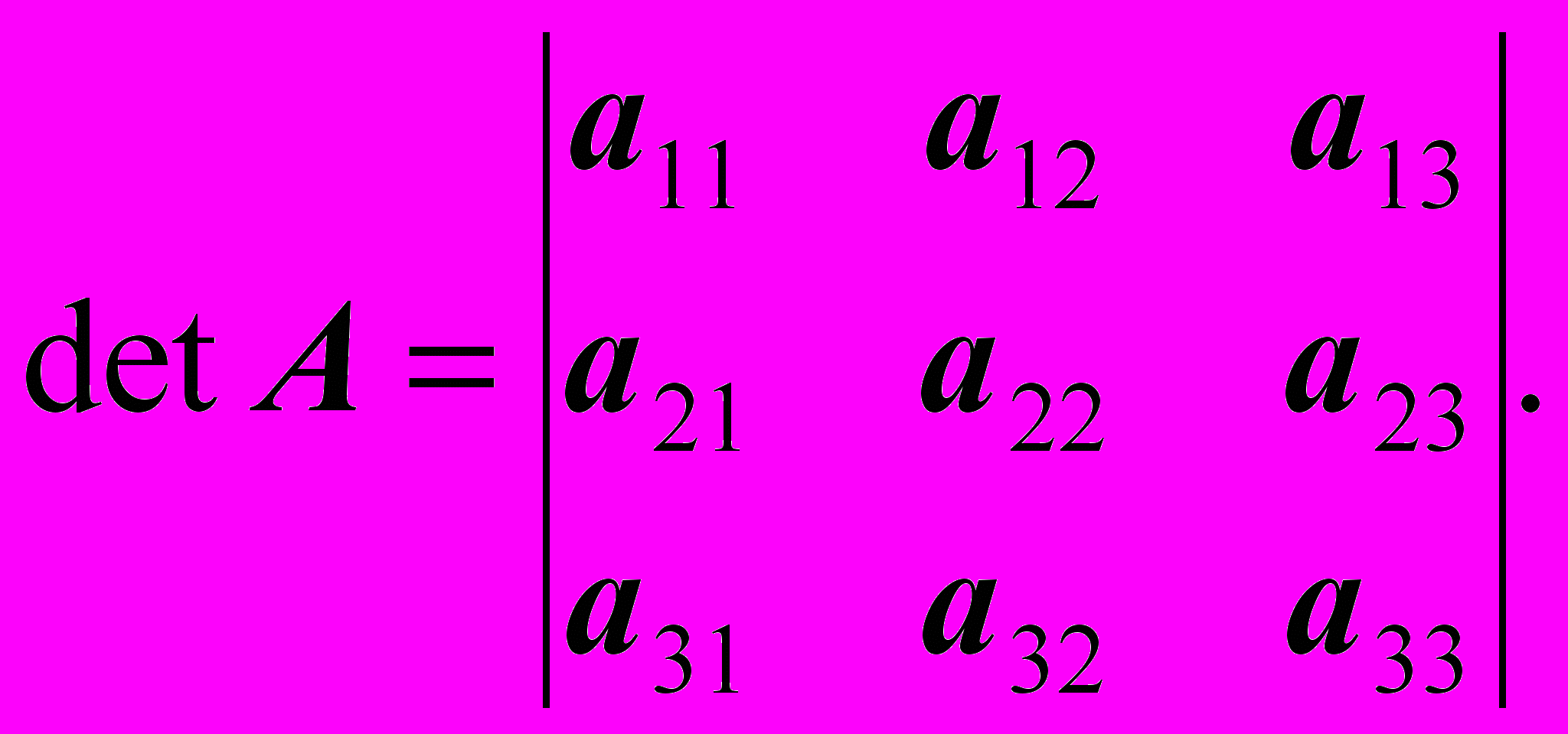
"Будем двигаться по первой строке определителя слева направо. На первом шаге возьмем (со знаком "+") первый элемент этой строки a₁₁ и умножим его на то, что останется, если вычеркнуть из определителя строку и столбец, содержащие a₁₁:







На втором шаге возьмем (со знаком "-") следующий элемент первой строки a₁₂ и умножим его на то, что останется, если вычеркнуть из определителя строку и столбец, содержащие a₁₂:








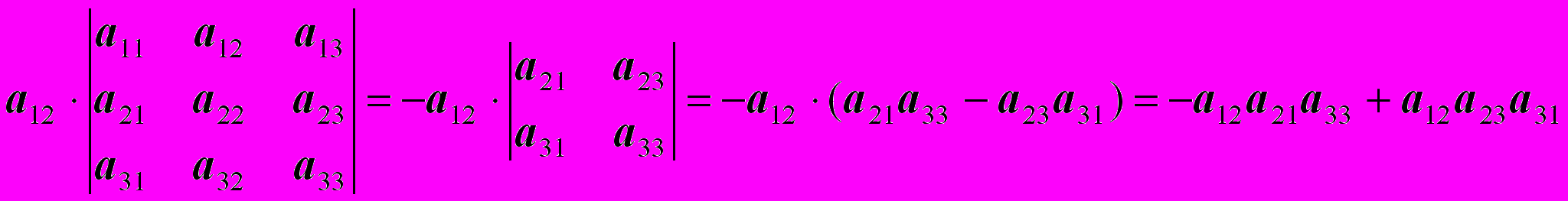
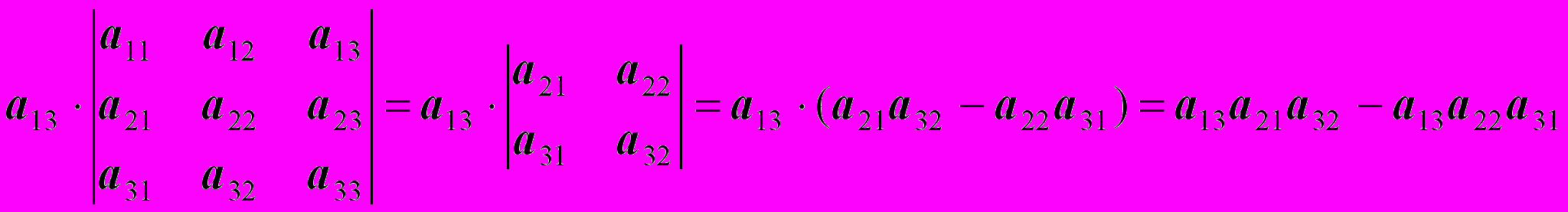
На третьем шаге возьмем (уже опять со знаком "+") следующий элемент первой строки a₁₃ и умножим его на то, что останется, если вычеркнуть из определителя строку и столбец, содержащие a₁₃: