Geum.ru

Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материалаРабочая учебная программа

Содержание


§4. Элементы теории корреляции. Линейная корреляция
Подобный материал:
1   ...   28   29   30   31   32   33   34   35   36

§4. Элементы теории корреляции. Линейная корреляция


Корреляционной зависимостью называется статистическая зависимость, при которой изменение одной из величин влечет за собой изменение среднего значения другой:

, (1)

где - условная средняя (среднее арифметическое значений ,соответствующих значению ).

Уравнение (1) называется уравнением регрессии на , функция называется регрессией на , а ее график – линия регрессии на .

Аналогично определяется регрессия на .

Если обе линии регрессии Y на Х и Х на Y – прямые, то корреляцию называют линейной.

Выборочное уравнение прямой линии регрессии Y на Х имеет вид

(2)

где - условная средняя; и - выборочные средние признаков Х и Y; и - выборочные средние квадратичные отклонения; - выборочный коэффициент корреляции, причем

(3)

Выборочное уравнение прямой линии регрессии Х на Y имеет вид

(4)

Если данные наблюдений над признаками Х и Y заданы в виде корреляционной таблицы с равностоящими вариантами, то целесообразно перейти к условным вариантам:

(5)

где С1 – «ложный нуль» вариант Х (новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту); h1 – шаг, т.е. разность между двумя соседними вариантами Х; С2 – ложный нуль вариант Y; h2 – шаг вариант Y.

В этом случае выборочный коэффициент корреляции

(6)

причем слагаемое удобно вычислять, используя расчетную таблицу 3 (см. далее решение задачи).

Величины могут быть найдены либо методом произведений (при большом числе данных), либо непосредственно по формулам:

(7)

Зная эти величины, можно определить входящие в уравнения регрессии (2) и (4) величины по формулам:



Для оценки силы линейной корреляционной связи служит выборочный коэффициент корреляции .

Для обоснованного суждения о наличии связи между количественными признаками следует проверить, значим ли выборочный коэффициент корреляции.

Пример 2. Данные наблюдений над двумерной случайной величиной (X,Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на Х. Выполнить чертеж.

Таблица 1.

Y
X
ny

20
25
30
35
40

16

26

36

46

56
4
6

8

10

32

4


3

12

1


9

6

5
10

18

44

22

6

nx
4
14
46
16
20
N=200


Решение.

Составим корреляционную таб. 2 в условных вариантах, выбрав в качестве ложных нулей С1=30 и С2=36 (каждая из этих вариант расположена в середине соответствующего вариационного ряда).

Таблица 2.

v
u

-2
-1
0
1
2
nv

-2
4
6









10

-1



8
10






18

0






32
3
9
44

1






4
12
6
22

2









1
5
6

nu
4
14
46
16
20
N=100

Найдем и :



Найдем вспомогательные величины и :



Найдем и



Найдем , для чего составим расчетную таблицу 3.
  1. Произведение частоты nuv на варианту u, т. е. nuvu, запишем в правом верхнем углу клетки, содержащей значение частоты. Например, в правых верхних углах клеток первой строки запишем произведения:
  2. Суммируем все числа, помещенные в правых верхних углах клеток одной строки, и их сумму помещаем в клетку этой же строки «столбца U». Так, для первой строки .
  3. Умножим варианту v на U и полученное произведение запишем в соответствующую клетку «столбца vU». Так, в первой строке таблицы , следовательно, .
  4. Сложив все числа «столбца vU», получим сумму , которая равна искомой сумме . Так, для таблицы 3 , следовательно,

Суммируя числа последнего столбца таблицы 3, находим

Для контроля вычислений находим сумму чисел последней строки:



Совпадение сумм свидетельствует о правильности вычислений.

Для контроля аналогичные вычисления производят по столбцам: произведения записывают в левый нижний угол клетки, содержащей значение частоты; все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму помещают в «строку V»;наконец, умножают каждую варианту u на V и результат записывают в клетках последней строки.

Таблица 3.

u

v
-2
-1
0
1
2
U=
vU

-2
-8

4

-8
-6

6

-12









-14
28

-1



-8

8

-8
0

10

-10






-8
8

0






0

32

0
3

3

0
18

9

0
21
0

1






0

4

4
12

12

12
12

6

6
24
24

2









1

1

2
10

5

10
11
22

V=
-8
-20
-6
14
16





uV
16
20
0
14
32





Найдем искомый выборочный коэффициент корреляции:



Найдем шаги и (разности между любыми двумя соседними вариантами):



Найдем и , учитывая, что



Найдем и :



Подставим найденные величины в соотношение (1), получим искомое уравнение прямой линии регрессии Y на X:



или окончательно .

Построим график:



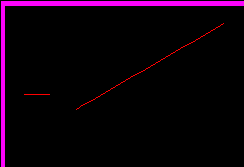
Ответ: .