Geum.ru

Рабочая программа по дисциплине: математический анализ направление

Вид материалаРабочая программа

Содержание


Студент должен знать
Студент должен уметь
Студент должен иметь навыки
реферирования научной литературы по указанной тематике.
2.2. Темы и их содержание
4. Непрерывность функции.
6. Основные теоремы дифференциального исчисления и их приложения.
8. Определённый интеграл.
9. Приложения определённого интеграла.
10. Несобственные интегралы.
12. Функциональные ряды.
15. Нормированные пространства.
17. Дифференцирование функции нескольких переменных.
18. Геометрический смысл функции нескольких переменных.
19. Экстремум функции нескольких переменных.
21. Применение кратных интегралов.
22. Криволинейные интегралы.
24. Дифференциальные уравнения первого порядка.
25. Дифференциальные уравнения высших порядков.
26. Системы дифференциальных уравнений.
...
Полное содержание
Подобный материал:
1   2   3

Студент должен знать:

  • основные понятия (предела последовательности; предела функции одной и нескольких переменных; точной верхней и точной нижней граней; непрерывности; равномерной непрерывности; производной и дифференциала; экстремума и локального экстремума функции; неопределённого, определённого, несобственного, кратного, криволинейного интегралов; суммы числового и функционального рядов; неявной и параметрически заданной функции, метрического и гильбертова пространств; дифференциального уравнения; системы дифференциальных уравнений),

  • формулировки важнейших теорем (о пределе числовой последовательности; о непрерывных и дифференцируемых функциях одного и нескольких переменных; о неопределённом, определённом, кратном и криволинейном интегралах; о числовых и функциональных рядах; о сжимающих отображениях в банаховых пространствах; об общем и частном решениях дифференциального уравнения и т.д.).


Студент должен уметь:

  • находить предел числовой последовательности и функции;
  • вычислять производную и интеграл;
  • строить и исследовать графики функций одного и нескольких переменных;
  • исследовать на сходимость (в том числе, равномерную) числовые и функциональные ряды;
  • раскладывать функцию в ряд Тейлора и ряд Фурье;
  • приводить примеры метрических, нормированных и гильбертовых пространств;
  • решать дифференциальные уравнения различных типов и их системы.


Понятия: базисными понятиями курса являются понятия: функции, последовательности, предела, непрерывности, производной, дифференциала, интеграла, ряда, пространства, дифференциального уравнения.

Студент должен иметь навыки:

  • интерпретации конструкций, создаваемых математическим анализом, внутри математики и за её пределами – в приложениях, решении проблемных и прикладных задач;

  • реферирования научной литературы по указанной тематике.



II. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ


2.1. Основные разделы дисциплины
  1. Введение в математический анализ.
  2. Дифференциальное исчисление функций одной переменной.
  3. Интегральное исчисление функций одной переменной.
  4. Ряды.
  5. Элементы функционального анализа.
  6. Дифференциальное исчисление функций нескольких переменных.
  7. Интегральное исчисление функций нескольких переменных.
  8. Дифференциальные уравнения и их системы.


2.2. Темы и их содержание

Тема 1. Введение в математический анализ.

1. Множества. Действительные числа.

Множество R действительных чисел. Изображение действительных чисел на прямой. Модуль действительного числа. Ограниченные и неограниченные множества. Числовые промежутки.

2. Функции.

Функции и их общие свойства. График функции. Способы задания функций. Обратная функция. Сложная функция. Действительная функция действительной переменной. Основные элементарные функции и их графики. Числовые последовательности. Подпоследовательности.

3. Предел.

Понятие предела последовательности и предела функции. Предел отношения синуса к аргументу, стремящемуся к нулю. Единственность предела. Предел суммы, произведения и частного. Предел сложной функции. Предельный переход в неравенствах. Односторонние пределы. Бесконечно малые функции и их сравнение. Связь между функцией, её пределом и бесконечно малой. Сравнение бесконечно малых функций. Бесконечно большие функции.

Непрерывность множества R. Верхняя и нижняя грани числового множества. Предел монотонной последовательности. Число е и связанные с ним пределы. Теорема Больцано-Вейерштрасса.

4. Непрерывность функции.

Непрерывность функции в точке. Непрерывность функции в интервале и на отрезке. Непрерывность суммы, произведения и частного. Переход к пределу под знаком непрерывной функции. Односторонняя непрерывность. Точки разрыва функции и их классификация. Теорема о промежуточных значениях непрерывной функции. Непрерывность обратной функции.

Тема 2. Дифференциальное исчисление функций одной переменной.

5. Производная и дифференциал.

Дифференцируемость функции. Производная и дифференциал, их геометрический и механический смысл. Непрерывность дифференцируемой функции. Дифференцирование суммы, произведения и частного. Производная и дифференциал сложной функции. Производная обратной функции. Производные основных элементарных функций. Производные и дифференциалы высших порядков. Механический смысл второй производной. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Гиперболические функции. Касательная и нормаль к кривой.

6. Основные теоремы дифференциального исчисления и их приложения.

Теоремы Ролля, Лагранжа, Коши. Правила Лопиталя. Признаки постоянства, возрастания и убывания функции в точке и на промежутке. Максимум и минимум функции. Нахождение наибольших и наименьших значений функции на отрезке. Выпуклость графика функции. Точки перегиба. Асимптоты. Применение дифференциального исчисления к построению графиков функций.

Тема 3. Интегральное исчисление функций одной переменной.

7. Неопределённый интеграл.

Первообразная функция и неопределённый интеграл. Основные свойства неопределённого интеграла. Таблица основных неопределённых интегралов. Непосредственное интегрирование. Метод интегрирования подстановкой (заменой переменой). Интегрирование по частям. Интегрирование рациональных функций. Интегрирование тригонометрических функций. Интегрирование иррациональных функций. Интегралы, «не берущиеся» в конечном виде.

8. Определённый интеграл.

Определённый интеграл как предел интегральной суммы. геометрический и физический смыслы определённого интеграла. Необходимые и достаточные условия интегрируемости. Интегрируемость непрерывной функции. Интегрируемость монотонной функции. Основные свойства определённого интеграла. Теорема о среднем. Существование первообразной функции. Формула Ньютона-Лейбница. Интегрирование подстановкой и по частям. Интегрирование чётных и нечётных функций в симметричных пределах.


9. Приложения определённого интеграла.

Вычисление площадей плоских фигур в полярных и декартовых координатах. Вычисление длины дуги плоской кривой. Вычисление объема тела вращения. Вычисление площади поверхности вращения.

10. Несобственные интегралы.

Понятие несобственного интеграла. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода).

Тема 4. Ряды.

11. Числовые ряды.

Числовой ряд и его частичные суммы. Сходящиеся ряды. Сложение рядов и умножение ряда на число. Остаток сходящегося ряда. Необходимое условие сходимости числового ряда. Гармонический ряд. Критерий Коши. Необходимое и достаточное условия сходимости ряда с положительными членами. Признаки Даламбера и Коши. Интегральный признак сходимости. Знакочередующиеся и знакопеременные ряды. Признак Лейбница. Абсолютная и условная сходимости числовых рядов.

12. Функциональные ряды.

Функциональный ряд и область его сходимости. Равномерная сходимость. Необходимый и достаточный признак равномерной сходимости. Сумма равномерно сходящегося ряда непрерывных функций.

Понятие степенного ряда. Теорема Абеля. Интервал и радиус сходимости. Равномерная сходимость степенного ряда.

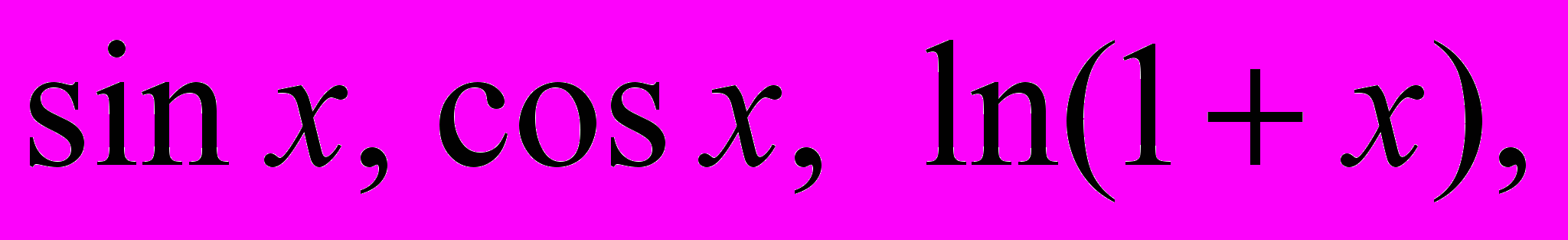
Разложение функций в степенной ряд. Ряд Тейлора (Маклорена). Разложение функций 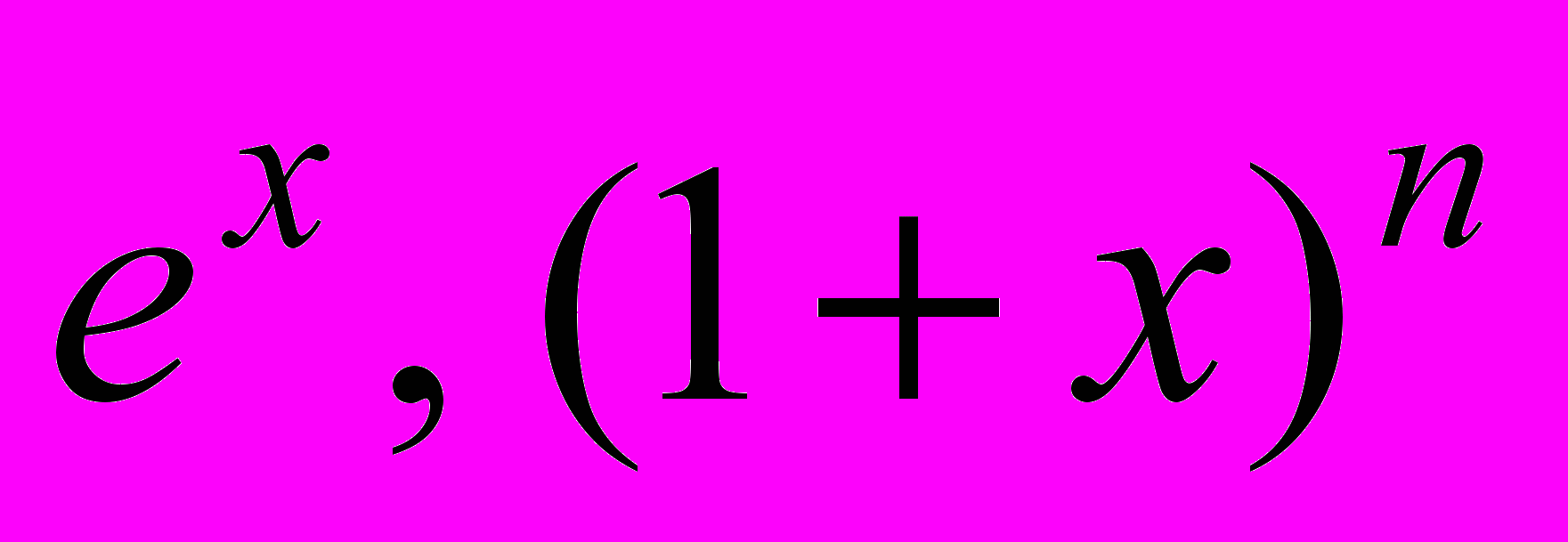в степенной ряд. Приближенное вычисление значений функций и интегралов с помощью степенных рядов.

13. Тригонометрические ряды. Ряд Фурье.

Тригонометрический ряд. Достаточные признаки разложимости в ряд Фурье. Разложение в ряд Фурье непериодической функции. Ряд Фурье для чётных и нечётных функций. Ряды Фурье для функций любого периода. Ряд Фурье по ортогональной системе функций.

Тема 5. Элементы функционального анализа.

14. Метрические пространства.

Определение и примеры метрических пространств. Окрестности точки. Предельные точки множества. Внутренность, замыкание и границы множества. Открытые и замкнутые множества. Отображения метрических пространств. Предел, непрерывность. Полные метрические пространства. Теорема Банаха о сжимающем отображении.


15. Нормированные пространства.

Линейные пространства. Линейные функционалы. Нормированные пространства. Полные нормированные пространства. Непрерывные линейные операторы. Линейные пространства со скалярным произведением. Неравенство Коши-Буняковского. Гильбертово пространство. Пространство Rn.

Тема 6. Дифференциальное исчисление функций нескольких переменных.

16. Функции нескольких переменных.

Действительная функция n действительных переменных как функция точки пространства Rn. График функции двух переменных, линии уровня. Предел функции нескольких переменных, повторные пределы. Непрерывность функции нескольких переменных.

17. Дифференцирование функции нескольких переменных.

Частные производные, дифференцируемость и дифференциал функции нескольких переменных. Достаточное условие дифференцируемости. Частные производные высших порядков. Равенство смешанных производных. Дифференциалы высших порядков. Производная сложной функции. Инвариантность формы полного дифференциала. Производная по направлению. Градиент.

18. Геометрический смысл функции нескольких переменных.

Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала функции двух переменных. Дифференцирование неявной функции.

19. Экстремум функции нескольких переменных.

Определение максимума и минимума. Необходимые и достаточные условия экстремума. Наибольшее и наименьшее значения функции в замкнутой области. Условные экстремумы.

Тема 7. Интегральное исчисление функций нескольких переменных.

20. Двойной и тройной интегралы.

Понятие двойного интеграла. Геометрический и физический смыслы двойного интеграла. Основные свойства двойного интеграла. Вычисление двойного интеграла в декартовых координатах. Вычисление двойного интеграла в полярных координатах.

Понятие тройного интеграла. Вычисление тройного интеграла в декартовых координатах. Вычисление тройного интеграла в сферических и цилиндрических координатах.


21. Применение кратных интегралов.

Вычисление объёмов тел. Вычисление площадей гладких поверхностей. Отыскание статистических моментов и центра тяжести.

22. Криволинейные интегралы.

Задача о работе плоского силового поля. Криволинейный интеграл и его основные свойства. Вычисление криволинейных интегралов. Формула Остроградского-Грина. Криволинейные интегралы, зависящие только от начала и конца пути интегрирования.

Тема 8. Дифференциальные уравнения и их системы.

23. Общие сведения о дифференциальных уравнениях.

Основные понятия теории дифференциальных уравнений. Задачи, приводящие к дифференциальным уравнениям.

24. Дифференциальные уравнения первого порядка.

Основные понятия теории дифференциальных уравнений первого порядка. Теорема единственности решения задачи Коши для уравнения первого порядка. Особые решения. Уравнения с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные уравнения. Уравнение Я. Бернулли. Уравнение в полных дифференциалах. Интегрирующий множитель. Уравнения Лагранжа и Клеро.

25. Дифференциальные уравнения высших порядков.

Основные понятия. Уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения второго и n-го порядков. Интегрирование линейных однородных дифференциальных уравнений второго и n-го порядков с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения. Структура общего решения линейного неоднородного дифференциального уравнения второго порядка. Метод вариации произвольных постоянных. Интегрирование линейных неоднородных дифференциальных уравнений второго и n-го порядков с постоянными коэффициентами и правой частью специального вида.

26. Системы дифференциальных уравнений.

Основные понятия. Интегрирование нормальных систем. Системы линейных дифференциальных уравнений с постоянными коэффициентами.

27. Дифференциальные уравнения с частными производными.

Уравнения с частными производными первого порядка. Связь характеристик с решениями. Теорема существования и единственности решения задачи Коши в случае двух независимых переменных.


III . РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ

    1. Распределение часов курса по темам и видам работ




№
Наименование тем и разделов
Всего часов
Ауд. занятия
Сам. раб.

ЛК
ПЗ
ЛБ

1 семестр




Тема 1. Введение в

математический анализ.
46
16
16
-
14

1.
Множества.

Действительные числа.
6
2
2
-
2

2.
Функции.
12
4
4
-
4

3.
Предел.
16
6
6
-
4

4.
Непрерывность функции.
12
4
4
-
4




Тема 2. Дифференциальное исчисление функций одной переменной.
38
14
14
-
10

5.
Производная и дифференциал.
22
8
8
-
6

6.
Основные теоремы дифференциального исчисления и их приложения.
16
6
6
-
4




Тема 3. Интегральное исчисление функций одной переменной.
62
22
22
-
18

7.
Неопределённый интеграл.
22
8
8
-
6




Итого за 1 семестр
106
38
38
-
30

2 семестр

8.
Определённый интеграл.
18
6
6
-
6

9.
Приложения определённого интеграла.
14
4
6
-
4

10.
Несобственные интегралы.
8
4
2
-
2




Тема 4. Ряды.
62
22
22
-
18

11.
Числовые ряды.
16
6
6
-
4

12.
Функциональные ряды.
30
12
10
-
8

13.
Тригонометрические ряды.

Ряд Фурье.
16
4
6
-
6




Итого за 2 семестр
102
36
36
-
30











































3 семестр




Тема 5. Элементы

функционального анализа.
22
8
6
-
8

14.
Метрические пространства.
12
4
4
-
4

15.
Нормированные пространства.
10
4
2
-
4




Тема 6. Дифференциальное исчисление функций

нескольких переменных.
34
11
13
-
10

16.
Функции нескольких переменных.
8
2
4
-
2

17.
Дифференцирование функций нескольких переменных.
12
4
4
-
4

18.
Геометрический смысл функции нескольких переменных.
6
2
2
-
2

19.
Экстремум функции нескольких переменных.
8
3
3
-
2




Итого за 3 семестр
56
19
19
-
18

4 семестр




Тема 7. Интегральное исчисление функций нескольких переменных.
52
18
18
-
16

20.
Двойной и тройной интегралы.
20
6
8
-
6

21.
Применение кратных интегралов.
16
6
6
-
4

22.
Криволинейные интегралы.
16
6
4
-
6




Итого за 4 семестр
52
18
18
-
16

5 семестр




Тема 8. Дифференциальные уравнения и их системы.
54
19
19
-
16

23.
Общие сведения о дифференциальных уравнениях.
6
2
2
-
2

24.
Дифференциальные уравнения первого порядка.
16
6
6
-
4

25.
Дифференциальные уравнения высших порядков.
21
7
8
-
6

26.
Системы дифференциальных уравнений.
6
2
2
-
2

27.
Дифференциальные уравнения с частными производными.
5
2
1
-
2




Итого за 5 семестр
54
19
19
-
16




Всего
370
130
130
-
110


3.2. Практические занятия, их содержание и объем в часах


№
Наименование тем и разделов
Кол-во часов




1 семестр
38

1.
Действительные числа. Модуль действительного числа.

2

2.
Функции и их свойства.
2

3.
Действительная функция действительной переменной. График функции.
2

4.
Предел числовой последовательности.
2

5.
Предел функции.
2

6.
Основные замечательные пределы. Бесконечно малые и бесконечно большие. Сравнение бесконечно малых.
2

7.
Непрерывность функции в точке и на промежутке. Непрерывность суммы, произведения и частного. Односторонняя непрерывность. Классификация точек разрыва.
2

8.
Контрольная работа.
2

9.
Дифференцирование суммы, произведения и частного. Дифференцирование сложной функции. Производная обратной функции.
2

10.
Производные и дифференциалы высших порядков.

2

11.
Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование.
2

12.
Касательная и нормаль к графику функции.
2

13.
Постоянство, возрастание и убывание функции на промежутке. Экстремумы функции.

2

14.
Наибольшее и наименьшее значения функции на отрезке. Точки перегиба, асимптоты.
2

15.
Исследование функций и построение графиков функций.
2

16.
Таблица основных интегралов. Непосредственное интегрирование. Интегрирование по частям и заменой переменной.
2

17.
Интегрирование рациональных функций.
2

18.
Интегрирование иррациональных и тригонометрических функций.
2

19.
Контрольная работа.
2




2 семестр
36

1.
Определённый интеграл. Формула Ньютона – Лейбница.
2

2-3.
Интегрирование по частям и заменой переменной.

4

4.
Вычисление площадей плоских фигур в декартовых и полярных координатах.
2

5.
Вычисление объёмов тел вращения.

2

6.
Вычисление длины дуги. Вычисление площади поверхности вращения.
2

7.
Вычисление несобственных интегралов.
2

8.
Числовой ряд и его частичные суммы. Сходимость числовых рядов. Гармонический ряд. Сравнение рядов с положительными членами.
2

9.
Контрольная работа.
2

10.
Признаки Даламбера и Коши. Интегральный признак сходимости. Абсолютно и условно сходящиеся ряды.
2

11.
Функциональный ряд и область его сходимости. Равномерная сходимость.
2

12.
Степенной ряд. Интервал и радиус сходимости. Равномерная сходимость степенного ряда.
2

13-14.
Разложение функций в степенной ряд. Ряд Тейлора и Маклорена.
4

15.
Приближенное вычисление значений функций и интегралов с помощью степенных рядов.
2

16-17.
Разложение функций в ряд Фурье.
4

18.
Контрольная работа
2




3 семестр
19

1-2.
Метрические пространства.
4

3.
Нормированные пространства.
2

4.
Предел функции нескольких переменных, повторные пределы. Непрерывность функции нескольких переменных.
2

5.
Контрольная работа
2

6.
Частные производные, дифференцируемость и дифференциал функции нескольких переменных.
2

7.
Дифференцирование сложных функций. Инвариантность формы дифференциала первого порядка. Производная по направлению. Градиент
2

8.
Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала функции двух переменных. Дифференцирование неявной функции.
2

9-10.
Экстремум функции двух переменных. Нахождение наибольшего и наименьшего значений. Условные экстремумы.
3




4 семестр
18

1-2.
Вычисление двойного интеграла в декартовых и полярных координатах.

4

3.
Вычисление тройного интеграла в декартовых координатах.

2

4.
Вычисление тройного интеграла в сферических и цилиндрических координатах.
2

5.
Контрольная работа.
2

6-7.
Вычисление объёмов тел и площадей гладких поверхностей.
4

8-9.
Вычисление криволинейных интегралов. Формула Остроградского-Грина. Криволинейные интегралы, зависящие только от начала и конца пути интегрирования.
4




5 семестр
19

1.
Общие сведения о дифференциальных уравнениях.
2

2.
Уравнения с разделяющимися переменными. Однородные уравнения первого порядка.
2

3.
Линейные дифференциальные уравнения первого порядка. Уравнения Я. Бернулли.
2

4.
Уравнение в полных дифференциалах. Интегрирующий множитель. Уравнения Лагранжа и Клеро.
2

5.
Контрольная работа.
2

6.
Уравнения, допускающие понижение порядка. Линейные однородные дифференциальные уравнения.
2

7.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
2

8.
Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами.
2

9.
Системы дифференциальных уравнений.
2

10.
Дифференциальные уравнения с частными производными.
1