Рабочая учебная программа дисциплины (модуля) Математический анализ
| Вид материала | Рабочая учебная программа |
- Рабочая программа дисциплины «Математический анализ ii» Направление, 132.24kb.
- Рабочая программа учебной дисциплины «Математический анализ» Направление подготовки, 275.11kb.
- Рабочая программа учебной дисциплины «Математический анализ» Специальность «Математические, 187.35kb.
- Примерная программа наименование дисциплины Математический анализ, 308.64kb.
- Рабочая программа дисциплины (модуля) «математический анализ», 424.74kb.
- Рабочая программа по дисциплине б 1математика. Математический анализ шифр и название, 259.57kb.
- Рабочая учебная программа (Syllabus) дисциплины Наименование дисциплины: социальная, 372.74kb.
- Рабочая программа по дисциплине с 1 Математический анализ, 302.06kb.
- Программа по дисциплине математический анализ, 133.35kb.
- Рабочая программа дисциплины «Математический анализ» Направление подготовки, 180.51kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«Ивановский государственный химико-технологический университет»
Институт управления, финансов и информационных систем
Кафедра высшей математики
Утверждаю: проректор по УР
_______________ В.В. Рыбкин
« » 200 г.
Рабочая учебная программа дисциплины (модуля)
Математический анализ
Направление подготовки
080100 Экономика
Профиль подготовки
Финансы и кредит
Квалификация (степень) Бакалавр
Форма обучения очная
Иваново, 2010
1. Цели освоения дисциплины «Математический анализ»
- дать студентам абстрактные понятия математического анализа, такие как функция, предел функции, бесконечно малая и бесконечно большая величина, производная и дифференциал функции, определенный интеграл, используемые для описания и моделирования различных по своей природе математических задач;
- дать представление о дифференциальных уравнениях и методах их решения;
- привить студентам навыки использования аналитических методов в практической деятельности;
- показать студентам универсальный характер основных понятий математического анализа для получения комплексного представления о подходах к созданию математических моделей технических систем и объектов.
2. Место дисциплины в структуре ООП бакалавриата
Дисциплина «Математический анализ» входит в базовую часть математического и естественнонаучного цикла подготовки бакалавра по направлению «Экономика».
Логическая и содержательно – методическая взаимосвязь с другими дисциплинами и частями ООП выражается в следующем.
Дисциплине «Математический анализ» предшествует общематематическая подготовка в объеме средней общеобразовательной школы или технического колледжа, а также дисциплина.
- Линейная алгебра
В результате освоения предшествующих дисциплин студент должен:
знать:
- основные понятия и методы элементарной математики, геометрии, алгебры и начал математического анализа;
- основные понятия линейной алгебры;
уметь:
- производить действия с числами;
- использовать основные алгебраические тождества для преобразования алгебраических выражений;
- использовать тригонометрические тождества для преобразования тригонометрических выражений;
- решать линейные и квадратичные уравнения и неравенства;
- решать тригонометрические уравнения;
- выполнять геометрические построения;
- доказывать математические утверждения;
- вычислять определители;
- выполнять действия над матрицами;
владеть:
- приемами вычислений на калькуляторе инженерного типа;
- навыками использования математических справочников.
Освоение данной дисциплины как предшествующей необходимо при изучении следующих дисциплин:
- Теория вероятностей и математическая статистика;
- Методы оптимальных решений;
- Финансовые вычисления;
- Эконометрика.
3. Компетенции обучающегося, формируемые в результате освоения
дисциплины «Математический анализ»
- владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения (ОК-1);
- способность собрать и проанализировать исходные данные, необходимые для Расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1);
- способность на основе типовых методик и действующей нормативно-правовой базы рассчитать экономические и социально-экономические показатели, характеризующие деятельность хозяйствующих субъектов (ПК-2);
- способность выполнять необходимые для составления экономических разделов планов расчеты, обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3);
- способность осуществлять сбор анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК–4);
- способность выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы;
- способность на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты;
В результате освоения дисциплины студент должен:
знать:
- основные понятия и методы математического анализа, теории дифференциальных уравнений;
уметь:
- применять математические методы при решении профессиональных задач повышенной сложности, учитывая границы применимости математической модели;
- решать типовые задачи по основным разделам курса;
владеть:
- методами построения математической модели профессиональных задач и содержательной интерпретации полученных результатов.
4. Структура дисциплины «Математический анализ»
Общая трудоемкость дисциплины составляет 7 зачетные единицы, 252 часа.
| Вид учебной работы | Всего часов | Семестры | |
| 1 | 2 | ||
| Аудиторные занятия (всего) | 102 | | |
| В том числе: | | | |
| Лекции | 51 | | 51 |
| Практические занятия (ПЗ) | 51 | | 51 |
| Семинары (С) | - | | |
| Лабораторные работы (ЛР) | - | | |
| Самостоятельная работа (всего) | 150 | | 150 |
| В том числе: | | | |
| Курсовой проект (работа) | - | | |
| Расчетно-графические работы | 40 | | 40 |
| Оформление отчетов по лабораторным работам | - | | |
| Реферат | - | | |
| Подготовка к текущим занятиям, коллоквиумам | 90 | | 90 |
| Подготовка к экзамену | 20 | | 20 |
| Вид промежуточной аттестации (зачет, экзамен) | | | зачет экзамен |
| Общая трудоемкость часов зач. ед. | 252 | | |
| 7 | | | |
5. Содержание дисциплины
5.1. Содержание разделов дисциплины
| № п/п | Наименование раздела дисциплины | Содержание раздела |
| 1. | Введение в анализ | Операции над множествами. Основные числовые множества. Функции одной переменной. Основные элементарные функции, их графики. Сложная функция. Последовательности, предел числовой последовательности. Теоремы о пределах. Признаки существования пределов. Первый и второй замечательный пределы. Бесконечно малые и бесконечно большие величины, связь между ними. Сравнение бесконечно малых величин. Раскрытие неопределенностей. Непрерывность функций. Точки разрыва. Классификация точек разрыва. Теоремы о непрерывных функциях на отрезке. Непрерывность элементарных функций. |
| 2. | Дифференциальное исчисление функций одного переменного. | Производная: определение, механический и геометрический смысл. Уравнение касательной к кривой. Дифференцируемость функций, связь непрерывности с дифференцируемостью. Обратная функция и ее дифференцирование. Таблица основных правил и формул дифференцирования. Производные высших порядков. Дифференциал функции, его применение в приближенных вычислениях. Достаточные признаки монотонности функции. Экстремумы функции, необходимое и достаточные условия. Выпуклость кривой, точки перегиба. Необходимое и достаточные условия. Асимптоты кривой. |
| 3. | Интегральное исчисление функций одной переменной. | Определение первообразной. Теорема о бесконечном множестве первообразных для данной функции. Понятие неопределенного интеграла. Таблица основных интегралов. Основные свойства неопределенного интеграла. Интегрирование методами замены переменной и по частям. Рациональные дроби и их интегрирование. Понятие определенного интеграла и его основные свойства. Теорема о среднем. Площадь криволинейной трапеции. Производная определенного интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница. Вычисление определенного интеграла методами замены переменной и по частям. Несобственные интегралы. Приложения определенного интеграла: площадь фигуры в декартовых координатах, объем тела вращения, длина дуги плоской кривой, работа переменной силы. |
| 4. | Функции нескольких переменных. Элементы теории функций комплексного переменного. | Область определения и график функции двух переменных. Линии и поверхности уровня. Частные производные и дифференциалы. Полное приращение и полный дифференциал, его применение. Производная сложной функции, производная неявно заданной функции. Уравнение касательной к кривой 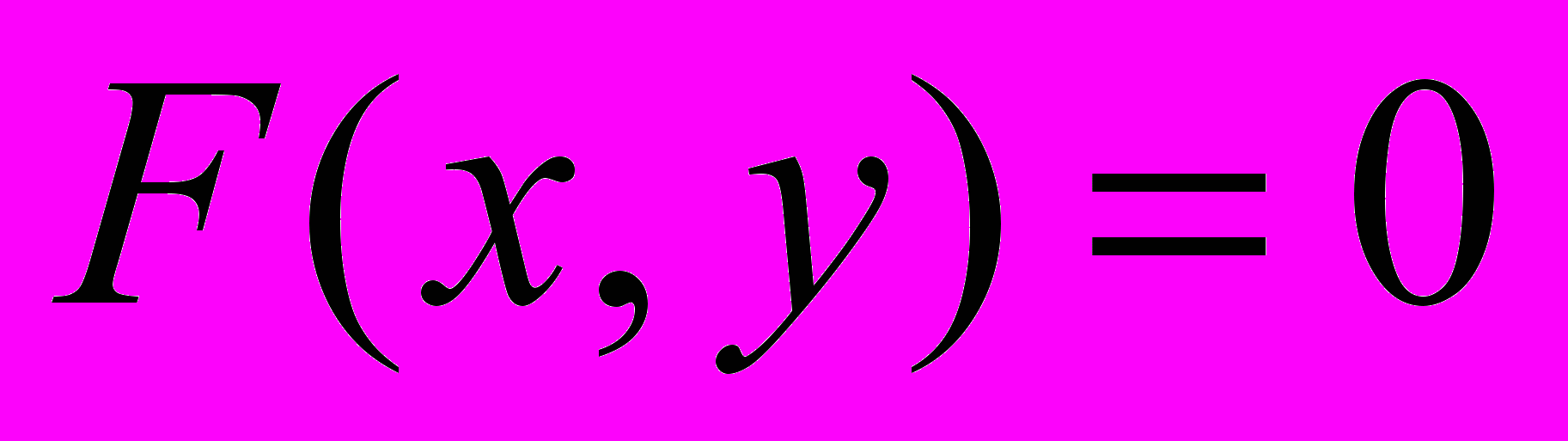 . Уравнение касательной плоскости к поверхности . Уравнение касательной плоскости к поверхности 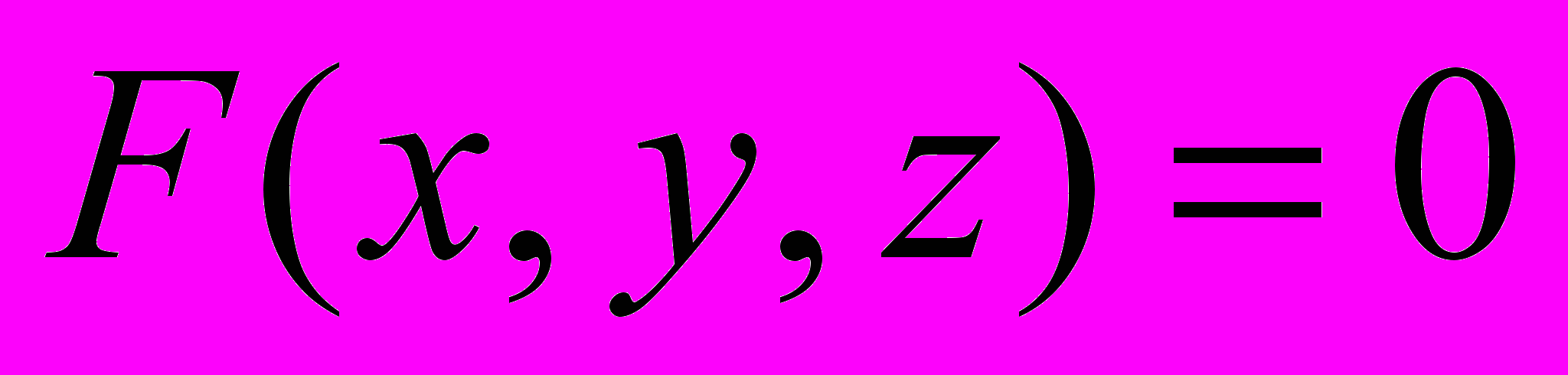 . Производная по направлению. Градиент. . Производная по направлению. Градиент.Частные производные высших порядков. Экстремумы функции двух переменных. Условные экстремумы; наибольшее и наименьшее значения функции 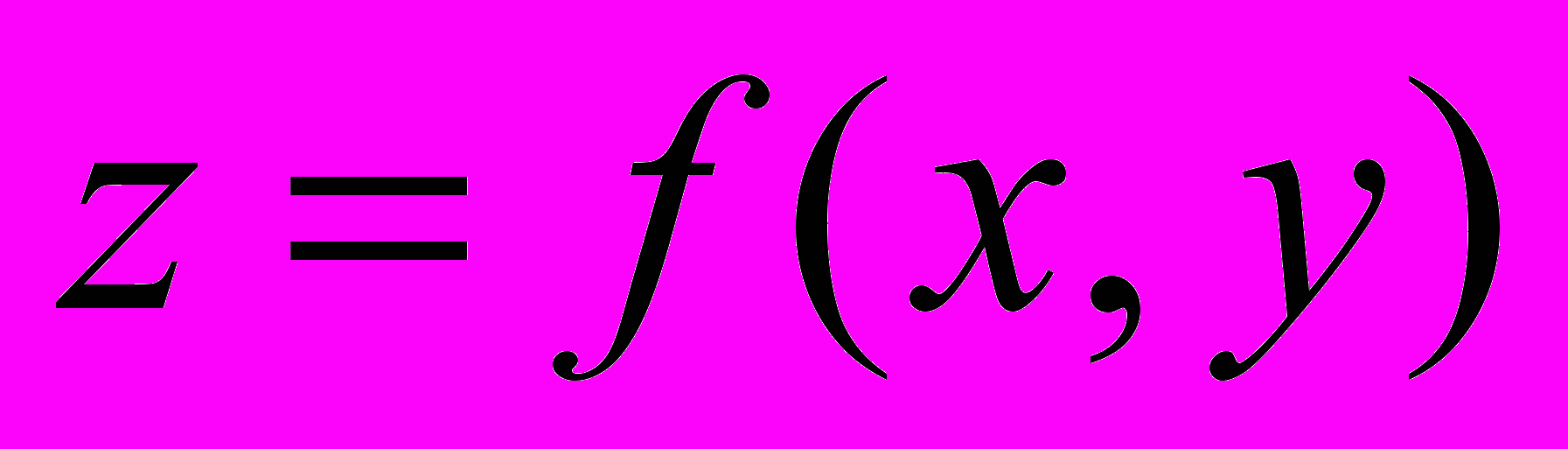 в замкнутой ограниченной области. в замкнутой ограниченной области.Элементы теории функций комплексного переменного. Комплексные числа, алгебраические действия над ними. Основные трансцендентные функции. Формулы Эйлера. |
| 5. | Дифференциальные уравнения | Примеры задач, приводящих к дифференциальным уравнениям. Дифференциальное уравнения 1-го порядка: общее и частное решение (интеграл), задача Коши, формулировка теоремы существования и единственности решения уравнения 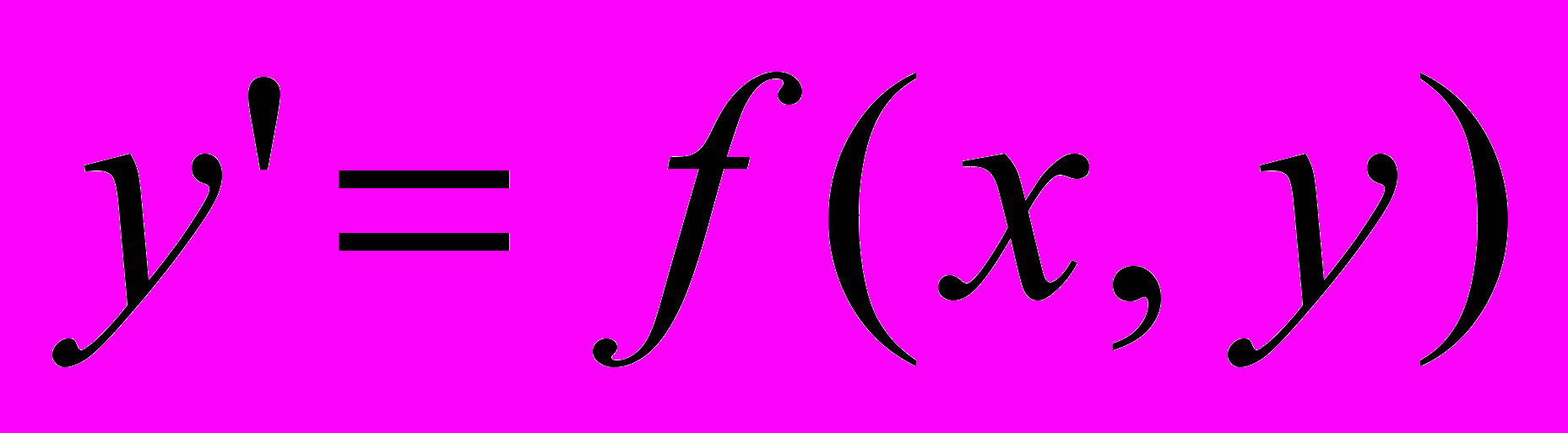 . . Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Линейные дифференциальные уравнения 1-го порядка и уравнения Бернулли. Дифференциальные уравнения 2-го порядка: общее и частное решение (интеграл), задача Коши, формулировка теоремы существования и единственности решения уравнения 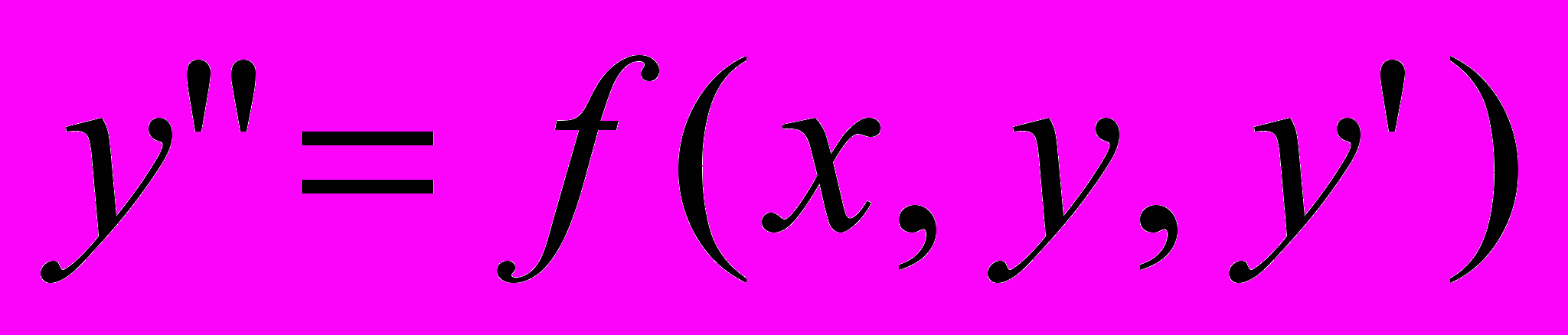 . . Дифференциальные уравнения 2-го порядка, допускающие понижение порядка. Линейные дифференциальные уравнения 2-го порядка: структура общего решения однородного и неоднородного уравнений. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Характеристическое уравнение. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и специальной правой частью. Системы дифференциальных уравнений. Нормальная форма системы. Отыскание решения системы методом сведения к одному дифференциальному уравнению. |
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспечиваемых (последующих) дисциплин | № № разделов (модулей) данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1. | Теория вероятностей и математическая статистика | + | + | + | | |
| 2. | Методы оптимальных решений | | + | | + | |
| 3. | Финансовые вычисления | + | | + | | + |
| 4. | Эконометрика | + | + | + | + | + |
5.3. Разделы дисциплины и виды занятий
| № п/п | Наименование раздела (модуля) дисциплины | Лекц. | Практ. зан. | Лаб. зан. | Семин | СРС | Все-го час. |
| 1. | Введение в анализ | 6 | 6 | | | 20 | 32 |
| 2. | Дифференциальное исчисление функций одного переменного. | 10 | 10 | | | 40 | 60 |
| 3. | Интегральное исчисление функций одной переменной. | 10 | 10 | | | 20 | 40 |
| 4. | Функции нескольких переменных . Элементы теории функций комплексного переменного. | 10 | 10 | | | 20 | 40 |
| 5. | Дифференциальные уравнения | 15 | 15 | | | 30 | 60 |
6. Лабораторный практикум
По данной дисциплине не предусматривается.
7. Практические занятия (семинары)
| № раздела дисциплины | Тематика практических занятий | Трудо-емкость (час.) |
| Раздел 1 | Элементарные функции. Вычисление пределов. Бесконечно малые и бесконечно большие величины. Сравнение б.м. Непрерывность функции. Точки разрыва функций. Контрольная работа №1 | 1 2 2 1 |
| Раздел 2 | Техника дифференцирования. Техника дифференцирования. Уравнение касательной. Механический смысл производной. Производные высших порядков. Дифференциал. Применение дифференциала. Исследование функций и построение графиков. Контрольная работа №2 | 2 2 2 2 2 |
| Раздел 3 | Таблица основных интегралов. Непосредственное интегрирование. Интегрирование методом подстановки. Интегрирование по частям. Замена переменной и интегрирование по частям в определенном интеграле. Вычисление площадей фигур. Несобственные интегралы с бесконечными пределами и от разрывных функций Контрольная работа №3 | 2 2 2 2 2 |
| Раздел 4 | Функции 2-х переменных, их графики. Линии уровня. Вычисление частных производных 1-го и 2-го порядков. Полный дифференциал, его применения в приближенных вычислениях. Экстремумы функций 2-х переменных. Производная по направлению. Градиент. | 2 2 2 2 2 |
| Раздел 5 | Понятие частного и общего решения. Решение простейших дифференциальных уравнений 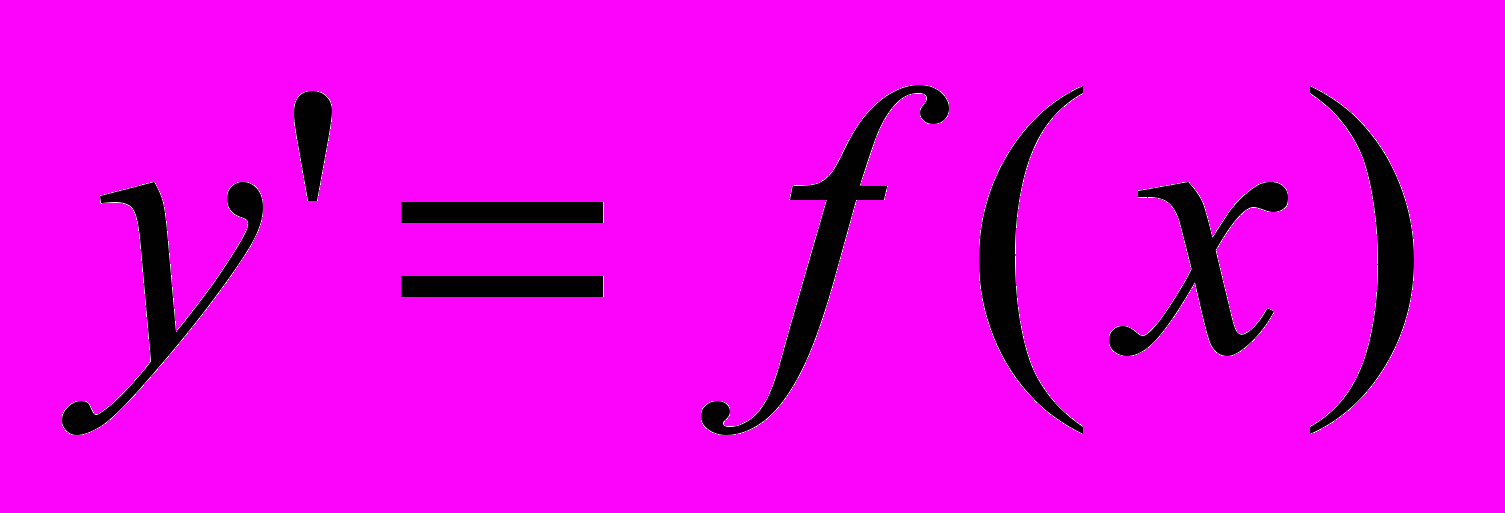 и и 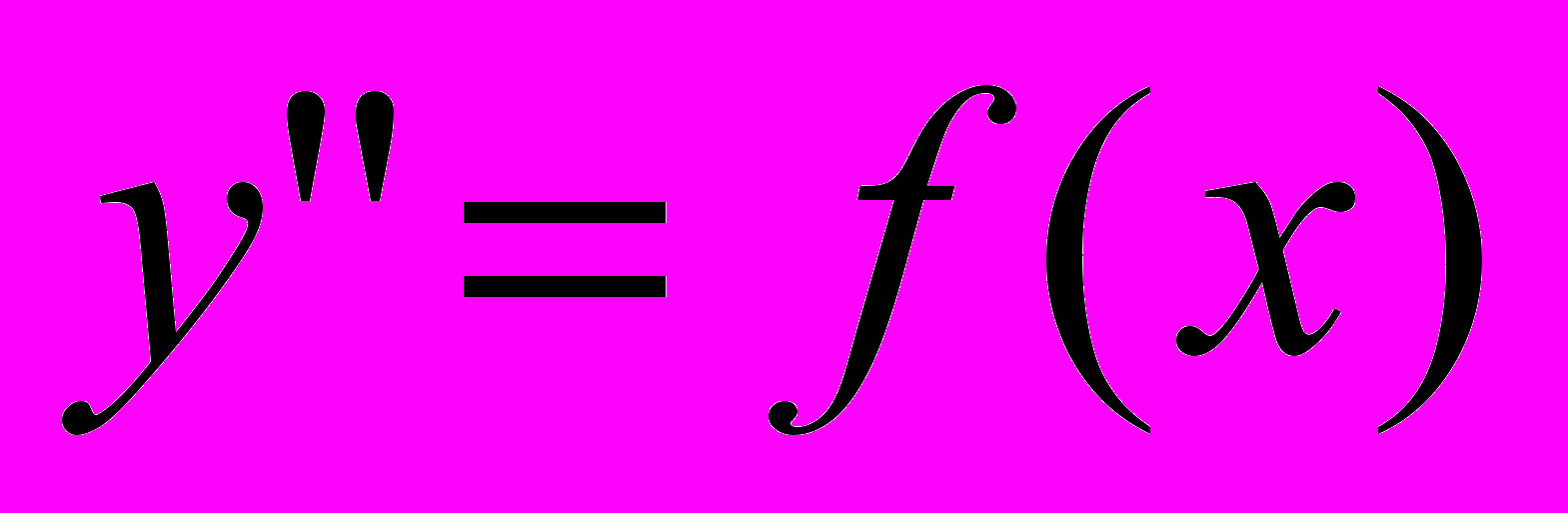 . .Уравнения 1-го порядка с разделяющимися переменными. Линейные уравнения 1-го порядка и уравнение Бернулли. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и специальной правой частью. Системы дифференциальных уравнений Контрольная работа №4 | 2 3 2 2 2 2 2 |
8. Примерная тематика курсовых проектов (работ)
По данной дисциплине курсовых проектов (работ) не предусматривается.
9. Образовательные технологии и методические рекомендации
по организации изучения дисциплины
Чтение лекций по данной дисциплине проводится традиционным способом.
Студентам предоставляется возможность для самоподготовки и подготовки к экзамену использовать электронный вариант конспекта лекций, подготовленный преподавателем в соответствие с планом лекций.
При работе используется диалоговая форма ведения лекций с постановкой и решением проблемных задач, обсуждением дискуссионных моментов и т.д.
При проведении практических занятий создаются условия для максимально самостоятельного выполнения заданий. Поэтому при проведении практического занятия преподавателю рекомендуется:
- Провести экспресс-опрос (устно или в тестовой форме) по теоретическому материалу, необходимому для выполнения работы (с оценкой).
- Проверить правильность выполнения заданий, подготовленных студентом дома (с оценкой).
Любой практическое занятие включает самостоятельную проработку теоретического материала и изучение методики решения типичных задач. Некоторые задачи содержат элементы научных исследований, которые могут потребовать углубленной самостоятельной проработки теоретического материала.
При организации внеаудиторной самостоятельной работы по данной дисциплине преподавателю рекомендуется использовать следующие ее формы:
- решение студентом самостоятельных задач обычной сложности, направленных на закрепление знаний и умений;
- выполнение индивидуальных заданий повышенной сложности, направленных на развитие у студентов научного мышления и инициативы.
10. Оценочные средства для текущего контроля успеваемости, промежуточной
аттестации по итогам освоения дисциплины и учебно-методическое обеспечение
самостоятельной работы студентов
Всего по текущей работе студент может набрать 50 баллов, в том числе:
- контрольные работы – всего 40 баллов;
- выполнение домашних самостоятельных заданий – 10 баллов.
Студент допускается к экзамену, если он набрал по текущей работе не менее 26 баллов. Минимальное количество баллов по каждому из видов текущей работы составляет половину от максимального.
Для обеспечения самостоятельной работы студентов предлагается одна домашняя расчетная работа с индивидуальными заданиями. Общее количество заданий по каждой работе - более 50.
Тематика домашних самостоятельных работ:
Домашняя расчетная работа №1. Исследовать данную функцию и построить ее график.
Пример задания.
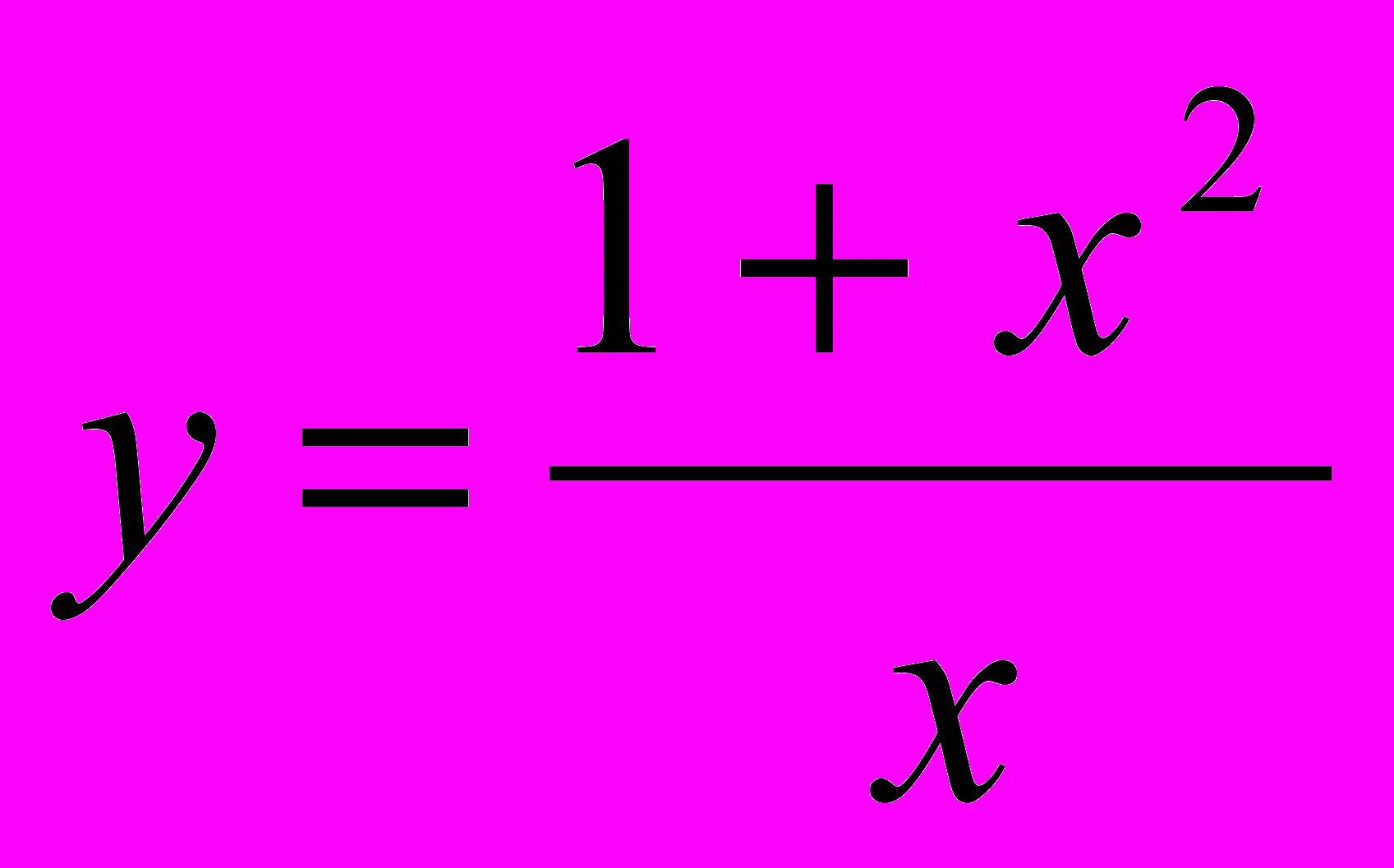
Указание. Исследование провести по следующему плану:
- Область определения.
- Множество значений.
- Четность/нечетность, периодичность/непериодичность.
- Точки разрыва. Поведение функции вблизи точек разрыва.
- Асимптоты функции.
- Интервалы монотонности.
- Точки экстремума.
- Интервалы постоянной выпуклости.
- Точки перегиба.
Тематика контрольных работ:
Контрольная работа № 1. Пределы функций.
Пример задания.
- Вычислить предел
1.1
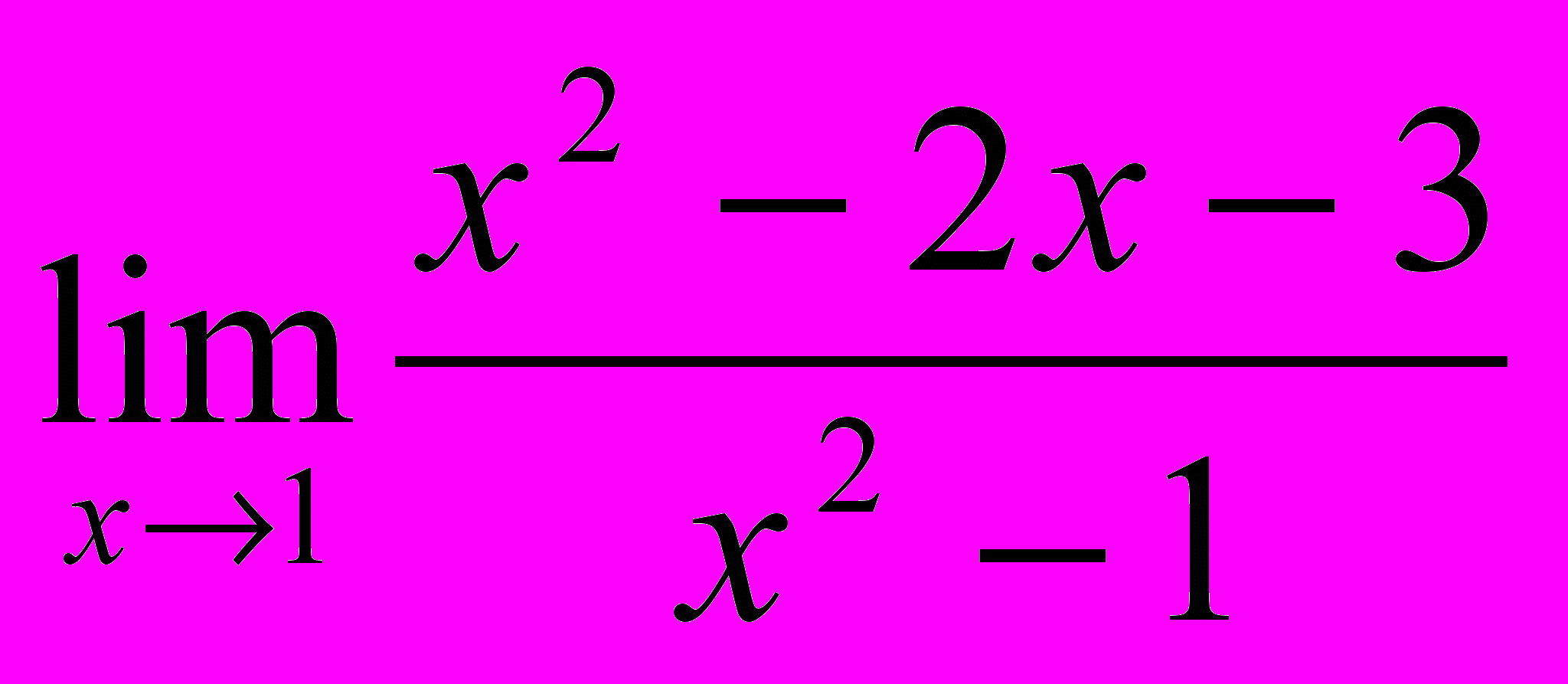
1.2
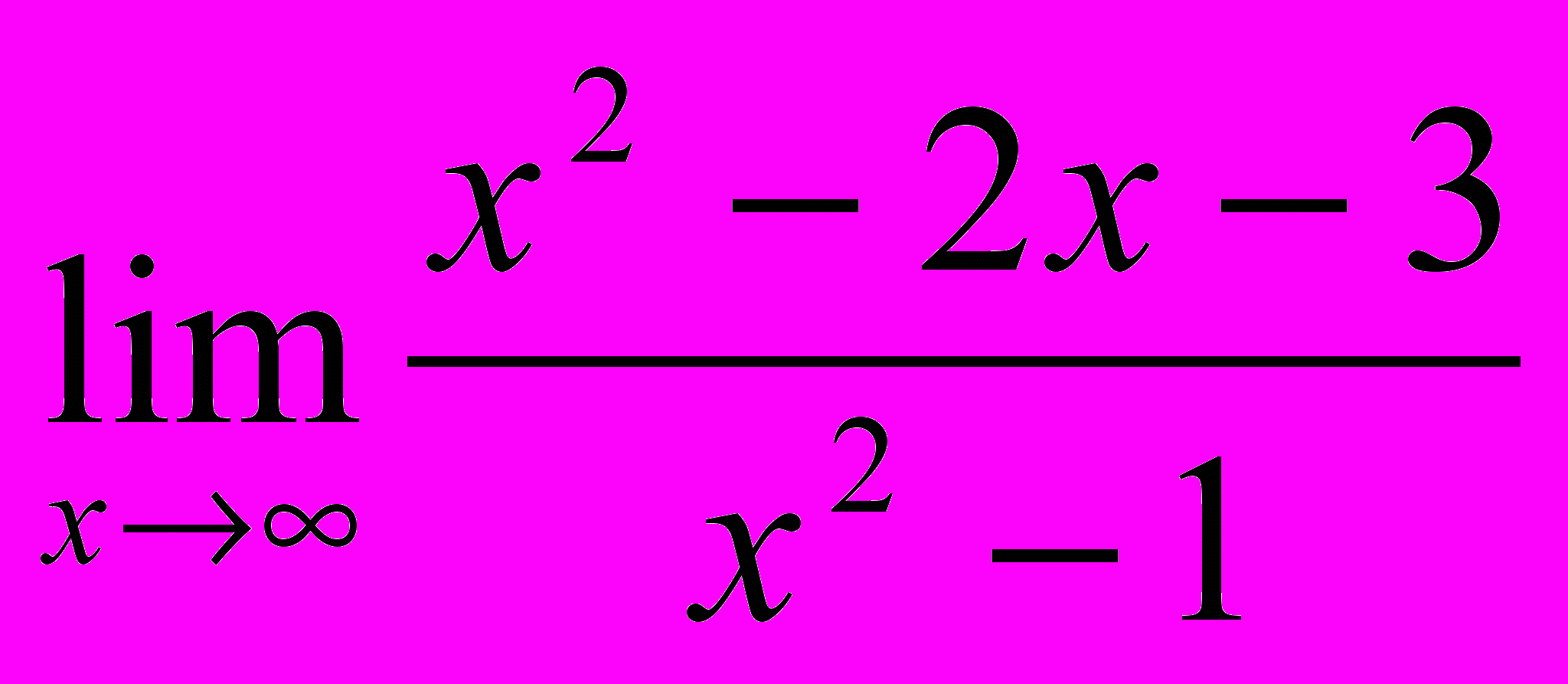
1.3
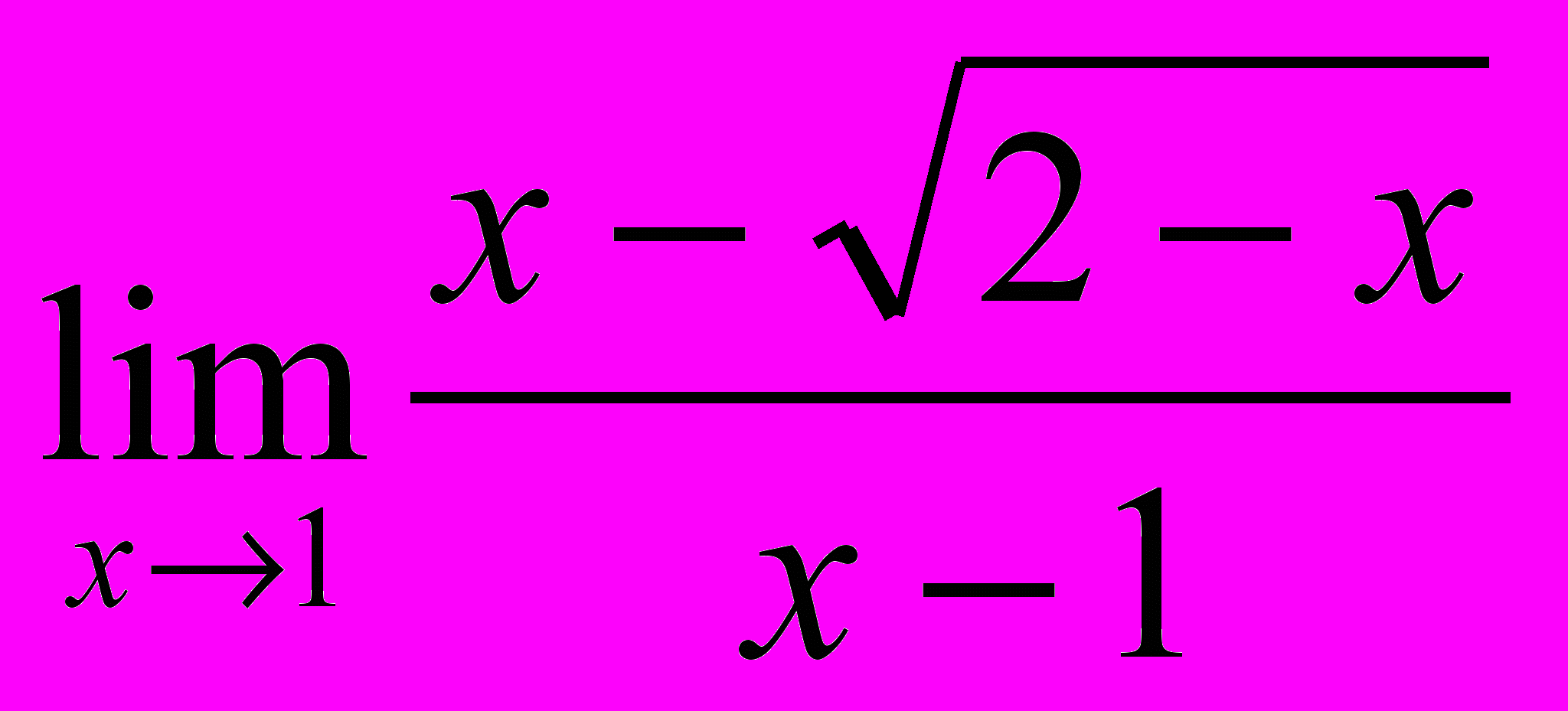
1.4
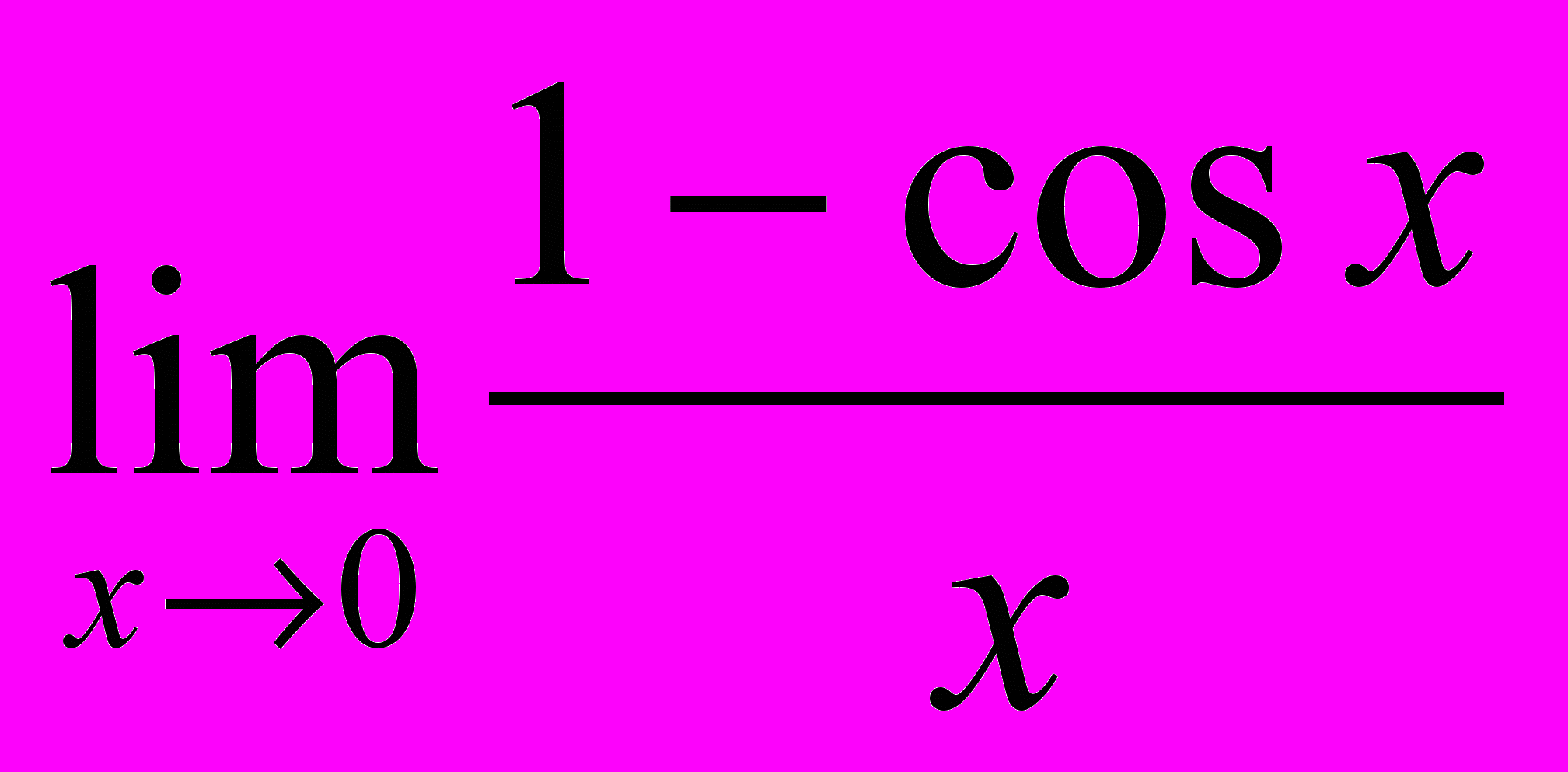
1.5
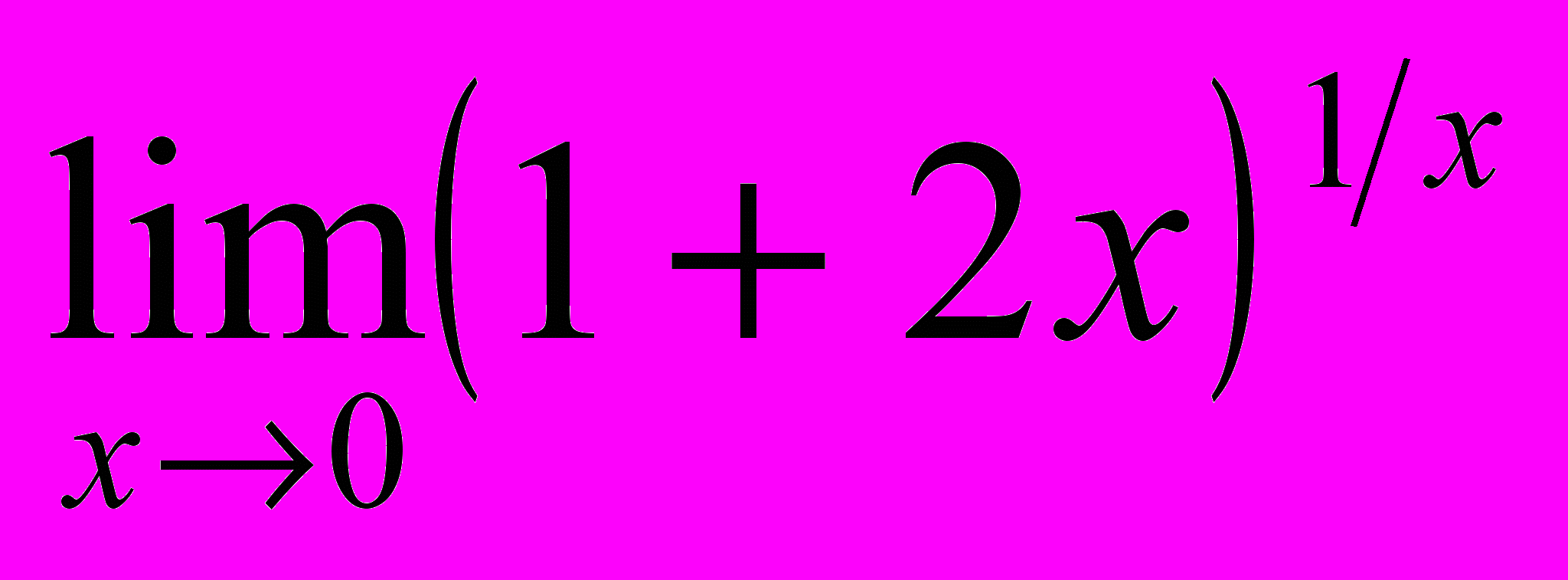
- Сравнить бесконечно малые
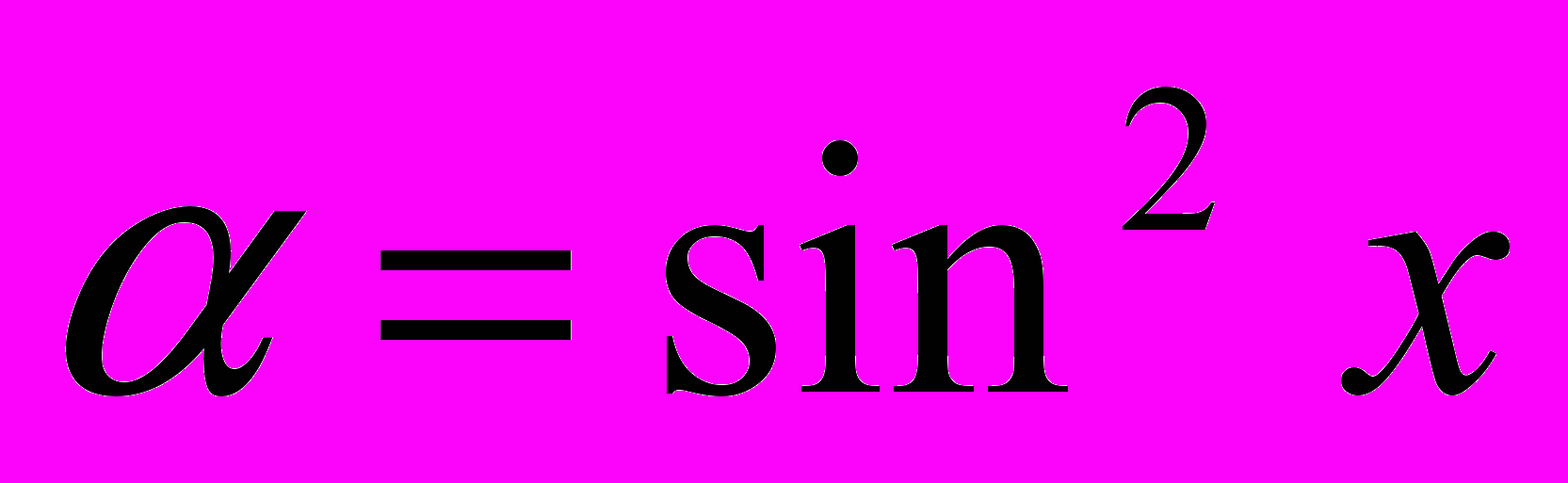 и
и 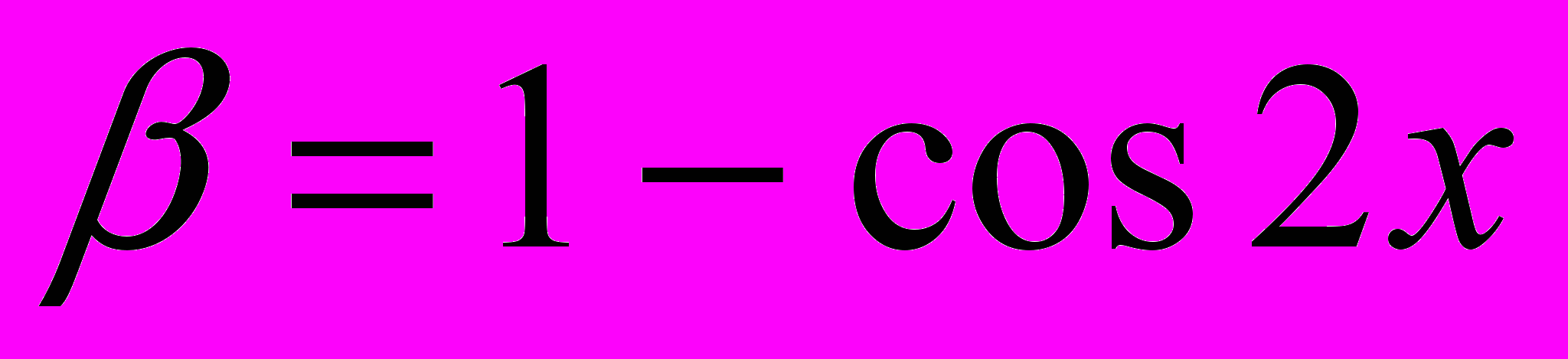 при
при 
- Найти точки разрыва функции и определить их род
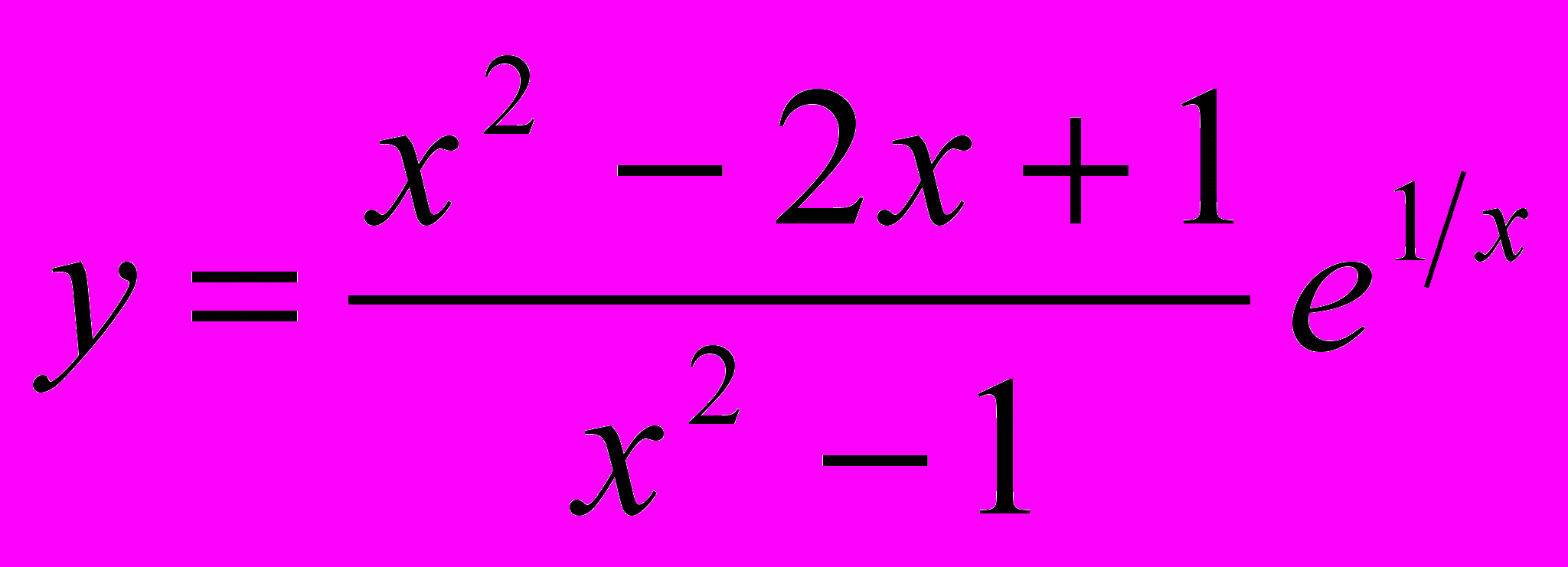
Контрольная работа № 2. Дифференциальное исчисление функций одной переменной.
Пример задания.
- Найти производные данных функций
1.1
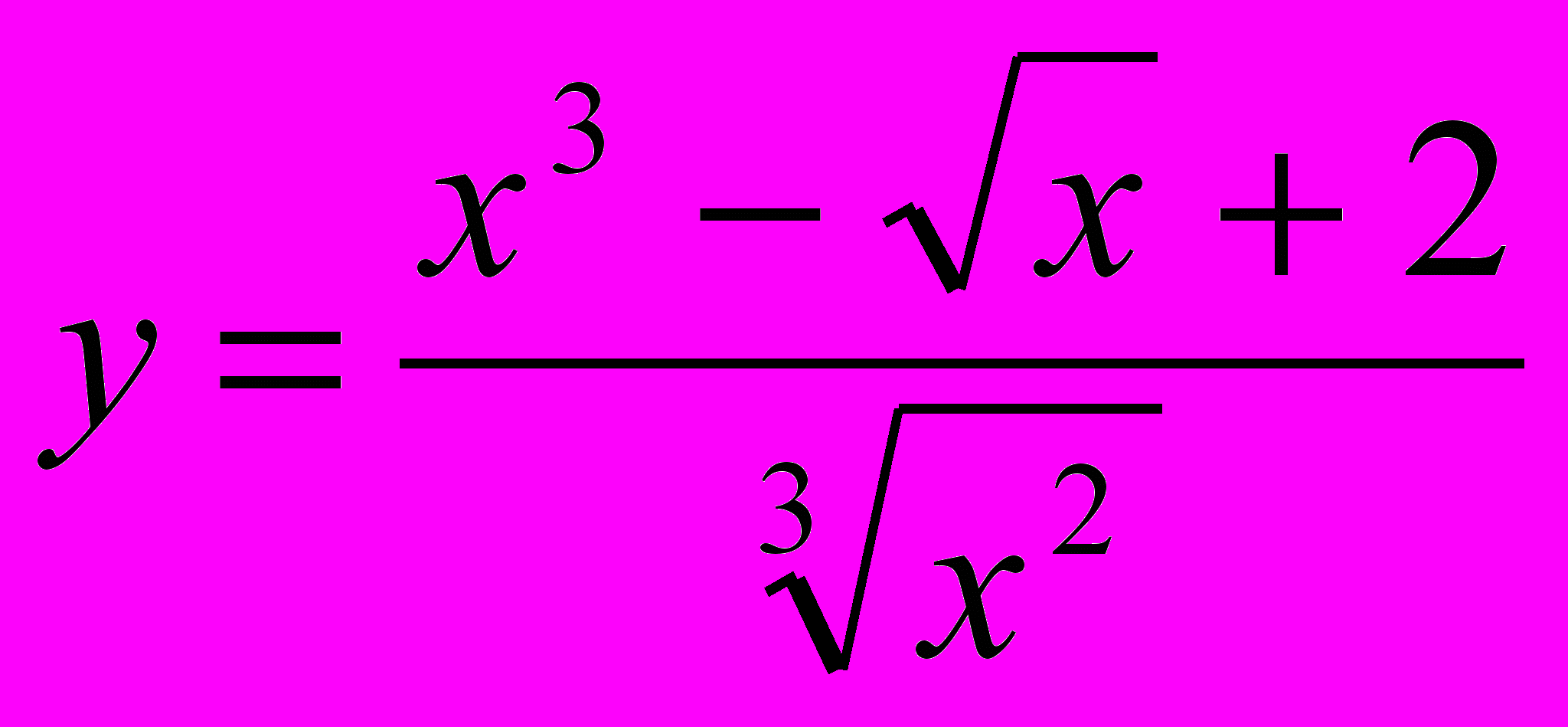 ,
, 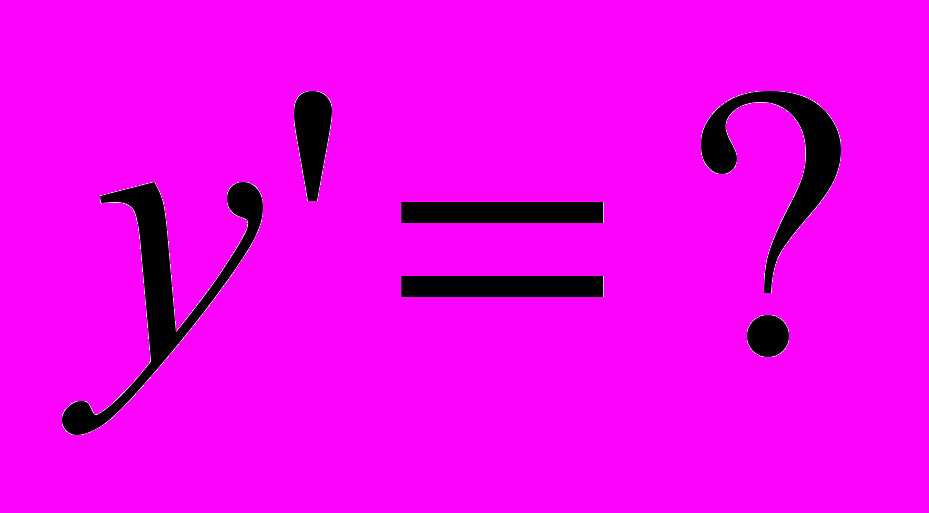
1.2
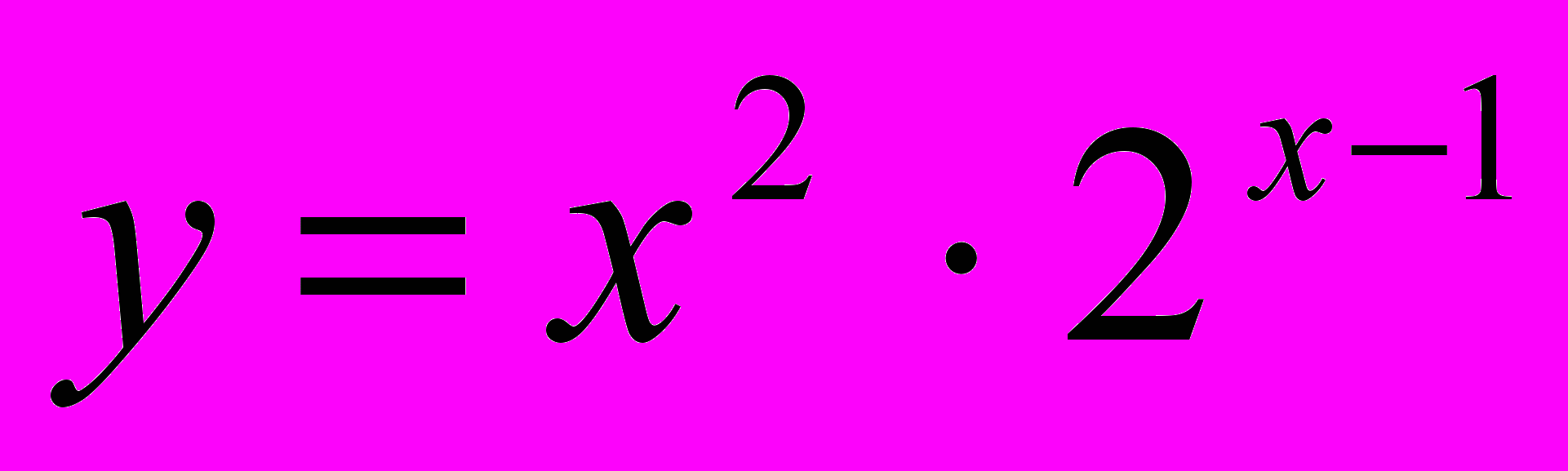 ,
, 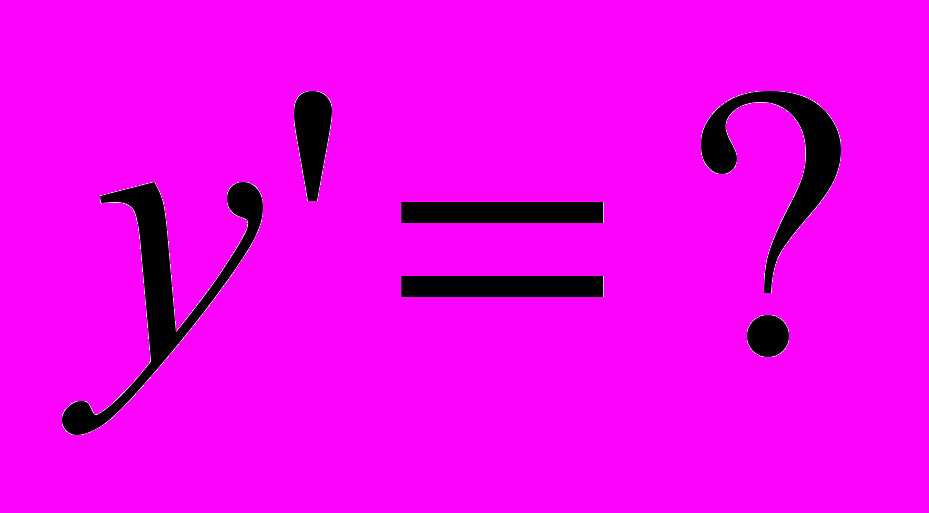
1.3
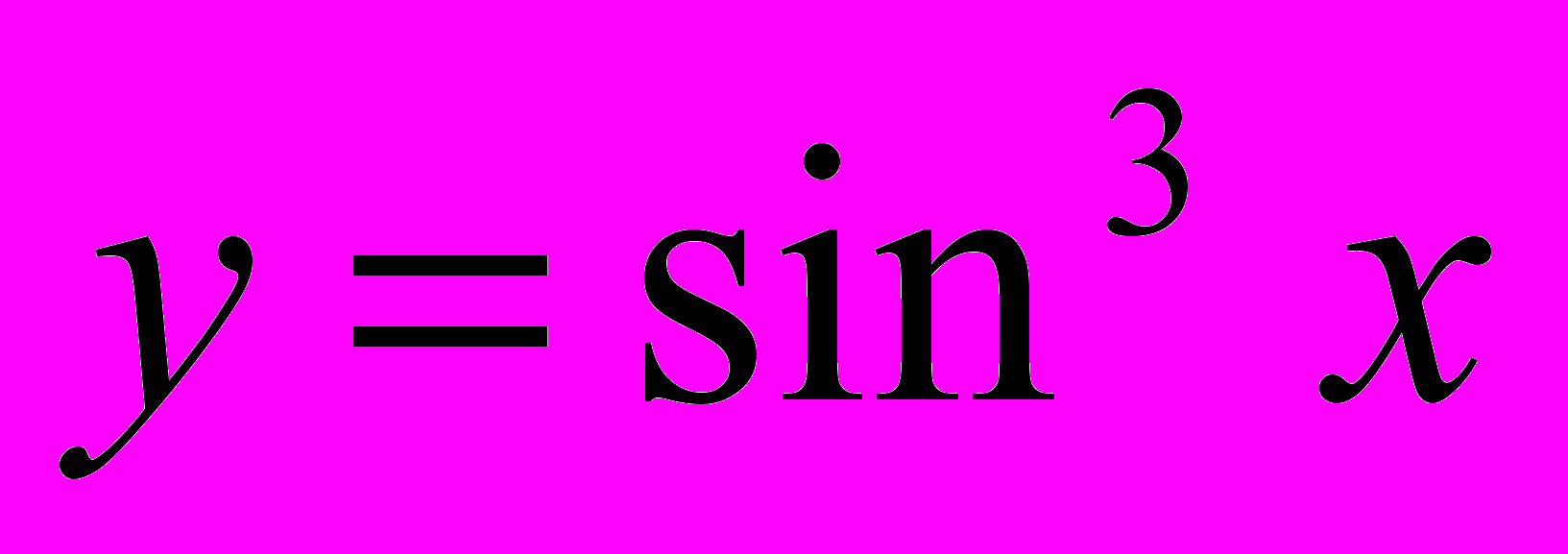 ,
, 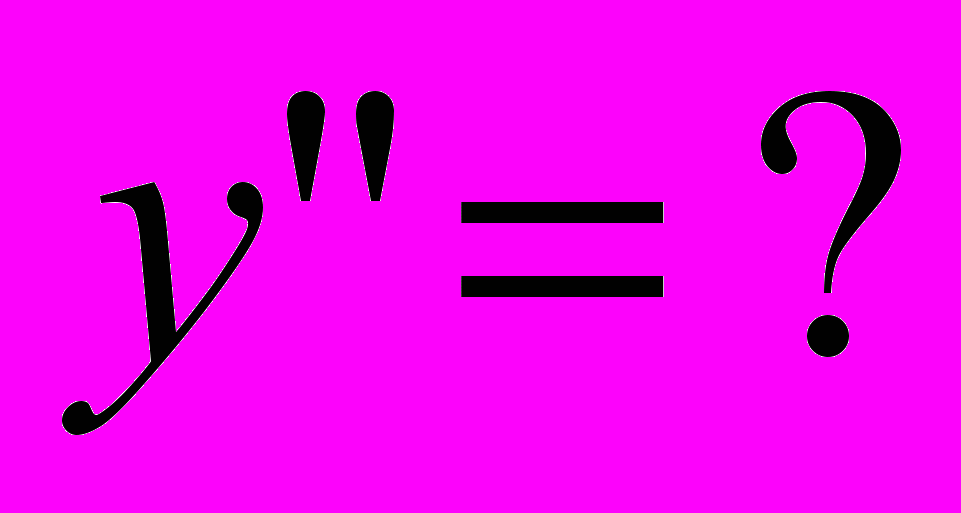
1.4
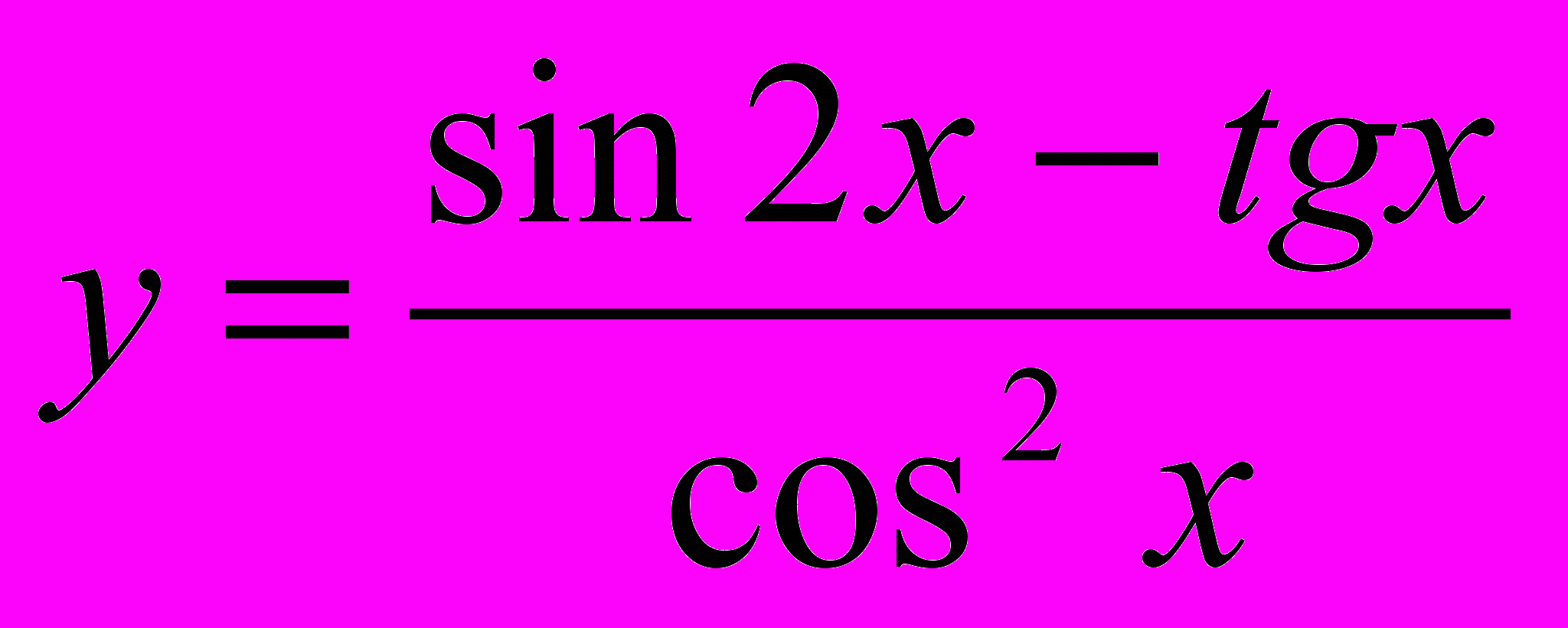 ,
, 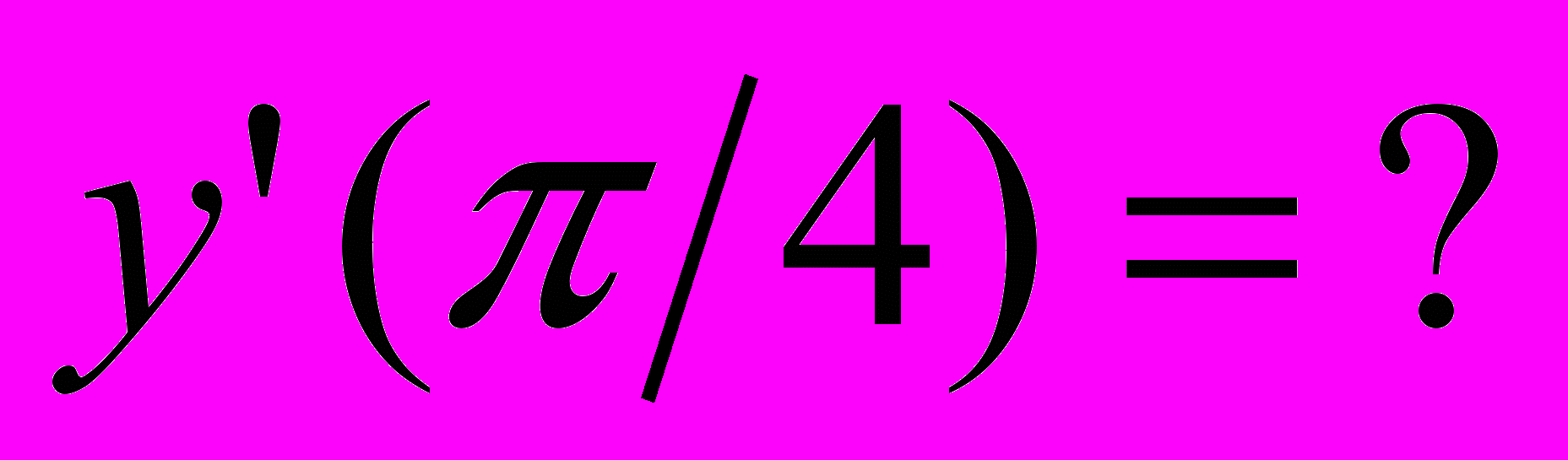
- Написать уравнение касательной к графику данной функции в точке
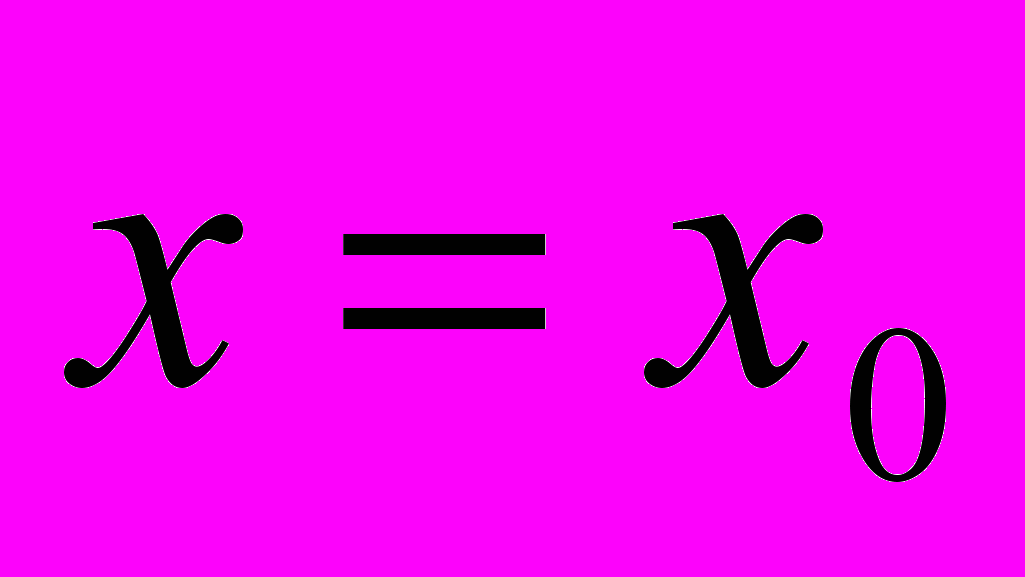
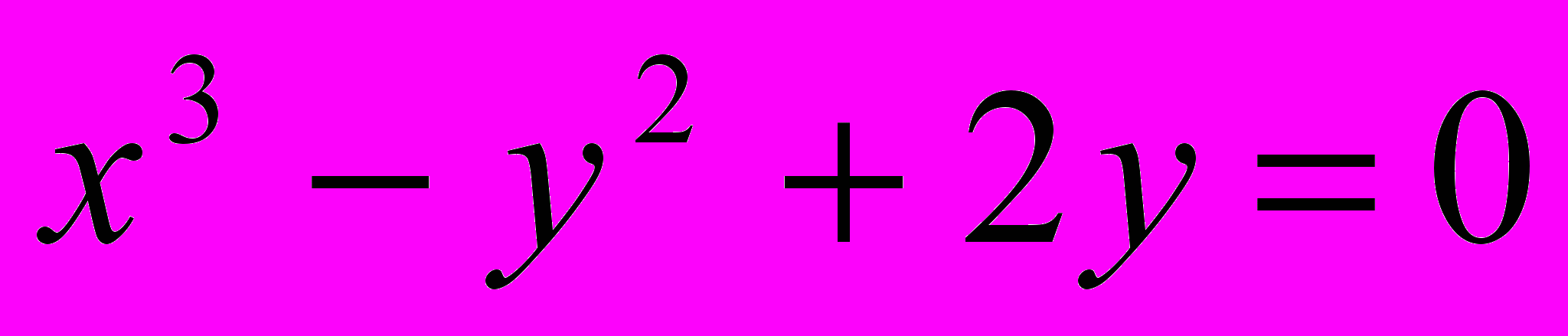 ,
, 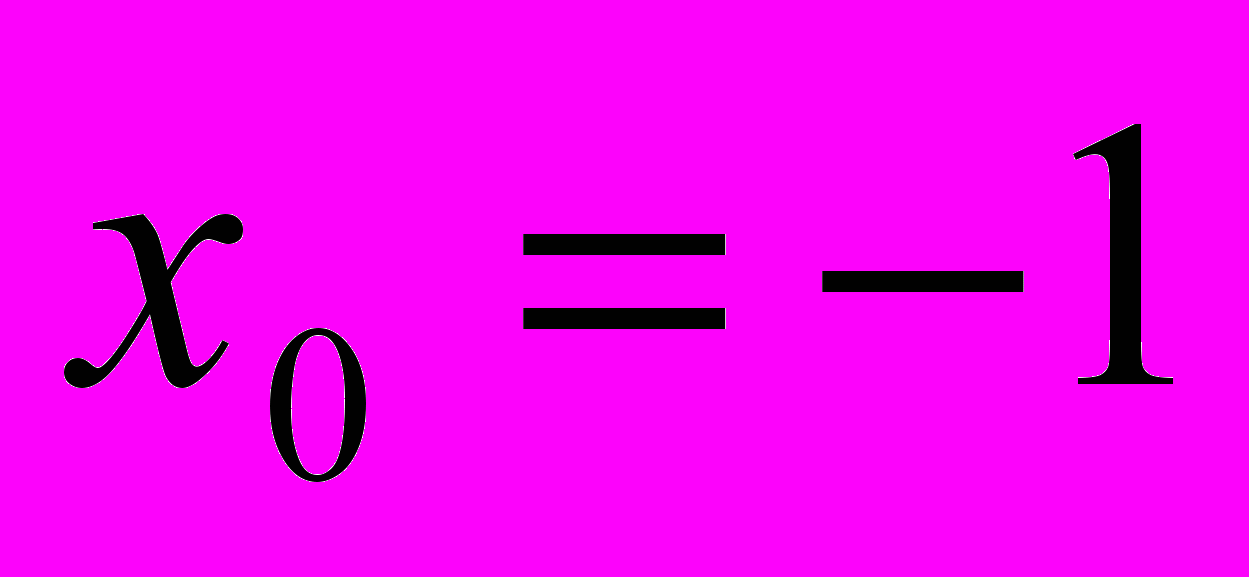
- Записать дифференциал данной функции и вычислить его в точке
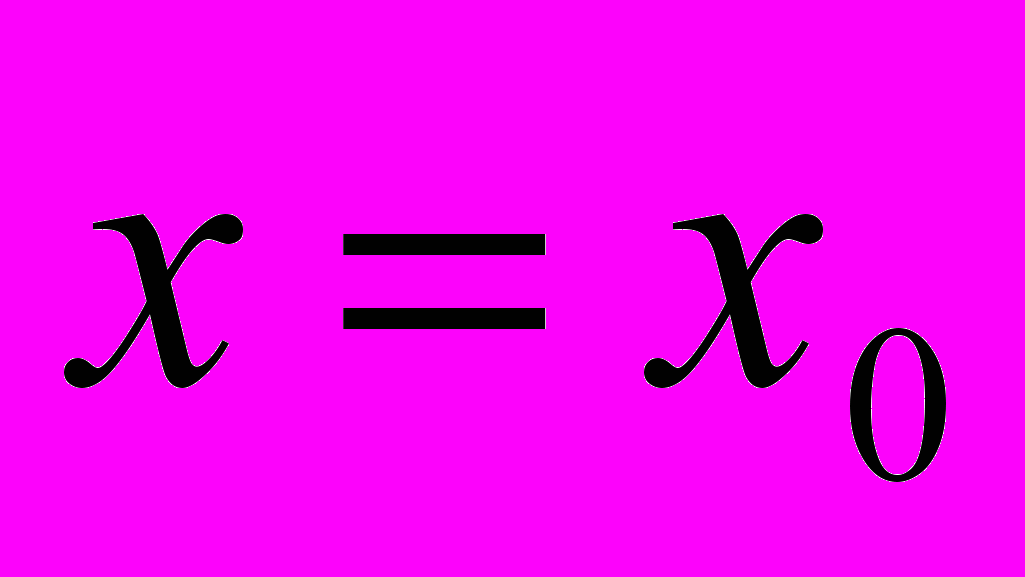 для
для 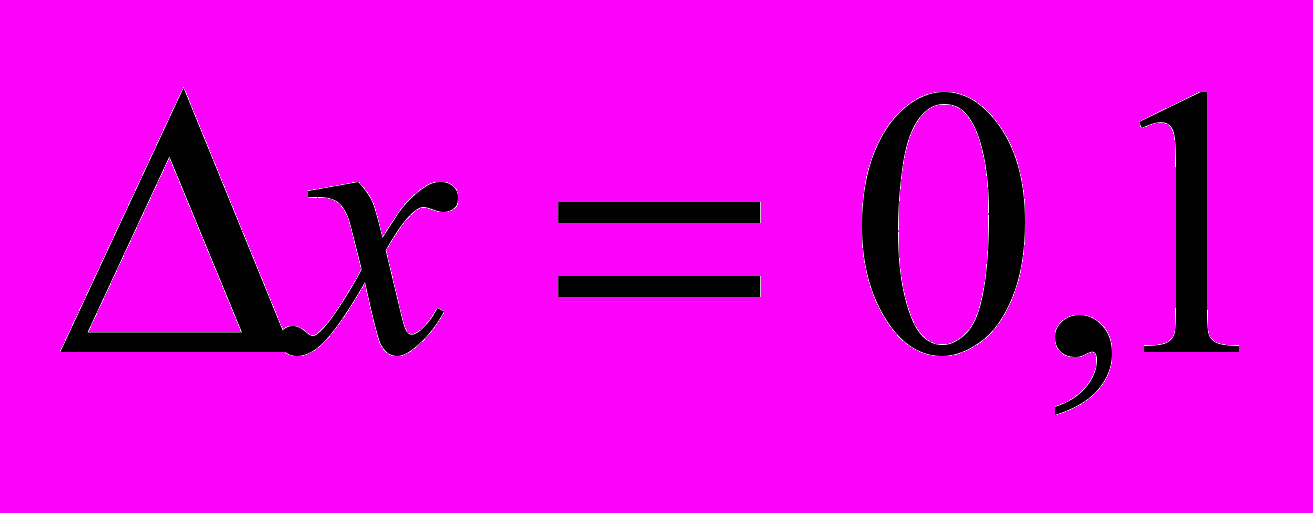
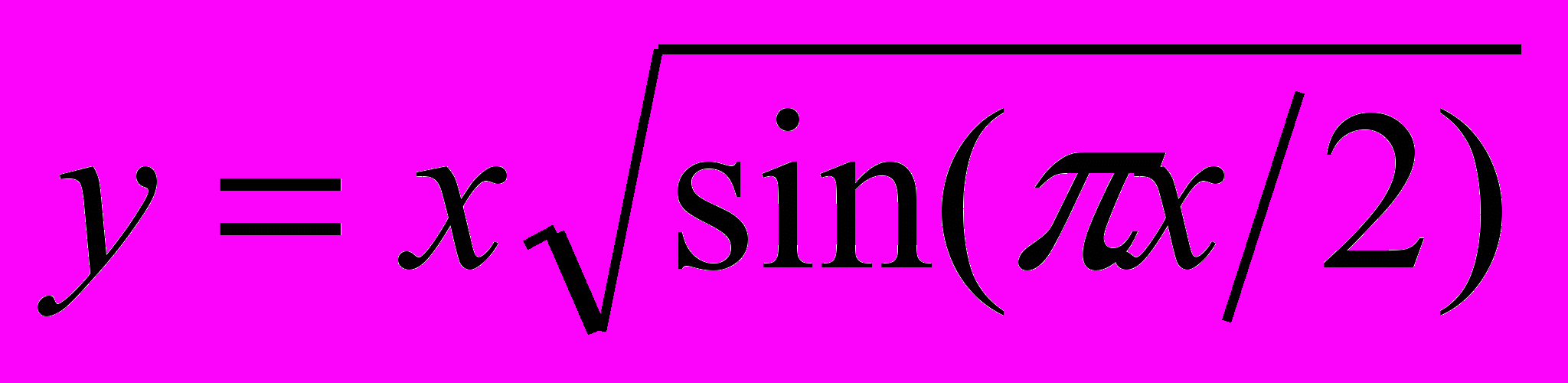 ,
, 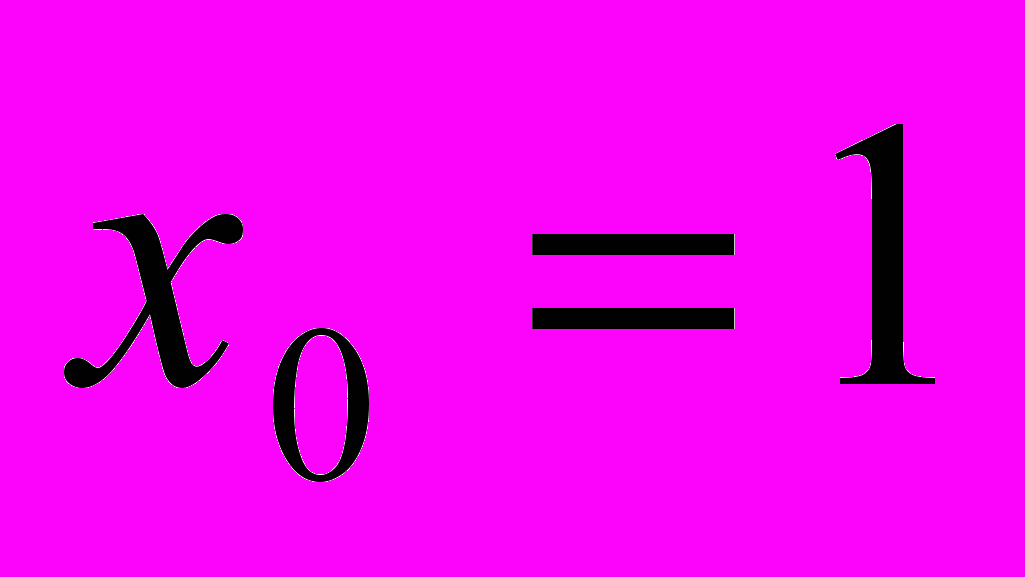
Контрольная работа № 3. Интегральное исчисление.
Пример задания.
- Найти неопределенный интеграл
1.1
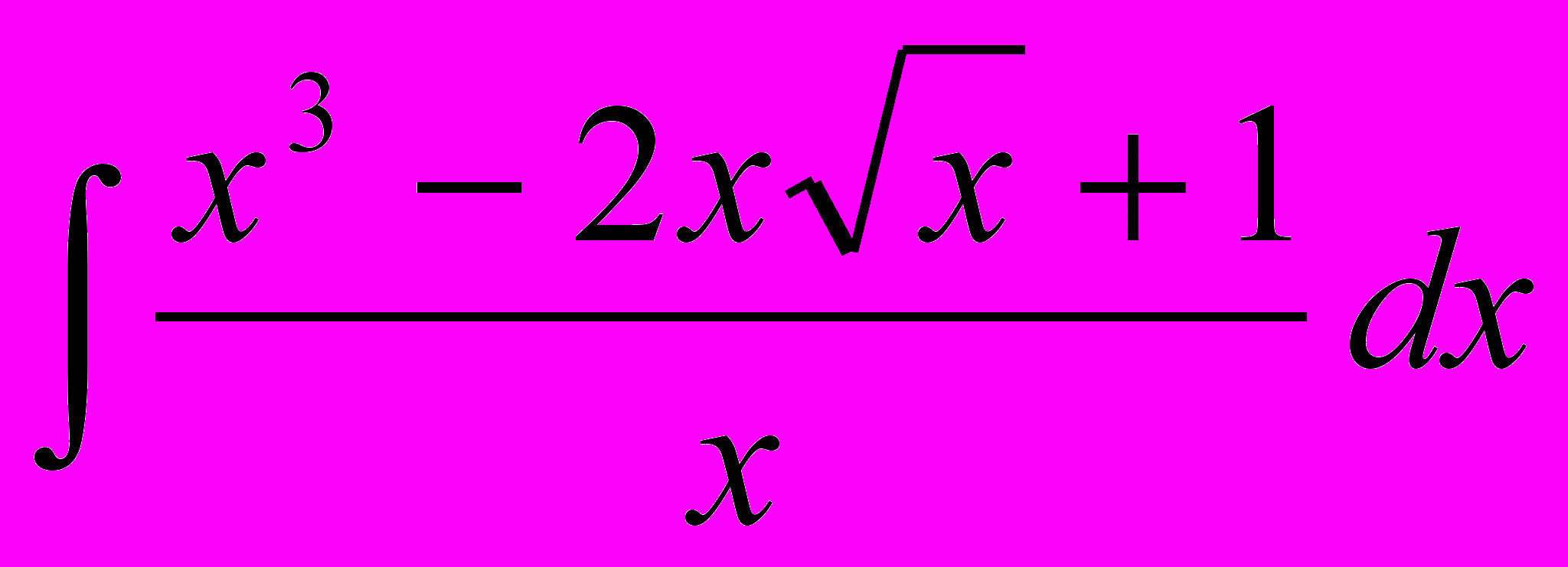
1.2
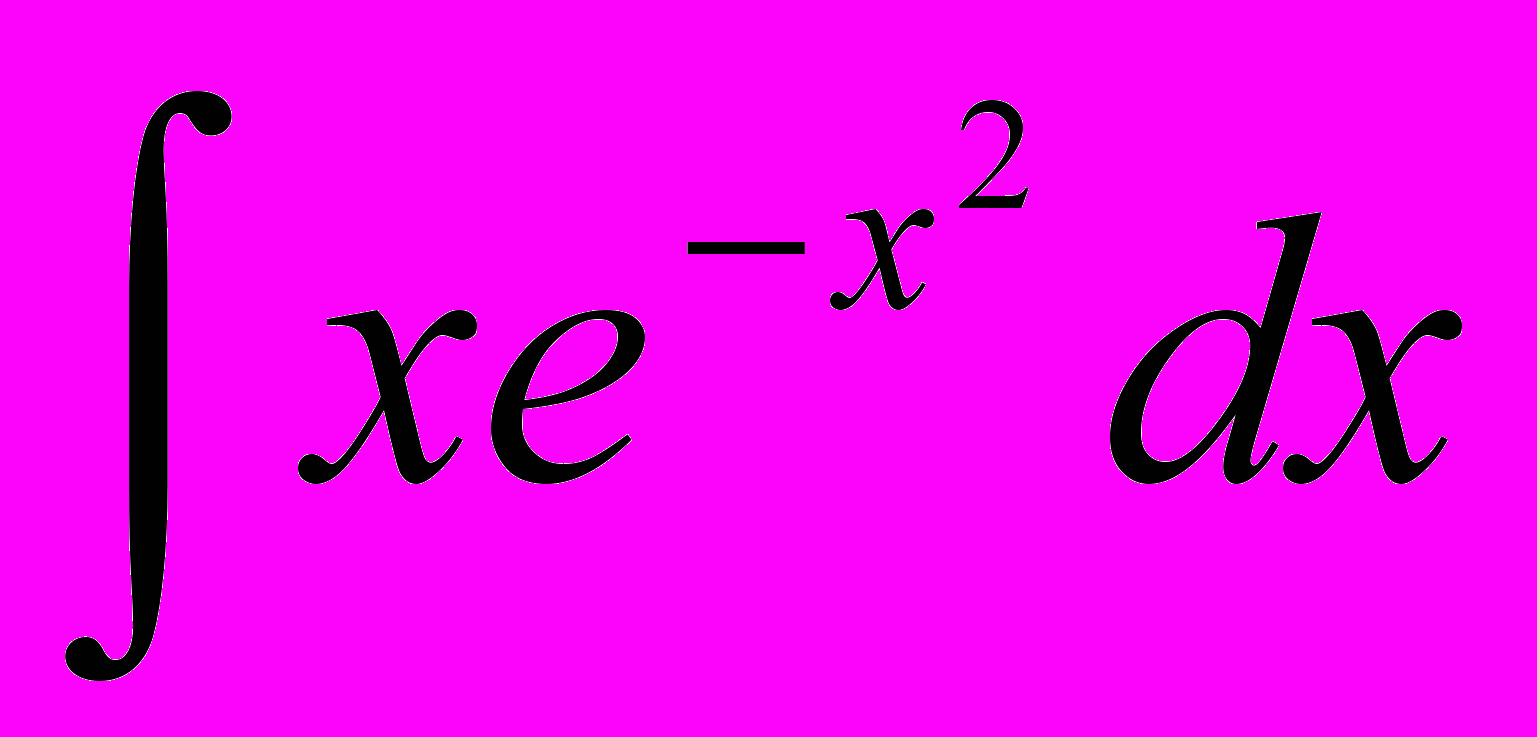
1.3
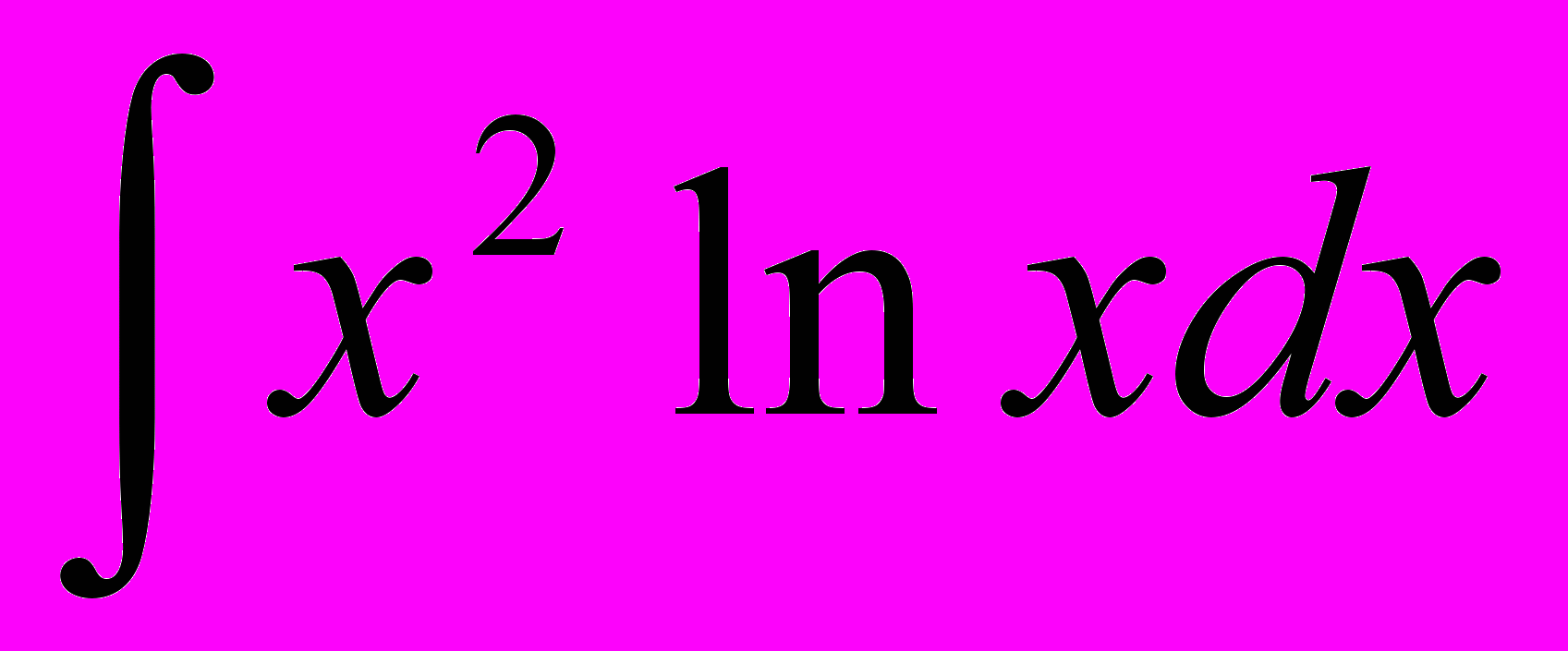
1.4
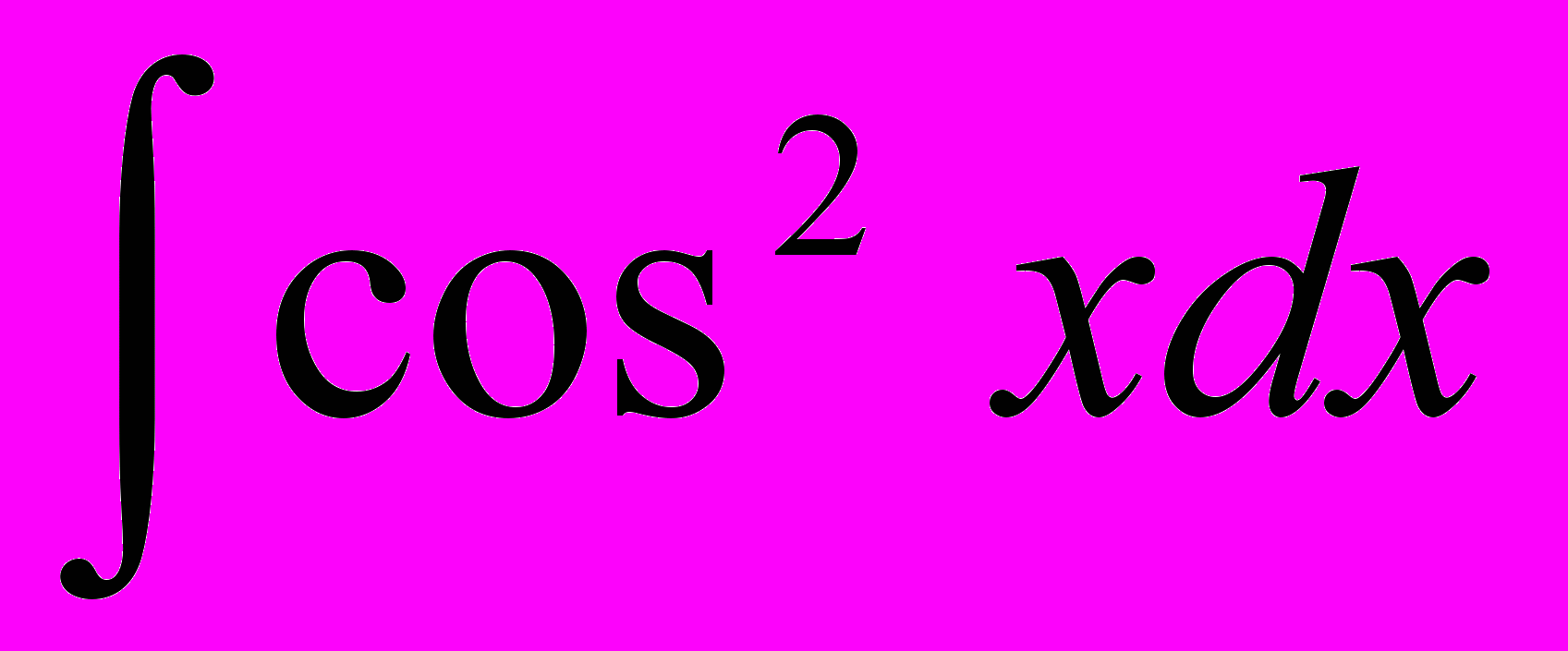
1. 5
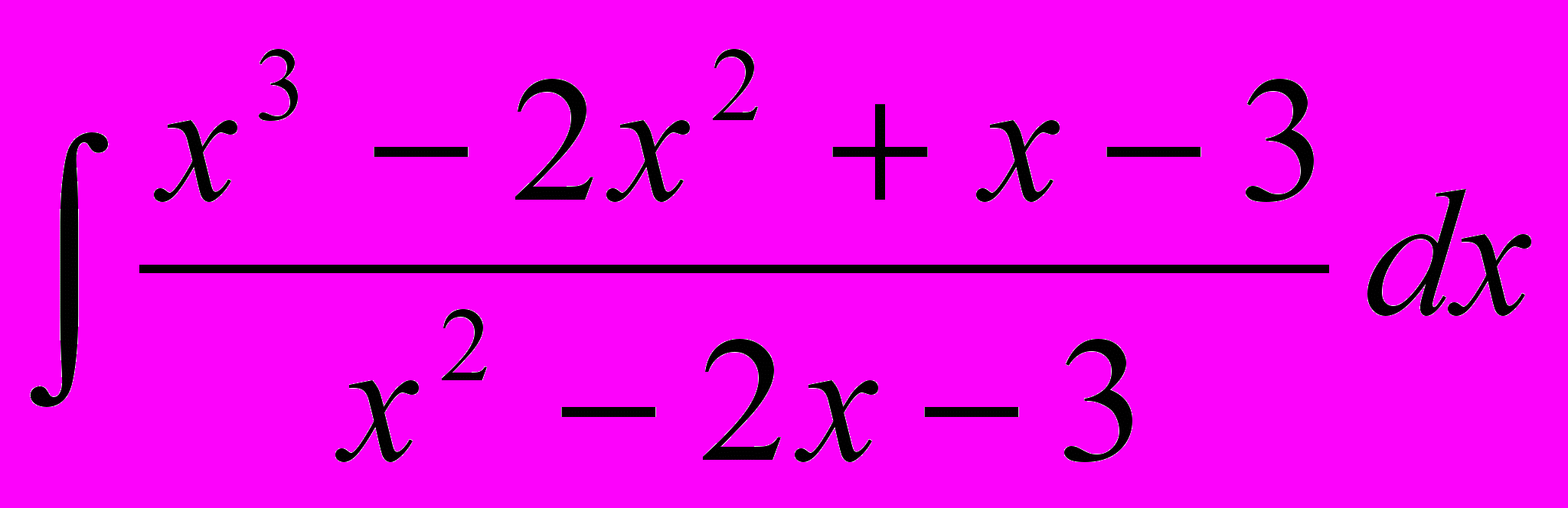
- Вычислить определенный интеграл
2.1
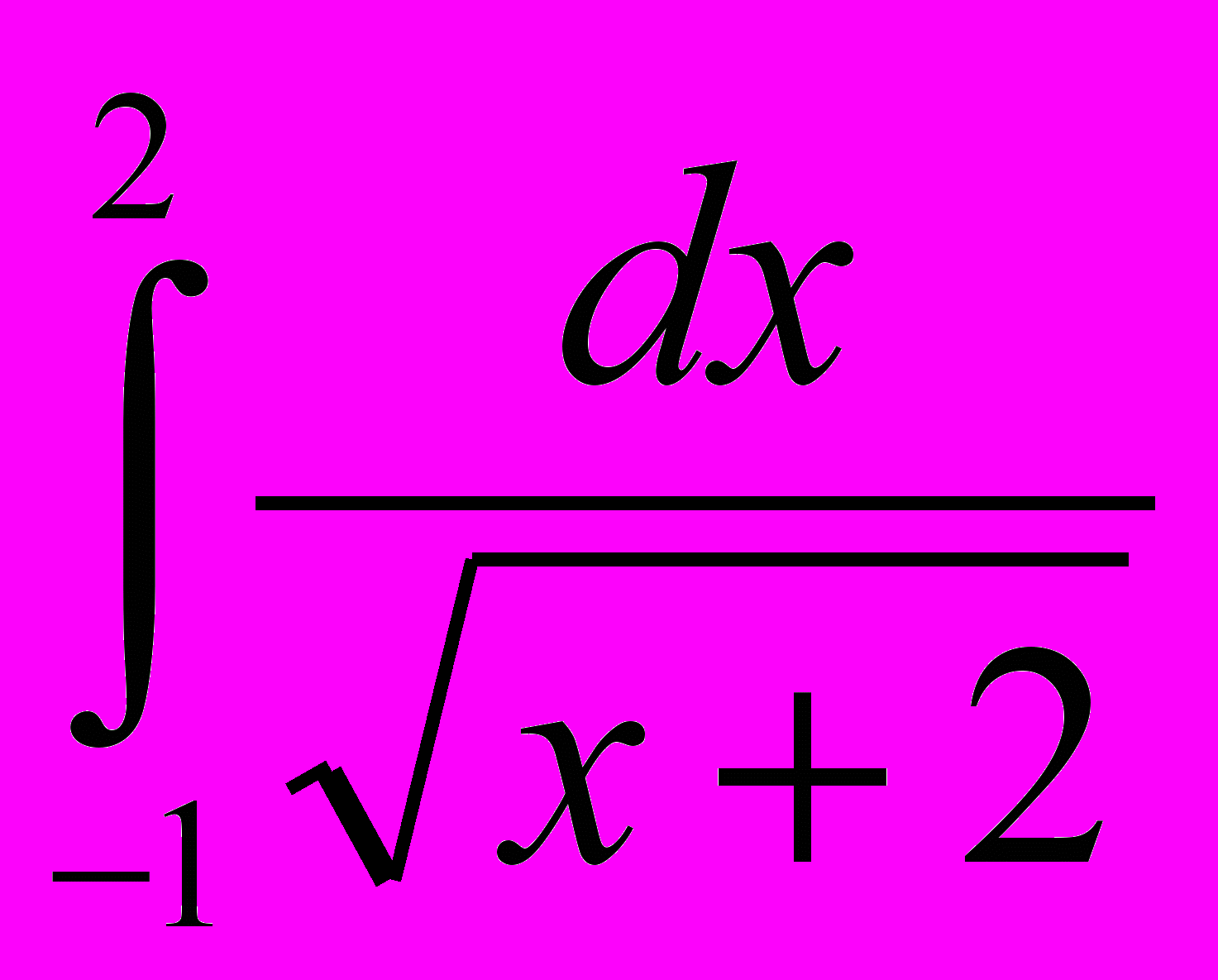
2.2
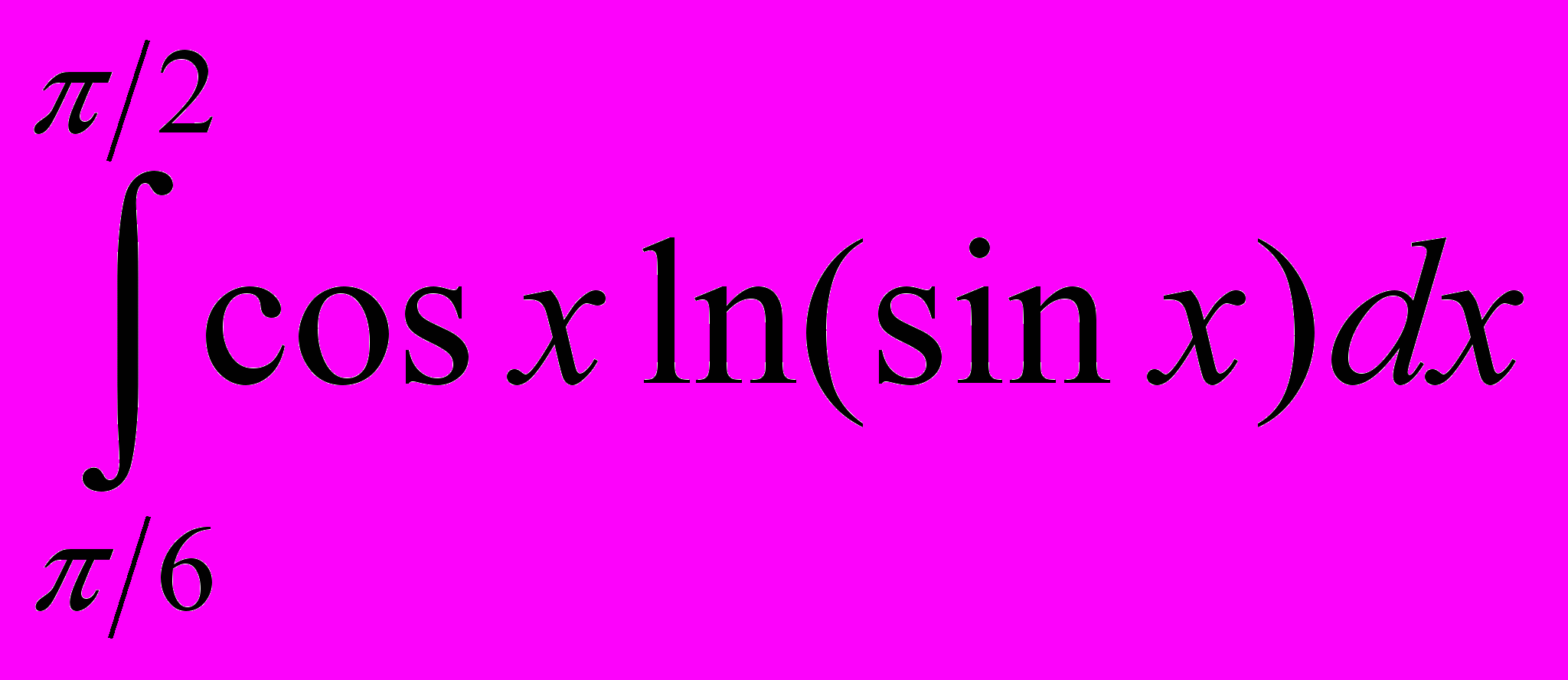
- Найти площадь криволинейной трапеции, ограниченной данными линиями
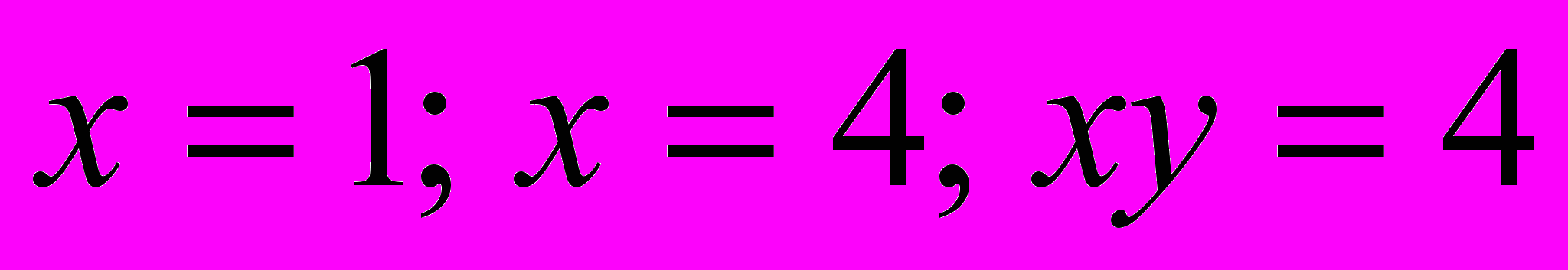
- Вычислить несобственные интегралы
4.1
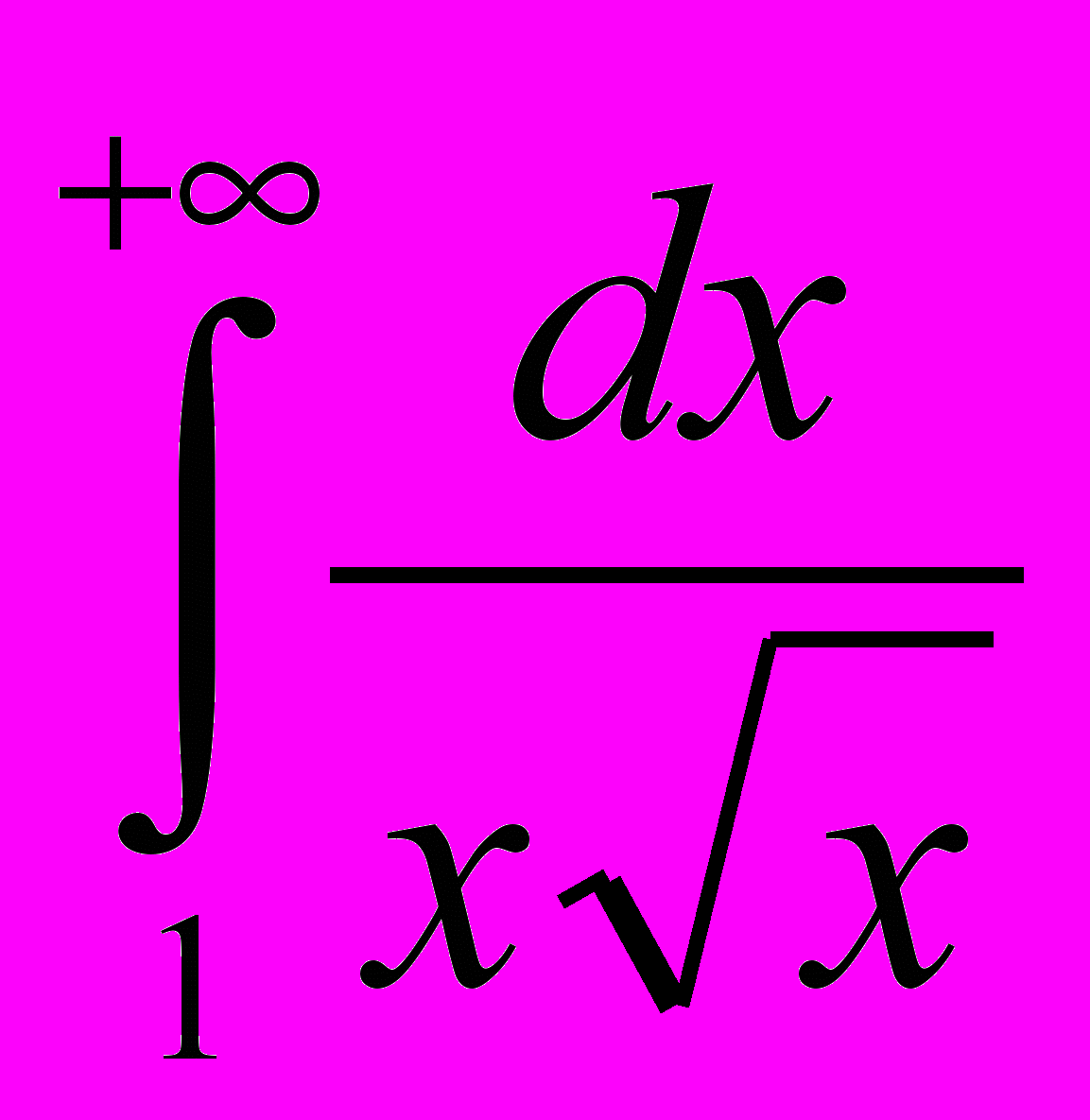
4.2
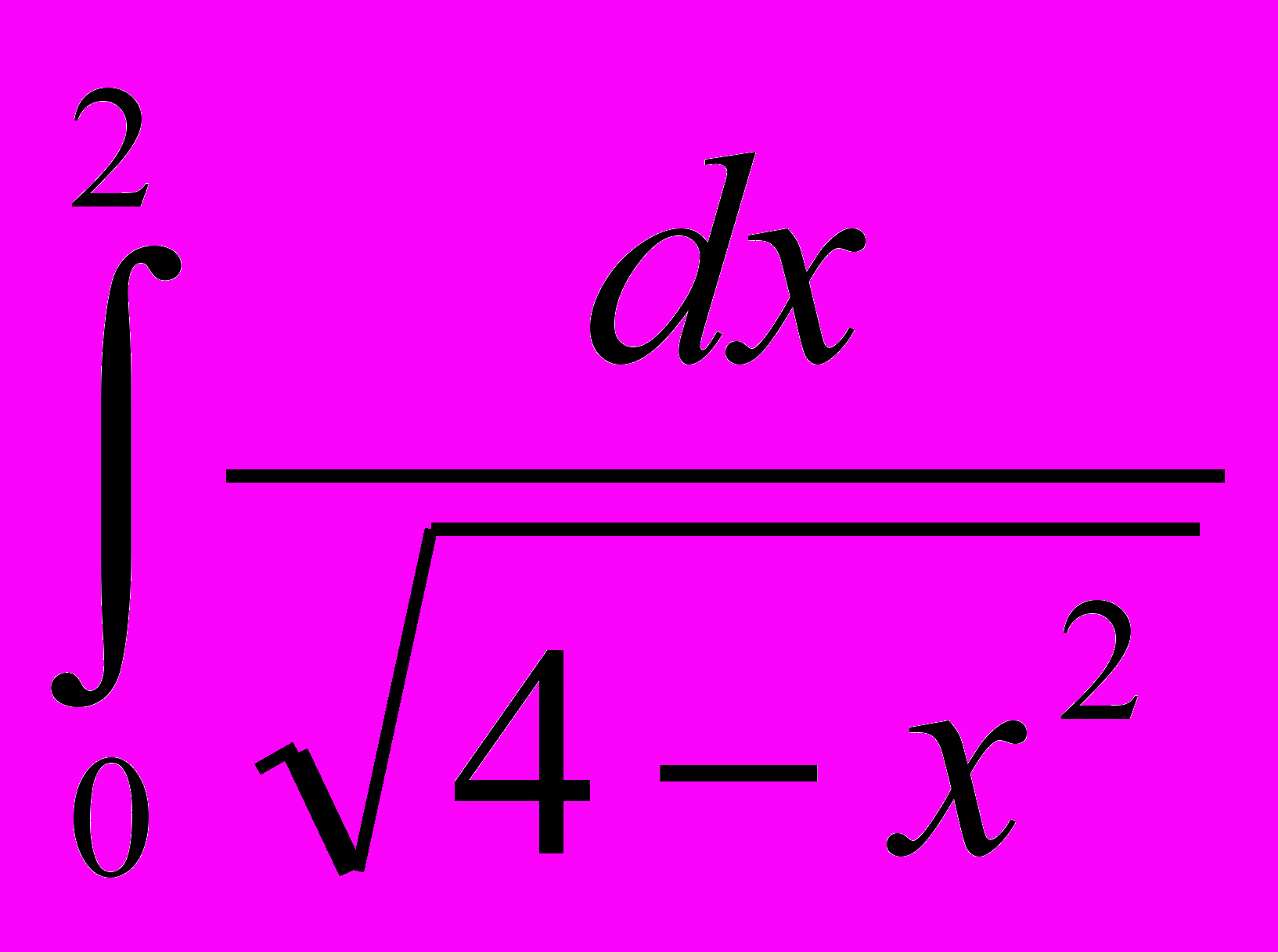
Контрольная работа №4. Дифференциальные уравнения
Пример задания.
- Найти общее решение (общий интеграл) дифференциального уравнения
1.1
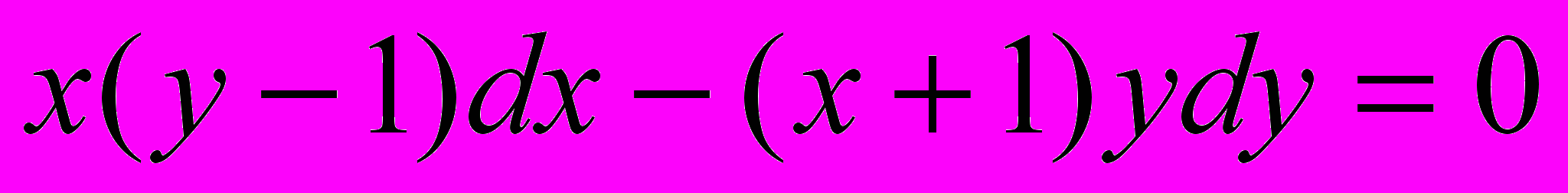
1.2
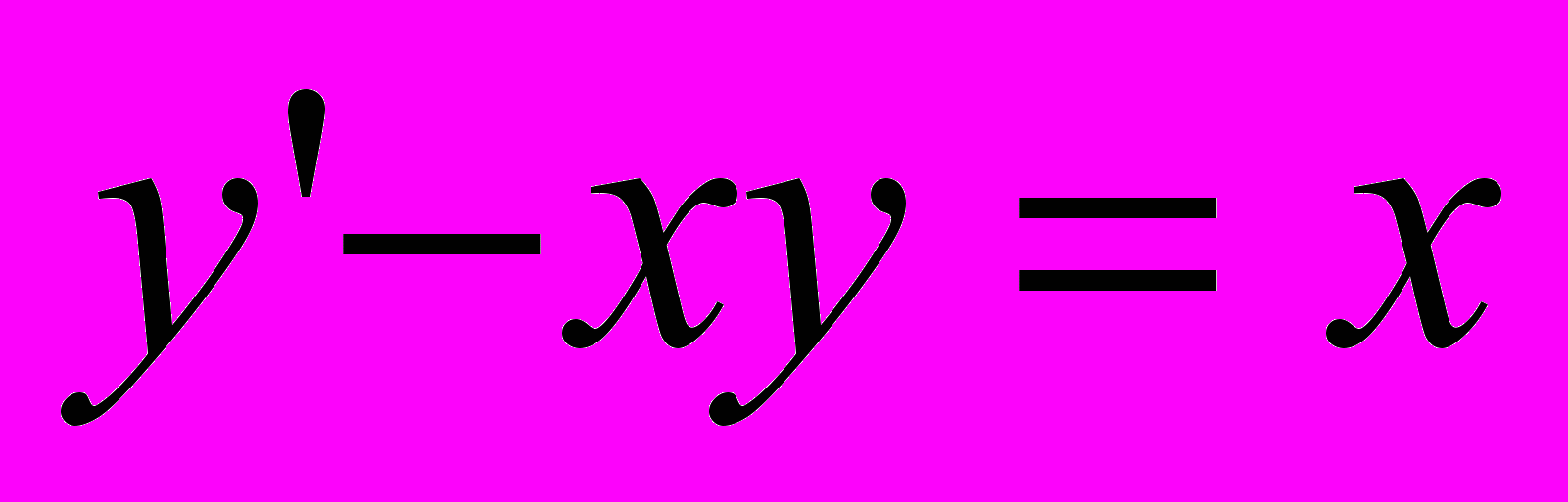
1.3
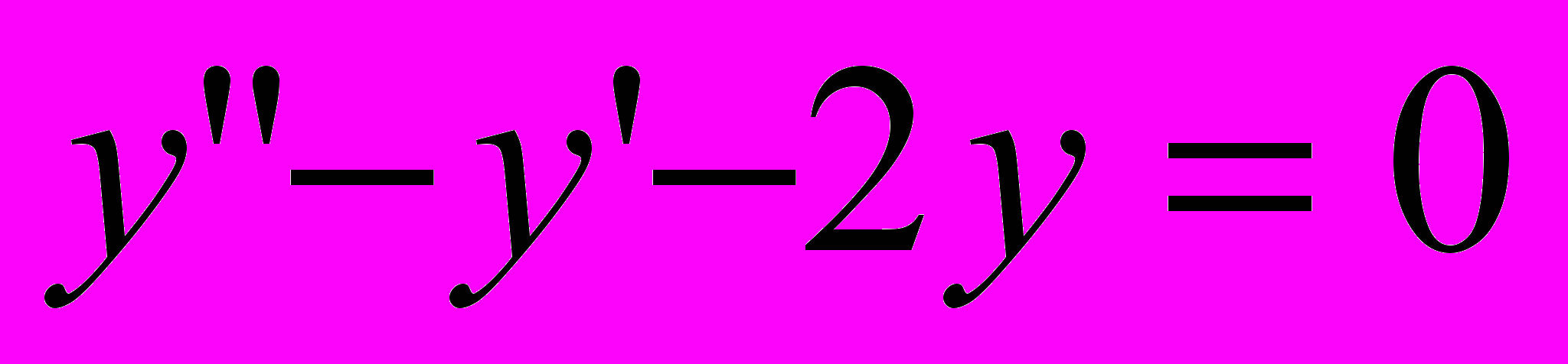
- Найти частное решение, удовлетворяющее данным начальным условиям
2.1
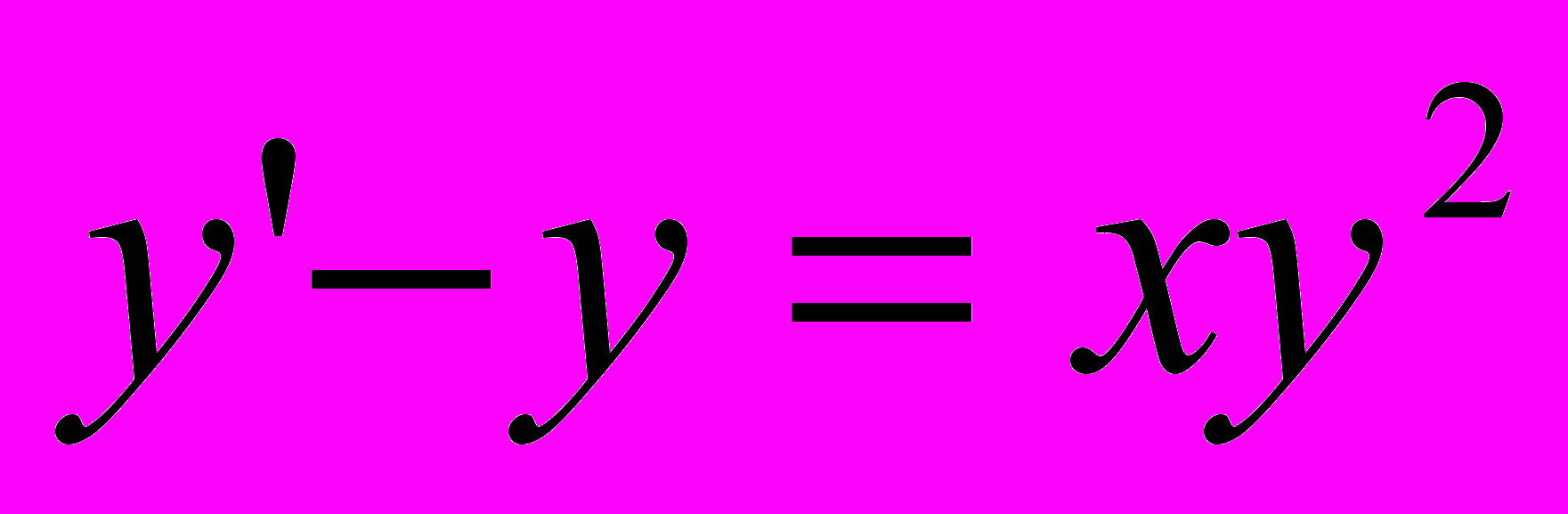 ,
, 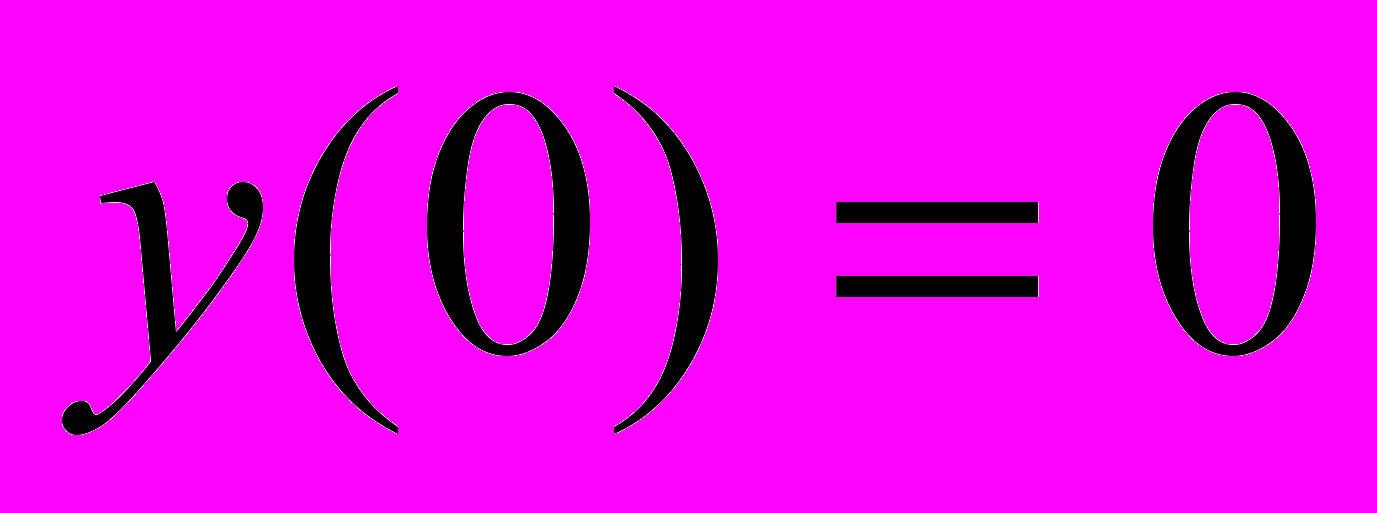
2.2
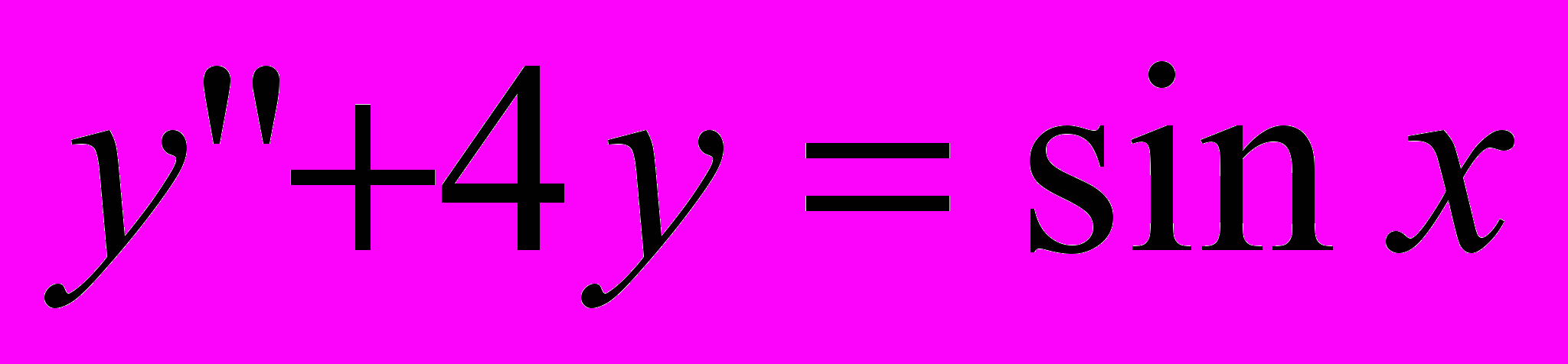 ,
, 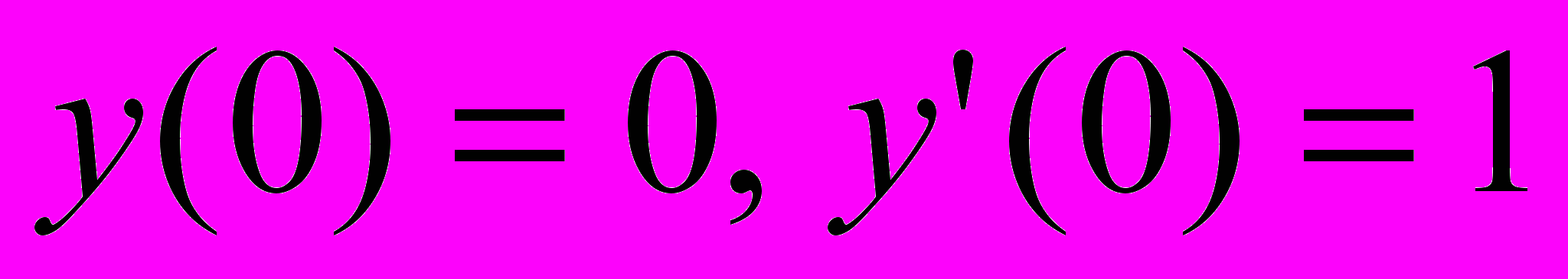
- Решить систему дифференциальных уравнений
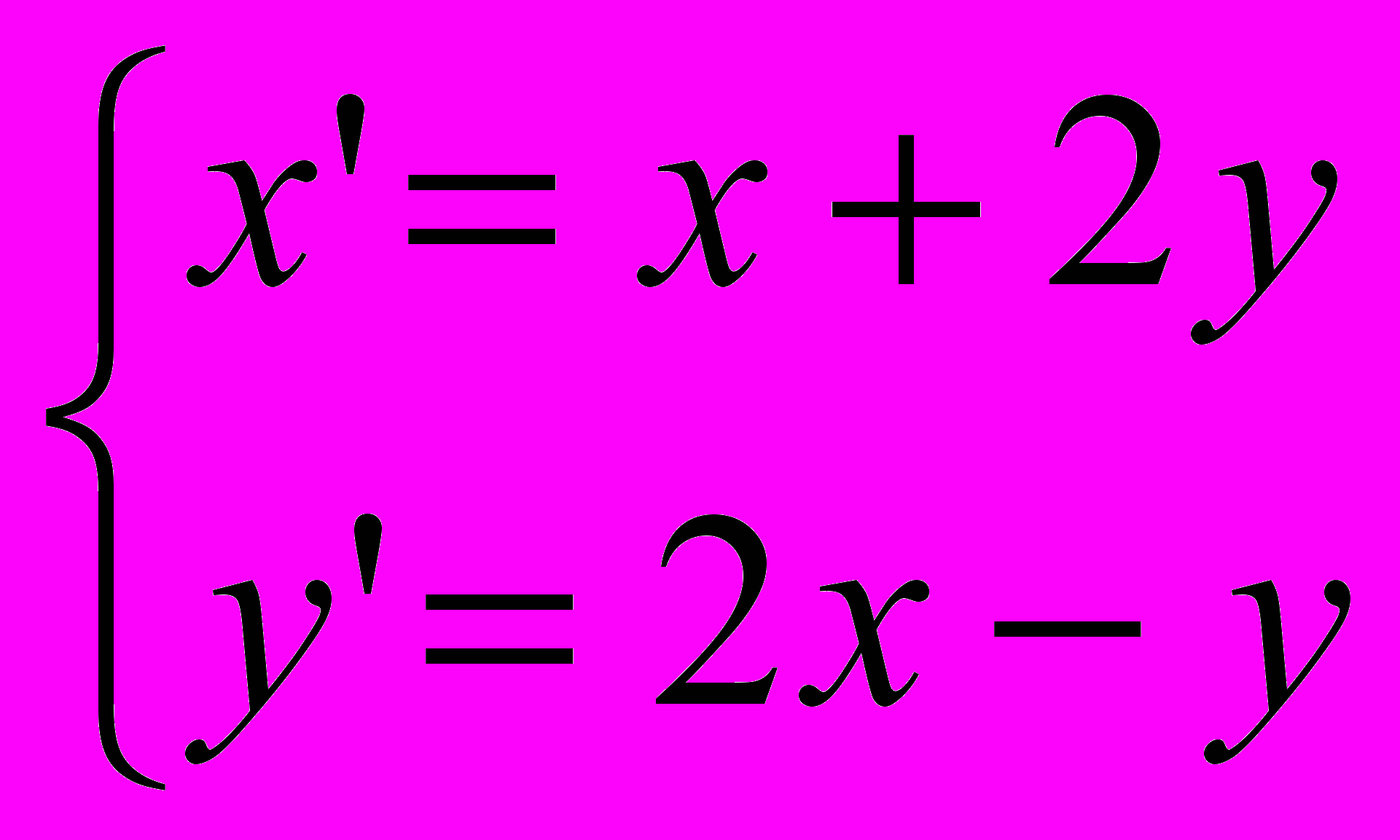
Для самостоятельной работы, при выполнении домашних работ, а также при подготовке к контрольным работам используются учебные материалы, приведенные ниже:
1. Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов.-13-е изд. - М.: Наука,1987.-360 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учебное пособие для втузов: В 2-х т. Т.1.Т.2.-Стереотип.изд. .-М: Интеграл-Пресс, 2000.-415с.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2 ч.: Учебное пособие для вузов./Данко П.Е., Попов А.Г., Кожевникова Т.Я.- 3-е изд., пераб. и доп. - М.: Высш. шк.,1980.-320 с.
4. Методические указания и варианты заданий для индивидуальной работы студентов по теме «Неопределенный и определенный интегралы (варианты 1-30)/ИГХТА; Сост. А.К. Ратыни, А.Н.Бумагина, Е.М.Михайлов.-Иваново,1996. -38с.№670
5.Методические указания и варианты заданий для индивидуальной работы студентов по теме «Неопределенный и определенный интегралы (варианты 31-60)/ИГХТА; Сост. А.К.Ратыни, А.Н.Бумагина, Е.М.Михайлов.- Иваново, 1998.-40с.№708
Контрольно-измерительные материалы для итогового контроля
Итоговый экзамен по дисциплине проводится в виде письменного экзамена. Экзаменационный билет содержит 6 тестовых заданий и 4 задачи. Правильный ответ на каждое тестовое задание оценивается в 3 балла, решение каждой задачи оценивается из 8 баллов.
При оценке решения задачи письменного этапа экзамена учитывается правильность и полнота решения, правильность выбора метода решения, наличие необходимых пояснений, присутствие (если необходимо) графических иллюстраций, аккуратность оформления.
Пример экзаменационного билета.
Тестовые задания
| Вопрос | Ответы |
| 1. Функция 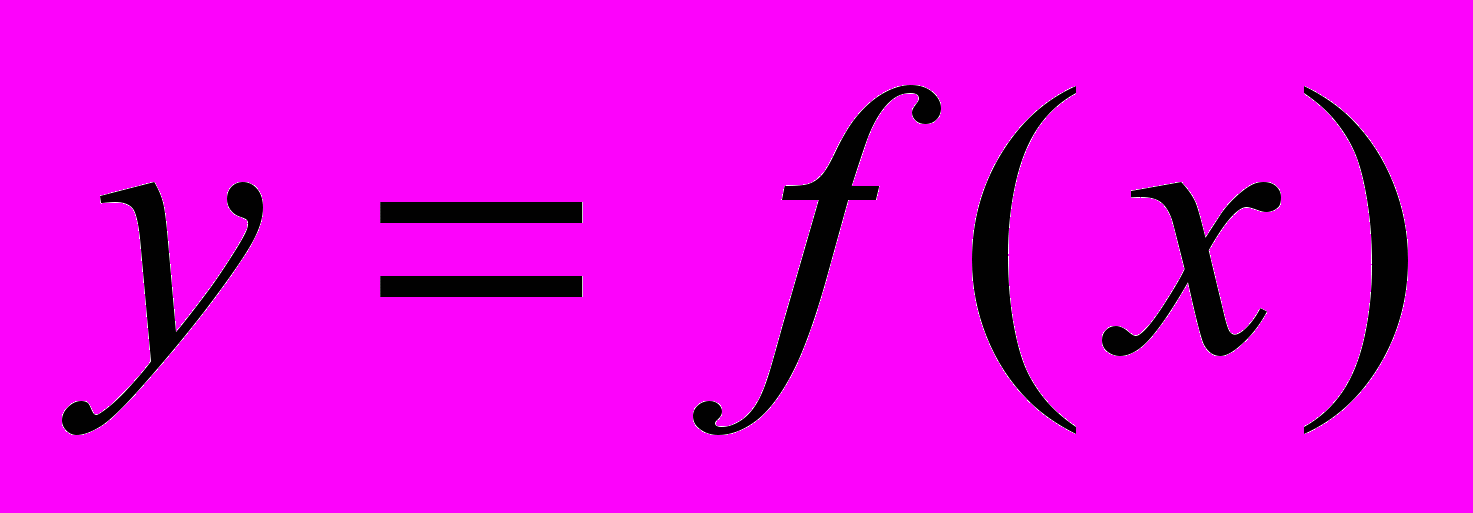 непрерывна в точке непрерывна в точке 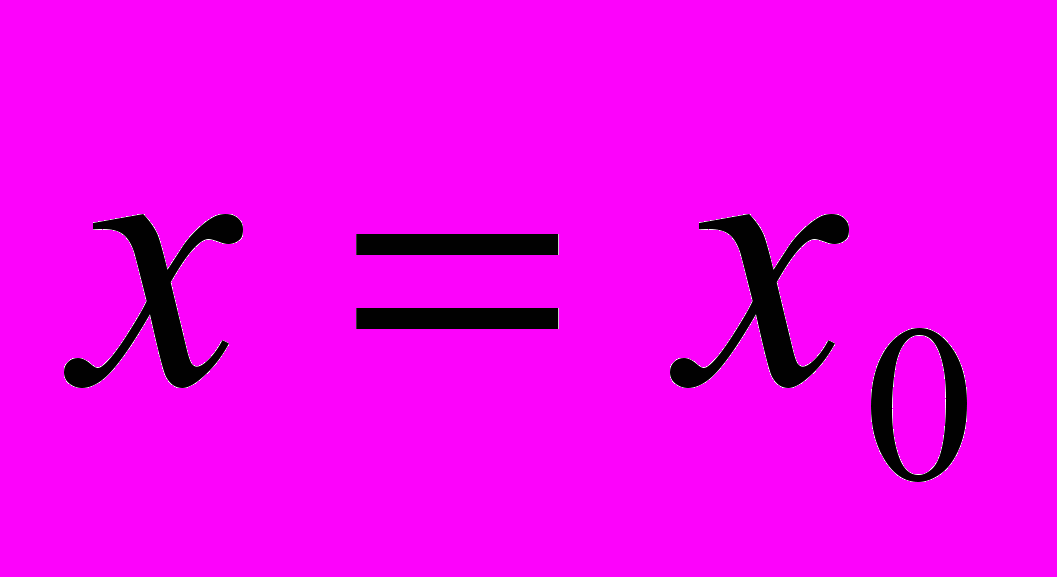 , если , еслиa. 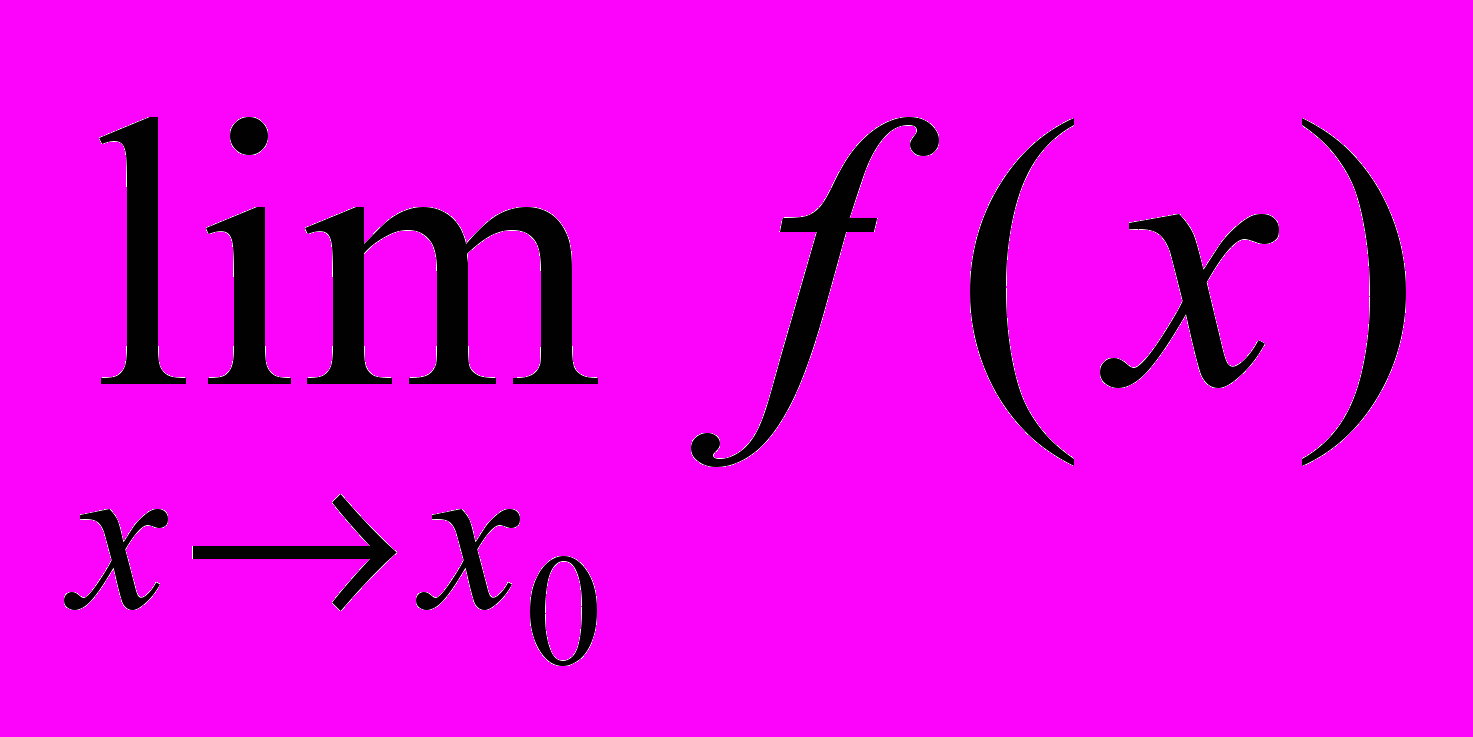 существует и конечен существует и конеченb. 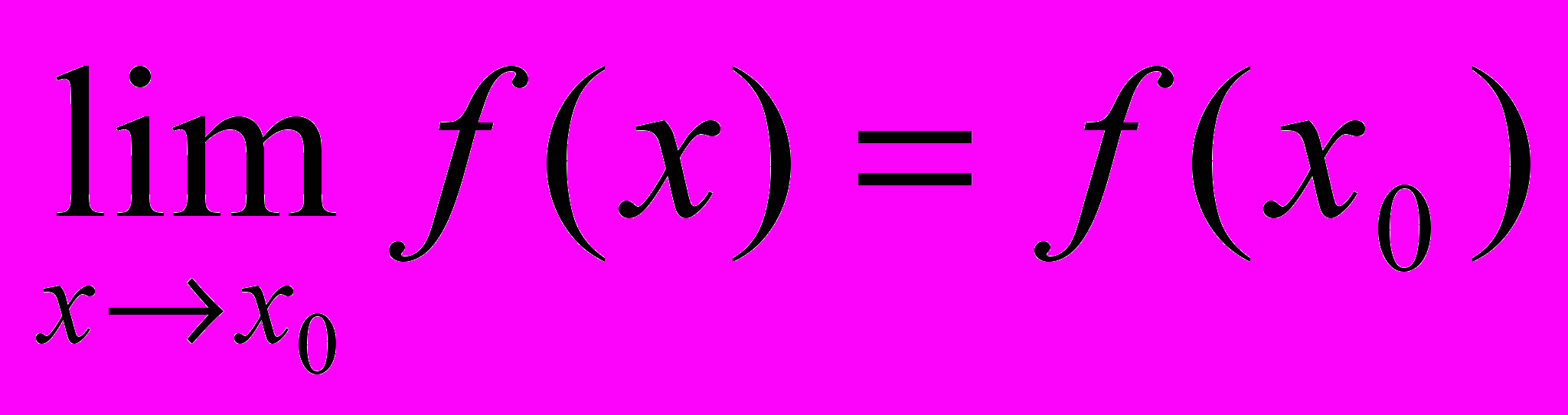 c. 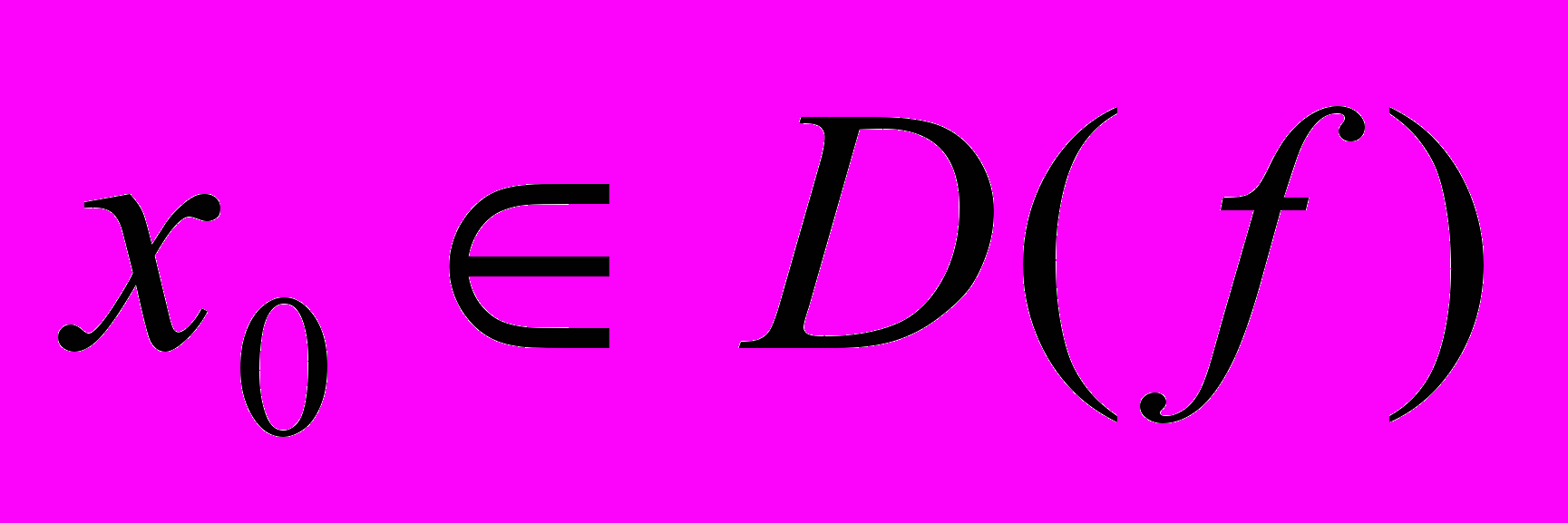 d. существует последовательность 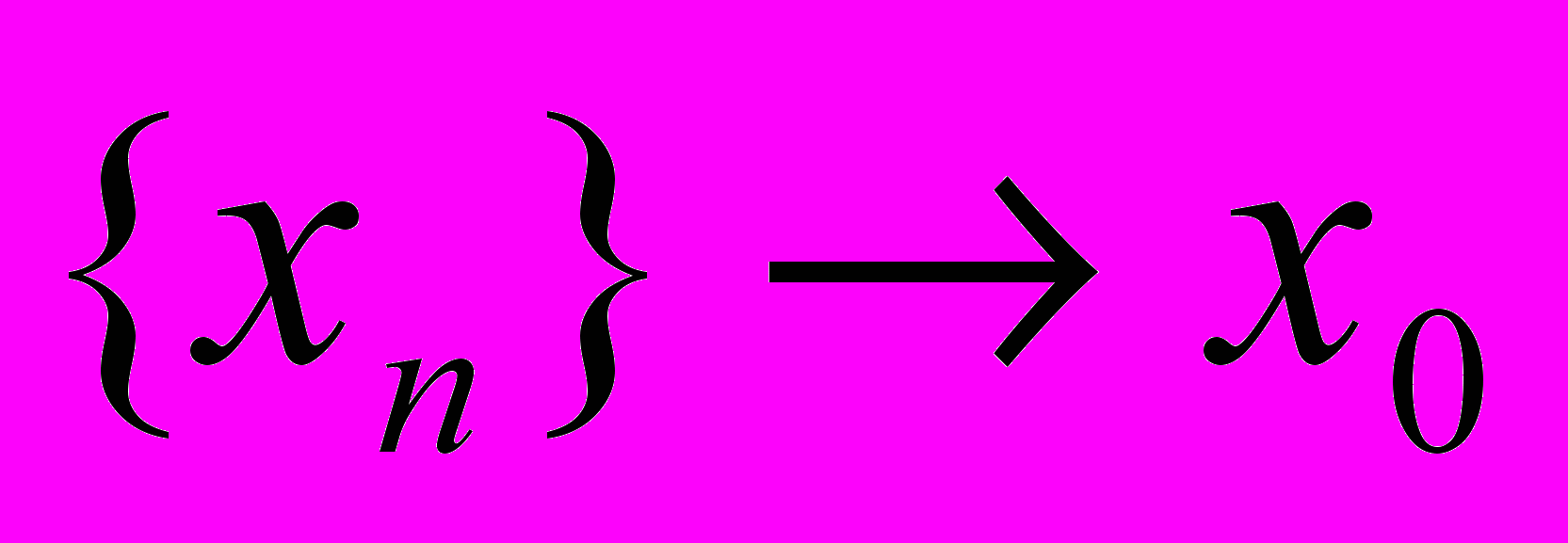 , для которой , для которой 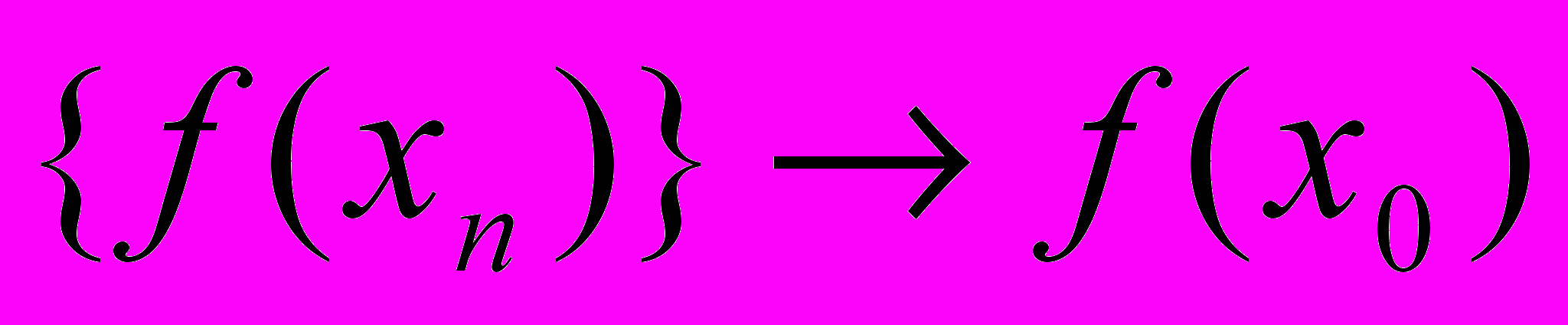 . .Указать правильный ответ | 1. a 2. b 3. c 4. d |
| 2. Дана функция 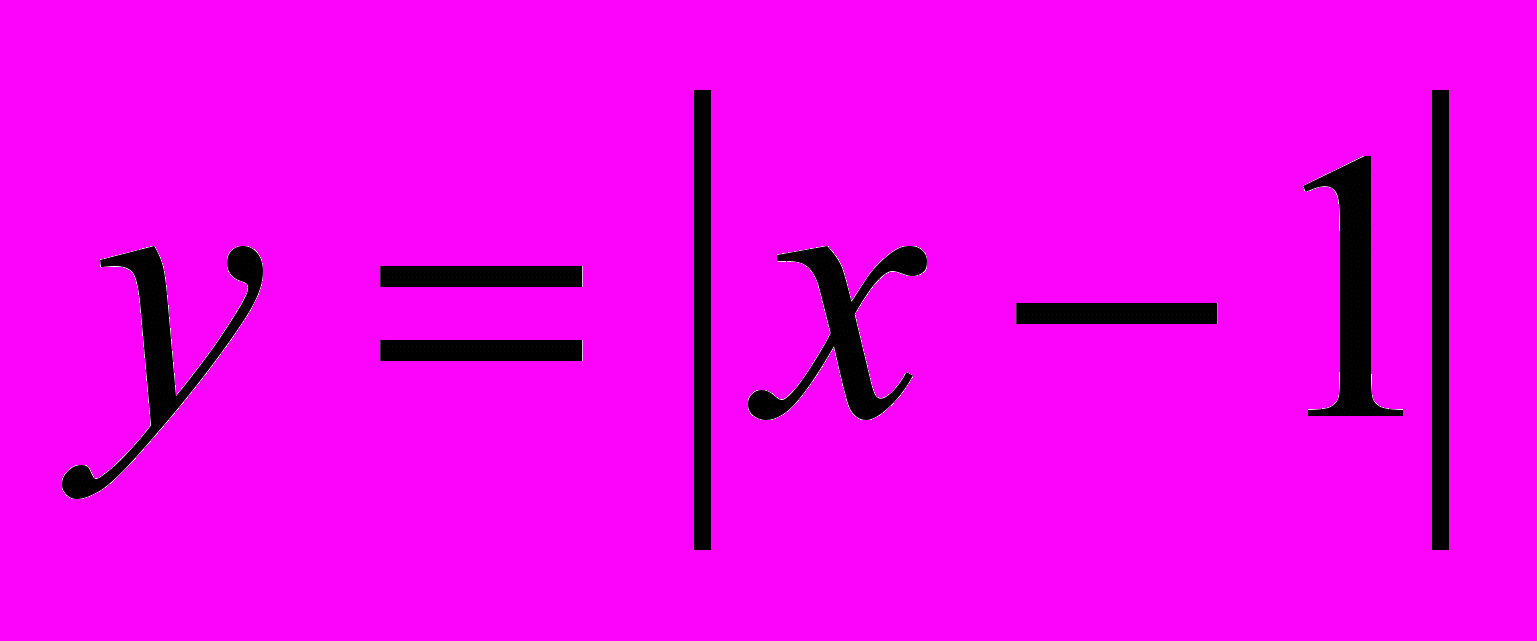 . Какое утверждение относительно касательной к графику этой функции в точке А(1;0) верно? . Какое утверждение относительно касательной к графику этой функции в точке А(1;0) верно? | 1.Ось Ох является касательной 2. Прямая 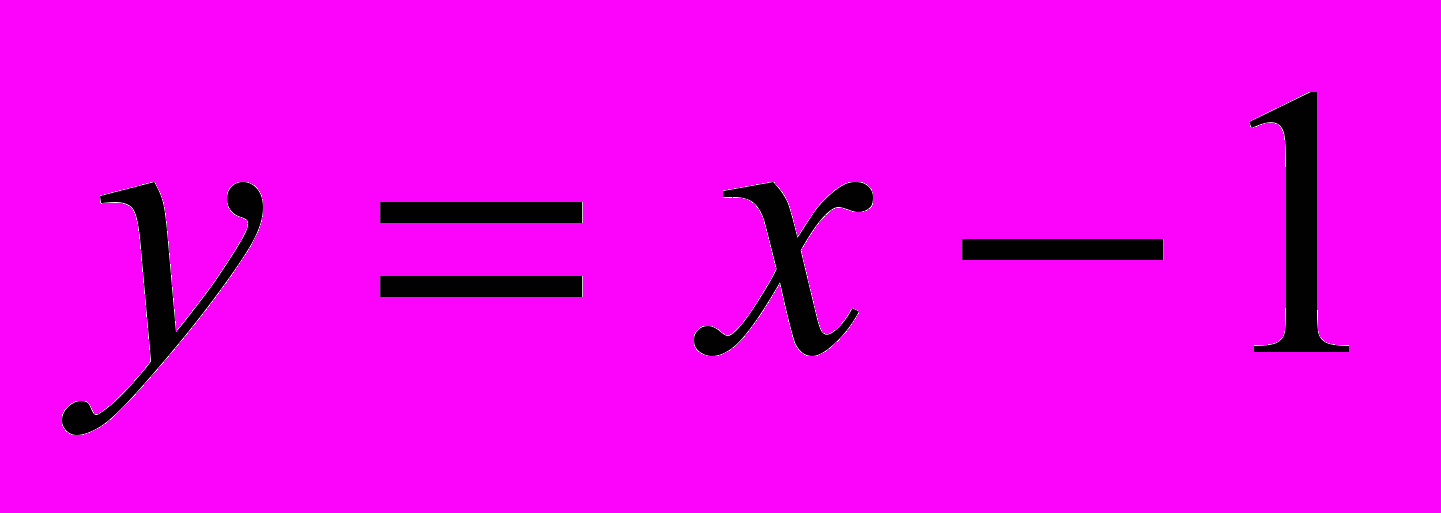 является касательной является касательной3. Любая прямая проходящая через точку А является касательной 4. Касательных в точке А нет. |
| 3. Пусть 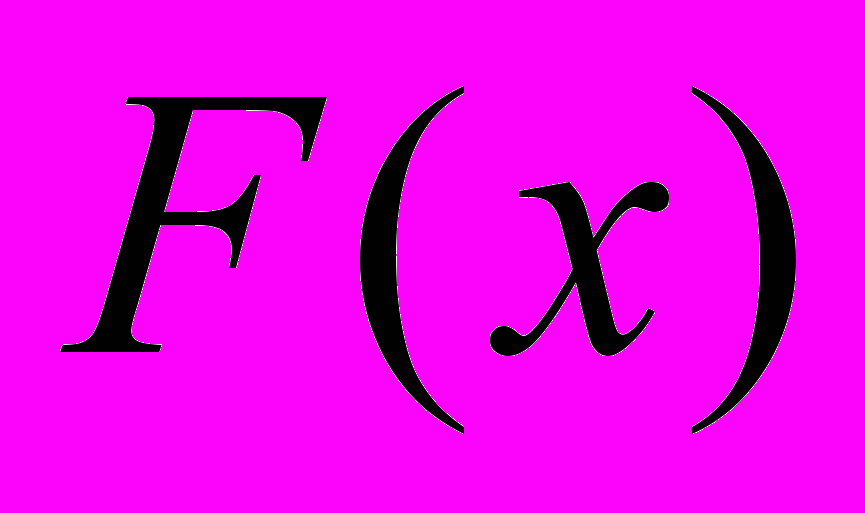 - какая-либо первообразная для - какая-либо первообразная для 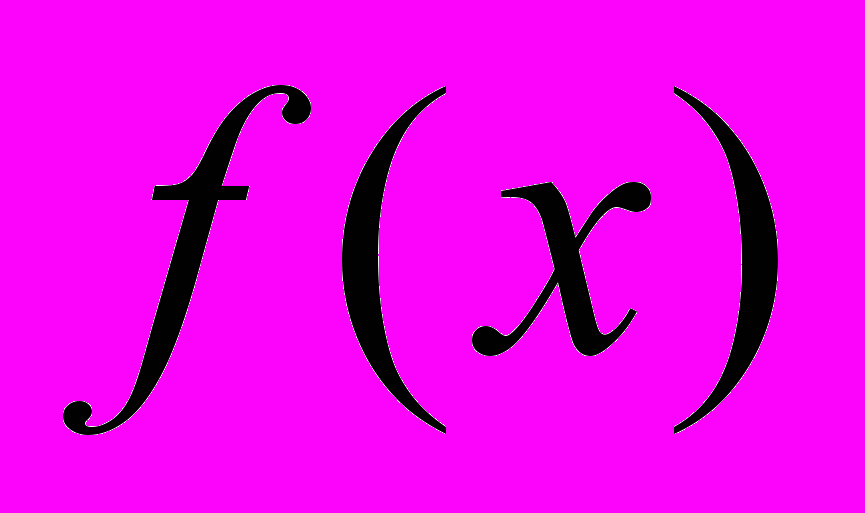 . Какая из приведенных функций является первообразной для . Какая из приведенных функций является первообразной для 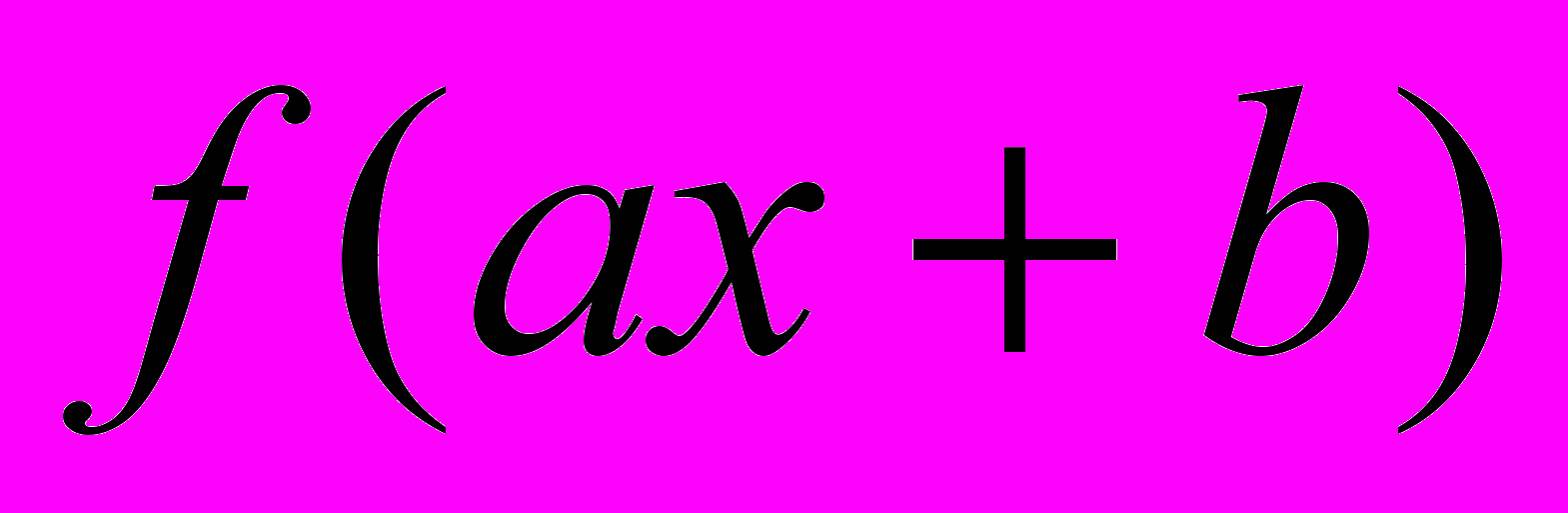 ? ? | 1. 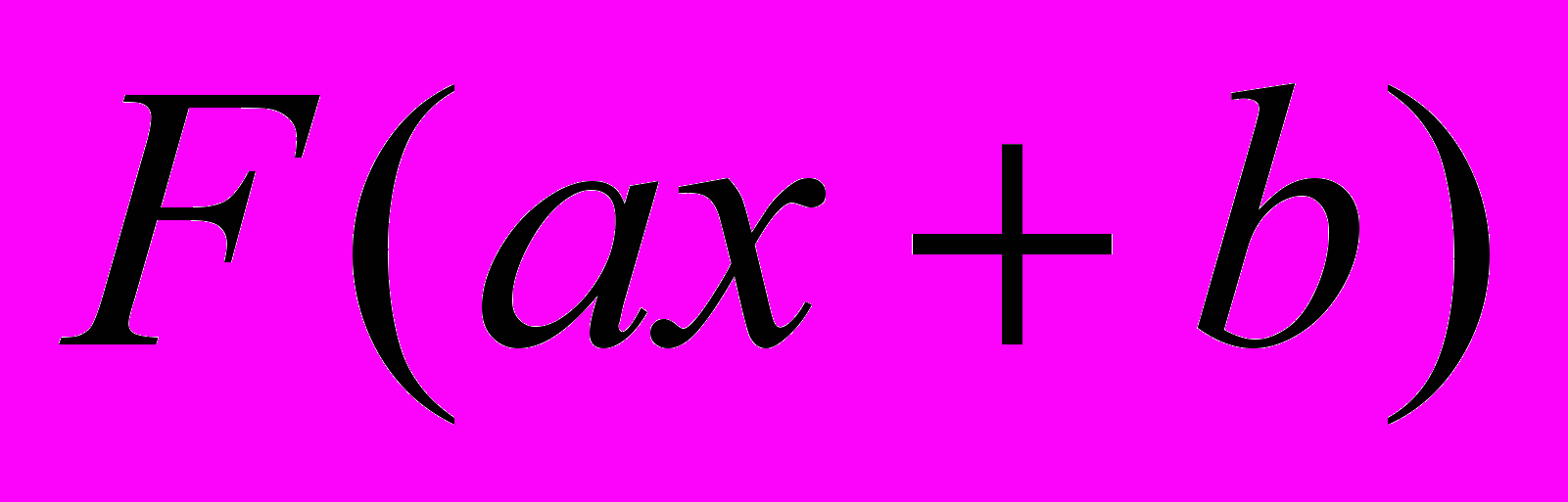 2. 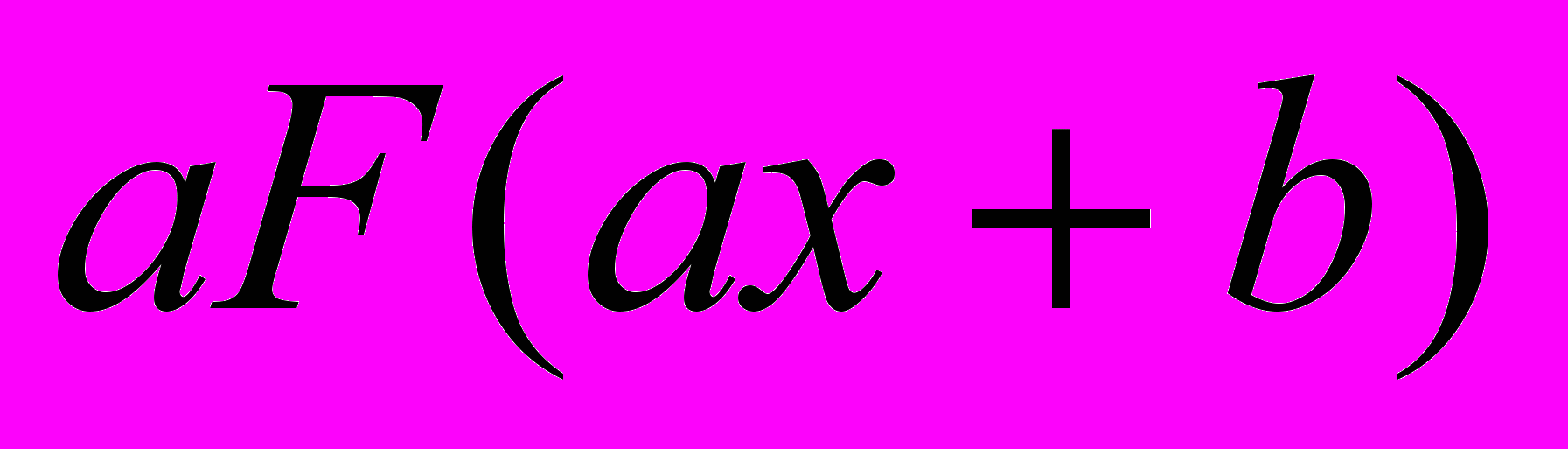 3. 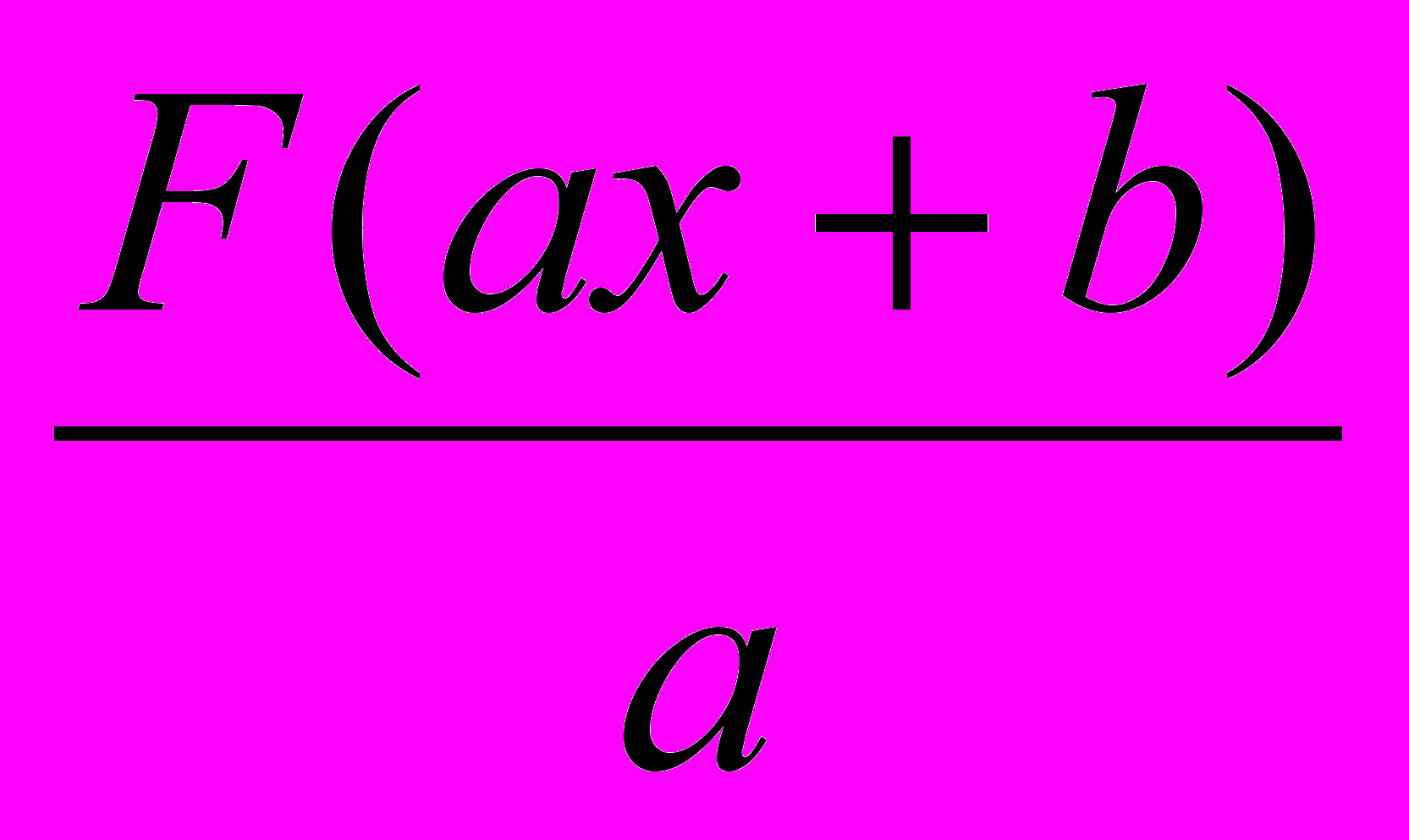 4. 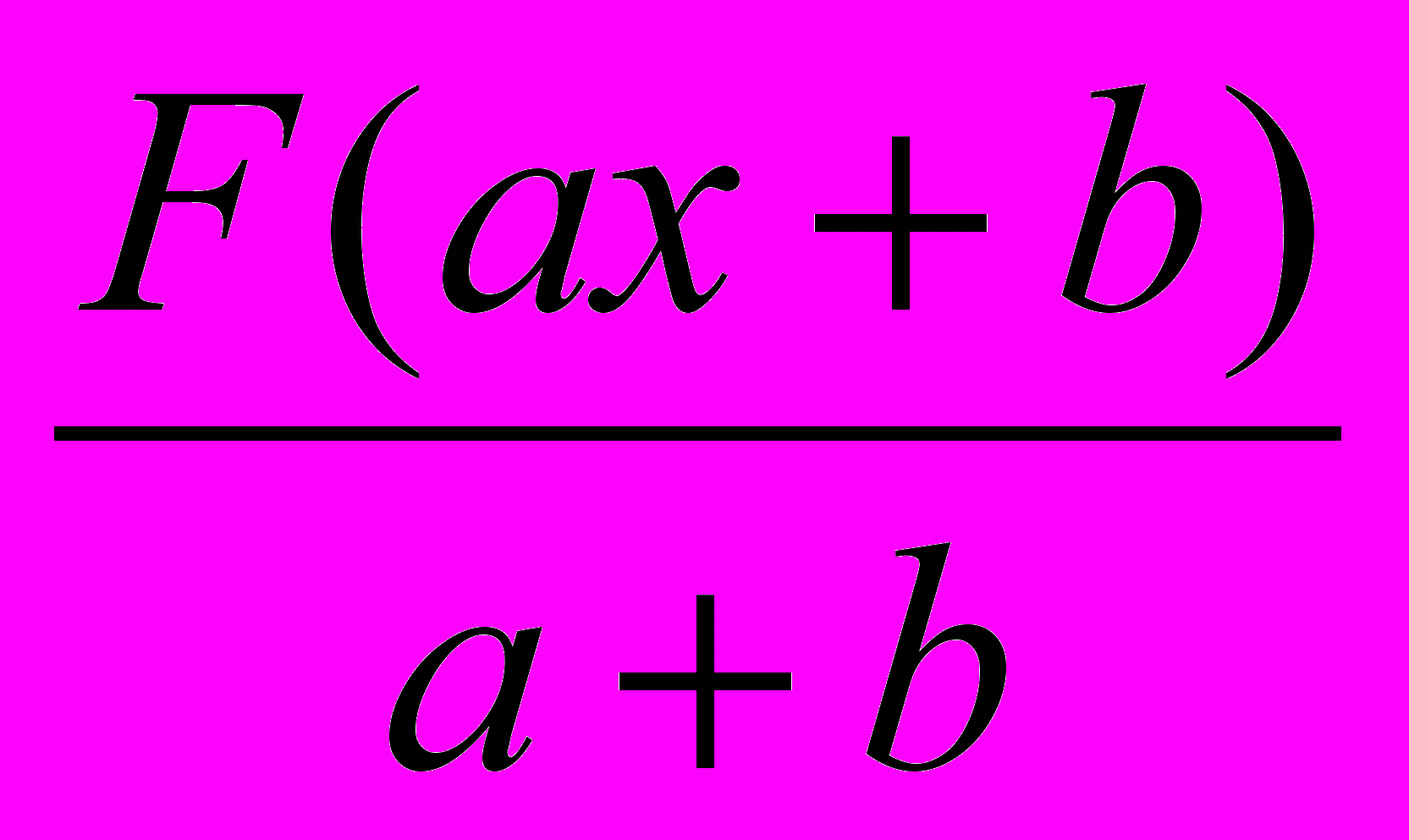 |
| 4. Пусть 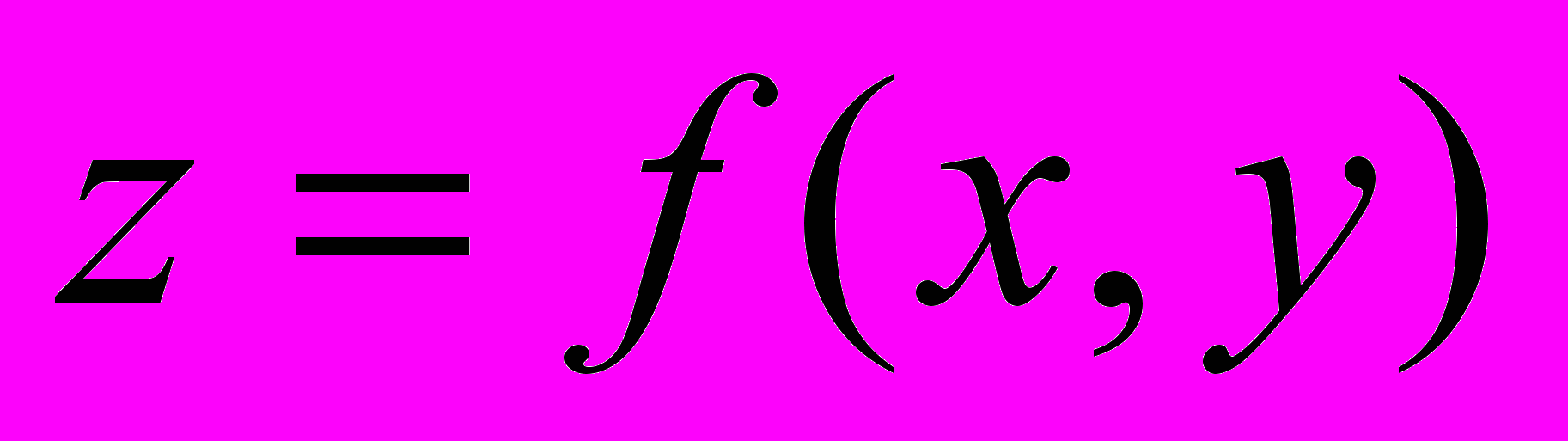 . Указать правильный ответ . Указать правильный ответ | 1. 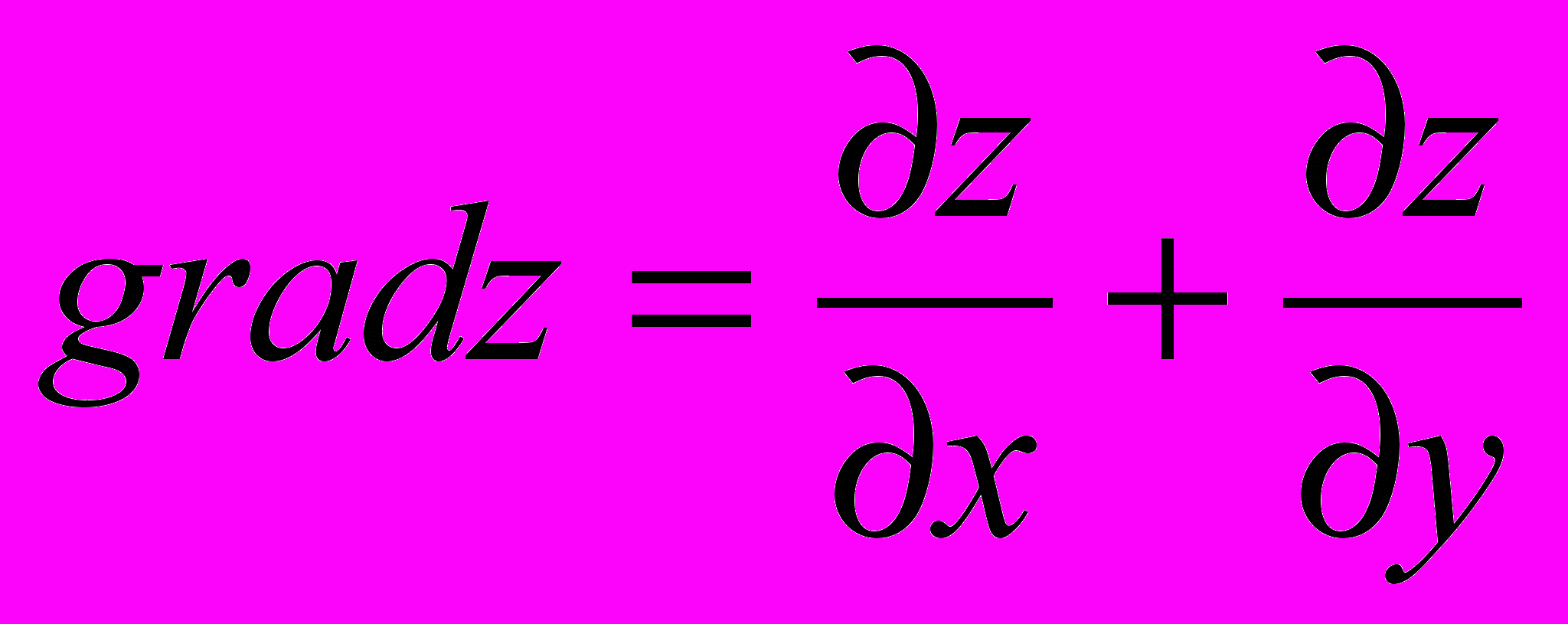 2. 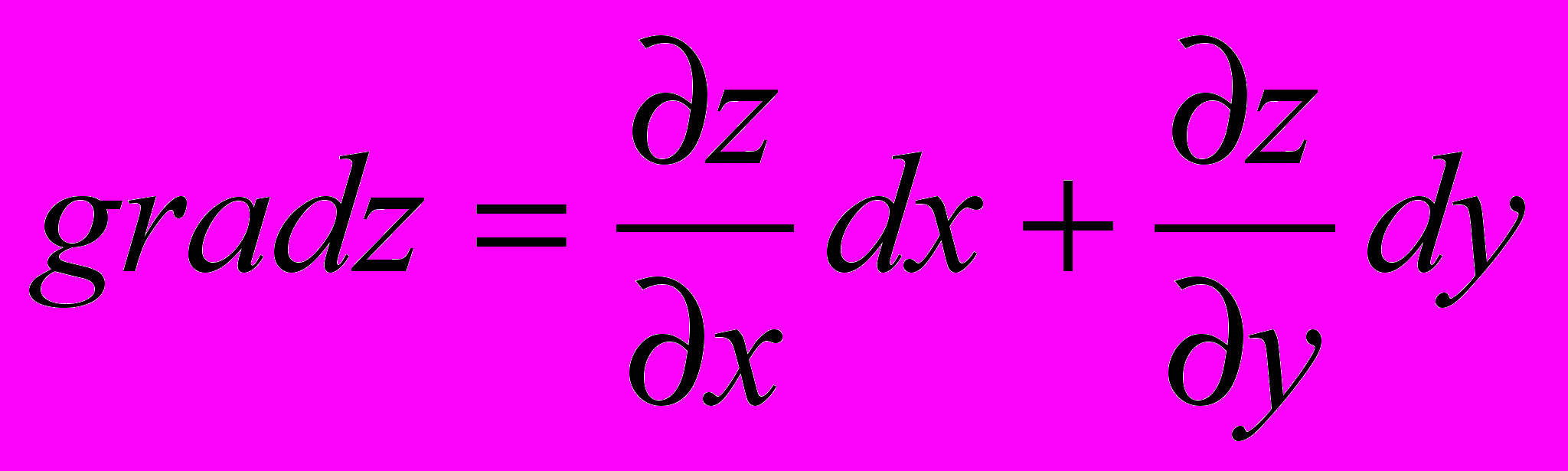 3. 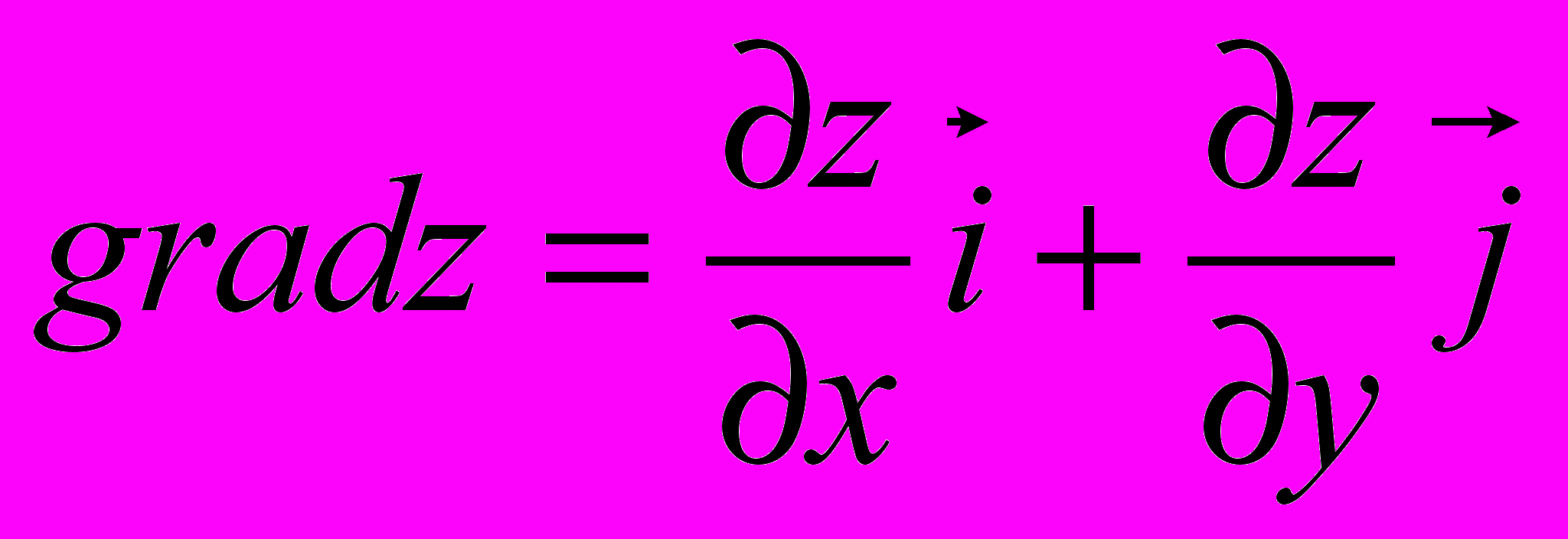 4. 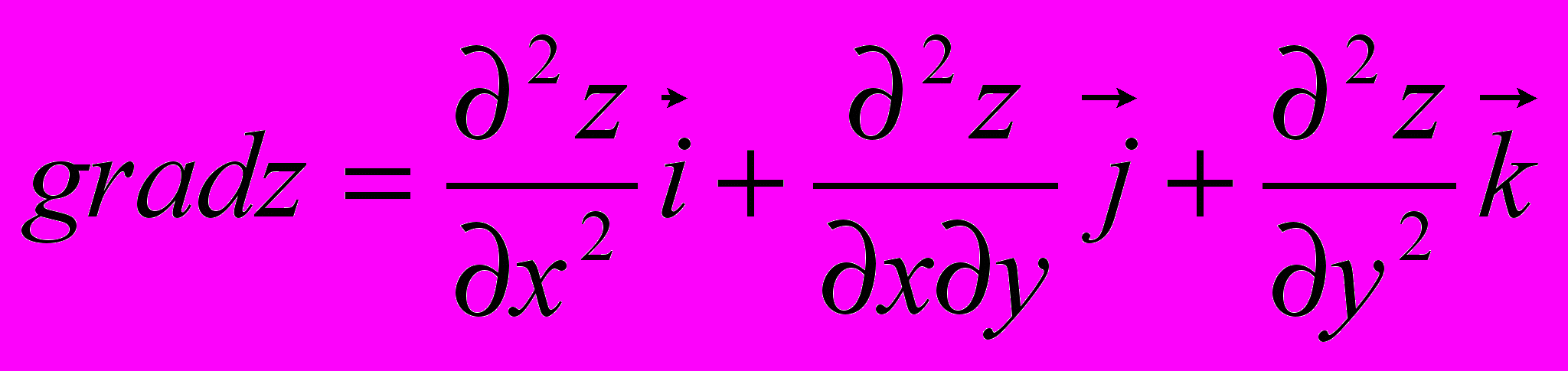 |
| 5. Дано дифференциальное уравнение 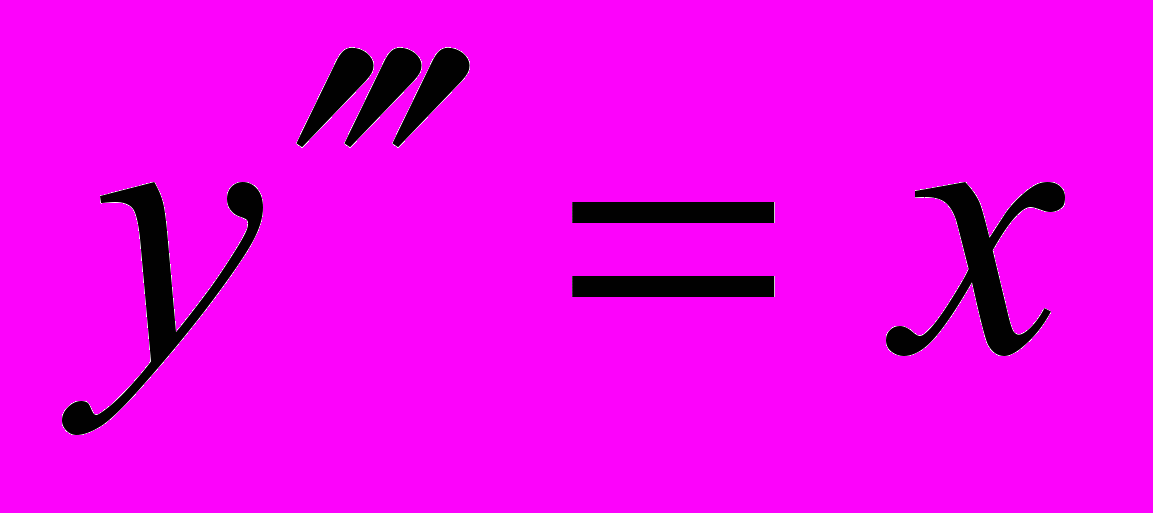 . Сколько произвольных постоянных должно содержать его общее решение? . Сколько произвольных постоянных должно содержать его общее решение? | 1. 0 2. 1 3. 2 4. 3 |
Задачи
7. Вычислить
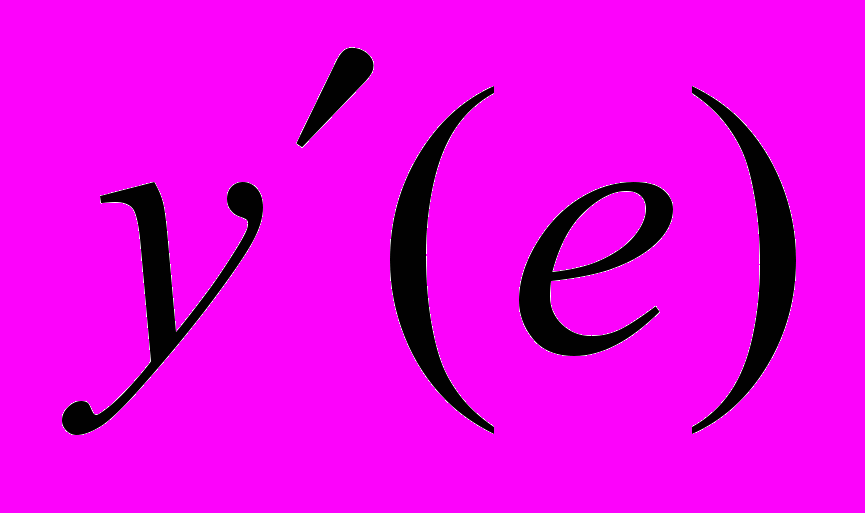 для функции
для функции 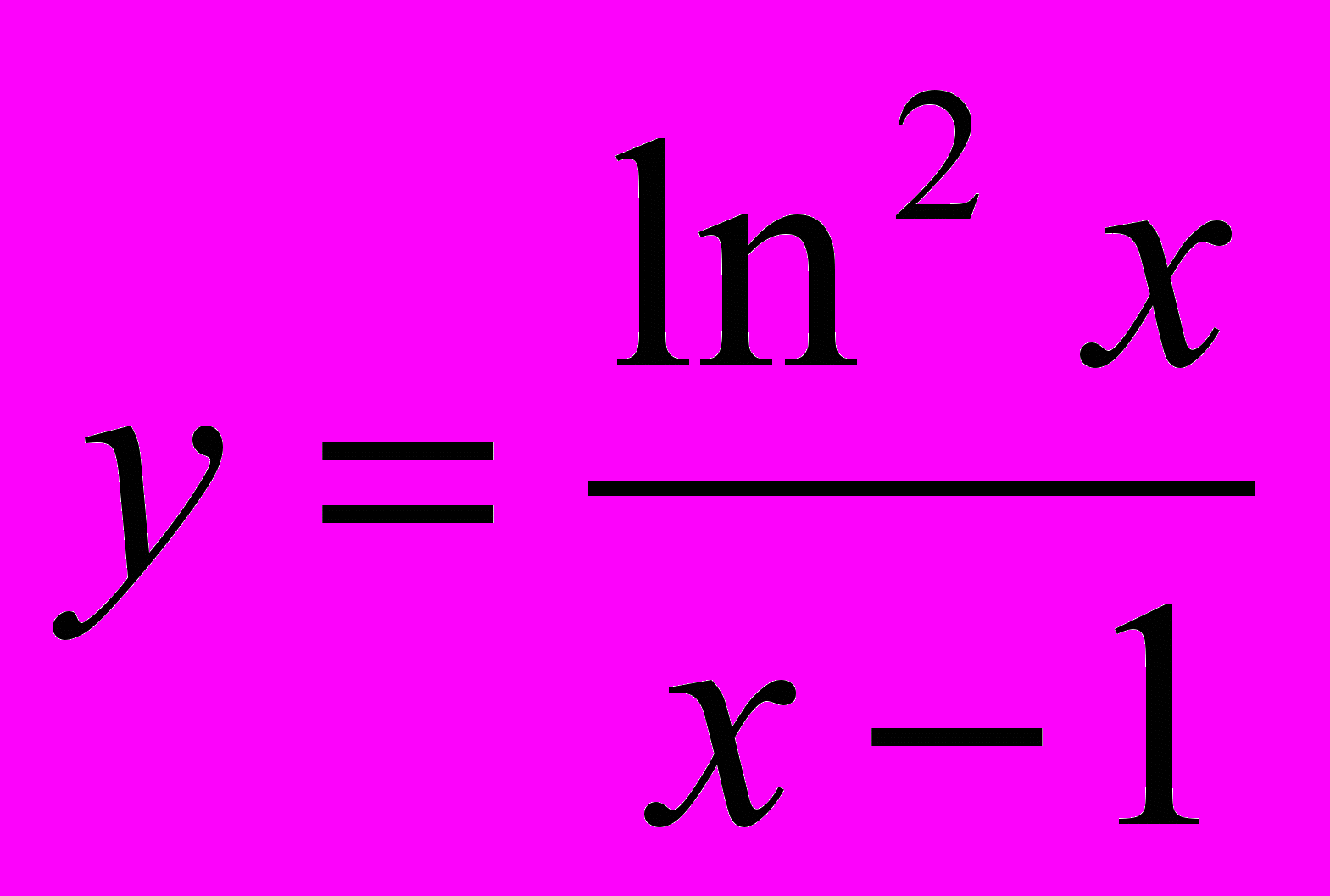 .
.8. Найти данный неопределенный интеграл
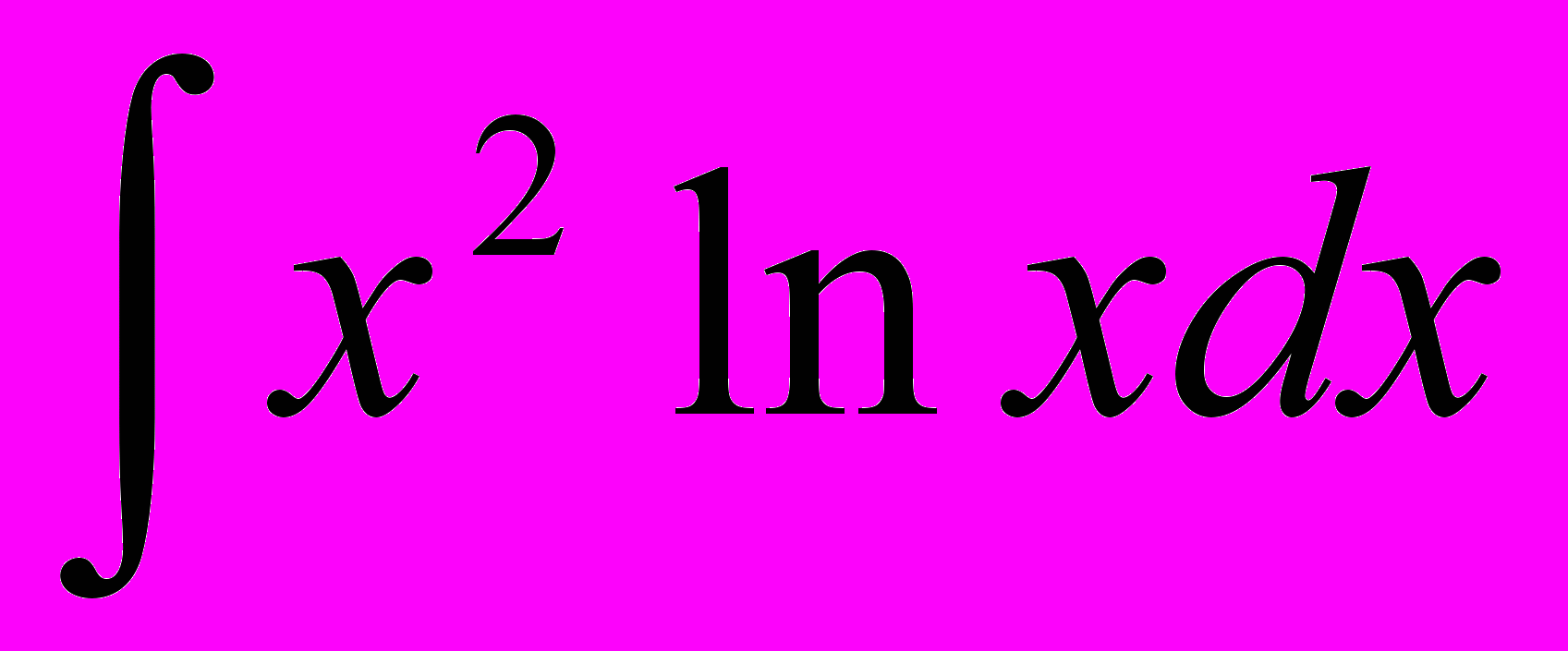 .
. 9. Вычислить данный определенный интеграл
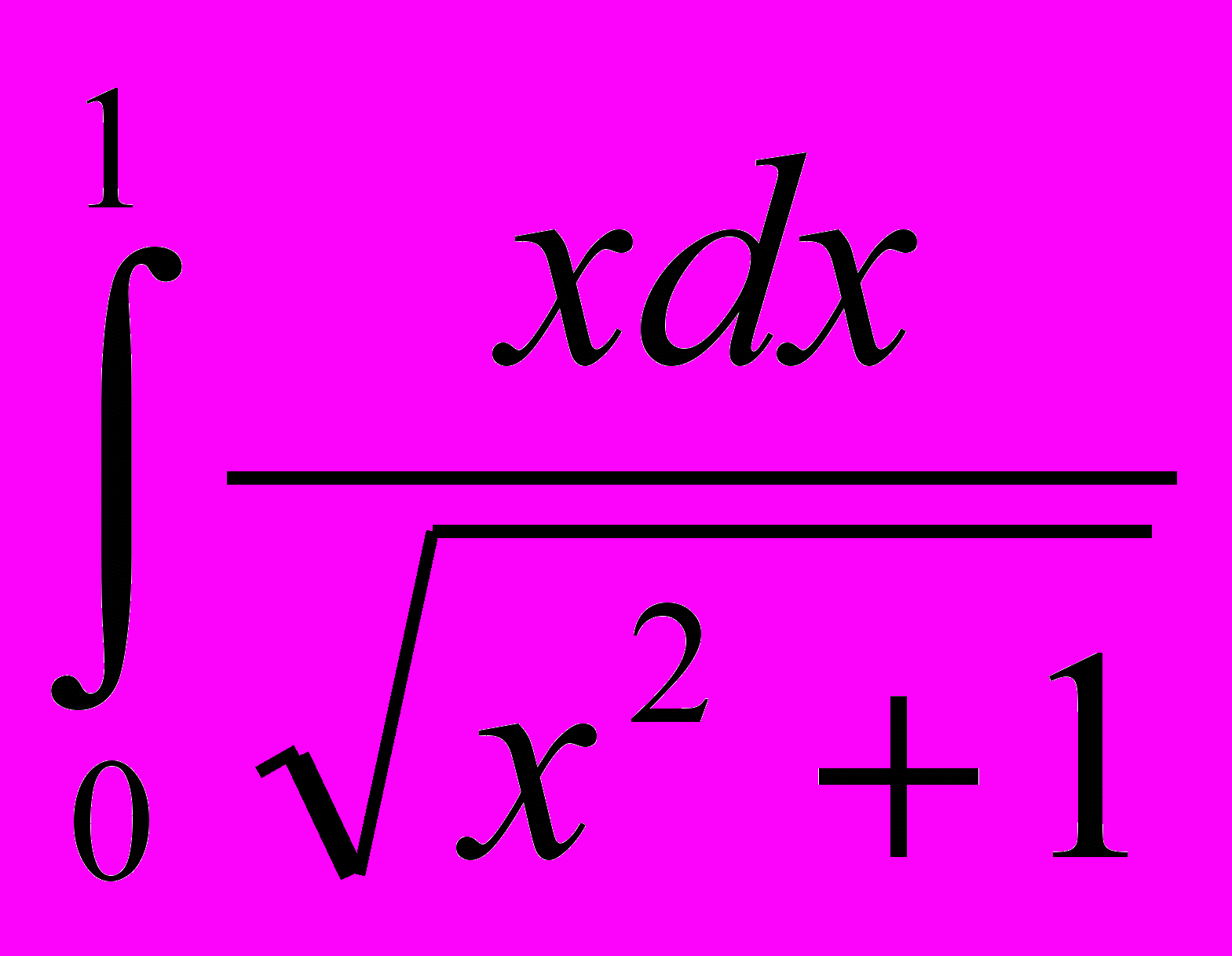
10. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям
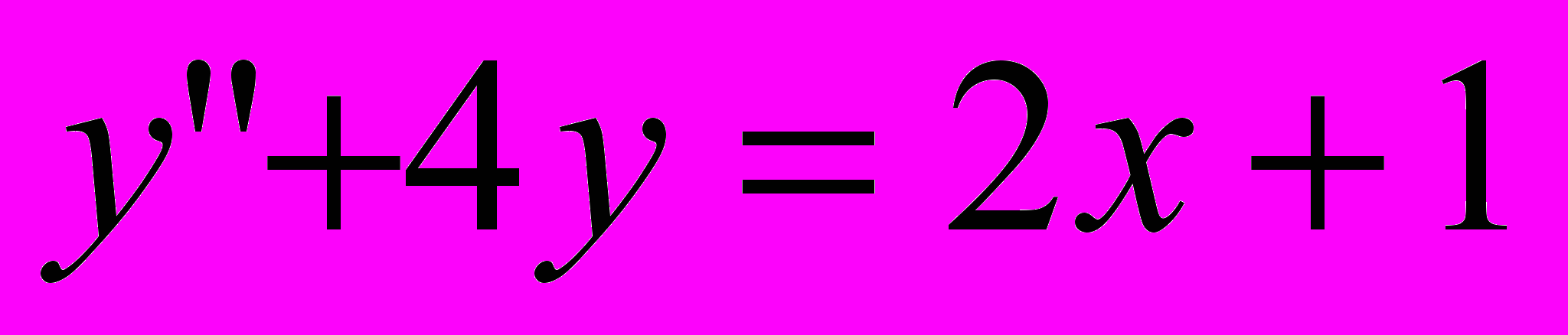 ,
, 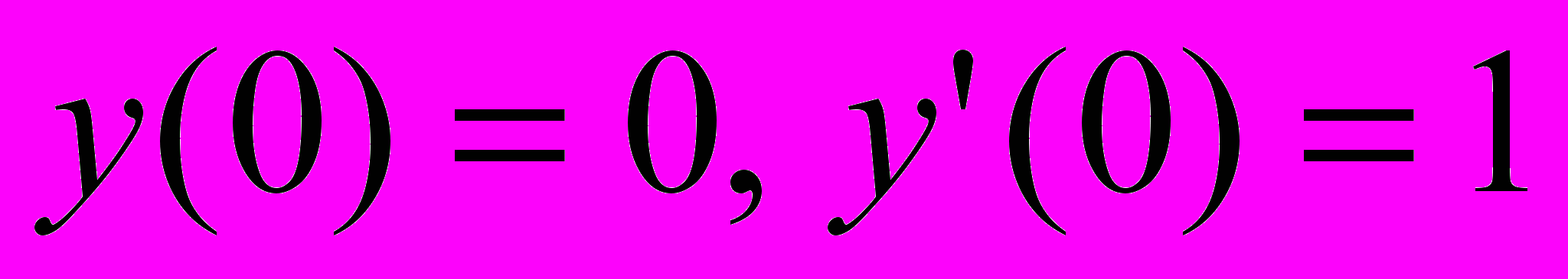 .
.11. Учебно-методическое и информационное обеспечение дисциплины:
Основная
- Минорский В.П. Сборник задач по высшей математике: Учебное пособие для втузов.-13-е изд.-М.: Наука,1987.-360 с.
- Пискунов Н.С. Дифференциальное и интегральное исчисления: Учебное пособие для втузов: В 2-х т. Т.1.Т.2.-Стереотип.изд. .-М:Интеграл-Пресс,2000.-415с.
- Мантуров О.В. Курс высшей математики: Ряды. Уравнения математической физики. Теория функций комплексной переменной. Численные методы. Теория вероятностей: Учебник для втузов.-.:Высш.шк.,1991.-448с.
Дополнительная:
- Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2 ч.: Учеб. пособие для вузов./Данко П.Е., Попов А.Г., Кожевникова Т.Я.- 3-е изд., пераб. и доп. - М.: Высш. шк.,1980.-320 с.
- Соломенцев Е.Д. Функции комплексного переменного и их применения: Учебное пособие для инженерно-техн. спец. вузов.-М.:Высш.шк., 1988.-167с.
- Бугров Я.С.,Никольский С.М. Высшая математика. Задачник: Учебное пособие для инженерно-техн.спец.вузов.-2-е изд.,испр.и доп.-М.:Наука,1987.-256с.
- Гусак А.А. Высшая математика: В 2т.:Учеб.для вузов.Т.1.-2-е изд.,испр. -Минск: ТетраСистемс,2000.-543с
Методические указания:
- Математика. Математический анализ: Метод. указ./Сост.: Б.Я.Солон -Иваново: ИГХТУ,2005.-42 с. № 939.
- Дифференциальные уравнения: Метод. указ./Сост.: Е.М. Михайлов. -Иваново: ИГХТУ,2009.-24 с. №371.
- Тесты по высшей математике. Часть 1: Метод. указ./Сост.: Е.В. Комарова, Е.Л. Никологорская. - Иваново: ИГХТУ,2009.-36 с. № 355.
Электронные учебные ресурсы:
- электронная версия конспекта лекций;
- информационно-справочная система «В помощь студентам» .ru.
12. Материально-техническое обеспечение дисциплины
Лекции по дисциплине проводятся в аудитории, оснащенной видеопроектором
Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению и профилю подготовки «Информационные системы и технологии».
Автор проф. Солон Б.Я. _____________ (подпись, ФИО)
Заведующий кафедрой Высшей математики
проф. Солон Б.Я. _____________ (подпись, ФИО) (подпись, ФИО)
Рецензент (ы) (подпись, ФИО)
Программа одобрена на заседании НМС ИГХТУ
от года, протокол № .
