Geum.ru

Рабочая программа учебной дисциплины «Математический анализ» Специальность «Математические методы в экономике (061800)»

Вид материалаРабочая программа

Содержание


Структура дисциплины
Наименование раздела и темы
Целью курса является
Содержание дисциплины
Практические занятия
Контрольная работа 1.
Подобный материал:


ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ


ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ»


Кафедра высшей математики


«УТВЕРЖДАЮ»

зав. кафедрой,

д. техн. наук, профессор

__________________________ Г. В. Савинов


РАБОЧАЯ ПРОГРАММА

учебной дисциплины


«Математический анализ»

Специальность «Математические методы в экономике (061800)»


Рассмотрена на заседании кафедры,

протокол №_____2___________

от «_17___» _октября___ 2006 г.


Санкт-Петербург

2006 г.

Утверждена Научно-методическим советом университета


Рабочая программа учебной дисциплины «Математический анализ». Специальность «Математические методы в экономике». ― СПб.: Изд-во СПбГУЭФ, 2006. ― 12 с.


Рабочая программа составлена в соответствии с учебным планом специальности «Математические методы в экономике», предназначена для студентов I курса дневной формы обучения.

Программа содержит тематику лекций и практических занятий, вопросы для самоконтроля, список обязательной и дополнительной литературы.


Автор-разработчик программы:

канд. физ.-мат. наук, доцент В. Г. Дмитриев


Рецензент:

доктор техн. наук, проф. Г. В. Савинов


 Издательство СПбГУЭФ 2006

СТРУКТУРА ДИСЦИПЛИНЫ




N

темы


Наименование раздела и темы
Количество часов

Лекции
Практ.

зан.
Контр. раб
Самост. раб.
Итого часов

1.
Введение в математический анализ
8
6



14
28

1.1.
Последовательности
3
2



5
10

1.2.
Элементы топологии пространства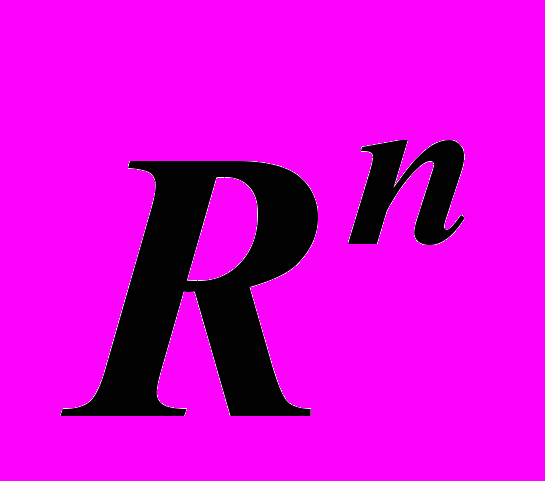

2






2
4

1.3.
Предел и непрерывность функций
3
4



7
14

2.
Дифференциальное исчисление функции одной переменной
10
8



18
36

2.1.
Дифференцирование функции одной переменной
2
4



6
12

2.2.
Свойства дифференцируемых функций
4






4
8

2.3.
Монотонность, экстремумы и выпуклость функции одной переменной
4
4



8
16

3
Интегральное исчисление функции одной переменной
8
6



14
28

3.1.
Неопределенный интеграл
4
4



8
16

3.2.
Определенный интеграл
4
2
2
10
18

4
Дифференцирование функций нескольких переменных
8
6



14
28

4.1.
Частные производные
4
4



8
16

4.2.
Дифференцируемые отображения
2






2
4

4.3.
Экстремумы и выпуклость функции нескольких переменных
2
2



4
8

5
Кратные интегралы
6
4



10
20

5.1.
Двойные и тройные интегралы
4
4



8
16

5.2.
Криволинейные и поверхностные интегралы
2






2
4

6
Числовые и функциональные ряды
6
6



12
24

6.1.
Числовые ряды
4
2



6
12

6.2.
Степенные ряды
2
4



6
12

7
Элементы теории дифференциальных уравнений
8
8



16
32

7.1
Обыкновенные дифференциальные уравнения
4
6



10
20

7.2.
Системы линейных дифференциальных уравнений с постоянными коэффициентами
2






2
4

7.3.
Обыкновенные разностные уравнения
2
2
2
8
14




ИТОГО
54
42
4
100
200



Дисциплина "Математический анализ" изучается на I курсе в течение II-го семестра, завершается экзаменом.


Целью курса является:

ознакомить студента с важнейшими математическими понятиями и утверждениями;

научить студента постановке математической модели стандартной задачи и анализу полученных знаний;

привить студенту определенную грамотность, достаточную для самостоятельной работы с экономико-математической литературой;

В результате изучения дисциплины студент должен овладеть:

а) фундаментальными математическими понятиями;

б) классическими методами решения основных математических задач, к которым могут приводить те или иные экономические проблемы;

в) навыками самостоятельной работы с математической литературой.


СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ




ТЕМА 1. Ведение в математический анализ


1.1. Последовательности

Определение и примеры числовой последовательности. Пределы числовой последовательности. Свойства сходящихся числовых последовательностей. Поведение монотонных и ограниченных числовых последовательностей. Число 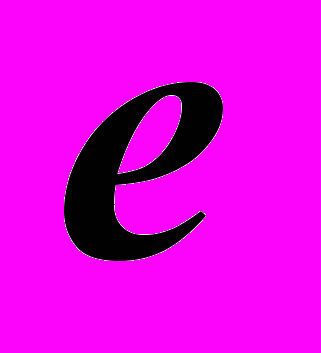. Векторные последовательности. Сходимость векторных последовательностей.

1.2. Элементы топологии пространства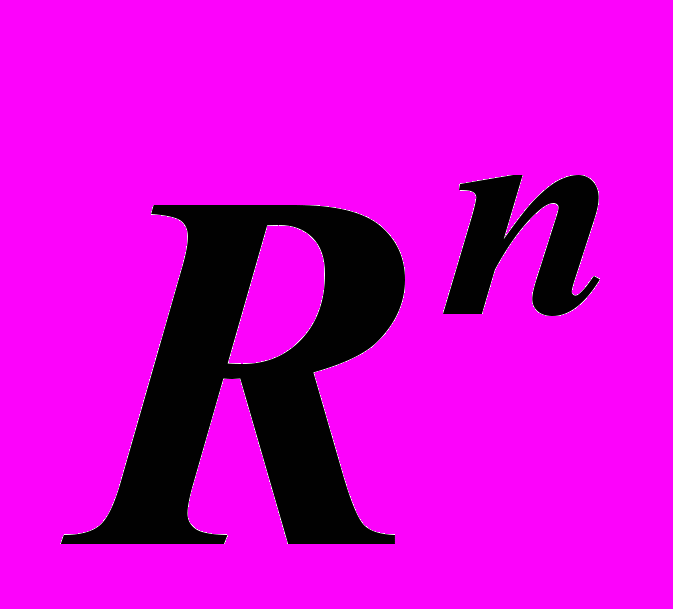


Открытые шары в пространстве 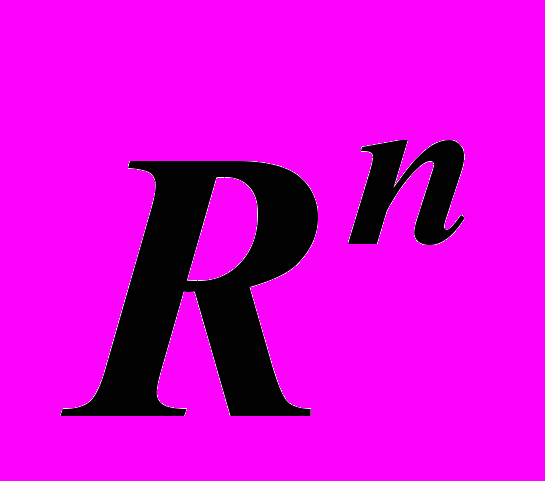. Классификация точек множества. Открытые и замкнутые множества, их свойства. Граница множества. Компактные множества. Выпуклые множества. Линейно связные множества.

1.3. Предел и непрерывность функций


Определение пределов функции. Свойства пределов. Односторонние пределы. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых. Непрерывность функции в точке. Свойства непрерывных функций. Примеры непрерывных функций. Односторонняя непрерывность. Понятие о точках разрыва и их классификации. Замечательные пределы. Свойства функций, непрерывных на компактном множестве.

ТЕМА 2. Дифференциальное исчисление функции одной переменной

2.1. Дифференцирование функции одной переменной


Определение производной функции в точке. Связь между непрерывностью и существованием конечной производной в точке. Односторонние производные. Дифференциал функции в точке, его связь с производной в точке. Производная функция. Дифференцирование алгебраических операций. Производная сложной и обратной функции. Дифференцирование функций, заданных параметрически. Производные и дифференциалы высших порядков.

2.2. Свойства дифференцируемых функций


Теоремы Ферма, Ролля, Лагранжа, Коши, Лопиталя. Теорема Тейлора. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений, оценка ошибки.

2.3. Монотонность, экстремумы и выпуклость функции одной переменной


Признаки монотонности функции одной переменной. Определение и признаки локальных экстремумов функции одной переменной. Задача оптимизации функции, дифференцируемой на замкнутом промежутке. Определение и признаки выпуклости функции одной переменной. Точки перегиба графика функции. Асимптоты графика функции одной переменной. Исследование функции одной переменной и построение графика.

ТЕМА 3. Интегральное исчисление функции одной переменной

3.1. Неопределенный интеграл


Первообразная и неопределенный интеграл. Линейные свойства операции неопределенного интегрирования, замена переменной и интегрирование по частям в неопределенном интеграле. Таблица неопределенных интегралов. Основные классы интегрируемых функций.

3.2. Определенный интеграл


Определение определенного интеграла и его свойства. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Применения определенного интеграла. Несобственные интегралы, признаки сходимости несобственных интегралов.



ТЕМА 4. Дифференцирование функций нескольких переменных

4.1. Частные производные


Определение частных производных первого порядка. Первый дифференциал (полная производная) функции нескольких переменных. Дифференцируемые функции нескольких переменных, условие дифференцируемости. Сложная функция нескольких переменных. Производная вдоль вектора и по направлению. Градиент и его свойства. Частные производные и дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных (без доказательства).

4.2. Дифференцируемые отображения


Отображения множеств из пространства 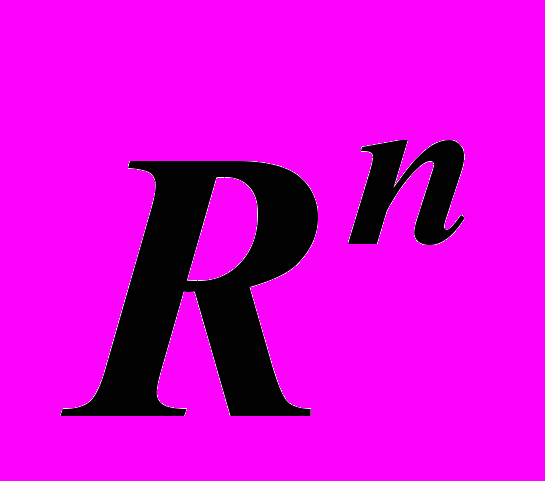в пространство 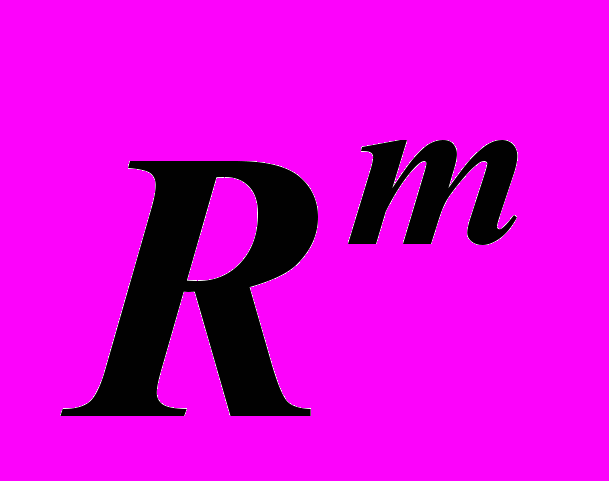. Непрерывные и дифференцируемые отображения. Якобиан отображения. Условие независимости системы функций. Неявные функции. Теорема существования (без доказательства). Дифференцирование неявной функции. Теорема об обратной функции нескольких переменных (без доказательства).

4.3. Экстремумы и выпуклость функции нескольких переменных


Определение локальных экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Условный экстремум. Метод множителей Лагранжа. Определение и признаки выпуклости функции нескольких переменных. Неравенство Иенсена.



ТЕМА 5. Кратные интегралы

5.1. Двойные и тройные интегралы


Повторные интегралы. Изменение порядка интегрирования в повторных интегралах. Двойной и тройной интегралы, определения и свойства. Сведение кратного интеграла к повторному. Понятие -кратного интеграла. Замена переменных в кратных интегралах.

5.2. Криволинейные и поверхностные интегралы


Понятие кривой. Гладкие и кусочно гладкие кривые. Длина кривой. Криволинейные интегралы. Их свойства и вычисление. Понятие поверхности. Касательная плоскость и нормаль к поверхности. Площадь поверхности. Поверхностные интегралы Их свойства и вычисление

ТЕМА 6. Числовые и функциональные ряды

6.1. Числовые ряды


Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами. Ряды с неотрицательными членами. Признаки сходимости. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютно сходящихся рядов

6.2. Степенные ряды


Понятие о функциональных рядах. Область сходимости. Равномерная сходимость. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Степенные ряды. Теорема Абеля. Круг сходимости. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. Приложение рядов.

ТЕМА 7. Элементы теории дифференциальных уравнений



7.1. Обыкновенные дифференциальные уравнения


Определение дифференциального уравнения. Порядок уравнения. Решения дифференциального уравнения. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах. Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения. Общее решение. Фундаментальная система решений. Метод Лагранжа вариации постоянных. Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида

7.2. Системы линейных дифференциальных уравнений с постоянными коэффициентами


Нормальная система дифференциальных уравнений. Векторная запись нормальной системы. Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Системы линейных дифференциальных уравнений с постоянными коэффициентами. Понятие о качественной теории дифференциальных уравнений, фазовое пространство (плоскость), фазовая траектория и скорость.

7.3. Обыкновенные разностные уравнения


Разностные уравнения с постоянными коэффициентами. Методы решений разностных уравнений.



ПРАКТИЧЕСКИЕ ЗАНЯТИЯ




ТЕМА 1. Ведение в математический анализ


1.1. Последовательности

Примеры числовых последовательностей. Вычисление пределов числовых последовательностей.

1.3. Предел и непрерывность функций


Доказательство пределов с помощью определений. Примеры бесконечно малых и бесконечно больших функций. Эквивалентные бесконечно малые. Вычисление пределов. Примеры непрерывных функций.

ТЕМА 2. Дифференциальное исчисление функции одной переменной

2.1. Дифференцирование функции одной переменной


Вычисление производных с помощью определения. Таблица производных. Техника дифференцирования. Дифференцирование функций, заданных параметрически. Производные и дифференциалы высших порядков.

2.2. Свойства дифференцируемых функций


Разложение элементарных функций по формулам Тейлора и Мак-Лорена. Применение формулы Тейлора для приближенных вычислений, оценка ошибки.

2.3. Монотонность, экстремумы и выпуклость функции одной переменной


Вычисление промежутков монотонности и локальных экстремумов функции одной переменной. Задача оптимизации функции на замкнутом промежутке. Вычисление промежутков выпуклости и точек перегиба функции одной переменной. Асимптоты графика функции одной переменной. Исследование функции одной переменной и построение графика.

ТЕМА 3. Интегральное исчисление функции одной переменной

3.1. Неопределенный интеграл


Таблица неопределенных интегралов. Замена переменной и интегрирование по частям в неопределенном интеграле. Вычисление неопределенных интегралов. Основные классы интегрируемых функций.

3.2. Определенный интеграл


Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Применения определенного интеграла. Несобственные интегралы, признаки сходимости несобственных интегралов.


Контрольная работа 1. Вычисление пределов, производных, исследование функции и построение графика. Неопределенные и определенные интегралы.



ТЕМА 4. Дифференцирование функций нескольких переменных

4.1. Частные производные


Вычисление частных производных первого порядка. Сложная функция нескольких переменных. Производная вдоль вектора и по направлению. Градиент и его свойства. Частные производные и дифференциалы высших порядков.

4.3. Экстремумы и выпуклость функции нескольких переменных


Вычисление локальных экстремумы функций нескольких переменных. Условный экстремум. Метод множителей Лагранжа.

ТЕМА 5. Кратные, криволинейные и поверхностные интегралы

5.1. Кратные интегралы


Повторные интегралы. Изменение порядка интегрирования в повторных интегралах. вычисление двойных и тройных интегралов.

ТЕМА 6. Числовые и функциональные ряды

6.1. Числовые ряды


Ряды с неотрицательными членами. Признаки сходимости. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости. Признак Лейбница. Исследование сходимости числовых рядов.

6.2. Степенные ряды


Исследование сходимости степенных рядов. Разложение функций в степенные ряды. Приложение рядов.

ТЕМА 7. Элементы теории дифференциальных уравнений

7.1. Обыкновенные дифференциальные уравнения


Решение дифференциальных уравнений первого порядка. Уравнения с разделяющимися переменными, линейные и однородные уравнения. Дифференциальные уравнения второго порядка, допускающие понижение порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения с правой частью специального вида

7.2. Обыкновенные разностные уравнения с постоянными коэффициентами


Решение разностных уравнений с постоянными коэффициентами.


Контрольная работа 2. Частные производные, производная по направлению и градиент, локальные экстремумы функции нескольких переменных. Двойные интегралы. Дифференциальные уравнения.


ЛИТЕРАТУРА


Темы 1 - 7

Основная.
  1. Бугров Я.С. , Никольский С.М. Дифференциальное и интегральное исчисление. –М. :Наука ,1980.
  2. Бугров Я.С. Никольский С.М. Высшая математика: Задачник. -М.: Наука , 1982.
  3. Бугров Я.С. Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ФКП. –М.: Наука , 1981.
  4. Ведина О.И., Десницкая В.Н., Варфоломеева Г.Б., Тарасюк А.Ф. Математика. Математический анализ для экономистов. –М.: Филинь, 2000
  5. Высшая математика для экономистов/Под ред. Кремера Н.Ш., - М.: ЮНИТИ, 1998.
  6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Уч. пособие. Ч.1,2.-1980
  7. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. -М.: Высшая математика, 1982
  8. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учебник.-М., Гос.Изд.физ-мат.литература,1983
  9. Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты). –М.: Высшая школа, 1983
  10. Математика в экономике: учебно-методическое пособие. Под ред. Н.Ш Кремера. – М.: Финстатинформ, 1999.
  11. Солодовников А. С., Бабайцев В. А.,Браилов А. В.,Шандра И. Г.Математика в экономике: Учебник: В 2-х ч. Ч. 2.—М.: Финансы и статистика, 1999.—376 с.:ил.


Дополнительная.
  1. Зорич В.А. Математический анализ. Ч. 1, М., 1982. Ч. 2. 1984.
  2. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. М., 1971. Ч. 2, М., 1980.
  3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М., 1969.
  4. Рудин У. Основы математического анализа. М., 1966.
  5. Смирнов В.И. Курс высшей математики. Т. 1, 2, 5. М., 1961-1966.
  6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1-3. М., 1966-1971.