Geum.ru

Программа по дисциплине математический анализ

Вид материалаПрограмма

Содержание


Перечень дисциплин, усвоение которых студентам необходимо для усвоения курса
В результате изучения курса студент должен
Содержание курса
Тема 2. Действительные числа
Тема 3. Числовая последовательность
Тема 4. Комплексные числа
Тема 5. Мощность множества
Тема 6. Алгебраические многочлены
Тема 8. Предел функции
Тема 9.  Непрерывность функции
Тема 10. Производная и дифференциал
Тема 11. Основные теоремы о свойствах дифференцируемых функций
Тема 12. Производные и дифференциалы высших порядков. Раскрытие неопределенностей
Тема 13. Формула Тейлора
Тема 14. Возрастание и убывание функции. Локальные экстремумы
Тема 15. Вогнутость и выпуклость функции. Точки перегиба
Тема 16. Применение дифференциального исчисления для исследования функций и построения их графиков
Тема 17. Неопределённые интегралы
Тема 18. Определенные интегралы
Тема 19. Несобственные интегралы
...
Полное содержание
Подобный материал:
УЧЕБНАЯ ПРОГРАММА ПО ДИСЦИПЛИНЕ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Крюковский А.С., Келлин Н.С


Требования ГОС к обязательному минимуму содержания основной

образовательной программы:

дифференциальное и интегральное исчисления, элементы теории функций и функционального анализа, теория функций комплексного переменного.


Цели преподавания дисциплины:

Знакомство с основными понятиями, положениями и методами дифференциального и интегрального исчисления, теории функций и функционального анализа, теории функций комплексного переменного, получение навыков построения математических доказательств путем логически непротиворечивых рассуждений, навыков решения прикладных задач.

Перечень дисциплин, усвоение которых студентам необходимо для усвоения курса

Для изучения дисциплины «Математический анализ» студент должен иметь математическое образование в объёме программы средней школы и иметь навыки самостоятельной работы.

В результате изучения курса студент должен

знать:
  • базовые понятия и теоремы, дифференциального и интегрального исчисления функций одного и нескольких переменных, теории числовых и функциональных рядов;

уметь:
  • применять полученные знания к решению задач дифференциального и интегрального исчислении функций одной и нескольких переменных;
  • применять полученные знания к решению задач к исследованию функциональных зависимостей и построению графиков функций;
  • применять полученные знания к решению задач теории числовых и функциональных рядов, определять условия их сходимости, уметь анализировать свойства функций с помощью степенных рядов и рядов Фурье.

иметь представление о:
  • месте и роли математики в современном мире, мировой культуре и истории; о математическом мышлении, индукции и дедукции в математике, принципах математических рассуждений и математических доказательств; об основных понятиях дифференциального и интегрального исчисления, теории функций и функционального анализа, теории функций комплексного переменного

Основными видами занятий являются лекции, семинарские занятия и самостоятельная работа

Основными видами промежуточного контроля знаний являются: контрольные домашние задания

Основными видами рубежного контроля знаний являются : в конце 1-го семестра предусмотрен зачет, в конце 2-го семестра — экзамен.




Часы, отведенные на изучение дисциплины, согласно учебному плану (252ч):

Форма обучения
Всего ауд. занятий
Самостоятельная работа

очная
144ч
108ч

очно-заочная(вечерняя)
90ч
162ч

заочная
24ч
228ч



СОДЕРЖАНИЕ КУРСА




Тема 1. Множества

Основные черты математического мышления, аксиоматический подход, математические доказательства, прямая, обратная и противоположная теоремы. Индукция и дедукция, бином Ньютона. Элементы и множества, конечные и бесконечные множества, отношения и отображения. Операции над множествами. Понятие размерности, множества дробной размерности.

Тема 2. Действительные числа

Натуральный ряд чисел, целые числа, рациональные числа. Иррациональные числа, степени и корни, логарифмы. Действительные (вещественные) числа. Аксиоматическое определение действительных чисел. Понятие группы, кольца, поля. Числовая ось. Абсолютные величины. Интервал, отрезок, окрестность точки.

Тема 3. Числовая последовательность

Определение числовой последовательности. Монотонные последовательности, возрастающие и убывающие, невозрастающие и неубывающие, ограниченные и неограниченные числовые последовательности. Понятие верхней и нижней граней. Бесконечно большие и бесконечно малые последовательности, связь между ними.

Предел числовой последовательности и его свойства. Признаки существования предела, существование предела у монотонной ограниченной последовательности. Число e. Подпоследовательности. Частичные пределы. Теорема Больцано–Вейерштрасса о существовании частичного предела у ограниченной последовательности. Критерий Коши. Бесконечно малые последовательности. Теоремы о арифметических действиях над сходящимися последовательностями. Предельный переход в неравенствах сходящихся последовательностей. Роль числовых последовательностей в вычислительных процессах.

Тема 4. Комплексные числа

Определение комплексных чисел, действия с ними. Поле комплексных чисел. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Эйлера. Показательная форма комплексного числа. Извлечение корня из комплексного числа. Логарифм комплексного числа.

Тема 5. Мощность множества

Десятичные дроби. Мощность множества. Счётные и континуальные множества. Равномощность целых, рациональных и натуральных чисел. Равномощность действительных и комплексных чисел. Равномощность множества точек прямой и n-мерного пространства.

Тема 6. Алгебраические многочлены

Определение многочленов. Корни многочленов. Деление многочленов (алгоритм Евклида). Теорема Безу. Основная теорема алгебры. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители. Кольцо многочленов.

Тема 7. Функция

Определение функции, область ее определения и область значений. Характеристики поведения функций: четность и нечетность, возрастание и убывание, наибольшее и наименьшее значения, ограниченность, периодичность. Основные элементарные функции, их свойства и графики. Замечательные кривые. Неявные функции. Сложные и обратные функции, их графики.

Тема 8. Предел функции

Предел функции в точке. Эквивалентность определения пределов в смысле Гейне и в смысле Коши. Предел функции на бесконечности. Предел слева и справа. Свойства пределов: арифметические действия над функциями, имеющими пределы, предельные переходы в неравенствах функций, имеющих пределы. Предел монотонной функции. Критерий Коши. Некоторые замечательные пределы. Односторонние пределы. Бесконечно малые и бесконечно большие функции. Эквивалентность функций, главная часть функции, омалое и Обольшое. Предел функции нескольких переменных

Тема 9.  Непрерывность функции

Непрерывность функции, непрерывность слева и справа. Выколотая точка, точки разрыва первого и второго рода. Арифметические действия над непрерывными функциями, непрерывность сложной функции. Кольцо непрерывных на отрезке функций. Свойства непрерывных функций, теорема об обращении функции в нуль (первая теорема Больцано–Коши), теорема о промежуточном значении (вторая теорема Больцано–Коши), теорема об ограниченности функции (первая теорема Вейерштрасса), теорема о достижении непрерывной функции в замкнутом промежутке верхней и нижней граней (вторая теорема Вейерштрасса). Непрерывность основных элементарных функций. Теорема об обратной функции.

Тема 10. Производная и дифференциал

Приращение функции, производная, дифференцируемость функции. Непрерывность дифференцируемой функции. Геометрический смысл производной, уравнения касательной и нормали. Дифференциал функции, его геометрический смысл. Инвариантность формулы для вычисления дифференциала первого порядка. Правила дифференцирования. Формулы дифференцирования основных элементарных функций. Производные сложной и обратной функции. Логарифмическое дифференцирование. Производная от неявной функции. Дифференцирование функций, заданных параметрически. Дифференцирование определителя матрицы.

Тема 11. Основные теоремы о свойствах дифференцируемых функций

Точки экстремума функции. Теоремы Ферма, Ролля, Лагранжа (теорема о среднем) и Коши, формулы Лагранжа и Коши, их применение.

Тема 12. Производные и дифференциалы высших порядков. Раскрытие неопределенностей

Производные и дифференциалы высших порядков. Нарушение инвариантности формы для дифференциалов высших порядков. Формула Лейбница. Раскрытие неопределенностей, неопределенности вида / и 0/0. Правило Лопиталя.

Тема 13. Формула Тейлора

Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа. Формула Маклорена. Представление основных элементарных функций exp(x), sin(x), cos(x), sh(x), ch(x), ln(1+x), (1+x) по формуле Маклорена. Применение формулы Тейлора в вычислительной математике.

Тема 14. Возрастание и убывание функции. Локальные экстремумы

Достаточный признак возрастания (убывания) функции одной переменной. Экстремумы функции (максимум и минимум). Необходимое условие экстремума, достаточные признаки экстремума. Наибольшее и наименьшее значения функции на отрезке.

Тема 15. Вогнутость и выпуклость функции. Точки перегиба

Определение выпуклой (вогнутой) функции, и точки перегиба графика функции. Необходимое условие точки перегиба. Достаточные признаки вогнутости (выпуклости) и наличия точек перегиба. Касательная к графику функции в точке перегиба.

Тема 16. Применение дифференциального исчисления для исследования функций и построения их графиков

Асимптоты графика функции (вертикальная, горизонтальная, наклонная). Понятие об асимптотическом разложении. Общая схема исследования функции и построения ее графика.

Тема 17. Неопределённые интегралы

Первообразная, неопределенный интеграл, его свойства. Замена переменной в неопределенном интеграле. Формула интегрирования «по частям». Интегрирование простейших рациональных дробей. Разложение правильной рациональной дроби на простейшие: случаи неповторяющихся линейных действительных множителей знаменателя и неповторяющихся квадратичных его множителей. Интегрирование тригонометрических и простейших иррациональных функций. Примеры функций, не имеющих элементарных первообразных.

Тема 18. Определенные интегралы

Интегральные суммы Римана и Дарбу. Определенный интеграл, его геометрический смысл, свойства. Необходимое и достаточное условие интегрируемости. Геометрический смысл определенного интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Формулы замены переменной и интегрирования «по частям» для определенного интеграла. Применение определенного интеграла к вычислению площадей плоских фигур (в декартовых и полярных координатах), длин дуг кривых, объёмов тел вращений. Методы приближенных вычислений определенных интегралов по формулам прямоугольников, трапеций и Симпсона.

Тема 19. Несобственные интегралы

Несобственные интегралы с бесконечными пределами и от неограниченных функций, их основные свойства. Признаки сходимости несобственных интегралов.

Тема 20. Функции нескольких переменных, предел, непрерывность

Понятие функции нескольких переменных, область определения и значения. Предел функции. Повторные пределы. Непрерывность.

Тема 21. Дифференцирование функций нескольких переменных

Частные производные. Геометрический смысл частных производных. Полное приращение функции, дифференцируемость функции. Полный дифференциал, его связь с частными производными. Инвариантность формы полного дифференциала первого порядка. Производная по направлению, градиент функции, его связь с производной по направлению. Геометрический смысл полного дифференциала. Частные производные и дифференциалы высших порядков. Основные понятия векторного анализа: градиент, ротор, дивергенция, оператор Лапласа. Формула Тейлора. Неявные функции. Теоремы существования. Дифференцирование неявных функций. Касательная плоскость и нормаль к поверхности.

Тема 22. Дифференцирование функции комплексной переменной

Дифференцируемость функции комплексного аргумента. Производная. Условия Коши-Римана. Геометрический смысл производной. Однолистные отображения. Конформные отображения.

Тема 23. Локальные экстремумы функций нескольких переменных. Условные экстремумы

Локальные экстремумы функций нескольких переменных, необходимые и достаточные условия экстремума. Условный экстремум, метод множителей Лагранжа определения условного экстремума. Примеры применения теории экстремумов при поиске оптимальных решений. Основные понятия теории катастроф: применение теории катастроф в физике, биологии, экологии, экономике, прогнозировании социальных явлений.

Тема  24. Кратные интегралы

Двойные и тройные интегралы, их свойства. Геометрический смысл двойного интеграла. Вычисление кратных интегралов повторным интегрированием. Замена переменных в двойных и тройных интегралах. Переход к полярной, цилиндрической и сферической системам координат. Вычисление площади поверхности и объема.

Тема  25. Криволинейные и поверхностные интегралы

Криволинейные интегралы первого рода, вычисление длины дуги пространственной кривой. Криволинейные интегралы второго рода, случай полного дифференциала, формула Грина. Поверхностные интегралы первого и второго рода, формула Стокса, формула Гаусса-Остроградского.

Тема  26. Интегрирование функции комплексного переменного

Представление интеграла функции комплексного переменного в виде контурного. Свойства интеграла от комплексной функции. Независимость от пути интегрирования. Интегральная теорема Коши. Интегральные формулы Коши.

Тема  27. Числовые ряды

Понятие числового ряда, частичные суммы, определение сходимости и расходимости числового ряда. Сумма числового ряда как предел последовательности частичных сумм. Сумма членов бесконечной убывающей геометрической прогрессии. Свойства сходящихся рядов. Критерий Коши. Необходимое условие сходимости ряда. Гармонический ряд. Признаки сравнения. Признаки сходимости знакопостоянных рядов: признак Д'Аламбера, признак Коши, признак Гаусса, интегральный признак. Обобщенный гармонический ряд 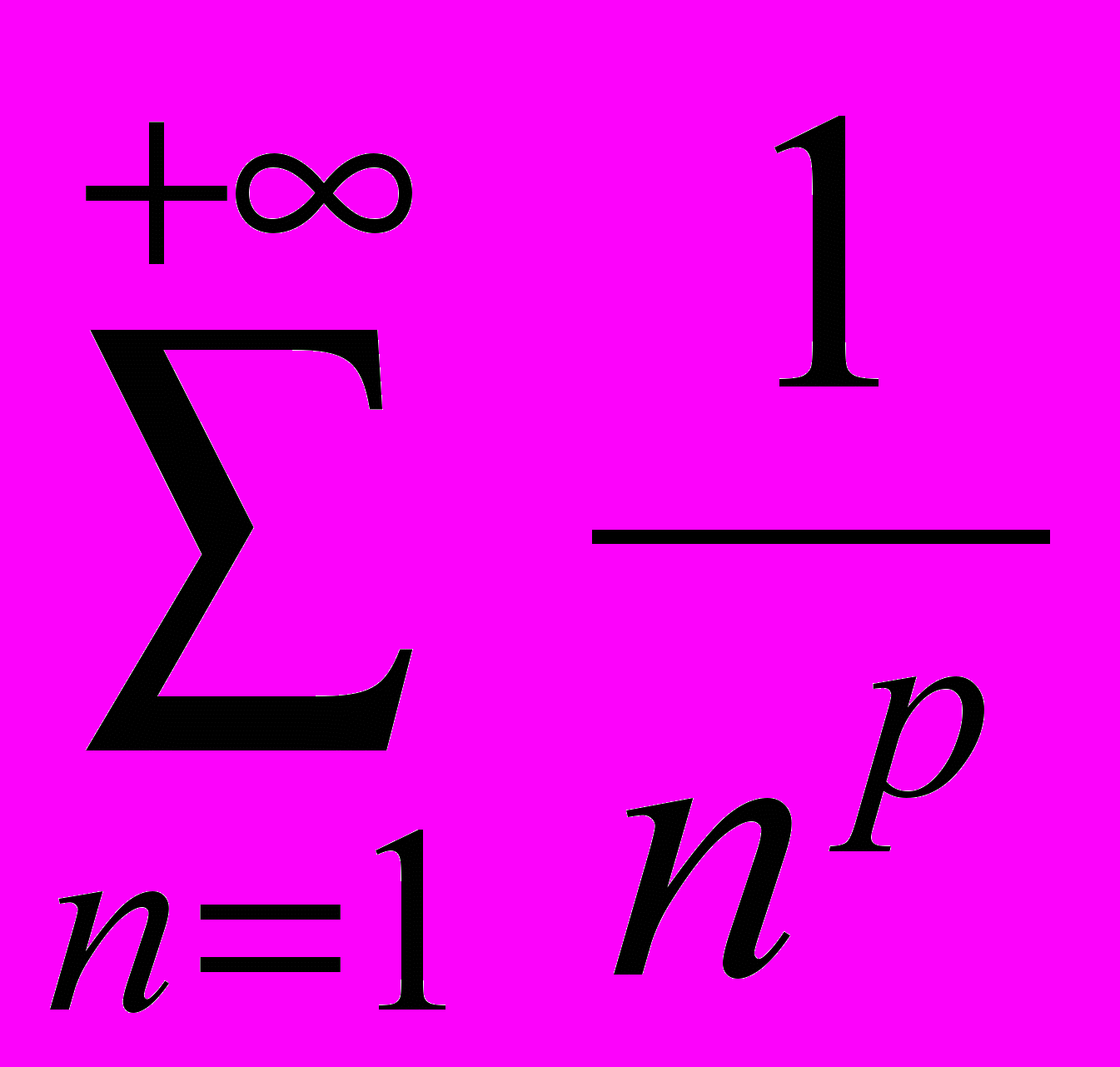. Знакочередующиеся ряды, признак Лейбница. Абсолютная и условная сходимости числовых рядов. Достаточные признаки сходимости знакопеременных рядов, признаки Дирихле и Абеля. Действия с рядами.

Тема  28. Функциональные ряды

Функциональные последовательности и ряды, область сходимости, методы ее определения. Равномерная сходимость. Критерий Коши. Необходимое условие равномерной сходимости функционального ряда. Признак равномерной сходимости Вейерштрасса, признаки Дирихле и Абеля. Свойства функциональных последовательностей и рядов, дифференцирование и интегрирование функциональных рядов.

Тема  29. Степенные ряды

Степенные ряды, радиус сходимости степенных рядов, равномерная сходимость степенного ряда внутри интервала сходимости. Формулы Д’Аламбера и Коши–Адамара для вычисления радиусов сходимости степенных рядов. Аналитические функции. Разложение функций в степенные ряды, ряды Тейлора. Дифференцирование и интегрирование степенных рядов. Применение степенных рядов в приближенных вычислениях.

Тема  30. Ряды Лорана

Регулярная и главная части рядов Лорана. Классификация особых точек. Большая теорема Пикара. Понятие вычета. Вычисление некоторых определенных интегралов с помощью теории вычетов.

Тема  31. Тригонометрические ряды

Тригонометрические ряды Фурье. Разложение функций в тригонометрические ряды Фурье. Условие поточечной сходимости и сходимости «в среднем». Теорема Дирихле. Ряды Фурье в случае произвольного интервала. Особенности разложения в ряд Фурье чётной и нечётной функции. Применение тригонометрических рядов Фурье в приближенных вычислениях. Понятие о преобразовании Фурье. Интеграл Фурье. Косинус- и синус преобразование Фурье.

Тема  32. Метрические пространства

Основные понятия, примеры; открытые и замкнутые множества; сепарабельность. Полные метрические пространства. Принцип сжатых отображений. Компактность в метрических пространствах (критерий Хаусдорфа, непрерывные функции на компактах; теорема Арцела).




ТЕМА 33. Линейные нормированные пространства

Понятие линейное пространство. Изоморфизм и изометрия. Задача о наилучшем приближении. Линейные функционалы (основные понятия, примеры; сопряжённое пространство; теорема о продолжении). Слабая сходимость в сопряжённом пространстве.




ТЕМА 34. Гильбертово пространство

Основные понятия; задача о наилучшем приближении и теорема об ортогональном дополнении; общий вид линейного функционала. Ортонормальные системы в гильбертовых пространствах. Процесс ортогонализации. Полнота и замкнутость. Теорема о разложении в ряд Фурье. Изоморфизм гильбертовых пространств.




ЛИТЕРАТУРА




Основная:
  1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Лань. Т.1-3, 2009.
  1. Кудрявцев Л.Д. Математический анализ. М.: Дрофа, Т.1-2, 2006.
  1. Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П.Демидовича М.: Аст, 2007.
  1. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Аст, 2007.
  1. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М.: ЮНИМЕДИАСТАЙЛ, 2002.
  1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Физматлит, 2009.
  1. Люстерник Л.А., Соболев В.И.. Элементы функционального анализа. М: Лань, 2009.
  1. Треногин В.А., Писаревский Б.М., Соболева Т.С. Задачи и упражнения по функциональному анализу. М: Физматлит, 2002.

Дополнительная:



  1. Стинрод Н., Чинн У. Первые понятия топологии. Геометрия отображений отрезков, кривых, окружностей и кругов. М: ЛКИ, 2007 г
  1. Берман Г.Н. Сборник задач по курсу математического анализа, М.: Профессия, 2005.
  1. Смирнов В.И. Курс высшей математики, М.: BHV, 2008.
  1. Степанов В.В. Курс дифференциальных уравнений, М.: Комкнига, 2006.
  1. Бронштейн И.Н., Семендяев К.А.. Справочник по математике для инженеров и учащихся втузов. М.: Лань, 2009.
  1. Шилов Г.Е. Курс дифференциального и интегрального исчисления. М.: Наука. Т.1-3, (любое издание).
  1. Шипачев В.С. Задачи по высшей математике. М.: Оникс. 2009.
  1. Шабат Б.В. Введение в комплексный анализ. Часть I. Функции одного переменного. М.: Лань, 2004.
  1. Шабат Б.В. Введение в комплексный анализ. Часть II. Функции нескольких переменных. М.: Лань, 2004.
  1. Садовничий В.А. Теория операторов. М: Дрофа, 2004.
  1. Канторович Л.В., Акилов Г.П. Функциональный анализ, Спб.: Невский диалект, 2004.
  1. Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа. М: «Наука», 1988, 384с.