Исследование математических моделей. 15

Вид материала

Исследование

Содержание Глава 1. Формы представления информационных моделей. Понятие модели. Предметные модели Модели информационные Глава 2. Информационные модели. Графические информационные модели. Табличные модели. Глава 3. Информационные модели на графах. Ориентированный граф. Взвешенный (размеченный) граф. Рассмотрим пример семантической сети Полученный граф напоминает ветвящийся куст, который «растёт сверху вниз»: верхние уровни имеют меньшие номера, нижние - большие. Глав 4. Моделирование и формализация. Глава 5. Разработка моделей и их исследование. Глава 6. Электронные таблицы и математическое моделирование. Глава 7. Исследование математических моделей. Подбор параметра Библиографический список.

Подобный материал:

• Исследование математических моделей, 9.9kb.
• План изучения дисциплины № п/п, 155.57kb.
• Шейчекова Марина Евгеньевна, 10А класс Научный Кулигина Анна Леонидовна, учитель информатики, 18.75kb.
• Лекции по дисциплине «Математическое моделирование» для студентов и магистрантов специальности, 21.92kb.
• Тематический план учебной дисциплины, 52.63kb.
• Лекция №8 Построение математических моделей технологических объектов и систем аналитическим, 98.99kb.
• Рабочая программа разработана в соответствии с государственными требованиями к минимуму, 189.13kb.
• Магистерская программа: Энергетика теплотехнологии (кафедра эвт); Форма обучения: очная, 55.97kb.
• Темы выпускных квалификационных работ кафедры «Экономический анализ» в 2010-2011, 71.48kb.
• Исследование операций построение, разработка и приложения математических моделей принятия, 149.21kb.

Оглавление.

Введение.

Вы когда – нибудь увлекались моделированием? Клеили модель самолёта? Возились с игрушечной железной дорогой? Быть может, даже запускали в небо настоящую модель ракеты? А не хотите ли создать модель звезды – например, нашего солнца?

Модель даёт нам недорогой и безопасный способ изучить некоторые свойства “оригинала”. Авиамодель копирует форму настоящего самолёта. Игрушечный поезд повторяет не только форму, но и движение реального состава. Модель ракеты использует реактивное движение – тот же принцип действия, что и в мощном космическом носителе.

Материалом, из которого они изготовлены, эти модели хотя бы отдалённо напоминают свои прототипы. Но как моделировать объект, для которого на Земле нет подходящих материалов? Как смоделировать Солнце, поверхность которого разогрета до 6000 градусов и в центре которого газ в четыре раза плотнее свинца и идут термоядерные реакции?

Существует лишь один материал, из которого можно построить такую модель: это числа. Указав температуру на поверхности и плотность в центре Солнца, мы уже создали очень простую его модель. Чтобы построить более точную, надо обратиться к основам физики звёзд.

Тема данного реферата “Исследование моделей на компьютере”.

Выбранная тема актуальна, т.к. информационное моделирование – это прикладной раздел информатики, связанный с самыми различными предметными областями: техникой, экономикой, естественными и общественными науками. Большинство разделов информатики имеют прямое отношение к моделированию.

При работе над темой была использована различная литература. Наиболее часто мы обращались к учебной литературе. Но использовались и публикации из периодических изданий и информация из электронных средств.

При написании работы была поставлена цель: научиться создавать различные математические модели и исследовать их поведение с помощью электронных таблиц. В процессе работы над поставленной целью необходимо было решить следующие задачи:

• Определить понятие модели и познакомится с основными типами информационных моделей.
  
• Научиться описывать модели на формальном языке.
  
• Рассмотреть математическую модель объекта или процесса, т.е. научиться строить модели с использованием математических понятий и формул.
  
• Строить компьютерные модели в среде электронных таблиц Exceel.
  

Работа кроме теоретической части имеет и практическую направленность. В данной работе описан вычислительный эксперимент в области биологии и разработан способ решение уравнений графическим методом с последующим уточнением параметров.

Глава 1.

Формы представления информационных моделей.

Понятие модели.

В своей деятельности научной, практической, художественной - человек очень часто использует модели, т.е. создаёт образ того объекта (процесса или явления), с которым ему приходится иметь дело.

К созданию моделей прибегают, когда исследуемый объект либо очень мал (модель атома), когда процесс протекает очень быстро (модели двигателя внутреннего сгорания) или очень медленно (геологические модели), исследование объекта может привести к его разрушению (модель самолёта) или создание модели очень дорого (архитектурный макет города).

Модель-это некоторое упрощённое подобие реального объекта.

Разные науки исследуют объекты и процессы под разным углом зрения и строят различные типы моделей. В физике изучают процессы взаимодействия и движения объектов, в химии - их внутреннее строение, в биологии - поведение живых организмов и т.д.

Разные объекты могут описываться одной моделью. Так, в механике различные материальные тела (от планеты до песчинки) могут рассматриваться как материальные точки.

Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.

Все модели можно разбить на два больших класса: модели предметные (материальные) и модели знаковые (информационные).

Предметные модели

Предметные модели воспроизводят геометрические, физические и др. свойства объектов в материальной форме. В процессе обучения мы используем такие модели: глобус (география), муляжи (биология), модели кристаллических решеток (химия) и др.

Модели информационные

Модели информационные представляют объекты и процессы в форме рисунков, схем, чертежей, таблиц, формул, текстов и т.д. В школе мы используем такие модели: рисунок цветка (ботаника), карта (география), формула (физика), блок-схема алгоритма (информатика), уравнение (математика) и т.д.

Ни какие объекты не может заменить сам объект. Но при решении конкретной задачи, когда нас интересует определённое свойство изучаемого объекта, модель оказывается полезным, а подчас и единственным инструментов исследования.

Глава 2.

Информационные модели.

Информационная модель объекта это его описание.

Метод описания может быть разным: словесным, математическим, графическим. Например, чертёж автомобиля является его графическим описанием, а стало быть, информационной моделью. Любая информационная модель содержит лишь существенные сведения об объекте с учётом той цели, для которой она создаётся.

Построение информационной модели предшествует анализ, задача которого: выделить существенные части и свойства объекта, связи между ними.

Информационные модели одного и того же объекта, предназначенные для разных целей, могут быть совершенно разными. Например, в личной карточке работника предприятия, которая хранится в отделе кадров, о нём имеются следующие сведения: Ф.И.О., пол, год рождения, место рождения, национальность, адрес проживания, образование, семейное положение. В медицинскую карточку того же самого человека занесены следующие данные о нём: Ф.И.О., пол, год рождения, группа крови, вес, рост, хроническое заболевание. В обществе охотников, членом которого является этот человек, о нём хранится другой набор сведений. Как видим, разное назначение-разные информационные модели.

Графические информационные модели.

Информационной моделью можно назвать карту местности. Во-первых, карта-это графическая информация. Во- вторых, она приближённо описывает местность, не включая лишних деталей.

Другими знакомыми нам примерами графических информационных моделей являются чертежи, схемы, графики, диаграммы, рисунки и т.д.

Чертёж должен быть очень точным, на нём указываются все необходимые размеры.

Графики являются информационными моделями, которые в наглядной форме представляют числовые данные: в математике это графики функций, в экономике отражение статистических данных и т.д.




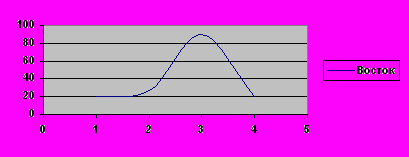
Рис.1
Диаграммы также являются информационными моделями, представляющими числовые данные. Диаграммы различных типов применяются, прежде всего, для наглядного представления статистических данных (р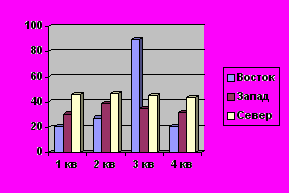ис.2).

Рис.2


На протяжении своей истории человечество использовало различные способы и инструменты для создания информационных моделей. Эти способы постоянно совершенствовались, как первые графические информационные модели создавались в форме наскальных рисунков. В настоящее время графические модели обычно строятся с использованием современных компьютерных технологий.

Табличные модели.

Для представления информационных моделей широко используются таблицы.

При составлении таблицы в неё включается лишь та информация, которая интересует пользователя.

Таблица может отражать некоторый процесс, происходящий во времени. Такие таблицы будем называть таблицами типа «объект-свойство». В этих таблицах одна строка содержит информацию об одном объекте или одном событии. Столбцы - отдельная характеристика (свойства) объекта или события.

Другим распространенным типом таблиц являются таблицы, отражающие взаимосвязи между разными объектами. Будем называть их таблицами типа «объект-объект».

Числовая прямоугольная таблица называется матрицей. Если матрица содержит только нули и единицы, то она называется двоичной матрицей.

Двоичная матрица отражает качественный характер связей между объектами.

С помощью таблицы могут быть выражены как статистический, так и динамические информационные модели. Например, рассмотрим компьютер с точки зрения стоимости его цены во времени.

Построим статистическую информационную модель, отражающую стоимость отдельных устройств компьютера. Статическая информационная модель «цена устройств компьютера» может быть представлена в форме таблицы. В первом столбце таблицы пусть содержится перечень объектов (устройств), входящих в состав компьютера, а во втором их цена.


Цена устройств компьютера.

Наименование	Цена (в у, е.)
Системная плата	80
Процессор Cameron (400мгц)	70
Память 32 Мб	45
Жёсткий диск 10 Гб	130
Дисковод 3,5	14
Видеоплата 8 Мб	30
Монитор 15	200
Звуковая карта 16 бит	30
Дисковод CD-ROM*48	50
Корпус	25
Клавиатура	10
Мышь	5

В табличной информационной модели объекты или их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной таблицы.

Табличные информационные модели проще всего строить и исследовать на компьютере с помощью электронных таблиц и систем уравнения базами данных.

Таким образом, табличные информационные модели находят широкое применение в различных сферах человеческой деятельности с помощью табличных моделей можно систематизировать различную информацию и таблицы упрощают работу с ней

Глава 3.

Информационные модели на графах.

Граф – это средство для наглядного представления состава и структуры системы. Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Граф состоит из вершин, связанных дугами или рёбрами. Вершины могут быть изображены кругами, овалами, точками, прямоугольниками и пр. Связи между вершинами изображаются линиями. Если линия направленная

(т. е. со стрелкой), то она называется дугой, если не направленная (без стрелки), то ребром. Принято считать, что одно ребро заменяет две дуги, направленные в противоположные стороны. Граф, в котором все линии направленные, называется ориентированным графом. Две вершины, соединённые дугой или ребром, называется смежными.

В случае представления информации о составе структуре системы в виде графа компоненты системы изображаются вершинами, а связи между ними – линиями (дугами и рёбрами).

Ориентированный граф.

Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую концом. Граф, все рёбра которого ориентированны, называется ориентированным графом. Одна и та же вершина ориентированного графа может служить началом для одних рёбер и концом для других (рис.3).


Индустриальный

Пермь

Дзержинский





Школа 122

Школа 3



Лукина

Павлов


Васин

Луценко

Орлова



Рис.3

Взвешенный (размеченный) граф.

Это граф, в котором с вершинами или линиями связанна некоторая информация. Эта информация называется весом вершины или линиями. Чаще всего вес задаётся в виде надписи на вершине или линии, но возможны и другие способы: форма и цвет вершины, толщина, цвет и тип линии (например, сплошная или пунктирная).

Вес позволяет отобразить на графе не только структуру системы, но и различные свойства компонентов и связей, количественные характеристики и пр.


Рассмотрим пример семантической сети, представленной в виде графа (рис.5). Нетрудно понять смысл заключённой в ней информации.





имеет свойство







имеет свойство


имеет часть

является


является

имеет св - во









имеют св - во













Имеет часть







Рис.5


Н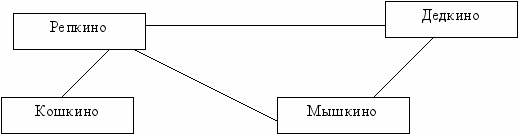а рисунке 6 изображён взвешенный граф, представляющий информацию о дорогах между четырьмя деревнями. Веса вершин - название деревень, веса линий - длина дорог в километрах. И те, и другие задаются надписями.


14


4 5 12


Рис.6

Дерево

Это граф, предназначенный для отображения таких связей между объектами как вложенность, подчинённость, наследование и т.д. и т.п.

Строится он следующим образом. Сначала рисуем «главную» вершину, которая не зависит ни от одной другой вершины. Эта вершина называется корнем дерева и является единственной вершиной «1- уровня». Далее добавляем вершины «2- уровня». Их может быть сколько угодно, и все они обязательно связаны с корнем- вершиной 1-го уровня, но не связаны между собой. На следующем шаге добавим вершины 3-го уровня. Каждая из них будет связана ровно с одной вершиной 2-го уровня и не связана ни с одной другой вершиной. К любой вершине 2-го уровня может быть подсоединено сколько угодно вершин 3-го уровня (в том числе, ни одной). Следующий шаг- добавка вершин 4-го уровня, каждая из которых будет связана ровно с одной вершиной 3-го уровня и не связана больше ни с чем. И так далее. На каждом шаге добавляем вершины очередного уровня, каждая из которых будет связана ровно с одной вершиной предыдущего уровня и не будет иметь никаких иных связей.

Полученный граф напоминает ветвящийся куст, который «растёт сверху вниз»: верхние уровни имеют меньшие номера, нижние - большие.

Сделаем вывод. В последнее время графы и связанные с ним и методы исследований органически пронизывают на разных уровнях едва ли не всю современную математику. Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, математической лингвистики, экономике, биологии, медицине. Широкое применение находят графы в программировании, теории конечных автоматов, электронике, в решении вероятных и комбинированных задач.

Глав 4.

Моделирование и формализация.

Естественные языки используются для создания текстовых описательных информационных моделей. Например, такой литературный жанр, как басня или притча, имеет непосредственное отношение к понятию модели, поскольку смысл этого жанра состоит в переносе реальных отношений между людьми на отношения между животными, между вымышленными персонажами и пр. Более того, всякое литературное произведение может рассматриваться как модель, ибо фокусирует внимание читателя на определённых сторонах человеческой жизни.

В истории науки также известны многочисленные текстовые информационные модели, например, гелиоцентрическая модель мира, которую предложил Коперник, формулировалась следующим образом:

• не Солнце движется вокруг Земли, а, наоборот, Земля вращается вокруг своей оси и вокруг Солнца;
  
• орбиты всех небесных тел проходят вокруг Солнца.
  

С помощью формальных языков строятся информационные модели определённого типа – формально-логические модели. Например, с помощью алгебры логики можно построить логические модели сумматора и триггера.

Процесс построения информационных моделей с помощью формальных языков называется формализацией.

Одним из наиболее распространённых формальных языков является алгебраический язык формул в математике, который позволяет описывать функциональные зависимости между величинами. Модели, построенные с использованием математических понятий и формул, называется математическими моделями. Так, чтобы формализовать гелиоцентрическую модель, необходимо воспользоваться законами Ньютона и законом всемирного тяготения.

В школьном курсе физики рассматривается много разнообразных уравнений, которые представляют собой математические модели изучаемых явлений или процессов. Если вас просят решить физическую задачу, то вы начинаете с поиска подходящего уравнения, т.е. с построения математической модели, которая отвечает условиям вашей задачи.

В процессе познания окружающего мира человечество постоянно использует моделирование и формализацию. При изучении нового объекта сначала обычно строится его описательная модель, затем она формализуется, т.е. выражается с использованием математических формул, геометрических объектов и т.д.

Глава 5.

Разработка моделей и их исследование.

Процесс разработки моделей и их исследование на компьютере можно разделить на несколько основных этапов.

На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные, с точки зрения целей проводимого исследования, параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создаётся формализованная модель, то есть описательная информационная модель записывается с помощью какого – либо формального языка. В такой модели с помощью формул, уравнений, неравенств и так далее фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, то есть выразить её на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

• построение алгоритма решения задачи и его кодирование на одном из языков программирования;
  
• построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и так далее).
  

Четвёртый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, её нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например, в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов, можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности.

В данной работе построение компьютерной модели будет происходить с использованием электронных таблиц Excel.

Глава 6.

Электронные таблицы и математическое моделирование.

Чаще всего электронные таблицы используются для получения расчётных ведомостей, смет, справок, списков, т.е. в области делопроизводства.

Однако ЭТ могут оказаться полезными и для научных целей. С помощью электронных таблиц можно проводить вычислительные эксперименты.

В результате вычислительного эксперимента можно получить прогноз поведения исследуемой системы; выяснить вопрос о том, как изменение одних характеристик системы отразится на других.

Рассмотрим пример такого вычислительного эксперимента.

Пример 1: Учёные установили, что прирост числа какого-либо вида живых организмов за счёт рождаемости прямо пропорционален их количеству, а убыль за счёт смертности прямо пропорциональна квадрату от их количества. Этот закон известен под названием закона Мальтуса. В одном хозяйстве собираются разводить карпов. Прежде, чем запустить мальков в пруд, решили провести расчёт. Согласно закону Мальтуса изменение числа рыб за один год вычисляется по формуле N=kN-gN² .

Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоёма, наличие корма) k=1, g=0,001.

Если первоначально установлено в пруд запущено N₀ рыб, то из закона следует, что количество карпов через год будет таким:N₁=N₀+(kN₀-gN₀²)

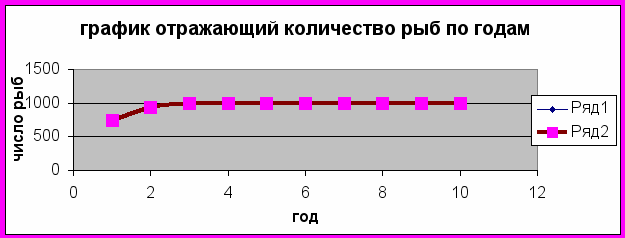
Запустим 1500 карпов и выполним расчёты

Расчёт числа рыб в пруду с интервалом через год.
k-коэффициент прироста
g-коэффициент смертности
N0-первоночально запущенно рыб
N=kN-gN2		N1=N0+(kN0-gN02)
k=	1	g=	0,001	N0=	1500
год		число рыб
0		1500
1		750
2		938
3		996
4		1 000
5		1 000
6		1 000
7		1 000
8		1 000
9		1 000
10		1 000

Теперь запустим 100 карпов и снова выполним расчёт.

k=	1	g=	0,001	N0=	100
год		число рыб
0		100
1		190
2		344
3		570
4		815
5		966
6		999
7		1 000
8		1 000
9		1 000
10		1 000

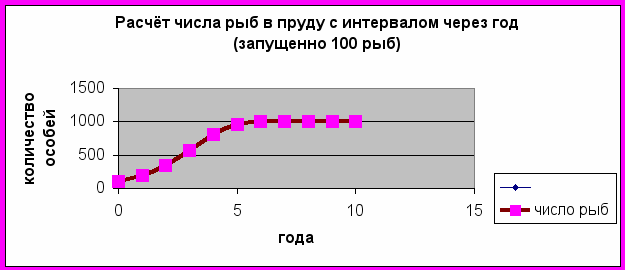
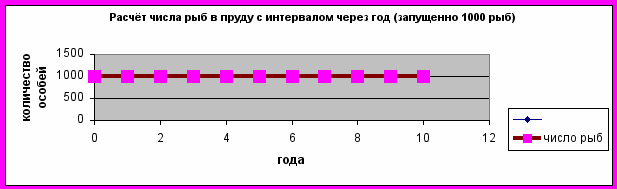
Не правда ли, удивительные результаты? Из приведённых таблиц следует, что невозможно иметь в пруду больше 1000 карпов. Если начальное число рыб меньше 1000, то оно постепенно будет расти до 1000 штук и далее не меняется. Если сразу запустить 1000 рыб, то это количество останется неизменным и в последующие годы. Даже если запустить сначала 1500 рыб, то через год их численность в два раза сократится, а затем всё равно дойдёт до 1000. Если же запустить в пруд 2000 рыб, то через год все они вымрут.

k=	1	g=	0,001	N0=	1000
год		число рыб
0		1 000
1		1 000
2		1 000
3		1 000
4		1 000
5		1 000
6		1 000
7		1 000
8		1 000
9		1 000
10		1 000

k=	1	g=	0,001	N0=	2000
год		число рыб
0		2 000
1		0
2		0
3		0
4		0
5		0
6		0
7		0
8		0
9		0
10		0

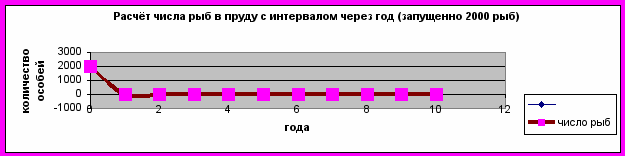
Из полученных результатов рыбоводы могут сделать практические выводы. Приведённые выше таблицы автоматически получались после изменений значения всего лишь в одной ячейке F1.

Глава 7.

Исследование математических моделей.

Рассмотрим, как с помощью математического моделирования можно решать математические задачи.

Пример 2: решить графически уравнение x³/10=sinx

1.Ввести формулы функции и заполнить таблицу значений функций на интервале от –2,5 до 2,5 с шагом 0,5.

2.Ввести команду [Вставка-Диаграмма…].

На панелях Автоформат диаграммы выбрать Ряд данных в: Строки и тип диаграммы Линии с символами.

Будут построены два графика функций, координаты их точек пересечения и будут корнями уравнения: x₁≈-2, x₂≈0, x₃≈2

Таблица значений функций.
X	-2,5	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	2,5
Y1=Sin(X)	-0,60	-0,91	-1,00	-0,84	-0,48	0,00	0,48	0,84	1,00	0,91	0,60
Y2=X3/10	-1,56	-0,80	-0,34	-0,10	-0,01	0,00	0,01	0,10	0,34	0,80	1,56

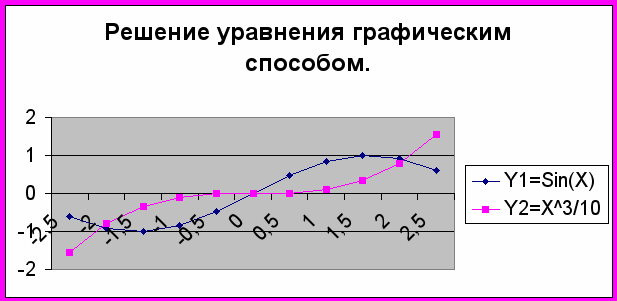
3. Определим более точные координаты точек пересечения данных графиков.

Метод Подбор параметра используется при поиске значения аргумента функции, который обеспечивает требуемое значение функции. При подборе параметра изменяется значение в ячейке аргумента функции до тех пор, пока значение в ячейке самой функции не возвращает нужный результат. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы.

1. Ввести формулы функций и заполнить таблицу значений функций на интервале от-2,5 до 2,5 с шагом 0,5. Установить точность представления чисел в ячейках с точностью 4 знака после запятой.
   
2. Построить графики функций. По графикам грубо приближённо можно определить, что уравнение имеет корни x₁≈-2, x₂≈0, x₃≈2.
   
3. Выделить ячейку, содержащую значение функции наиболее близкое к нулю, например, $K$3. Ввести команду [Сервис-Подбор параметра…].
   
4. На панели Подбор параметра в поле Конечное значение ввести требуемое значение функции (в данном случае 0).
   

В поле изменяемая ячейка ввести адрес ячейки $K$3, в которой будет производиться подбор значения аргумента.

5. На панели Результат подбора параметра будет выведена информация о величине подбираемого и подобранного значения.
   
6. В ячейке аргумента К2 появится подобранное значение 2,0648. Повторить подбор параметра для ячейки значения функции С3. В ячейке аргумента С2 появится подобранное значение –2,0648.
   

x	-2,5000	-2,0648	-1,5648	-1,0648	-0,5000	0,0000	0,5000	1,0000	1,5000	2,0648	2,5648
Y=x3/10-Sin(x)	-0,9640	0,0001	0,6168	0,7540	0,4669	0,0000	-0,4669	-0,7415	-0,6600	-0,0001	1,1418

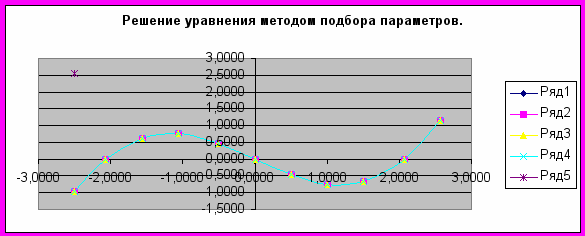
Таким образом, корни уравнения с точностью до четырёх знаков после запятой найдены: x₁≈-2.0648, x₂≈0.0000, x₃≈2.0648.

Ответ: решением уравнения x³/10=Sinx являются корни x₁≈-2.0648, x₂≈0.0000, x₃≈2.0648.

Заключение.

1. Тема, освещённая нами актуальна т.к. понятие модели – фундаментальное понятие информатики. Оно проходит через весь курс информатики, изучаемой в школе.
   
2. В процессе познания окружающего мира человечество постоянно использует моделирование и формализацию. Очень часто формализованная модель выражается с помощью математических формул, т.е. математическая модель – одна из наиболее используемых.
   
3. Основной инструмент при создании и исследовании моделей – компьютер. Прикладные программы помогают быстро и надёжно исследовать созданные модели и представлять наглядный результат.
   

Библиографический список.

1. Вершинин О.Е. За страницами учебника информатики: Кн. Для учащихся 10-11 кл. сред. Шк. – М.: Просвещение, 1991.
   
2. Журин А.А. Excel 2000. Для школьников и начинающих пользователей. – М.: “АКВАРИУМ ЛТД”, К.: ГИППВ, - 2000.
   
3. Информатика. Задачник – практикум в 2т./Под ред. И. Г. Семакина, Е.К. Хеннера: Том 1. – М.: Лаборатория Базовых Знаний, 2001.
   
4. Информатика. Задачник – практикум в 2т./Под ред. И.Г. Семакина, Е.К.Хеннера: Том 2. – М.: Лаборатория Базовых Знаний, 2001.
   
5. Информатика. Базовый курс. 7-9 классы. – М.: Лаборатория Базовых Знаний, 2001.
   
6. Угринович Н.Д. Информатика и информационные технологии. Учебное пособие для 10-11 классов. Углублённый курс. – М.: Лаборатория Базовых Знаний, 2000.
   
7. Угринович Н.Д. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений / Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова. – М.: Бином. Лаборатория Знаний, 2002.
   
8. Газета об информационных технологиях “Школьная компьютера”.№13. 11 ноября 2003.
   

Приложения.