Математические методы в психологии
| Вид материала | Рабочая учебная программа |
- Учебно-методический комплекс по дисциплине «Математические методы в психологии», 424.07kb.
- Курса «Математические методы в психологии». Данный курс реализуется в рамках подготовки, 107.45kb.
- Математические методы в психологии для направления подготовки бакалавра по направлению, 33.43kb.
- Примерная программа дисциплины "Математические методы финансового анализа", 464.29kb.
- Рабочей программы учебной дисциплины математические методы и модели в экономике уровень, 37.32kb.
- Многоуровневые модели зависимости экономического роста от инвестиций: эконометрический, 321.8kb.
- Математические методы принятия управленческих решений в туризме Мордовченков, 94.86kb.
- Инструментарий анализа качества ассортимента и оценки рейтингов товаров предприятий, 286.28kb.
- Рабочая программа дисциплины «экономико-математические методы и модели», 129.59kb.
- Учебно-методический комплекс опд. Ф. 11 «Математические методы в психологии» (индекс), 567.2kb.
Специальность «Психология»
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ
Требования ГОСТ к содержанию курса
Рабочая учебная программа
Цели и задачи курса
Тематический план курса
Содержание программы по разделам
Темы семинаров
Контрольные вопросы к зачету
Дополнительная информация.
Требования ГОСТ к содержанию курса
Измерение в психологии; типы шкал; представление данных; описательная статистика; меры связи; метрика; методы одномерной и многомерной прикладной статистики; многомерное шкалирование; многомерный анализ данных (факторный, кластерный); дисперсионный анализ; анализ данных на компьютере; статистические пакеты; приближенные вычисления; возможности и ограничения конкретных компьютерных методов обработки данных; стандарты обработки данных; нормативы представления результатов анализа данных в научной психологии; методы математического моделирования; модели индивидуального и группового поведения, моделирование когнитивных процессов и структур, проблема искусственного интеллекта.
Программа дисциплины «Математические методы в психологии»
Составлена старшим преподавателем Е.Б.Орловой, утверждена на заседании кафедры математического моделирования 28.01.2005
Цели и задачи курса
Обеспечить изучение некоторых разделов математической статистики и статистических методов; ознакомить студентов с возможностью применения ПЭВМ для обработки психологических экспериментов; подготовить студентов к самостоятельному овладению необходимыми для дальнейшей работы математическими знаниями.
В результате изучения курса студент должен уметь
Создавать, открывать, сохранять и закрывать файлы в системах Maple V, Excel, Statistica.
- Создавать программы для первичной обработки данных в пакете Maple V.
- Заносить формулы в ячейки (с мастером функций или без него) в приложении Excel.
- Производить операции с переменными и случаями (добавлять, удалять, переименовывать) в системе Statistica.
- Вносить формулы для решения вероятностных задач (используя основные виды распределений случайных величин или «вероятностный калькулятор») в системе Statistica.
- Классифицировать задачи и определять методы их обработки.
- Производить первичный анализ данных (аналитически, графически).
- Формулировать статистические гипотезы, находить эмпирическое значение критерия, использовать таблицы критических значений, пользоваться правилами принятия или отклонения гипотез.
- Интерпретировать полученный результат.
Тематический план курса
| № | Наименование темы | Лекции (час.) | Практические занятия (час.) | Лабораторные работы (час.) |
| 1. | Начальные понятия прикладной статистики | 2 | 4 | |
| 2. | Первичный анализ данных в системах Statistica, Maple V, Excel | 2 | 6 | 4 |
| 3. | Основные понятия, используемые в математической обработке психологических данных | 2 | 6 | |
| 4. | Выявление различий в уровне исследуемого признака | 6 | 10 | 7 |
| 5. | Оценка достоверности сдвига в значениях исследуемого признака | 5 | 10 | 6 |
| | Итого | 17 | 34 | 17 |
Содержание программы курса по темам
| СЕМЕСТР 4 | |
| Тема 1 | Начальные понятия прикладной статистики. Генеральная и выборочная совокупности, вариационный ряд, статистическое распределение выборки, функция распределения. Характеристики вариационного ряда: выборочное среднее, выборочная дисперсия, исправленная дисперсия, стандартное отклонение, медиана, мода, размах, квартили. |
| Тема 2 | Первичный анализ данных: Математическая система Maple V. Графические возможности пакета Maple V Первичный анализ данных при помощи приложения Excel. Система Statistica: операции с файлами, рабочее окно системы. Операции с переменными и случаями. Первичный анализ данных в системе Statistica. Решение вероятностных задач в системе (распределения: биномиальное, Пуассона, нормальное). |
| Тема 3 | Основные понятия, используемые в математической обработке психологических данных. Признаки и переменные, шкалы измерения: номинативная, порядковая, интервальная, равных отношений. Статистические гипотезы: нулевая и альтернативная, направленная и ненаправленная; статистические критерии: параметрические и непараметрические, их возможности и ограничения. Уровни статистической значимости, ошибки первого и второго родов, правила отклонения и принятия гипотез; мощность критериев; классификация задач и методов их решения. |
| Тема 4 | Выявление различий в уровне исследуемого признака. Критерий Q Розенбаума. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Критерий U Манна-Уитни. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Применение возможностей компьютера при решении задач. Критерий H Крускала-Уоллиса. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Компьютерный вариант обработки. Критерий S тенденций Джонкира. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Компьютерный вариант обработки. Многофункциональный критерий 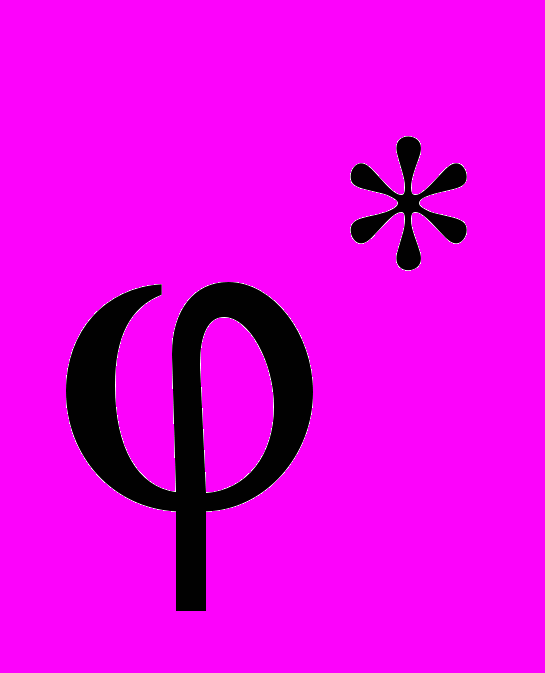 - угловое преобразование Фишера (в применении к данной задаче). Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Использование приложения Excel для нахождения эмпирического значения критерия. - угловое преобразование Фишера (в применении к данной задаче). Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Использование приложения Excel для нахождения эмпирического значения критерия. |
| Тема 5 | Оценка достоверности сдвига в значениях исследуемого признака. Обоснование задачи исследования изменений. Критерий G знаков. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Компьютерный вариант обработки. Критерий Т Уилкоксона. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Применение системы Statistica для обработки эксперимента с помощью критерия Уилкоксона. Критерий 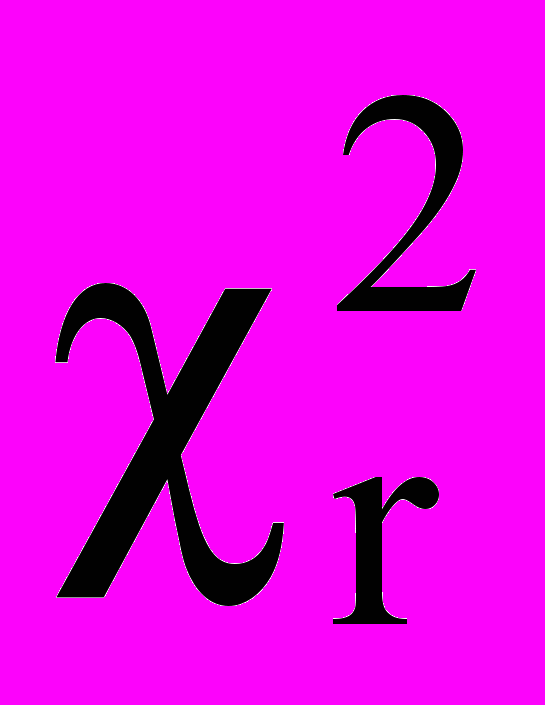 Фридмана. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Компьютерный вариант обработки. L – критерий тенденций Пейджа. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Многофункциональный критерий Фридмана. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Компьютерный вариант обработки. L – критерий тенденций Пейджа. Ограничения по применению, графическое представление, формулировка гипотез, алгоритм решения, правило принятия гипотез. Многофункциональный критерий 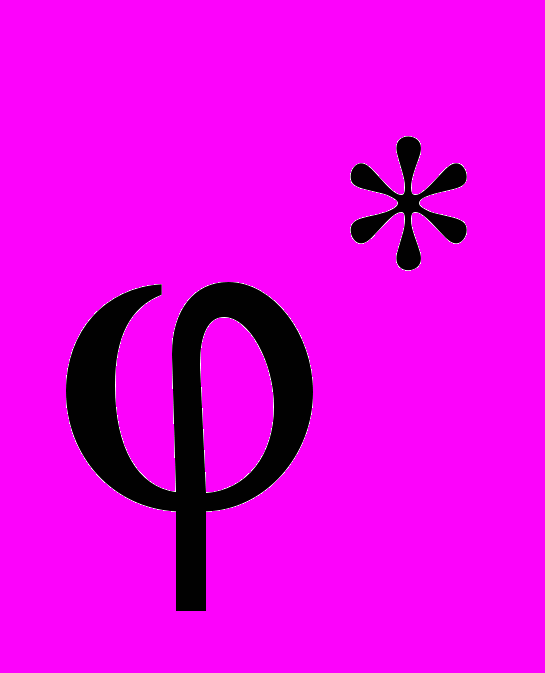 - угловое преобразование Фишера (в применении к данной задаче). Применение приложения Excel. - угловое преобразование Фишера (в применении к данной задаче). Применение приложения Excel. |
Литература:
- Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. – М.: МГУ, 1975.
- Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: «Речь», 2000.
- Суходольский Г.В. Основы математической статистики для психологов. Л.: ЛГУ, 1972.
- Тюрин Ю.Н. Непараметрические методы статистики. М.: Знание, 1978.
- Паповян С.С. Математические методы в социальной психологии. М.: Наука, 1983.
