Математические методы принятия управленческих решений в туризме Мордовченков Н. В

Вид материала

Содержание

Рис. 1. Использование ЭМММ при принятии управленческого решения.
Сетевые модели
Аналитические методы
Метод математического программирования
Матричный метод
Теория игр.
Алгоритм решения матричной игры [3]
Найти: оптимальные смешанные стратегии игроков
Решение: составим систему неравенств

Подобный материал:

Математические методы принятия управленческих решений в туризме

Мордовченков Н.В.,

доктор экономических наук, профессор, зам. директора по научной работе СГУТ и КД, г.Н.Новгород

Морозова И.Е.,

студентка СГУТ и КД

Современные математические методы и модели широко распространены и успешно используются в следующей трактовке:

математические методы в принятии решений;
методы исследования операций;
экономико-математические методы;
методы экономической кибернетики;
методы оптимального управления,
прикладная математика в экономике и организации туристско-экскурсионных маршрутов.

В ряде научных исследований они рассматриваются в различных сочетаниях, с учетом степени густоты их исследования при формализации прикладных моделей.

В экономико-математических методах применяется весь арсенал математики, математической статистики, векторной алгебры и математической логики, значительный «вклад» при решении эконометрических задач вносит вычислительная математика, теория алгоритмов и апироксимации.

Эконометрические методы и модели (ЭМММ) – это логистический системный подход при решении инфраструктурных проблем менеджмента, что структурно можно изобразить в виде графической модели (рис.1):

Рис. 1. Использование ЭМММ при принятии управленческого решения.

Линейное программирование.

Широкое применение в решении экономтрических задач нашло при решении транспортных задач, в том числе в туризме, связанных с ограничениями (по ресурсам, времени, рабочей силе, энергии, финансам, материалам) и при достижении функции, цели, например, максимума прибыли. При этом значимым является линейность функциональных соотношений в математической модели. Алгоритм решений заключается в использовании последовательных хрестоматийных шагов.

При формализации стохастических моделей результаты представляют из себя вероятностный процесс и включает в себя некоторые риски, неопределенность и возможность наличия альтернативных решений.

При решении традиционных задач управления запасами необходимо разработать специальные сценарии системного анализа проблем ресурсов, что характерно для большинства туристических фирм. Этот подход является весьма полезным в управлении издержками в инфраструктуре малого бизнеса.

Сетевые модели являются удобной формой в системе действий для их анализа. Некоторые процедуры формируют многоступенчатую последовательность итераций.

Так в менеджменте туризма наибольшее значение, в частности, уделяется:

- имитационным моделям;

- линейному программированию;

- теории графов;

- сетевым моделям;

- теории массового обслуживания;

- функциям замещения;

- интегральному исчислению и программированию.

Аналитические методы оказывают содействие работе руководителя или специалиста путём создания аналитических зависимостей. Происходит процесс соотнесения между детерминируемой возможностью выполнения задач и её результатами в виде графической и табличной модели. «Заплати налоги – спи спокойно».

При функционировании туристского бизнеса встречается множество типовых зависимостей объективного характера: зависимость между спросом и предложением, неудовлетворенного спроса производительности и интенсивности труда от квалификации и компетентности персонала, стиля управления от характера деятельности компании, качества УР от полноты и ценности информации и др. Каждый руководитель имеет некоторый набор таких зависимостей, выработанных интуитивно в течение ряда лет или полученных в результате обучения. Многие эффективные зависимости так и остаются для некоторых руководителей «за кадром». Зачастую приходится осуществлять поиск эффективных зависимостей методом проб и ошибок, нерационально используя ограниченные ресурсы в условиях дефицита времени. В условиях постиндустриальной экономики реализация информационного ресурса всё увереннее становится источником формирования эффективного бизнеса.

Основу этих методов составляют: теория вероятностей, теория марковских процессов, теория массового обслуживания.

При использовании cтатистических методов опираются, как правило, на прошлый позитивный опыт ряда организаций в конкретной сфере туристских услуг для разработки и реализации УР собственной компании. Эти методы реализуются на основе сбора, обработки и анализа статистических данных с использованием финансово-экономического анализа, а также с применением информационных компьютерных РС-технологий. К этим методам относятся последовательный анализ и метод статистических испытаний.

Метод математического программирования позволяет менеджеру-аналитику рациональный вариант решения по выбранным критериям: минимум времени, максимум цены, качества и др. (рис. 2)

Рис. 2. Схема реализации метода математического программирования

Наиболее популярна техника линейного программирования. Она используется для решения задач, связанных с ограничениями (по ресурсам, времени, рабочей силе, энергии, финансам, материалам) и с целевой функцией типа максимизации прибыли. Существенным является линейность функциональных соотношений в математической модели. Конкретная техника решений состоит в использовании алгоритма последовательных шагов (т.е. программы). Работник, разрабатывающий решения, вводит в компьютер набор ситуаций, подлежащих изменению в соответствии с целью, а также критерии. Компьютер на базе математических соотношений либо разрабатывает новое решение, либо выбирает подходящее из набора альтернативных решений. Метод хорошо работает только при наличии четко сформулированной цели.

Матричный метод используется при выборе эффективного управленческого решения на альтернативной основе по системе компромисса признаков (критериев), достигнутых заинтересованными сторонами. Возможный компромисс достигается как правило между двумя, тремя или более заинтересованными сторонами.

Матричный метод – это объективный метод в принятии управленческих решений. Он применяется при возникновении повторяющихся или сходных ситуаций. При этом в базе данных должен присутствовать спектр альтернативных решений и различных критериев.

В задачу руководителя входит согласование значений критериальных параметров и их ранжирование в системе приоритетов.[2]

Теория игр.

В институциональной экономике встречаются такие явления и процессы, участники которых имеют несовпадающие, а то и прямо противоположные интересы. При этом для достижения своих целей участники располагают различными возможностями и путями. В рамках прикладных математических задач такие события называют конфликтными и просто – конфликтами. Ситуацию также можно трактовать как конфликтную, когда имеются многосторонние интересы одной стороны, т.е. когда требования, предъявляемые к какому-либо объекту или процессу, являются противоречивыми.

Таким образом, наличие неопределенностей может быть обусловлено различными аспектами. Формализация конфликтной ситуации представляет собой математическую модель, называемую игрой, а участников конфликта - игроками. Оптимальное поведение игроков в различных играх изучается теорией игр. В настоящее время она развилась в самостоятельную область теории исследования операций, представляющую собой теоретическую основу методов разработки алгоритмов управления различными системами, функционирующими в условиях противодействия со стороны некоторой не вполне известной системы. Предполагается, что противоборствующая система действует разумно, оптимизируя свое поведение в своих интересах.

В условиях конфликта стремление сторон скрыть свои действия порождает неопределенность. В то же время, наоборот, неопределенность при принятии решений (например, на основе недостаточных данных) может интерпретироваться как конфликт принимающего решения субъекта с другими субъектами (фиктивным игроком или природой).

Теория игр может также рассматриваться как теория принятия оптимальных решений в условиях неопределенности.

Рассмотрим простейшую игровую модель. Пусть у игрока «А» имеется m вариантов действий, а у игрока «В» - n вариантов. Такая конечная игра называется игрой m

n . Обозначим варианты действий игрока «А» (условимся называть его «нашей стороной») через A₁, A₂ ..., А_m, а варианты действий игрока «В» (противника) – В₁ В₂, ..., В_n. Пусть каждый игрок выбрал по варианту действий: А_i и В_j, тогда результат игры будет оцениваться величиной d_ij. Если игра будет содержать еще и случайные ходы, то выигрыш также будет величиной случайной и оценкой ожидаемого выигрыша будет его среднее значение (математическое ожидание). Значения выигрышей (или их математических ожиданий), зависящих от пар стратегий, можно записать в виде таблицы. Условимся считать, что строки матрицы соответствуют нашим стратегиям, а столбцы - стратегиям противника. Такая таблица называется платежной матрицей или просто матрицей игры (см. рис. 3). Отсюда и название такого класса игр - матричные.

«B» «A»	B₁	B₂	…	B_n
A₁	d₁₁	d₁₂	…	d_1n
A₂	d₂₁	d₂₂	…	d_2n
…	…	…	…
A_m	d_m1	d_m2	…	d_mn

Рис.3. Платежная матрица

Цель теории игр - выработка рекомендаций по рациональному образу действий каждого из противников в ходе конфликтной ситуации, т.е. определение оптимальной стратегии каждого из них.

Алгоритм решения матричной игры [3]

Дано: конечная матричная игра размерности т п , заданная платежной матрицей (см. рис. 3).

Найти: оптимальные смешанные стратегии игроков

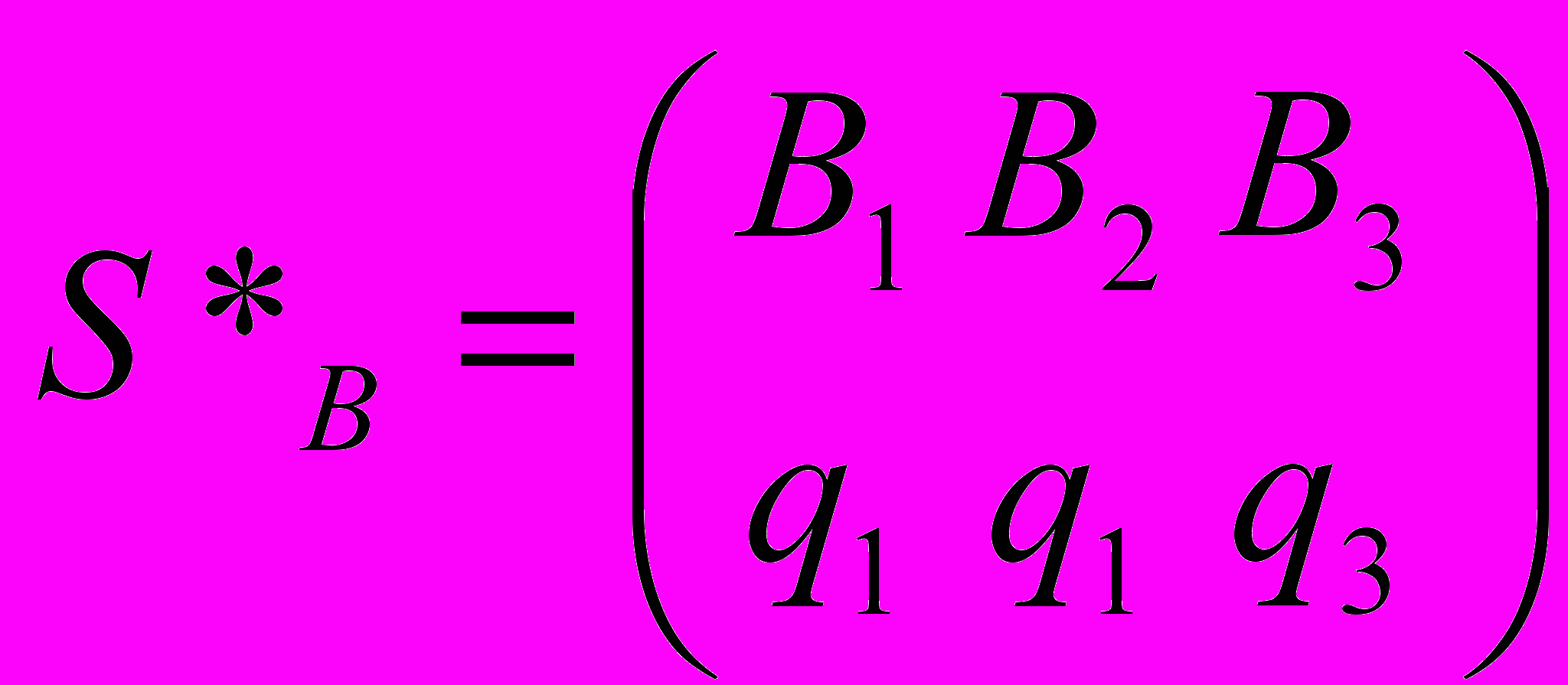
Условие: оптимальная стратегия игрока «А» должна обеспечивать выигрыш не менее некоторого значения V при любой стратегии игрока «В».

Решение: составим систему неравенств

Разделим неравенства на V (V>0) и обозначим:

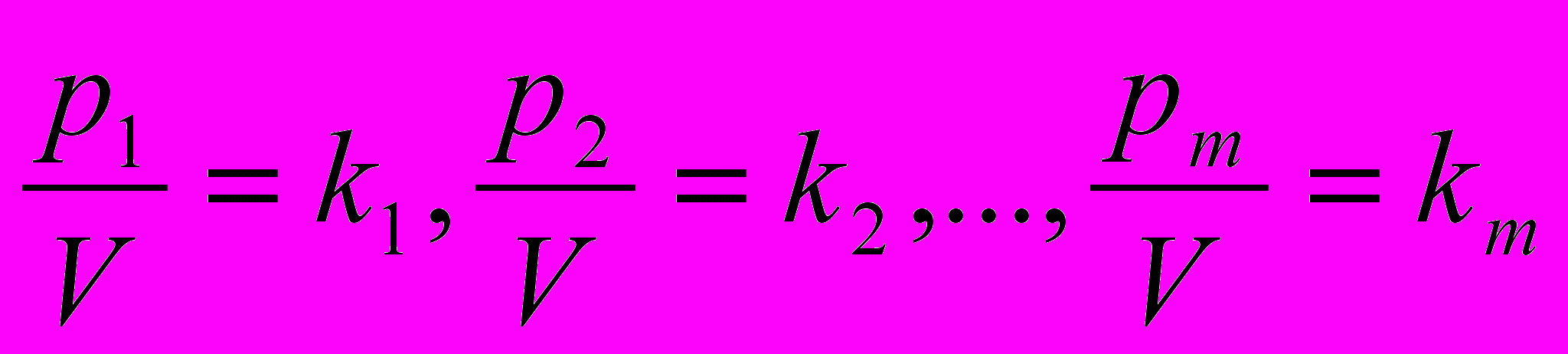
Так как вероятности p_i это неотрицательные величины

(

>0 ), a V - положительное число, то переменные k₁,k₂,...,k_m будут неотрицательными числами.

Тогда система неравенств примет следующий вид:

k₁d₁ +k₂d₂ +... + k_md_m1 1,

k₁d₂ +k₂d₂ +... + k_md_m₂ 1,

…

k₁d₁_n +k₂d₂_n +... + k_md_m 1,

Так как

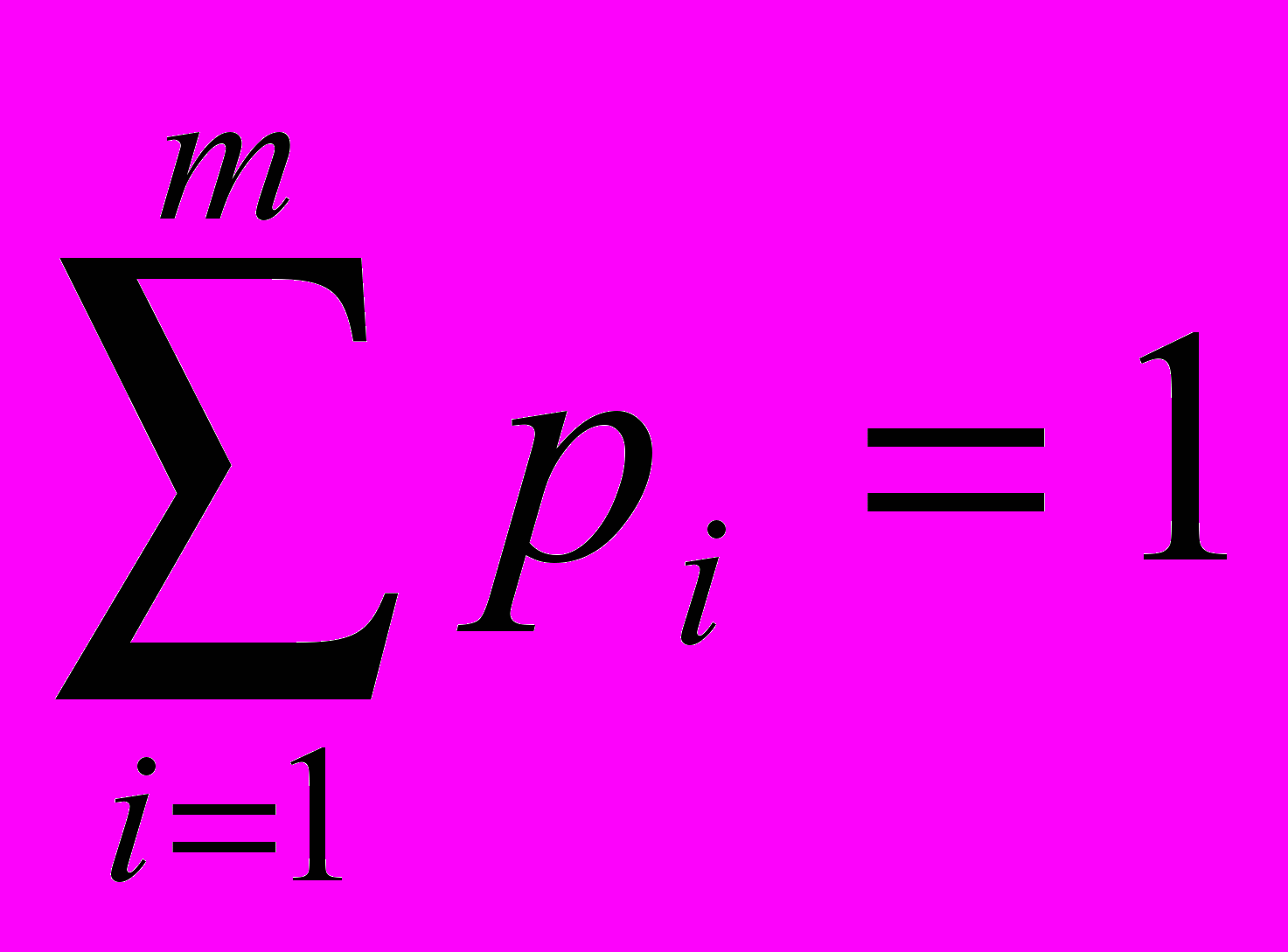, то

.

По условию задачи величина V должна быть максимальной, значит, величина

должна быть минимальной и, следовательно, необходимо определить величины k₁,k₂,..., k_т так, чтобы их сумма была минимальной, т.е. необходимо обратить в минимум форму:

Очевидно, что:

Вероятности р_i можно определить как р_i= k_iV .

Аппарат линейного программирования позволяет путем сравнительно небольшого числа проб подобрать величины k₁,k₂,..., k_т , удовлетворяющие поставленным требованиям.

Для определения оптимальной стратегии противника можно поступить следующим образом: изменить знак выигрыша на обратный, прибавить к каждому элементу платежной матрицы постоянную величину, чтобы сделать их неотрицательными, и решать задачу за второго игрока так же, как она решалась за первого.

p₁d₁ +p₂d₂ +... + p_md_m1 V,

p₁d₂ +p₂d₂ +... + p_md_m2 V,

…

p₁d_1n +p₂d_2n +... + p_md_m V,

Не является исключением в этом и туристический бизнес. Последовательность событий в конфликте персонала туристических фирм зависит от решений, принимаемых каждой из сторон-участников, при этом поведение участника конфликта признаётся разумным и рациональным, если оно принимается с учётом возможного поведения всех остальных участников.

Таким образом, система математических методов, применяемых в принятии управленческих решений в экономике, позволяет соотнести позитивные возможности рыночной инфраструктуры и полезность их применения в сфере туристических услуг.

Литература:

1. Бразовская Н.В., Бразовская О.В. Математические методы принятия управленческих решений: Учебное пособие/Алт. Госуд. Технич. Университет им. И.И. Ползунова.- Барнаул: изд. АлтГТУ, 2004. – 153 с.

2. Ивасенко А.Г. Разработка управленческих решений: учебное пособие – 2-е изд., перераб. И доп. – М.: КНОРУС, 2008 – 168 с.

3. Михненко П.А. Секреты эффективных бизнес - решений. Настольная книга для руководителей. – М.: НТ Пресс, 2007 – 288 с.

4. Парахина В.Н., Максименко Л.С., Панасенко С.В. Стратегический менеджмент: учебник. М: КНОРУС, 2006 – 234 с.

5. http//www.olap.ru//best/analysis.asp

Blog

Математические методы принятия управленческих решений в туризме Мордовченков Н. В

Содержание