Колупаева Галина Геннадьевна с. Чоя 2005 год пояснительная записка

Вид материала

Содержание

Вавилонская нумерация.
Решение задач-ребусов.
Пояснительная записка
Решение геометрических задач – 7 ч
Пояснительная записка
Геометрические задачи.
Занимательные задачи.
Первый год обучения. 5 класс.

Подобный материал:

Внеурочная деятельность по предмету

Содержание:

«Математика вокруг нас» - факультатив 5 класс
«Решение задач повышенной трудности» - факультатив 11 класс
«Решение задач повышенной трудности» - факультатив 8 класс
« Решение нестандартных задач» - факультатив 7 – 8 класс
Секция по математике «Юные математики» 5-6 класс

Муниципальное общеобразовательное учреждение

«Чойская средняя общеобразовательная школа»

(1 час в неделю, всего 34 часа)

Учитель: Колупаева Галина Геннадьевна.

с.Чоя 2005 год

Пояснительная записка.

Одним из направлений в обучении учащихся является расширение кругозора, повышение мотивации учения и самообучения. Кроме этого для успешного усвоения предмета необходимо создать для учащихся ситуацию успеха: дать почувствовать, что они могут найти решение трудных задач. На первом этапе необходимо привить интерес к предмету математика, чему способствует кружок-факультатив «Математика вокруг нас». Тематика факультатива направлена, в первую очередь, на развитие логического мышления, развитие творческих способностей. Кроме этого, на факультативе рассматриваются вопросы, касающиеся исторического возникновения математики, материалы об ученых-математиках, приемы устного счета, запланированы занятия-игры, т.к. дети с большим энтузиазмом и спортивным интересом участвуют в таких играх-состязаниях.

Таким образом, целью данного факультатива является:

развитие логического мышления;
привитие интереса к предмету математика;
развитие творческих способностей;
расширение кругозора.

Задачи данного курса:

вовлечь как можно большее количество учащихся на факультатив;
сформировать навыки решения трудных задач;
организовать занятия-игры, способствующие творческому развитию учащихся.

Формы занятий.

Лекции.
Семинары-практикумы.
Игры-состязания.
Олимпиады.

Система ЗУН.

Знать нумерации (Древнеримская, Египетская, индейцев, Майя, африканцев, древнегреческая, древнеславянская, Вавилонская).
Знать гипотезы происхождения формы арабских цифр.
Знать биографию ученых-математиков (Миниатюры. Пифагор, Архимед, П.Ферма)
Знать приемы устного счета.
Уметь записывать числа в различных нумерациях.
Уметь использовать приемы устного счета.
Уметь решать логические задачи с помощью таблиц.
Уметь решать примеры-ребусы.

Тематический план.

№	Тема урока	Кол-во часов	Литература
1. 2. 3. 4. 5. 6. 7. 8. 9-10 11-12 13-14 15. 16. 17. 18. 19. 20. 21-22. 23. 24. 25. 26. 27. 29. 30-31 32-33 34.	Как люди научились считать. Древнеримская нумерация. Египетская нумерация. Нумерация индейцев майя и африканцев. Древнегреческая и древнеславянская нумерация. Вавилонская нумерация. Гипотеза происхождения формы арабских цифр. «Зеленый калейдоскоп». Старинные занимательные задачи. Пятое математическое действие. Числовые головоломки. Арифметическая викторина. Решение нестандартных задач. Сообразите. Умножение на 5, 25. Умножение на 11. Возведение чисел в квадрат, оканчивающихся 5. Решение олимпиадных задач. Олимпиада. Игра «Крестики-нолики». Математические забавы. Искусство отгадывать числа. Биографические миниатюры. Пифагор., Архимед. Биографические миниатюры П.Ферма. Решение задач-ребусов. Решение логических задач с помощью таблиц. Игра «Веселый калейдоскоп».	1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 1 1 1 1 1 2 2	З.Ш.К. З.Ш.К. МС М.Ш. МС.З.С,З.З. М.С, З.С. З.Ш.К. З.Ш.К. З.Ш.К. М.С М.С М.С М.С З.Ш.К. З.Ш.К. З.Ш.К.

ЛИТЕРАТУРА (сокращения)

ЗШК – Шейнина «Занятия школьного кружка»
Ш.О. – Чулков П.В. «Школьные олимпиады 5-6 кл.».
З.З. – Баврин И.И. «Занимательные задачи по математике».
З.С. – Нестеренко Ю.В. «Задачи на смекалку».
М.С. – Игнатьев «Математическая смекалка».

Муниципальное общеобразовательное учреждение

«Чойская средняя общеобразовательная школа»

Факультатив по математике 11 класс

Учитель: Колупаева Галина Геннадьевна,

учитель математики

с.Чоя 2006 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Факультатив «Решение задач повышенной трудности» предназначен для учеников 11 класса, собирающихся после окончания школы поступать в высшие учебные заведения, в которых предъявляются достаточно высокие требования к математической подготовке абитуриентов и студентов. С его помощью решается конкретно-практическая задача – подготовка выпускников к конкурсному экзамену по математике.

Сейчас главным требованием, предъявляемым к выпускнику, является счетно-аналитические умения и творческие способности. Не секрет, что многие обучающиеся, имеющие «5» за знания в школе, не подтверждают оценку на ЕГЭ или на вступительном экзамене. В связи с этим ведение факультатива сокращает разрыв между имеющимся багажом знаний и требуемым. Многие обучающиеся не владеют различными формами умственной деятельности, решая ту или иную задачу, не всегда ищут различные решения, чаще всего стараются найти стандартный метод, который использует учитель. Но каждая задача имеет идейную и техническую сложность. Идейная часть решения дает ответ на вопрос, как решать задачу. Техническая часть представляет собой реализацию найденной идеи. Есть задачи, в которых главное – найти идею решения, а техническая часть отсутствует или наоборот. Занятия на факультативе должны в равной степени способствовать повышению как идейной, так и технической подготовки обучающихся.

Таким образом, основной целью данного факультатива является:

как можно полнее развить потенциальные творческие способности каждого обучающегося, не ограничивая заранее сверху уровень сложности используемого задачного материала.

Процесс обучения строится на ряде методических принципов:

Принцип регулярности. Основная работа происходит не в классе, а дома, индивидуально. При этом лучше заниматься каждый день по 1 часу, чем 1 раз по многу часов.
Принцип параллельности. Изучать 1 тему, в которую включены задания из ранее изученных.
Принцип опережающей сложности. Задавать на дом 7-8 доступных задач, 3-4 более сложных, 1-2 превышающие возможности самых сильных учеников. Думая над сложной задачей, процесс усвоения новых идей более эффективен.
Принцип самоконтроля. Умение анализировать получившийся ответ с ответом, данным в учебном пособии.

Система ЗУН.

Знать основные этапы и методы решения текстовых задач, уметь решать текстовые задачи на движение, проценты, работу.
Знать и уметь решать уравнения, неравенства и системы уравнений с параметром. Уметь проводить анализ задания, включающего параметр.
Знать методы решения геометрических задач повышенной сложности и решать этими методами.
Знать и уметь решать задачи, содержащие неизвестное под знаком модуля.
Знать и уметь решать различные неравенства.

№ урока	Тема	Дополнительная литература
1-2 3 4-5 6 - 8 9 – 12 13 14 15 16 17 18 19 20 21 22 23 24 25-26 27	Задачи с параметрами – 10ч Решение квадратных уравнений с параметром. Неравенства с параметром. Системы с параметром. Разные задачи. Свойства функций в задачах с параметрами. Текстовые задачи – 4ч. Решение задач на движение. Решение задач с процентами. Решение задач на работу. Арифметическая и геометрическая прогрессии. Задачи, содержащие неизвестное под знаком модуля. Преобразование рациональных выражений 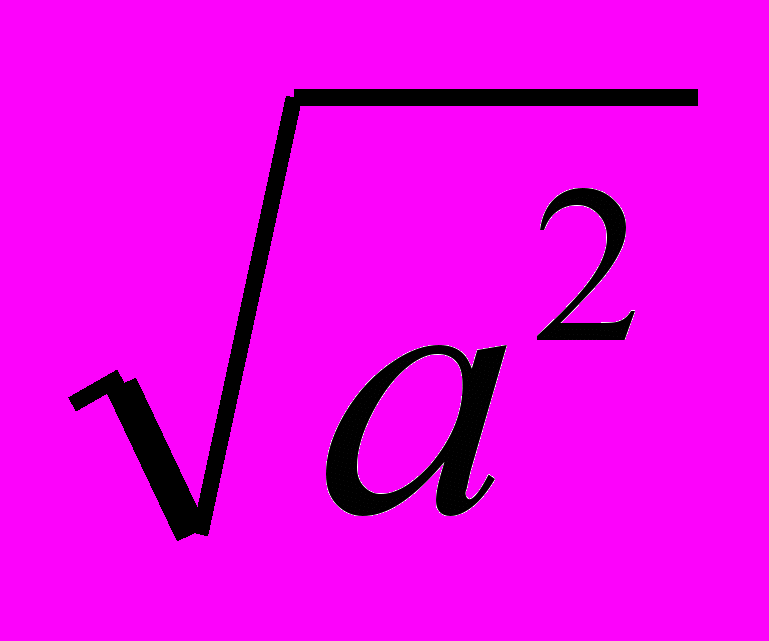= . Построение графика функций у = 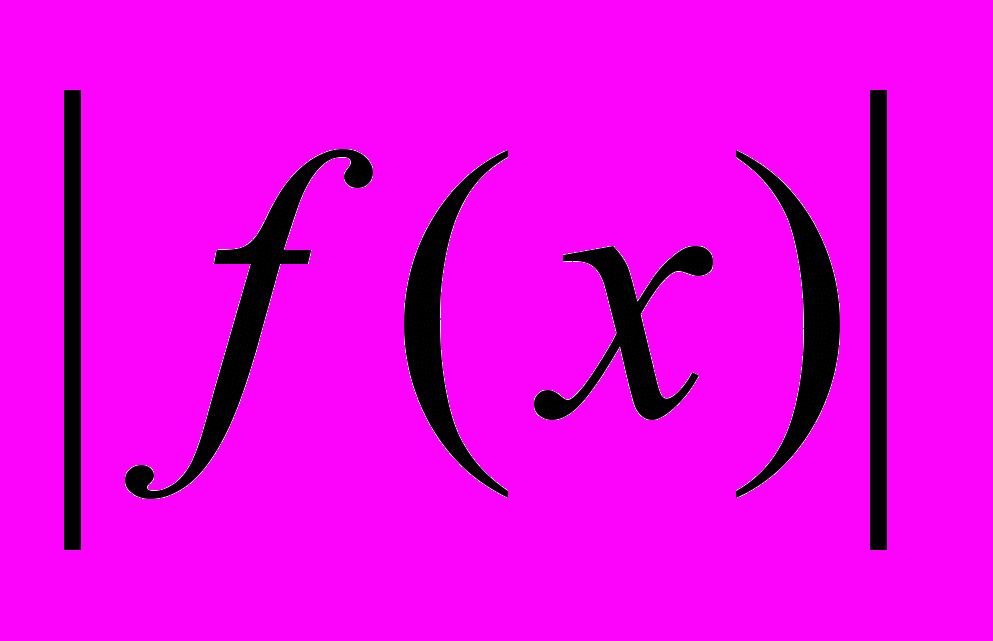и решение уравнений графическим способом. Решение системы, содержащей модуль. Решение уравнений и неравенств, содержащих «модуль в модуле». Решение неравенств с абсолютными величинами. Неравенства. Решение других рациональных неравенств Логарифмические и показательные неравенства. Решение с помощью метода замены переменной. Разные задачи. Задачи на максимум и минимум. Решение геометрических задач – 7 ч Выявление характерных особенностей заданной конфигурации. Геометрические методы решения задач. Аналитические методы. Метод координат. Векторный метод. Разные задачи.	Фальке – стр. 7 Шарыгин стр.105 Шарыгин стр.111 Маркова стр 72 Шарыгин стр. 114, Фальке стр. 10, 21, 28 Шарыгин стр. 120, Фальке стр. 10, 16, 24 Фальке стр.30 -58 Шарыгин Шарыгин Фальке стр. 62 Фальке стр. 72 Фальке стр. 74 Фальке стр. 84 Маркова стр.69 Шарыгин стр. 48 Фальке стр. 88 Фальке стр 92,97 Фальке стр. 95 Фальке стр 102, 107 Шарыгин стр.120. Шарыгин стр. 167 Шарыгин стр. 174 Шарыгин стр. 180 Шарыгин стр. 189 Шарыгин стр. 192 Маркова стр. 68

ЛИТЕРАТУРА

Кохась К.П., Храбров А.И. и др. Задачи Санкт-Петербургской олимпиады школьников по математике 2005 года. – С-Пб.: Невский Диалект: БХВ-Петербург, 2005.

Маркова И.С. – Новые олимпиады по математике. – Ростов-на/Д.: Феникс, 2005.

Фальке Л.Я. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике. – М.: Илекса, Ставрополь: Сервисшкола, 2002.

Шарыгин И.Ф. Факультативный курс по математике: решение задач: Учебное пособие для 10,11 класса средней школы. – М.: Просвещение, 1989.

Газета «Математика». Учебно-методическое приложение к газете «Первое сентября». 2001 – 2004.

Журнал «Математика в школе». Учебно-методическое пособие. 2005.

Муниципальное общеобразовательное учреждение

«Чойская средняя общеобразовательная школа»

Тематическое планирование факультатива

8 класс

(всего 34 часа, 1 час в неделю)

Автор: Колупаева Галина Геннадьевна,

учитель математики.

с.Чоя 2006 год

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Состояние математической подготовки учащихся характеризуется в первую очередь умением решать задачи. С другой стороны, задачи – это основное средство развития математического мышления учащихся. Прежде всего, такими задачами являются нестандартные задачи, поиск которых, по словам академика Гнеденко Б.В., составляют важные слагаемые на пути развития способностей и духа творческого горения.

Целью данного факультатива является:

развитие у учащихся мыслительных способностей, способствующих самостоятельному, творческому мышлению.

Система ЗУН.

Решение задач повышенной трудности требует умения рассуждать, а не решать с помощью готовых формул. Поэтому факультатив способствует познавательной деятельности, активизации мыслительных процессов. Он должен научить учащихся находить пути к решению проблем. Решение нестандартных задач позволяет учащимся накапливать опыт в сопоставлении, наблюдении, выявлять математические закономерности, высказывать догадки, нуждающиеся в доказательстве. Тем самым создаются условия для выработки у учащихся потребности в дедуктивных рассуждениях.

№

Тема

Количество часов

1.

2.

3.

4.

5.

6-7

8-9

10-13

14-17

18-20

21-22

23-24

25-28

29-30

31

32

33

34

Повторение курса 7 класса.

Задачи на движение.

Задачи на делимость чисел.

Задачи с процентами.

Задачи с параметрами.

Нестандартные задачи на формулы сокращенного умножения.

Геометрические задачи.

Отрезки. Прямые.

Параллельные и перпендикулярные прямые.

Треугольники.

Задачи на построение.

Четырехугольники.

Решение задач с параметрами.

Параметр в лин. уравнении.

Параметр в др.-рациональном уравнении.

Параметр в квадратном уравнении.

Параметр в неравенстве.

Занимательные задачи.

Задачи на движение.

Задачи с натуральными числами.

Задачи на нахождение суммы ряда.

Задачи по арифметике.

5

1

1

1

1

1

15

2

2

4

4

3

10

2

2

4

2

4

1

1

1

1

ЛИТЕРАТУРА.

Атанасян. «Геометрия 7-9».
Галицкий. «Сборник задач по алгебре 8-9 кл.».
Звавич Л.И. «Контрольные и проверочные работы по алгебре 7-9».
Игнатьев. «Математическая смекалка».
Каганов. «400 самых интересных задач с решениями».
Кострикина. «Задачи повышенной трудности».
Перельман. «Занимательная алгебра»

Муниципальное общеобразовательное учреждение

«Чойская средняя общеобразовательная школа»

Факультатив по математике

Учитель: Колупаева Галина Геннадьевна,

учитель математики

с.Чоя 2006 год

Пояснительная записка

Первоначальные математические познания должны входить с самых ранних лет в наше образование и воспитание. В связи с этим появилась необходимость в развитии математического мышления у школьников среднего звена. Далеко не секрет, что программа школьного курса не отвечает требованиям современной подготовки выпускников, в основном, обучающиеся могут лишь воспроизвести учебный материал и решить стандартные задания. Но математика тем интересна и полезна, что, используя ее аппарат, можно решать широкий спектр различных практических задач.

Факультатив « «Решение нестандартных задач» направлен в основном на то, чтобы заинтересовать обучающихся, показать им практическое применение своих знаний, научить чувствовать радость от решенной «трудной» задачи. Познав вкус радости от решения проблемы, можно уверенно сказать, что обучающиеся с большей охотой и интересом будут самостоятельно работать, выискивая изюминки в задачах, не бояться трудностей и находить различные пути решения.

Целью данного факультатива является:

Привитие интереса к предмету математика.
Развитие творческих способностей обучающихся, не ограничивая заранее сверху уровень сложности.
Развивать логическое мышление.
Формировать стремление к самосовершенствованию.
Способствовать самообразованию обучающихся.

Методы и приемы обучения.

Семинары-практикумы.
Экскурсии.
Дидактические игры
Тесты.

Система ЗУН.

Знать методы решения логических задач.
Научиться решать логические задачи.
Знать и овладеть приемами устного счета (умножение на 11, 25, 5; возведение в квадрат чисел, оканчивающихся на 5).
Уметь решать комбинативные задачи с числами.
Научиться искать факториал.
Познакомиться с биографией известных математиков: С.В.Ковалевской, Пифагора, И.Ньютона, Лобачевского, Р.Декарта, Гаусса, Эйлера, Галуа.
Научиться готовить сообщения и совершенствовать навыки публичного выступления.
Уметь применять знания на практике.

№ занятия	Тема	Литература
1 2 3 4-6 7-8 9 10 11- 13 14 15 16 17	Вводное занятие. Сказки и старые истории. Решение задач с числами. Экскурсия в лес (измерение обхвата деревьев). Решение логических задач. Приемы устного счета. Умножение на 11, 25, 5, возведение в квадрат чисел, оканчивающихся на 5. Упражнения со спичками. Комбинативные задачи с квадратами. Решение олимпиадных задач. Знакомьтесь, «новый знак». По страницам истории. Игра «Астрономия на координатной плоскости». Викторина «О, математика!».	Игнатьев «Математ.смек.» стр.31. Нестеренко «Зад. на смек.» стр.25, 63. ЗШК стр 174, Нестеренко «Задан. На смек, стр.80,81 Фарков «Гот.к олимп.» стр 33. ЗШК стр. 144 Игнатьев «Матем.смек.» стр 11. Нестеренко «Зад.на смек» стр 28. Игнатьев «Матем.смек.» стр.39. ЗШК, ШО. ЗШК стр.159 ЗШК ЗШК стр. 169 Баврин «Занимат. задачи по математике»

Литература

Баврин И.И., Фрибус Е.А. Занимательные задачи по математике – М.: Гуманитарный издательский центр ВЛАДОС, 2003.

Игнатьев Е.И. Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы. – М.: Омега, 1994.

Нестеренко Ю.В. Задачи на смекалку. – М.: Дрофа, 2003.

Фарков А.В. Готовимся к олимпиадам по математике: учебно-методическое пособие. – М.: Издательство «Экзамен», 2006 г.

Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 кл. – М.: Издательство НЦ 7НАС, 2002.

Тематическое планирование секции по математике

«Юные математики»

5-6 класс.

Учитель: Колупаева Г.Г.

Количество часов – 33.

Цель занятий:

развивать интерес к математике;
ознакомить учащихся с историей развития математики;
формировать творческое мышление.

Система ЗУН:

творчески подходить к поиску решения занимательных задач;
вырабатывать навык самостоятельной деятельности;
уметь владеть способами решения стандартных и нестандартных задач.

Пояснительная записка

Для развития познавательной активности и самостоятельности учащихся, необходимо закладывать творческий поиск, увлеченность, целеустремленность и чувство ответственности перед самим собой. Необходимо развивать творческое мышление у учащихся, позволяющее решать сложные и нестандартные задачи, применять или находить оригинальные и нешаблонные пути решения.

Именно систематическая работа над усовершенствованием творческой деятельности может осуществляться на секционных занятиях. Невозможно повысить интерес к предмету только учебным материалом без дополнительной занимательной и развивающей информации.

Первый год обучения. 5 класс.

№	Содержание материала	Кол-во часов	Литература
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27.	Как возникла наука «математика» а) как возникло слово «математика» б) задачи Древнего Египта в) занимательная математика. а) Счет у первобытных людей. б) Логические задачи. в) Математическая игра «Не собьюсь». Математические тесты. Приемы устного счета. а) признаки делимости б) задачи Древнего Вавилона в) задачи на смекалку. а) цифры у разных народов б) умножение двухзначных чисел на 11 в) решение логических задач. Решение олимпиадных задач. В мире больших чисел а) математика в Древней Греции б) интересные способы умножения в) решение олимпиадных задач. Решение логических задач. а) Биографические миниатюры об ученых: Пифагор, Евклид, Архимед. б) решение нестандартных задач. Решение нестандартных задач. Приемы устного счета а) задачи Древнего Китая б) возведение в квадрат чисел, оканчивающихся на 5. в) задачи головоломки. Математические тесты а) Метрическая система мер б) решение олимпиадных задач Геометрия Гулливера а) геометрия как наука б) геометрические головоломки. Метод проб и ошибок. Методы решения задач. Лабиринт. Решение логических задач матричным способом. Математические игры. Как ценили математику наши предки а) математика у русского народа б) старинные меры в) решение олимпиадных задач. Решение логических задач. Внутриклассная олимпиада. а) Математики шутят. б) задачи – шутки. а) Тренировка памяти и внимания. б) логическая задача «Обманутый хозяин». а) приемы устного счета б) решение олимпиадных задач. а) Происхождение математических знаков б) математические забавы Лермонтова Магницкого Задача-сказка. Составление задач. Решение математических кроссвордов. Итоговое занятие.	1 1 1 1 1 2 2 IIчетверть 1 1 2 1 1 1 III четверть 1 1 2 1 1 2 1 IV четверть 1 1 1 1 1 2 1	1) О.С.Шейнина «Занятия школьного кружка» 2) И.Депман «Рассказы о математике». 3) И.И.Баврин «Занимательные задачи по математике». 4) Ю.В. Нестеренко «Задачи на смекалку». 1. О.С.Шейнина стр.13-15. 5) Н.ВСавинцева «Я иду на урок математики» 1) стр.10 3) стр. 10 4) стр. 7-8 стр. 17-21 6) Задания московской олимпиады. №3 стр.12-13 № 1 стр. 22-24 Газета «Математика» № 3 стр.15-19 № 1 стр.29-30 Стр. 58 № 1 стр. 32-33 Виленкин «Математика 5» № 3 стр. 24-25 № 1 стр. 20 № 4 стр. 10 № 5 стр.22-25 № 1 стр.37-40 № 2 стр. 117 № 1 стр.41-42 № 1 стр. 44-46 № 1 стр. 46-48 № 1 стр. 15, 35, 49 № 2 стр. 31 № 1 стр. 62 № 1 стр.43 № 4 стр. 16-17 Московские олимпиады № 3 стр.83, № 4 , № 1 стр.52,56 № 1 стр.68 № 1 стр.71 № 1 стр.54 № 1 стр.55, стр. 70 № 1 стр.73 № 2 стр. 63-69 № 1 стр. 76-78

Литература

О.С.Шейнина, Г.М.Соловьева. «Занятия школьного кружка». Москва 2002 г.
И.Депман «Рассказы о математике». Ленинград 1954 г.
И.И.Баврин, Е.А.Фрибус «Занимательные задачи по математике» , Москва 1999 г.
Ю.В.Нестеренко «Задачи на смекалку», Москва 2003 г.
Н.В.Савинцева. «Я иду на урок математики». Тесты Москва 2000 г.
Московские олимпиады по математике.
Газета «Математика» 2000-2003 г.

Тематическое планирование факультатива по математике 6 класс

(второй год обучения)

№	Содержание материала	Кол-во часов	Литература
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.	Интересные свойства чисел: а) биографические миниатюры Л.-Ф.Магницкий б) решение олимпиадных задач в) задача-сказка «Бездельник и черт» Приемы устного счета: а) умножение на 155 и 175 б) биографическая миниатюра Блез паскаль. в) решение олимпиадных задач. Умножение двузначных чисел, близких к 100: а) Рене Декарт – биографическая миниатюра. б) решение олимпиадных задач. в) о «происхождении» дробей. Деление на 5 (50), 25 (250): а) решение олимпиадных задач б) развивающая игра «Попробуй сосчитай». Способы сложения многозначных чисел а) Карл Фридрих Гаусс б) юмористическая страничка в) решение олимпиадных задач Умножение на 9, 99, 999 а) задачи, приписываемые Л.Эйлеру. б) биографическая миниатюра Л.Эйлер в) как играть, чтобы не проиграть. Некоторые особые случаи счета: а) феномены б) решение олимпиадных задач. Из истории интересных чисел. Число П а) приемы умножения на 111. б) биография Н.И.Лобачевского. в) поэзия уравнений г) решение олимпиадных задач. Число Шехерезады а) приемы устного счета б) биография П.Л.Чебышева в) простые числа г) решение олимпиадных задач. Мгновенное умножение а) возраст и математика б) задачи со спичками в) математические софизмы г) задачи в стихах. Признак делимости на 11 а) биография М.В.Остроградского б) игра «Кубики» в) решение олимпиадных задач. Распространение десятичных дробей а) умножение крестиком б) биография Э.Галуа. в) знакомство с новым знаком «!» факториал. г) решение олимпиадных задач. Биография С.В.Ковалевской а) устный счет в сказках. б) геометрическая задача в) решение олимпиадных задач. Принцип Дирихле и его примечание к решению задач а) решение олимпиадных задач б) биография Норберта Винера в) игра «Астрономия на плоскости» Проведение внутриклассной олимпиады. Решение олимпиадных заданий. Разбор результатов внутриклассной олимпиады. Составление математических задач и кроссвордов.	1 1 1 1 II четверть 1 1 1 1 III четверть 1 1 1 1 1 IV четверть 1 1 1 2	№ 1 стр. 103-108 Стр. 79-84 Стр. 85-90 № 1 стр. 97-102 Стр.109-113 № 1 стр.115 – 120 № 1 стр.122-127 № 1 стр. 123-133 № 1 стр. 135-142 № 1 стр. 143-148 № 1 стр.150-154 № 1 стр. 155-159 № 1 стр. 161-165 № 1 стр. 166-173 № 3, № 4, № 6.

Колупаева Галина Геннадьевна МОУ «Чойская СОШ» Страница

Blog

Колупаева Галина Геннадьевна с. Чоя 2005 год пояснительная записка

Содержание