Решение математических задач как средство
| Вид материала | Решение |
СодержаниеБиблиографический список |
- Решение, 562.63kb.
- Сетевой уровень как средство построения больших сетей, 1776.72kb.
- Кандидатской диссертации: "Решение задач комбинаторного характера как средство развития, 18.33kb.
- Методы математических рассуждений и доказательств. Примерное содержание, 10.25kb.
- Решение задач при изучении математики играет весьма существенную роль, т к. с помощью, 258.56kb.
- Решение математических и экономических задач средствами matlab, 11.27kb.
- Тема: Построение математических моделей как предварительный этап алгоритмизации. Цель, 110.57kb.
- Программа по английскому языку, 397.9kb.
- Чеботарева Фаина Мэлсовна учитель математики высшей категории средней общеобразовательной, 155.8kb.
- Методика использования компьютерных моделей в обучении школьников 10-11 классов решению, 40.67kb.
Заключение Анализируя проделанную работу можно сделать ряд выводов: 1. Изучив и проанализировав психологическую и методическую литературу, мы исследовали подходы к определению понятия критического мышления, уточнили это понятие применительно к предмету математика. 2. Проанализировали педагогические подходы к изучению методов обучения математике. Систематизировали методические приемы по решению задач, способствующих развитию критического мышления. Дали характеристику методики работы над поиском решения задач. 3. Анализ учебного материала, предшествующий практической части работы, позволил структурировать отобранный учебный материал наиболее логичным и приемлемым способом, в соответствии с целями исследования. 4. Экспериментальные занятия по курсу математики в 7 классах МОУ «Гимназия» были достаточно продуктивны. Нам удалось достичь основной цели данного исследования — выработать ряд методических приемов решения математических задач, направленных на развитие критического мышления. Результатом проведенной работы являются несколько методических рекомендаций к курсу математики: 1) В целях совершенствования преподавания математики целесообразна дальнейшая разработка новых методик использования нестандартных задач. 2) Систематически использовать на уроках задачи, которые направлены на развитие критического, логического, творческого мышления учащихся, на формирование познавательного интереса и самостоятельности. 3) Осуществляя целенаправленное обучение решению задач, учить детей поиску ошибок в рассуждениях, нацеливать на выбор рационального способа решения, анализировать и критически оценивать полученный результат. 4) Целесообразно использование на уроках задач на сообразительность, задач-шуток, математических ребусов, софизмов. 5) Учитывать индивидуальные особенности школьника, дифференциацию познавательных процессов у каждого из них, используя задания различного типа. В результате проведенного педагогического эксперимента можно сделать вывод о том, что развитию критического мышления у обучающихся способствует систематическое использование на уроках предложенных рекомендаций. Таким образом, цель исследования достигнута, гипотеза доказана. Библиографический список
Приложение 1 Самостоятельная работа №1. 1. Решите уравнение 3(6х-2)=-6+6(3х-1,5) и выберите ответ. а) -9; б) -⅔; в) любое число; г) нет решения; д) верного ответа нет. 2. Корнями какого уравнения являются числа: -0,5; 0; 3,8; 101? а) 6х-0,8=3х+22; б) 2х-(6х-5)=45; в) 7х-(х+3)=3(2х-1); г) 5х+3=7х-5(2х+1); д) ни одного. 3. Решите уравнение и определите, какому неравенству удовлетворяет корень уравнения  . .а) х≥-7; б) -7< х≤0; в) -7< х≤7; г) х≤7; д) верного ответа нет. 4. Оцените, можно ли на полку, выдерживающую 50 кг, положить 180 пачек чая по 150 г каждой? Сколько нужно коробок, чтобы разложить весь чай, если в одну коробку входит 400г чая? 5. Лодка, собственная скорость которой равна 7 км/ч догнала плот, находившийся от нее на некотором расстоянии вниз по течению реки, за 30 мин. Какое расстояние было между лодкой и плотом в начале движения, если скорость течения реки равна 3,2 км/ч? 6. Длина прямоугольника на 3,6 см больше ширины, а ширина составляет  его периметра. Какова площадь прямоугольника? его периметра. Какова площадь прямоугольника?Приложение 2 Самостоятельная работа №2. 1. Сколько решений имеет система уравнений 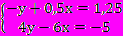 ? ?а) единственное решение; б) не имеет решений; в) бесконечно много решений. 2. Установите соответствие между предложенными парами чисел и системами: 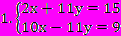 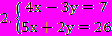 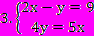 а) (12;15); б) (4; 3); в) (-2; 6); г) (2; 1). 3. В какой координатной четверти лежит точка пересечения прямых 5(х-у)=10 и 3х-7у=20-(х+3у) ? а) в первой; б) во второй; в) в третьей; г) в четвертой; д) нужного ответа нет. 4. Из 48 красных гвоздик, 72 белых гвоздик и 120 розовых гвоздик составили одинаковые букеты. Их число было более 20. Сколько букетов составили? 5. Моторная лодка за 2 часа против течения реки прошла расстояние, на 25% меньшее, чем за то же время по течению. Какова собственная скорость лодки, если скорость течения равна 2,5 км/ч. Есть ли лишнее данное в условии задачи? 6. В магазин поступили учебники по физике и математике. Когда продали 50% учебников по математике и 20% учебников по физике, что составило в общей сложности 390 книг, учебников по математике осталось в 3 раза больше, чем по физике. Сколько учебников по математике и сколько по физике поступило в магазин? |
