Элективный курс по предпрофильной подготовке учащихся 9 классов посвящен одной из важных тем «Уравнения»

Вид материала

Элективный курс

Содержание Учебно-тематический план Количество часов 9. Контрольная работа Самостоятельная работа №10 11-15,5 баллов

Подобный материал:

• Рабочая программа элективного курса по математике «Знакомьтесь: модуль и параметры!», 100.3kb.
• Элективный курс по географии для 9 класса «Демографические проблемы России», 69.94kb.
• Элективный курс «Уравнения и неравенства с модулем» 10 класс разработан учителем моу, 93.7kb.
• Курс предпрофильной подготовки учащихся с ориентацией на информационно-технологический, 59.17kb.
• Элективный курс по географии для 8-9 класса «Многонациональный Костромской край», 61.14kb.
• Чулкова Марина Николаевна, учитель математики элективный курс, 67.8kb.
• Волжска Республики Марий Эл Разработала и провела учитель математики Попова Л. З. Уравнения, 33.26kb.
• Пояснительная записка. Аннотация. Элективный курс «История в ячейках таблицы Менделеева»., 105.34kb.
• Кайгородова Людмила Николаевна, учитель математики, высшая квалификационная категория, 203.47kb.
• Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный, 242.74kb.

Пояснительная записка


Элективный курс по предпрофильной подготовке учащихся 9 классов посвящен одной из важных тем «Уравнения». При решении многих заданий используется эта тема. В последнее время в материалах выпускных экзаменов в форме ГИА и ЕГЭ и вступительных экзаменах в техникумы и ВУЗЫ, предлагаются задания по этой теме.

Курс предназначен для дополнения и углубления знаний по математике. При изучении курса угроза перегрузок учащихся отсутствует, соотношение между объемом предлагаемого материала и временем, необходимым для его усвоения оптимально. Курс соответствует возрастным особенностям школьников и предусматривает возможности индивидуализации и дифференциации процесса обучения. Данная программа предполагает использование активных методов и форм обучения, содержит развивающий потенциал. Курс был предложен родителям на родительском собрании и нашел их одобрение.

Изучение основных положений теории многочленов позволяет обобщить т. Виета для уравнений любой степени. Умение выполнять деление многочлена на многочлен обеспечит в дальнейшем решение таких задач математического анализа, как нахождения асимптот, вычисления производных, интегралов. Умение решать уравнения с модулем, параметром позволяет расширить круг показательных, тригонометрических, логарифмических, иррациональных уравнений и неравенств.

Задачи по теме вызывают затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках мало.

Занятия включают в себя теоретическую и практическую части: лекции, беседы, консультации, практикумы, презентацию, самостоятельные, тестовые, исследовательские работы.

Эффективность обучения отслеживается следующими формами контроля: самостоятельная работа, тест, итоговый контроль. Итоговый контроль предусматривает выполнение зачета.

Курс рассчитан на 17 часов. Занятия проводятся один раз в неделю.

Тема элективного курса актуальна и может быть использована учителями математики других общеобразовательных школ.


Цель:


Изучение некоторых классов уравнений, методов их решения, подкрепленное необходимым теоретическим материалом. Формировать у учащихся умения и навыки по решению уравнений.


Задачи:

1. Познакомить учащихся с теорией многочленов.

2. Обобщить и систематизировать знания учащихся о квадратичной функции в предлагаемых задачах с параметрами

3. Сформировать представление о методах и способах решения нестандартных задач и уравнений на уровне, превышающий уровень обязательного минимума содержания образования.

4.Сформировать способность к осознанному выбору дальнейшего профиля обучения в старшей школе.


Содержание


Тема 1 Многочлен (1 час)

Определение многочлена, сложение, вычитание, умножение и деление многочлена на одночлен и многочлена на многочлен.

Форма контроля: самостоятельная работа.


Тема 2 Теорема Безу. Схема Горнера.(1 час)

Теорема Безу, рациональные корни уравнения. Схема Горнера.

Форма контроля: самостоятельная работа.


Тема 3 Квадратные уравнения.(2 часа)

Знаки корней квадратного уравнения. Расположение корней квадратного уравнения в зависимости от параметра.

Определение квадратного уравнения с параметрами. Способы решения уравнения. Определение знаков корней квадратного уравнения от значения параметра. Теорема о расположении корней квадратного трехчлена относительно заданной точки или заданного числового промежутка. Наибольшее и наименьшее значение квадратичной функции.

Форма работы: исследование.

Форма контроля: самостоятельная работа.


Тема 4 Теорема Виета и обобщенная теорема Виета((1час).

Теорема Виета, примеры применения теоремы и обратной. Применение теоремы для уравнения высших степеней.

Форма контроля: самостоятельная работа.


Тема 5 Целые уравнения(1 час)..

Целые уравнения. Теорема о числе корней многочлена и разложение его на линейные множители. Связь между корнями многочлена и его коэффициентами.

Форма контроля: тест, самостоятельная балловая работа.


Тема 6 Возвратные уравнения(2 часа)

Возвратные уравнения, способы их решения.

Форма контроля: самостоятельная работа.


Тема 7 Симметрические уравнения(1 час).

Определение симметрических уравнений, способы их решения.

Форма контроля: самостоятельная работа.


Тема 8 Уравнения с модулем(2 часа).

Модуль числа. Геометрическое определение модуля. Уравнения, содержащие один и несколько модулей.

Форма контроля: тест


Тема 9 Уравнения с параметрами(3 часа).

Линейные, дробно- линейные, квадратные уравнения с параметрами. Решение уравнений, содержащих параметры.

Форма контроля: контрольная работа.


Тема 10 Рациональные уравнения(2 часа).

Разложение на множители. Формулы сокращенного умножения. Алгоритм решения дробно-рациональных уравнений.

Форма контроля: тест, самостоятельная балловая работа.


Учебно-тематический план

Тема	Формы работы		Формы контроля	Количество часов
	Теоретическая часть	Практическая часть
1. Понятие многочлена. Действия с многочленами. Деление многочлена с остатком.	Беседа	Практикум	Самостоятельная работа	1 час
2. Теорема Безу. Схема Горнера.	Лекция	Практикум	Самостоятельная работа	1 час
3. Квадратные уравнения. Знаки корней квадратного уравнения. Расположение корней квадратного уравнения в зависимости от параметра.	Консультации	Исследовательская работа	Самостоятельная работа	2 часа
4. Теорема Виета и обобщенная теорема Виета.	Лекция	Практикум	Самостоятельная работа	1 час
5. Целые уравнения	Самостоятельная работа с математическим словарем, математической литературой	Практикум	Тест, самостоятельная балловая работа	1 час
6. Возвратные уравнения	Лекция	Практикум	Самостоятельная работа	2 часа
7.Симметрические уравнения	Лекция-беседа	Практикум	Самостоятельная работа	1 час
Уравнения с модулем	Лекция, беседа	Практикум, презентация	Тест .	2 часа
Уравнения с параметром.	Лекция	Исследование , практикум	Контрольная работа.	3 часа
Рациональные уравнения	Беседа, доклады учеников	Практикум	Тест, самостоятельная балловая работа	2 часа
Итоговый контроль курса			Зачет	1 час
Итого				17 часов

Ожидаемые результаты


По окончании изучения курса учащиеся должны уметь:

1. Выполнять действия над многочленами.
   
2. Использовать обобщенную теорему Виета для решения задач повышенного уровня.
   
3. Решать уравнения с модулем и параметрами.
   
4. Применять алгоритмы решения симметрических и возвратных уравнений.
   

По окончании изучения курса учащиеся должны знать:


1. Основные определения и понятия по программе курса.

2. Обобщенную теорему Виета для уравнений высших степеней.

3. Формулировку теоремы Безу.

4. Общие методы решения уравнений: метод замены переменной, разложение на множители, графический метод, группировка.

5. Общий вид уравнений.

6. Определение модуля. Геометрическое определение модуля. Подходы к решению уравнений, содержащих один и более модулей.

7. Методы решения возвратных, симметрических, рациональных, целых уравнений.

Литература


1.Антипов С.А. Предпрофильная подготовка учащихся 9 классов.- М.,2006.

2.Богатырев Г.И. Повторим математику.- М.: Высшая школа, 1968.

3.Дорофеев Г.В. Алгебра, функции, анализ данных 9 класс.- М.,Просвещение,2001.

4.Никольская И.Л. Факультативный курс по математике 7-9 классов.- М.: Просвещение, 1991.

5.Солуковцева Л. Линейные и дробно-линейные уравнения и неравенства с параметрами библиотека // Первое сентября.-2007.-№1(13) .

6.Червякова Н.Г. Материалы тренинга по подготовке ЕГЭ по математике Уравнения и неравенства, содержащих модуль.- Владимир, 2007.

7.Шарыгин И.Ф. Факультативный курс по математике 10 класс.- М: Просвещение, 1989.


Приложение


Самостоятельная работа №1


1. Разделите с остатком следующие многочлены: (х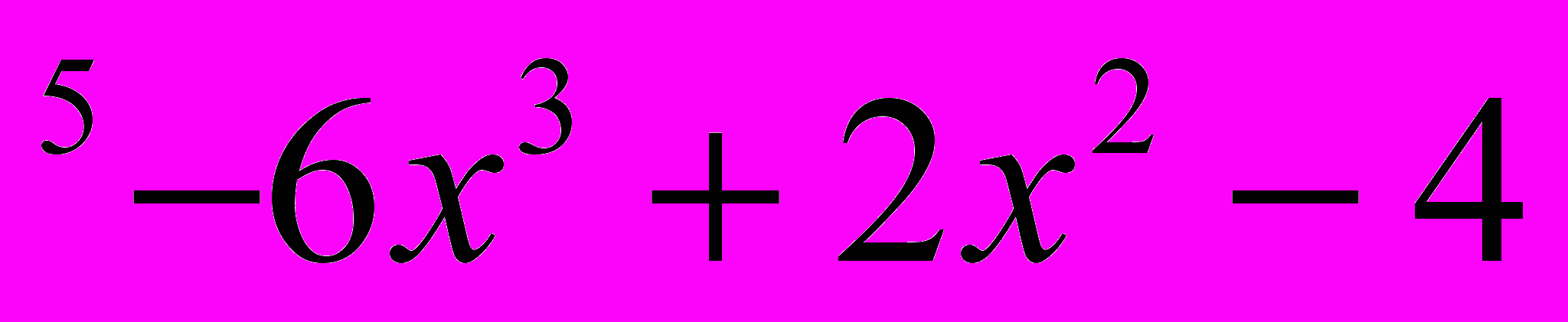) : ( х)


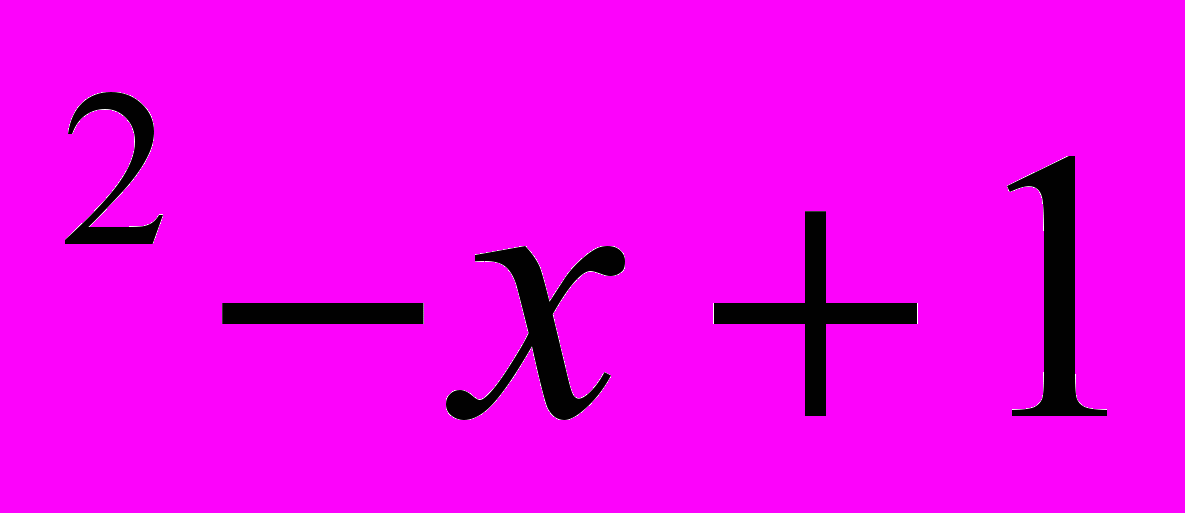( х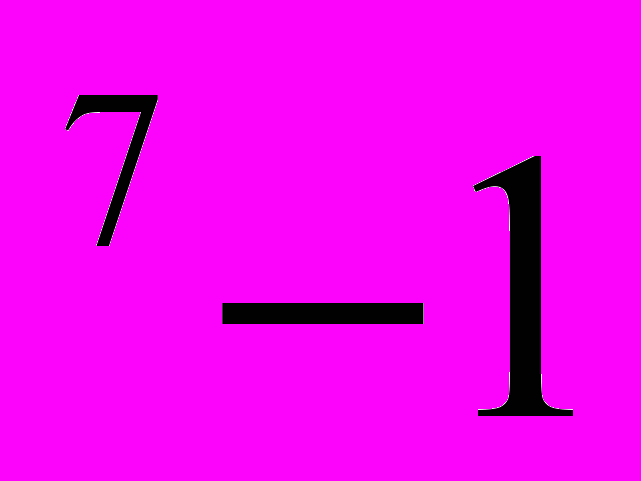): ( х).

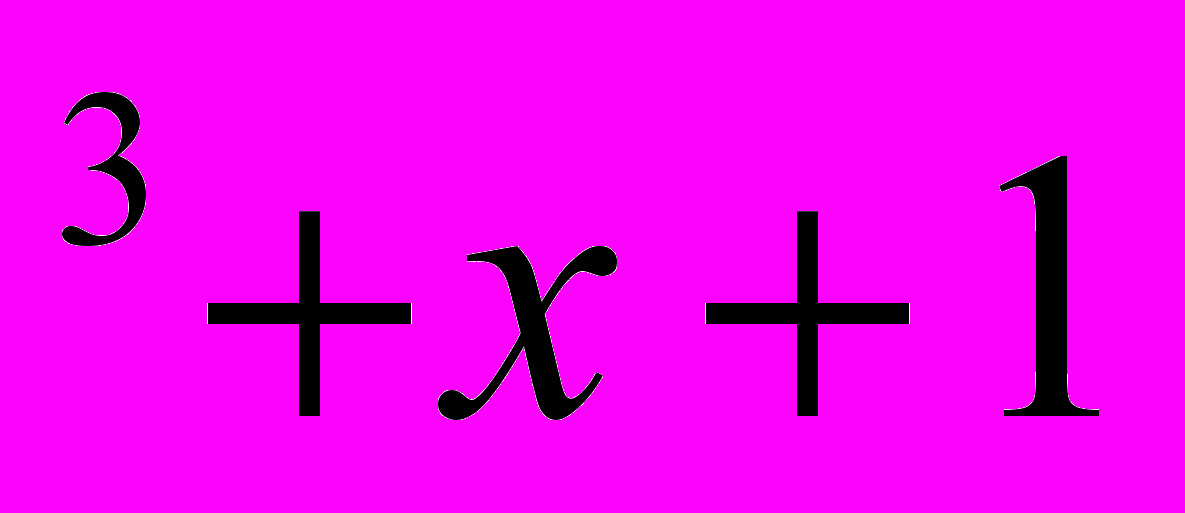2. При каком значении k выполняется без остатка деление: (х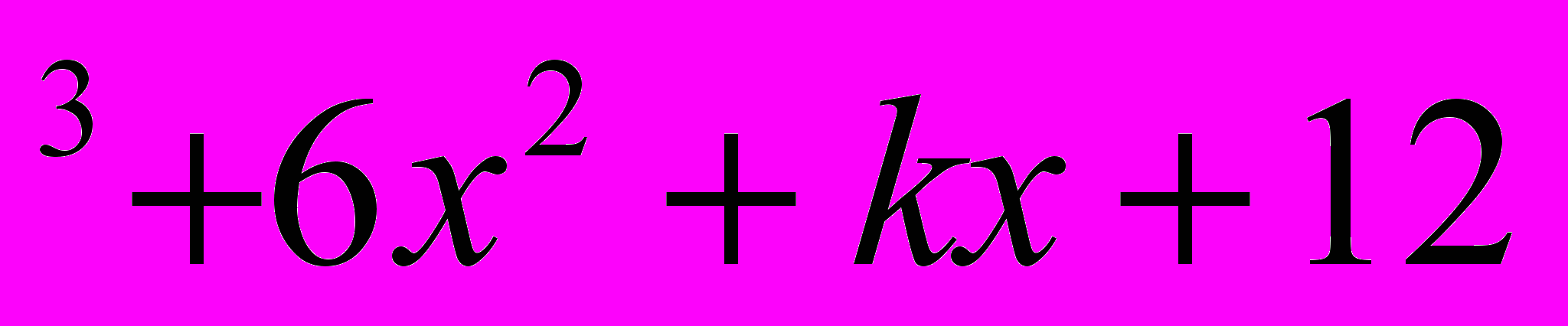): (х+4).


Самостоятельная работа №2


1. Доказать, что – 39 является остатком от деления многочлена А(х)=х

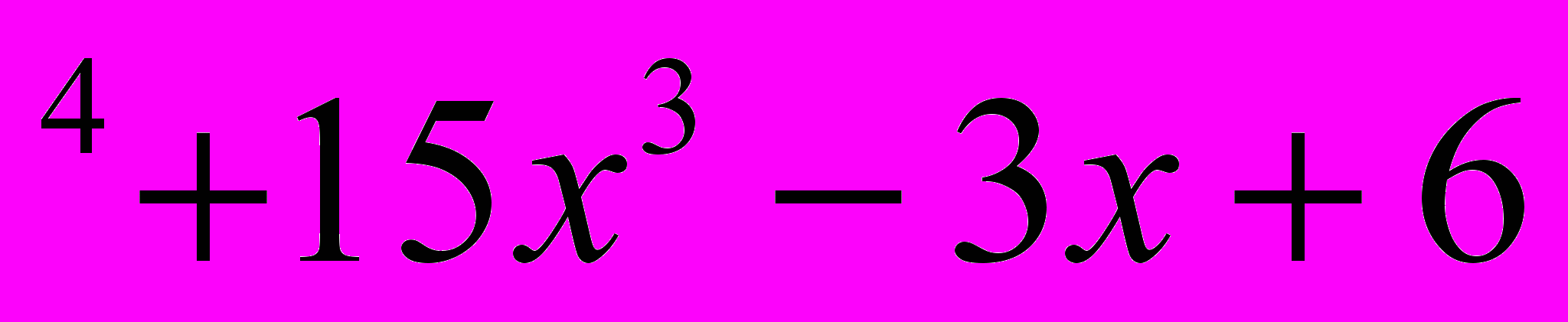
на х+3.

2. Доказать, что 2 является корнем кратности 2 для многочлена А(х)= х.
   

Исследовательская работа


Пусть f(х)=ах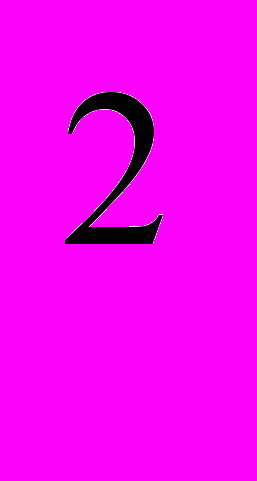+вх+с квадратичная функция, х 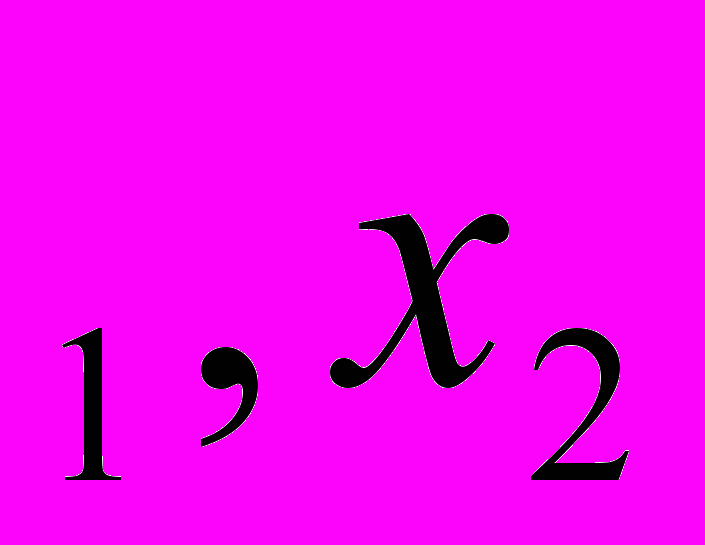корни трехчлена, N некоторое действительное число. Исследуйте расположение корней относительно заданной точки. Какие условия должны при этом выполняться?


Самостоятельная работа№3

1. При каком значении а уравнение (а+5)х 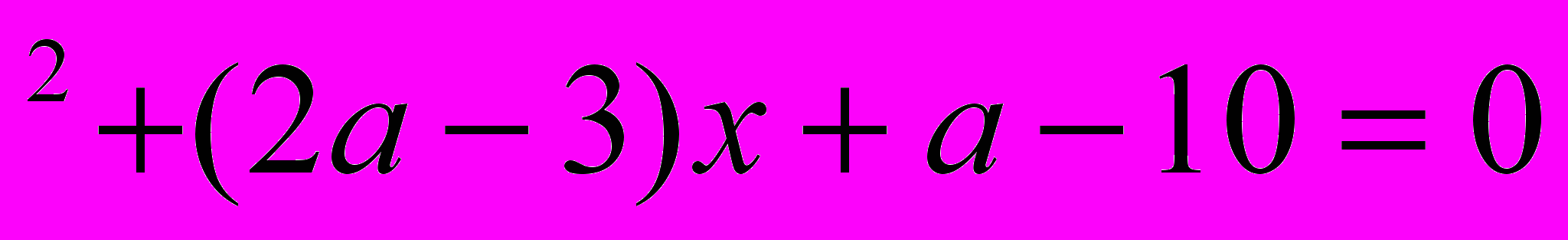имеет два различных отрицательных корня?
   
2. При каких значениях параметра а уравнение 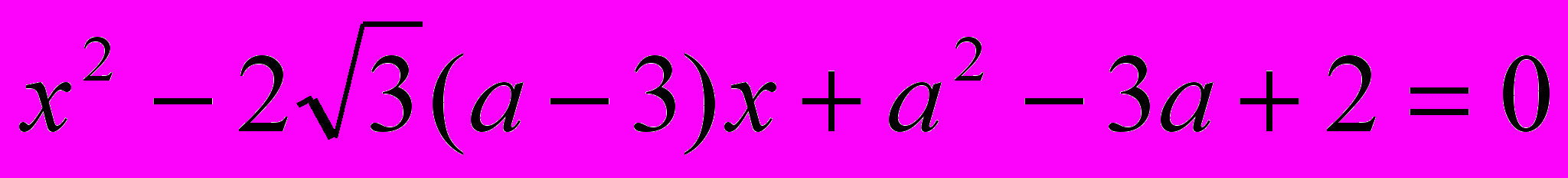имеет два действительных различных корня?
   
3. При каких значениях параметра а корни уравнения а 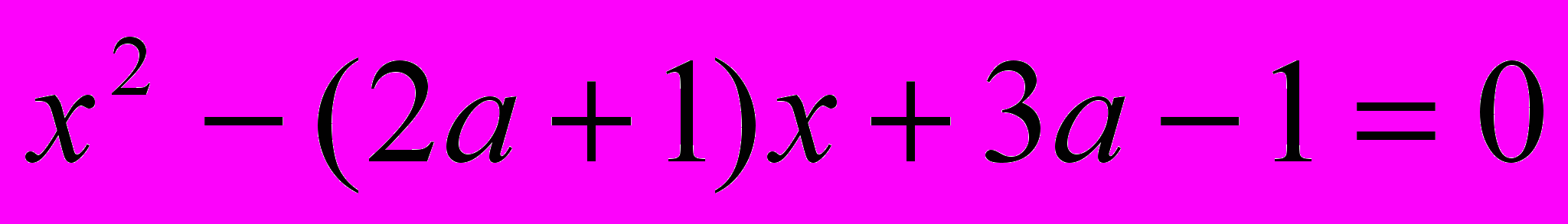больше 1?
   
4. Найти наибольшее и наименьшее значение функции у = 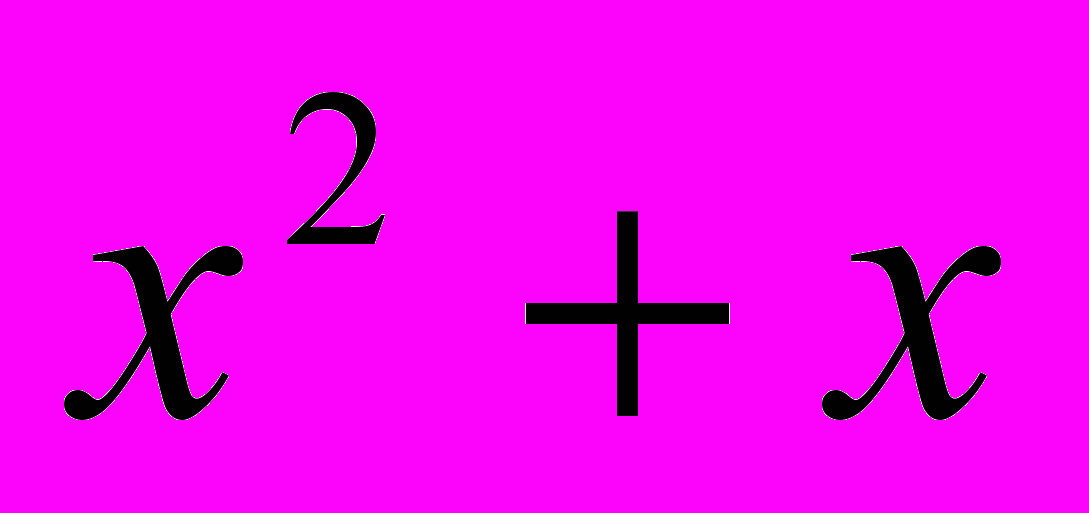на отрезке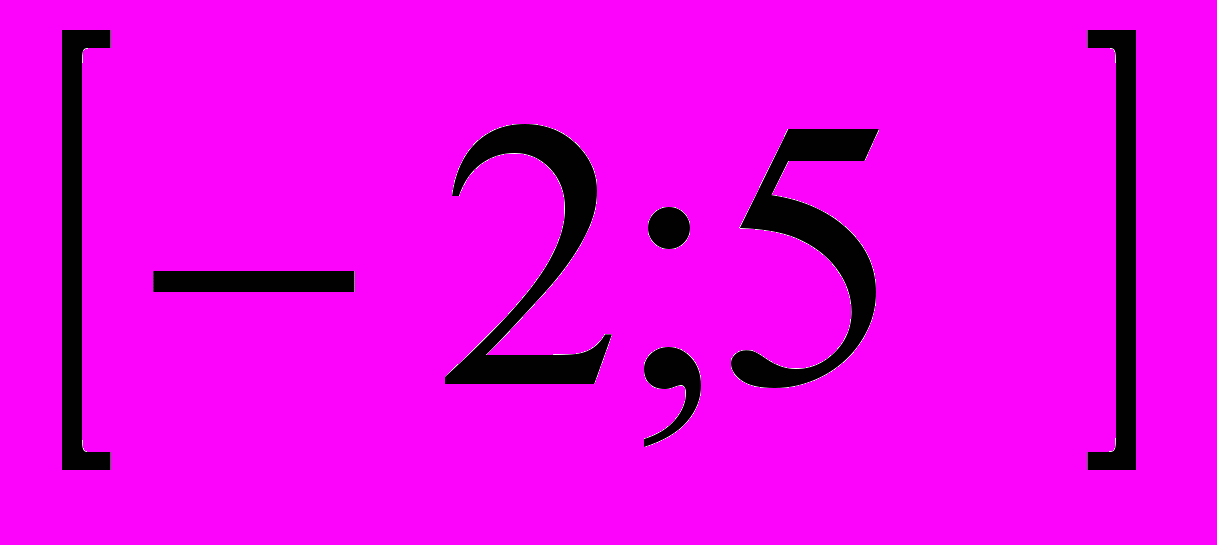
   

Самостоятельная работа №4

1. Напишите квадратный трехчлен, корни которого равны квадратам корней трехчлена .
   
2. В уравнении 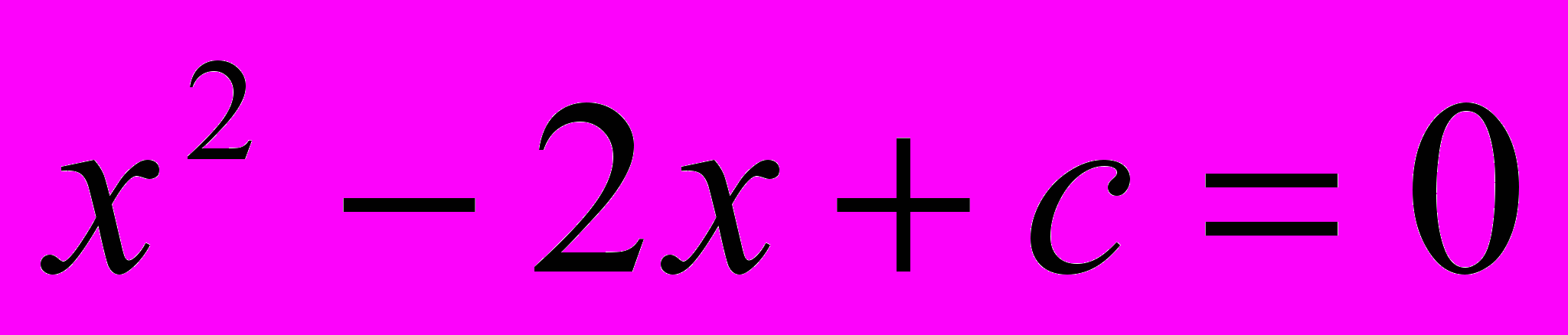определите то значение с, при котором его корни удовлетворяют условию 7.
   
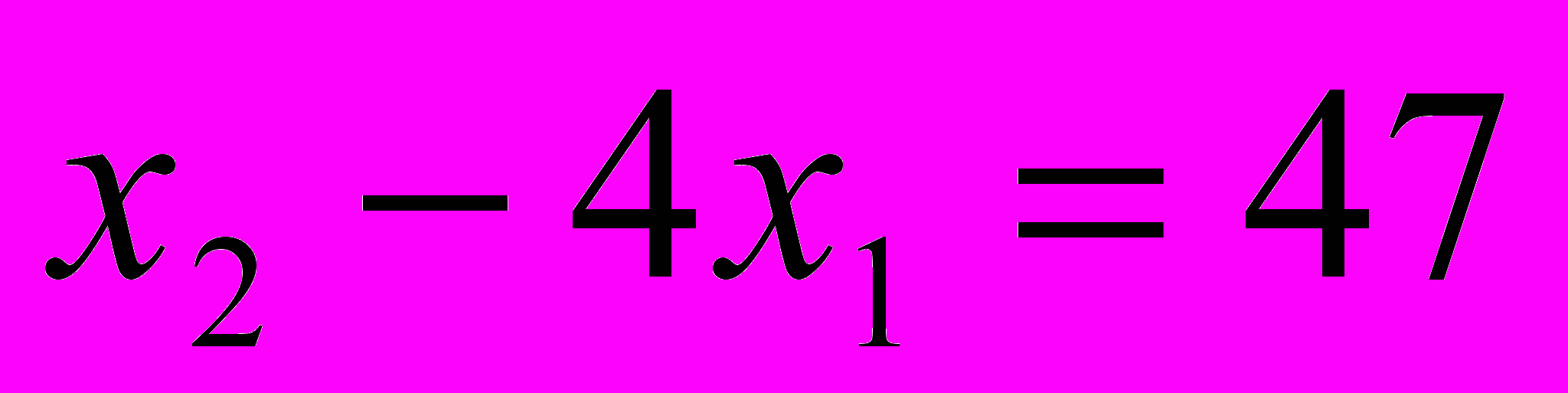3. Составьте кубический многочлен, имеющий корень 5 кратности1 и корень -4 кратности 2.
   
4. Тест, самостоятельная балловая работа.
   

Оценка	«3»	«4»	«5»
Количество баллов	4-8 баллов	9-16 баллов	17-22 балла

Задания первой части оценивается в 0,5 балла.








Самостоятельная работа №6

1. Решите уравнение .
   
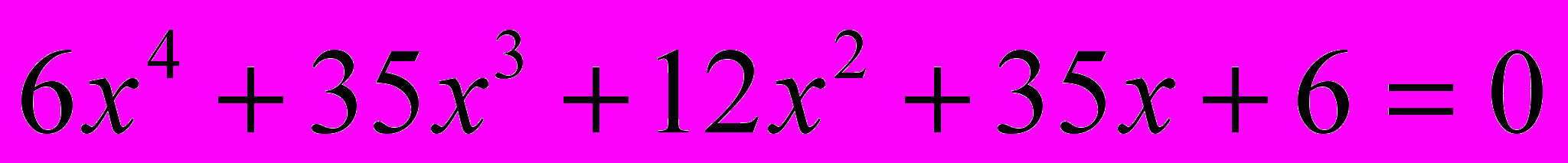2. Найдите сумму наибольшего и наименьшего корней уравнения
   

.


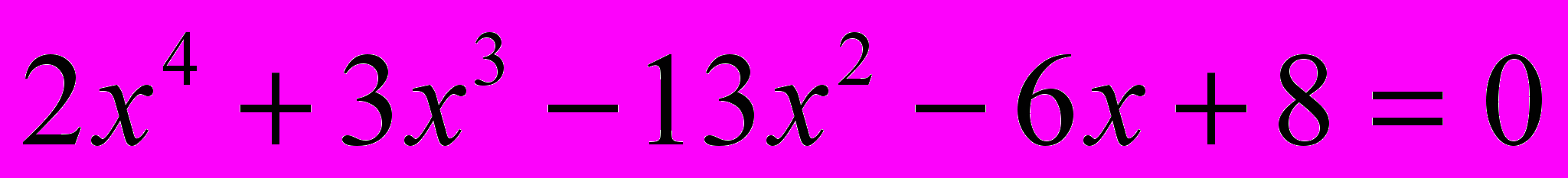Самостоятельная работа №7

1. Решите уравнение .
   
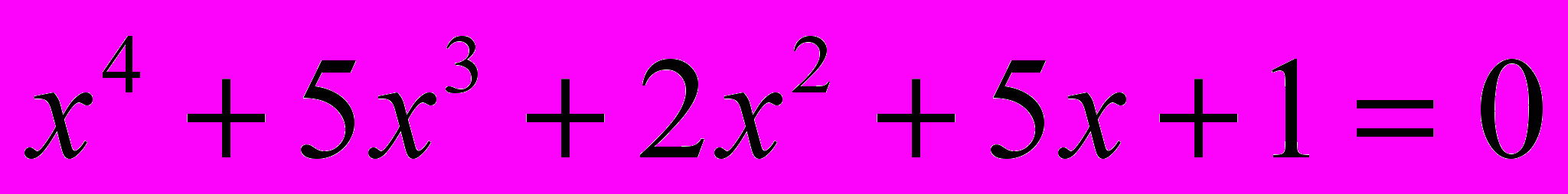2. Сколько корней имеет уравнение .
   

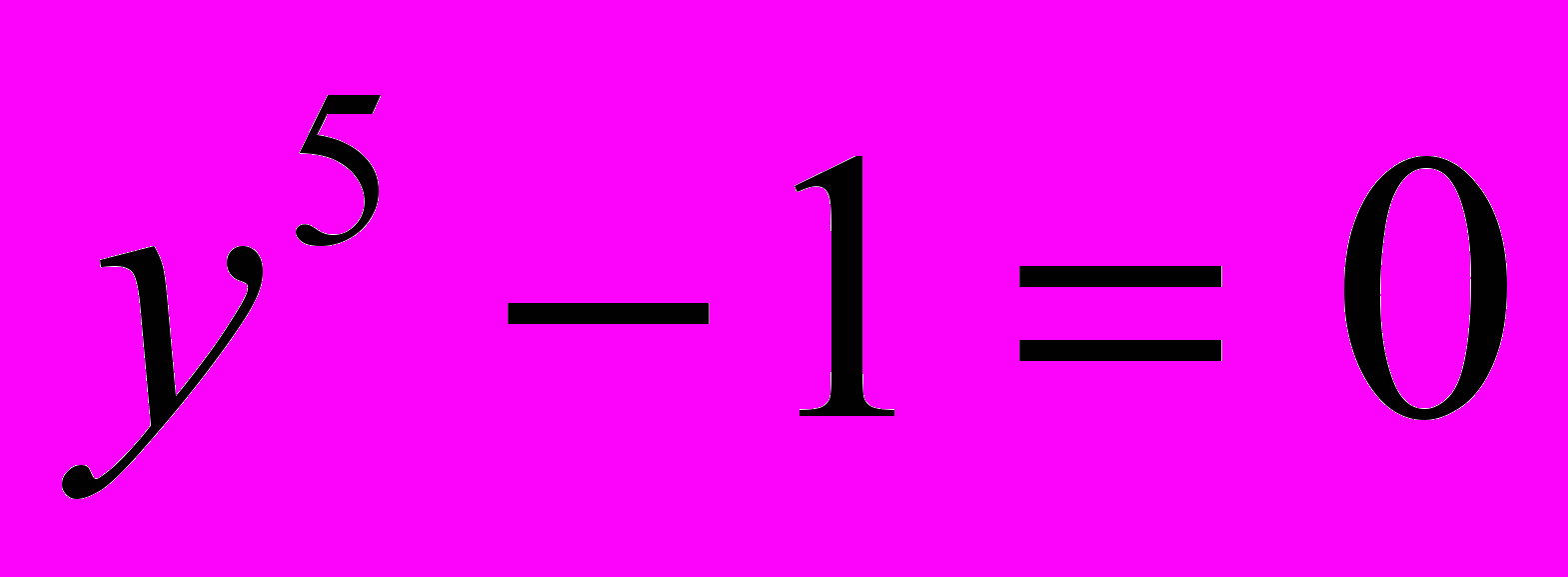8. Тест

1. Сумма корней уравнения равна
   

1) 4 2) 5 3) -3 4) 6 5) 7

2.Найдите наименьший корень уравнения(х+2)(

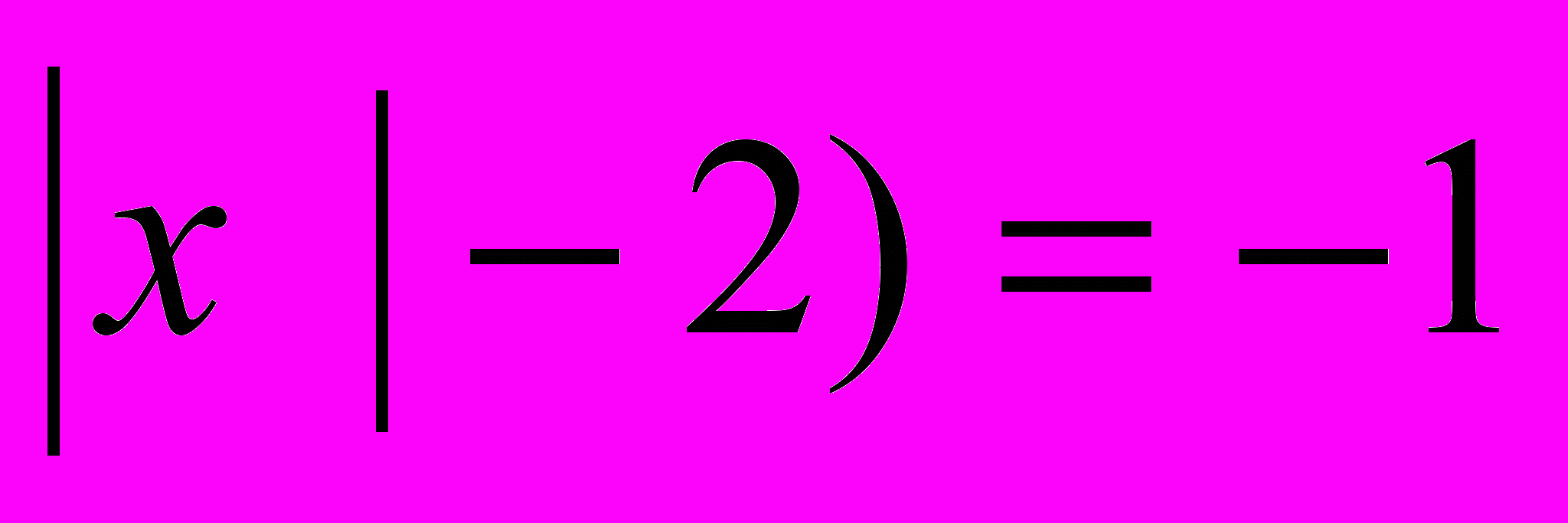
1) 4 2) 1 3) -2 4) -3 5)-4.

3. Найдите произведение корней уравнения

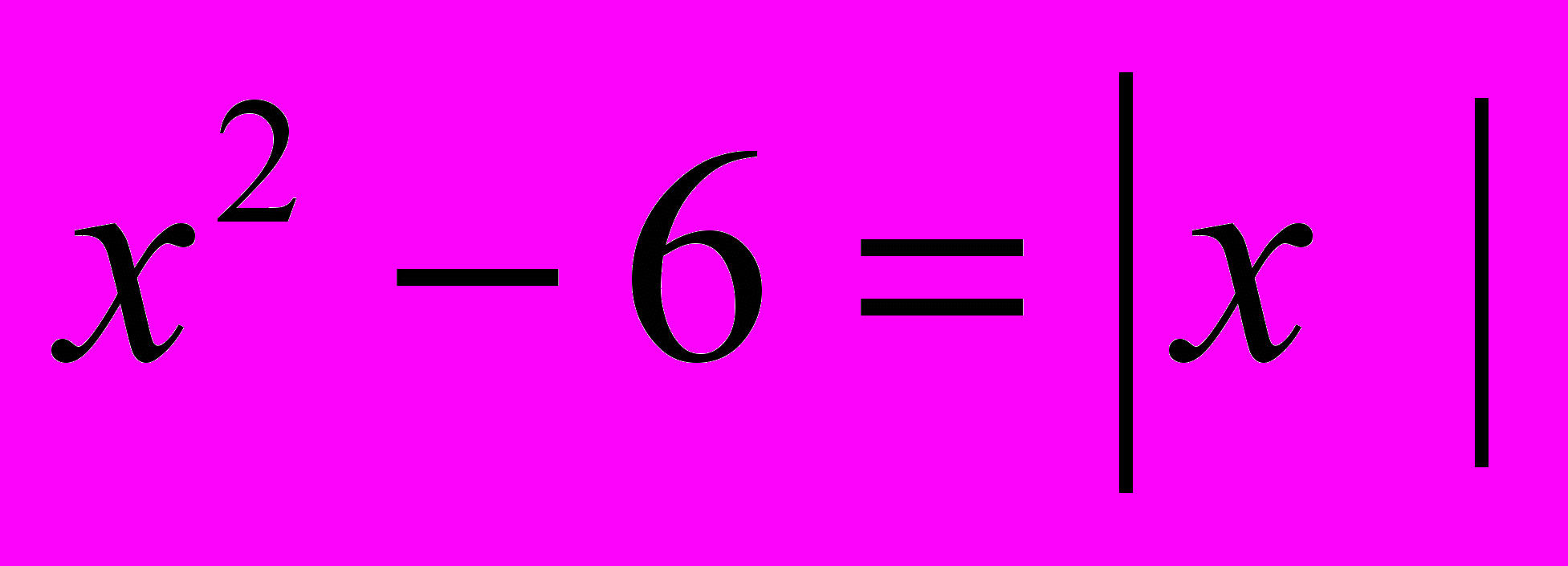
1) - 10 2) -9 3) -2 4) 5 5) 7

4.Сумма корней уравнения 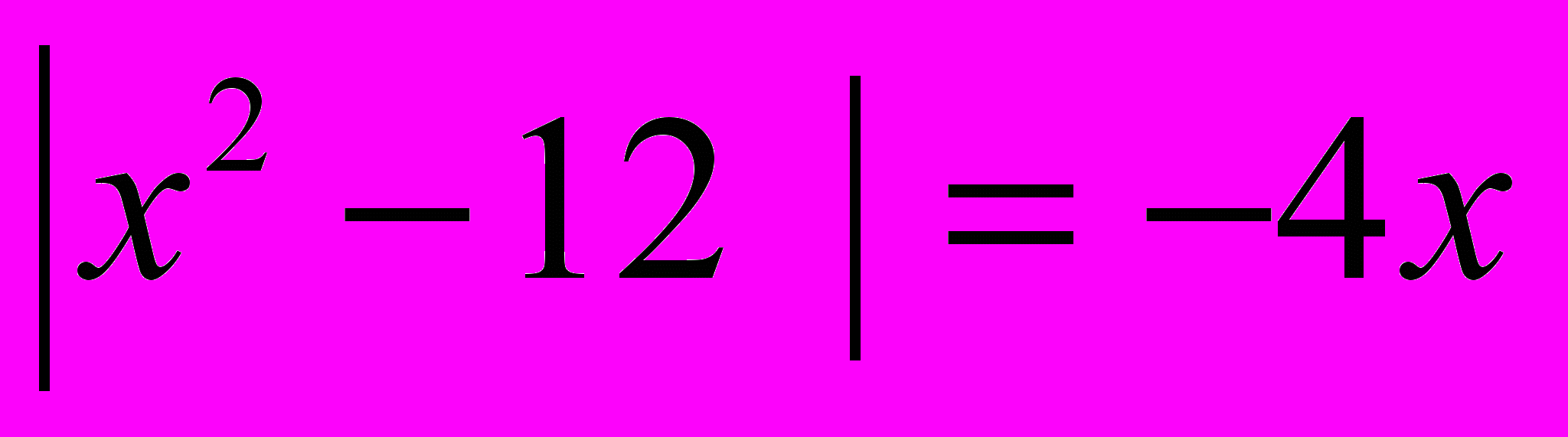равна

1) 8 2) -8 3)0 4)-4 5) 4.

5.Найти все значения параметра а, при котором графики функций у =

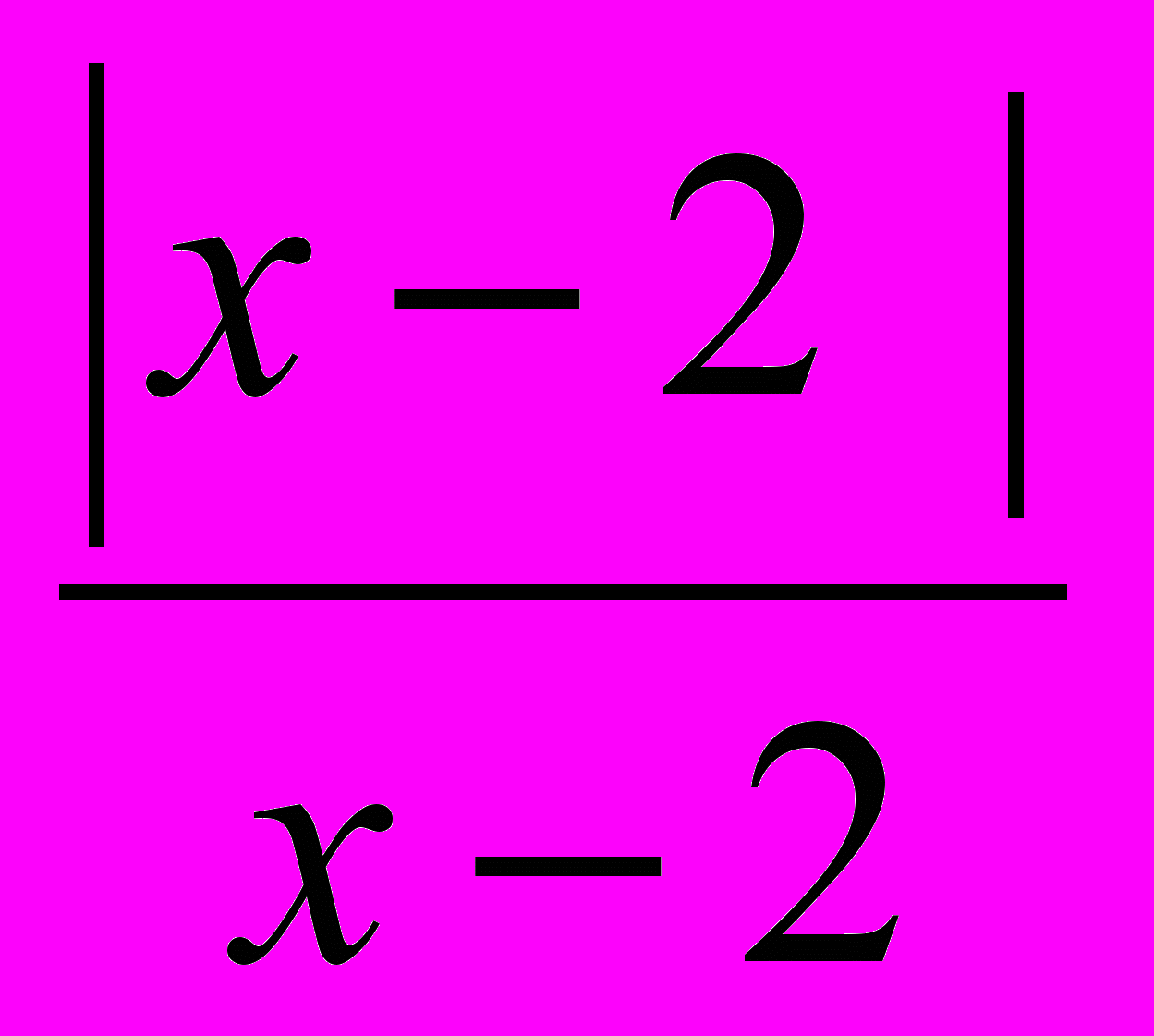
и у = 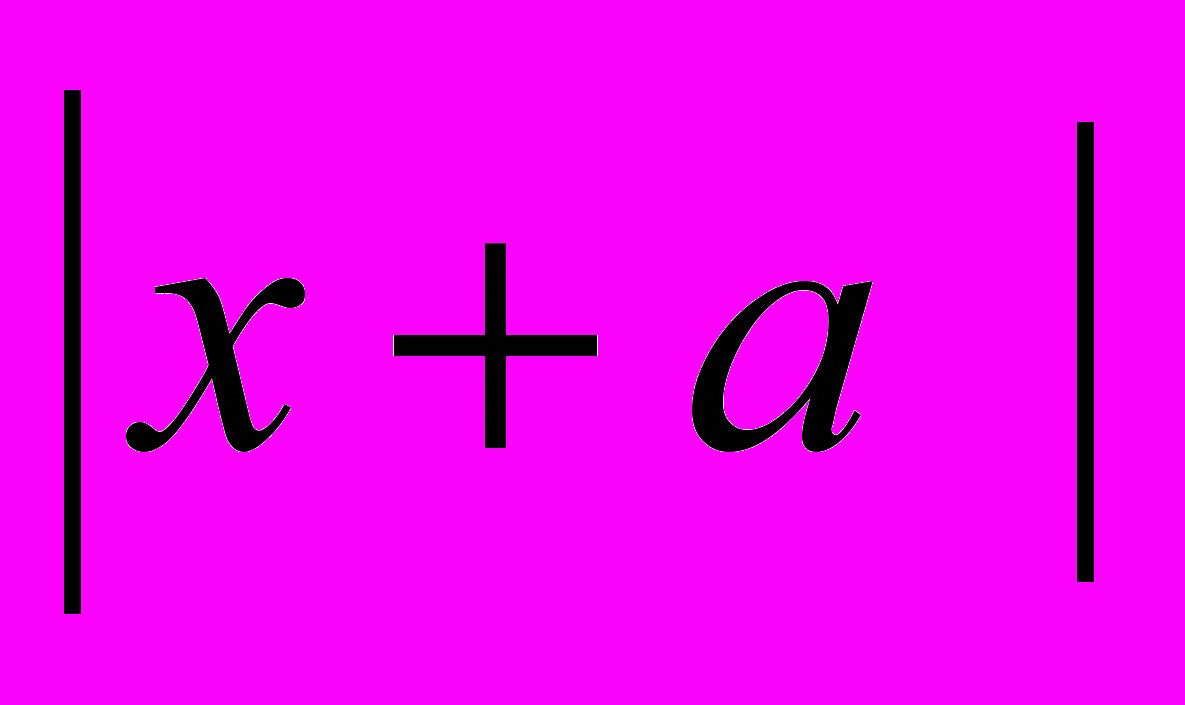имеют одну общую точку

1) (- ∞; -3) 2) (- ∞; -2) 3) [-3; -2) 4) [-2;-1] 5) [-3;-1)


9. Контрольная работа

Оценка	«3»	«4»	«5»
Основная часть	2	2	2
Дополнительная часть		1	2

Основная часть

1. При каких значениях параметра а уравнение 2а(а-2)=а-2 имеет решение?
   
2. При каких значениях параметра а уравнение ах(а+1)=а-2+6химеет решение? Сколько таких решений?
   
3. Решите уравнение .
   

Дополнительная часть

1. Найдите все значения параметра а, при которых корни уравнения

(а-1)х²+2ах+а+3=0 одного знака.

2. При каких значениях параметра а корни уравнения ах²-(2а+1)х+3а-1=0 больше 1?


Самостоятельная работа №10

Оценка	«3»	«4»	«5»
Количество баллов	7-9,5 баллов	11-15,5 баллов	16-21,5 баллов

Задания первой части оцениваются в 0,5 балла.










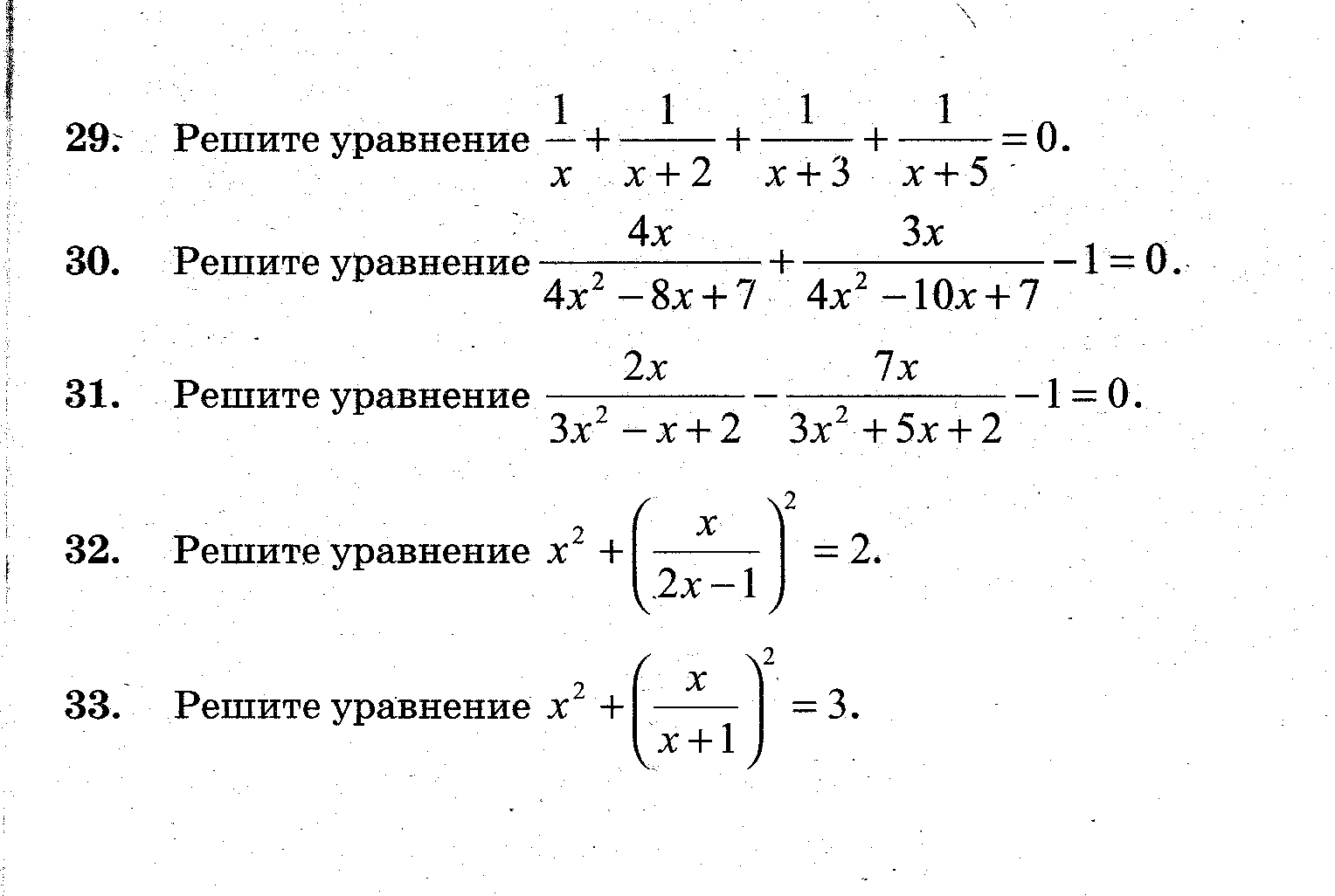
Для определения рейтинга данного элективного курса возможно проведение анкетирования


Приложение

Примерные вопросы анкетирования:

• Ваше отношение к курсу:
  
  1. Мне понравилось заниматься;
     
  2. Мне было трудно;
     
  3. Это точно не для меня;
     
  4. Другое ________________________________________________
     
     • С каким настроением Вы шли на данный курс? (поставьте «галочку» около соответствующего знака)
       
       • _______
         
         • _______
           
           • _______
             

• Считаете ли Вы, что цели данного элективного курса достигнуты?
  
  1. да;
     
  2. нет.
     
• Усвоили ли Вы главное в изученном курсе?
  
  1. да;
     
  2. нет.
     
• Научились ли Вы решать задачи по теме курса?
  
  1. да;
     
  2. нет.
     
• Составлен ли Вами опорный конспект по теме элективного курса, который будет использоваться в дальнейшем?
  
  1. да;
     
  2. нет.
     
     • Поставьте «галочку» около соответствующего знака, который отвечает Вашему настроению по окончании курса:
       
       • _______
         
       • ______
         
       • ______
         
         • _______
           
           • _______
             

Спасибо за ответы.