Кайгородова Людмила Николаевна, учитель математики, высшая квалификационная категория г. Бийск, 2008 г элективный курс

Вид материала

Элективный курс

Содержание Требования к знаниям и умениям учащихся Учебно – тематический план Содержание программы. Тема: Квадратный корень. Тема: Степень с целым показателем Тема: Квадратные уравнения. Тема: Неравенства. Методические рекомендации. Приложение. Разработка занятий. Процентная ставка Занятие №6. Занятие №7.

Подобный материал:

• Гусева Ольга Владимировна, учитель химии и биологии, высшая квалификационная категория, 158.84kb.
• Чулкова Марина Николаевна, учитель математики элективный курс, 67.8kb.
• Т. А. Аббясева «математика и сельское хозяйство» (Предпрофильный курс) Автор курса, 92.47kb.
• Сангаджиева Любовь Батовна, учитель физики, высшая квалификационная категория. Москва, 1226.42kb.
• План-конспект урока педагогическая мастерская «Кошки это кошки» Тема, 70.6kb.
• Разработчики рабочей программы: Голубева Г. П. учитель истории и обществознания сош, 479.43kb.
• Голубева Любовь Николаевна, учитель иностранного языка,вторая квалификационная категория., 679.04kb.
• Дурягина Галина Алексеевна, высшая квалификационная категория. Тема урок, 57.77kb.
• Щербинина Людмила Васильевна, учитель русского языка и литературы, первая квалификационная, 2047.11kb.
• Смирнова Любовь Васильевна, учитель математики, высшая квалификационная категория Утверждено:, 109.31kb.

Муниципальное общеобразовательное учреждение «Гимназия №11»


«Прикладные задачи в алгебре»

(программа элективного курса)


Разработала: Кайгородова Людмила Николаевна,

учитель математики,

высшая квалификационная категория


г. Бийск, 2008 г.


Элективный курс

«Прикладные задачи в алгебре»

Пояснительная записка

Элективный курс «Прикладные задачи в алгебре» предлагается учащимся 8 классов для предпрофильной подготовки.

Говоря о прикладных задачах, имеется ввиду приложение определенного раздела науки к внешней (по отношению к этому разделу) предметной области. Поэтому прикладной для математики является теоретическая задача, допустим из химии и физики.

Фабула задач основана на различных сферах человеческой деятельности, т.к. законы математики обязательны для всех наук. Круг ее приложений очень широк. С другой стороны, математика черпает идеи для своего дальнейшего развития именно из приложений.

Поэтому целью изучения данного элективного курса является: создание условий для формирования у учащихся:

• представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов;
  
• обобщения и систематизации знаний учащихся, полученных на уроках алгебры.
  

Задачи курса:

• расширить предметные комбинации математики и с другими предметами за счет практико – ориентированных приемов познавательной деятельности;
  
• формировать навыки работы со справочной литературой;
  
• развивать логическое и алгоритмическое мышление учащихся;
  
• способствовать формированию познавательного интереса к математике.
  

Актуальность изучения данного курса заключается в том, что он соответствует концепции модернизации образования: «Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений и навыков, а также опыт самостоятельной деятельности».

Требования к знаниям и умениям учащихся:

В результате изучения курса ученики должны:

Знать и понимать:

• значение математической науки для решения практических задач, применение математических методов к анализу и исследованию процессов и явлений в природе и обществе;
  
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности.
  

Уметь:

• решать задачи с применением рациональных дробей;
  
• использовать при решении задач квадратные уравнения;
  
• использовать неравенства при решении практических задач;
  
• решать практические задачи содержащие степень с целым показателем.
  

Учебно – тематический план

№	Наименование темы курса	Всего часов	В том числе			Конр.раб.	Форма контроля
			лекция	Практи- ка	творч. раб.
1	Рациональные дроби	6	1	4	1		Защита творческой работы
2	Квадратный корень	6	1	4	1		Контрольная работа
3	Степень с целым показателем	6	1	4		1	Защита творческой работы
4	Квадратные уравнения	6	1	4		1	Контрольная работа
5	Неравенства	6	1	4		1	Контрольная работа

Содержание программы.

Тема: Рациональные дроби

Эта тема изучается на базовом уровне в курсе математики. В рамках данного курса изучаются задачи по физике, «на работу», «на сплавы, смеси и растворы», а также задачи экономического содержания. Решение этих задач позволит выработать навык построения математических моделей задач практического характера.

Тема: Квадратный корень.

В рамках данного элективного курса кроме решения физических задач будут рассмотрены задачи геометрического содержания. Это позволит показать связь физики, математики, геометрии, а так же математические методы решения данных задач.

Тема: Степень с целым показателем.

В ходе изучения темы дети познакомятся с числовыми великанами, которыми можно выразить количественные отношения реального мира. В этом плане особенно важны задачи, содержащие реальные величины, например, задачи о Солнечной системе, планетах и других космических телах.

Тема: Квадратные уравнения.

При изучении этой темы существенно расширится круг посильных для учащихся прикладных задач как физических, геометрических так и экономических.

Тема: Неравенства.

Все величины измеряются с определенной погрешностью и их числовые значения заключены в некоторых пределах, следовательно при решении многих задач, в частности экономического, физического содержания, бывает достаточно грубой оценки искомой величины. Поэтому тема посвящена созданию ситуаций для приобретения учащимся навыков приближенных вычислений.

Методические рекомендации.

Учащиеся в ходе изучения курса имеют возможность составлять математические модели задач физического, экономического, геометрического содержания, а также задачи связанные с химией «на сплавы, смеси и растворы». Развитию креативности детей будет способствовать защита творческих работ.

Лучшему усвоению теоретического материала будет способствовать лекция, проблемная беседа. Ученики в ходе создания творческих работ будут самостоятельно выбирать объект изучения, литературу.

В целом, изучение курса поможет учащимся определиться с выбором профиля обучения.

Приложение. Разработка занятий.

Занятие №1.

Краткое содержание лекции.

Уравнение, которое необходимо составлять на основании условия этих задач, обычно содержит такие параметры движения, как пройденное расстояние (S,l,r), скорости движения тел (U,V,W), время движения (t,T). (Обозначение тех или иных неизвестных обычно принятыми для них в физике буквами. Концентрирует внимание на существе задачи, делает уравнение более понятным для решающего задачу, исключают случайные ошибки, которые могут возникнуть из – за безликости введенных обозначений).

Допущения, которые обычно принимаются (если не оговорено противное) в условиях задач "на движение", состоят в следующем:

а) движение на отдельных участках считается равномерныи при этом пройденный путь определяется по формуле:

S=Vt

б) повороты движущихся тел принимаются мгновенными, происходят без затрат времени; скорость при этом также меняется мгновенно:

в) если тело движется по течению реки, то его скорость w складывается из скорости в стоячей воде v и скорости течения реки и:

w = v + u,

а против течения реки его скорость равна

w = v - u.

Если в условии задачи речь идет о движении плотов, то этим хотят сказать, что тело движется со скоростью течения реки.

В задачах "на движение" полезно составить иллюстративный чертеж. Этот чертеж следует делать таким, чтобы на нем была видна динамика движения со всеми характерными моментами - встречами, остановками и поворотами. Хороший чертеж позволяет понять содержание задачи, не заглядывая в ее текст. Примеры таких чертежей приведены ниже.

При решении задач "на движение" часто встречаются следу­ющие два элемента:

а) движение навстречу друг другу: если первоначальное расстояние между двумя точками, движущимися навстречу друг другу со скоростями v₁ и v₂, равно s₀ то время, через которое они встретятся, равно





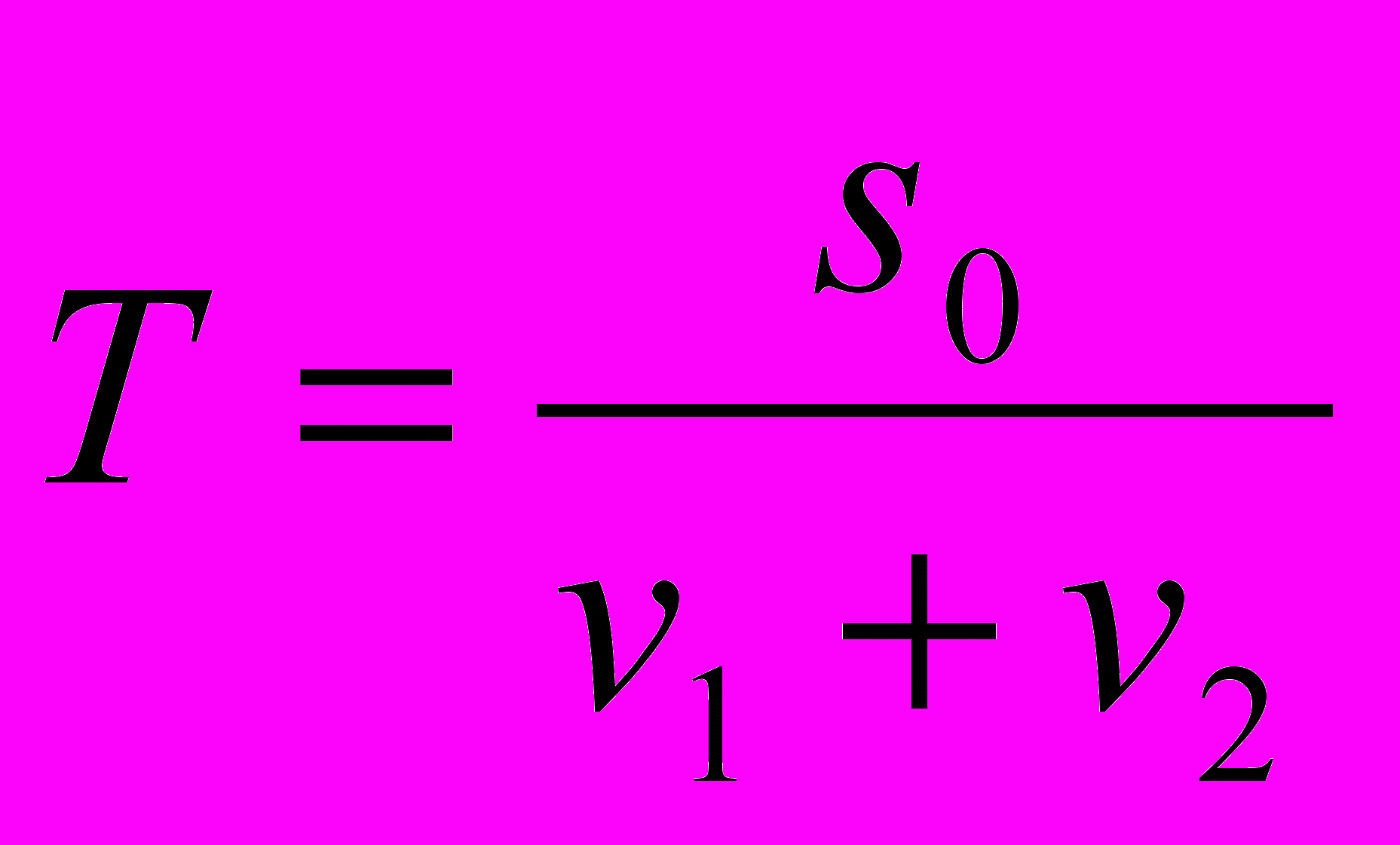
б) движение в одном направлении; если первоначальное расстояние между двумя точками из которых одна догоняет другую, равно s₀, то время, через которое вторая точка (скорость v₂) догонит первую (скорость V₁) равно



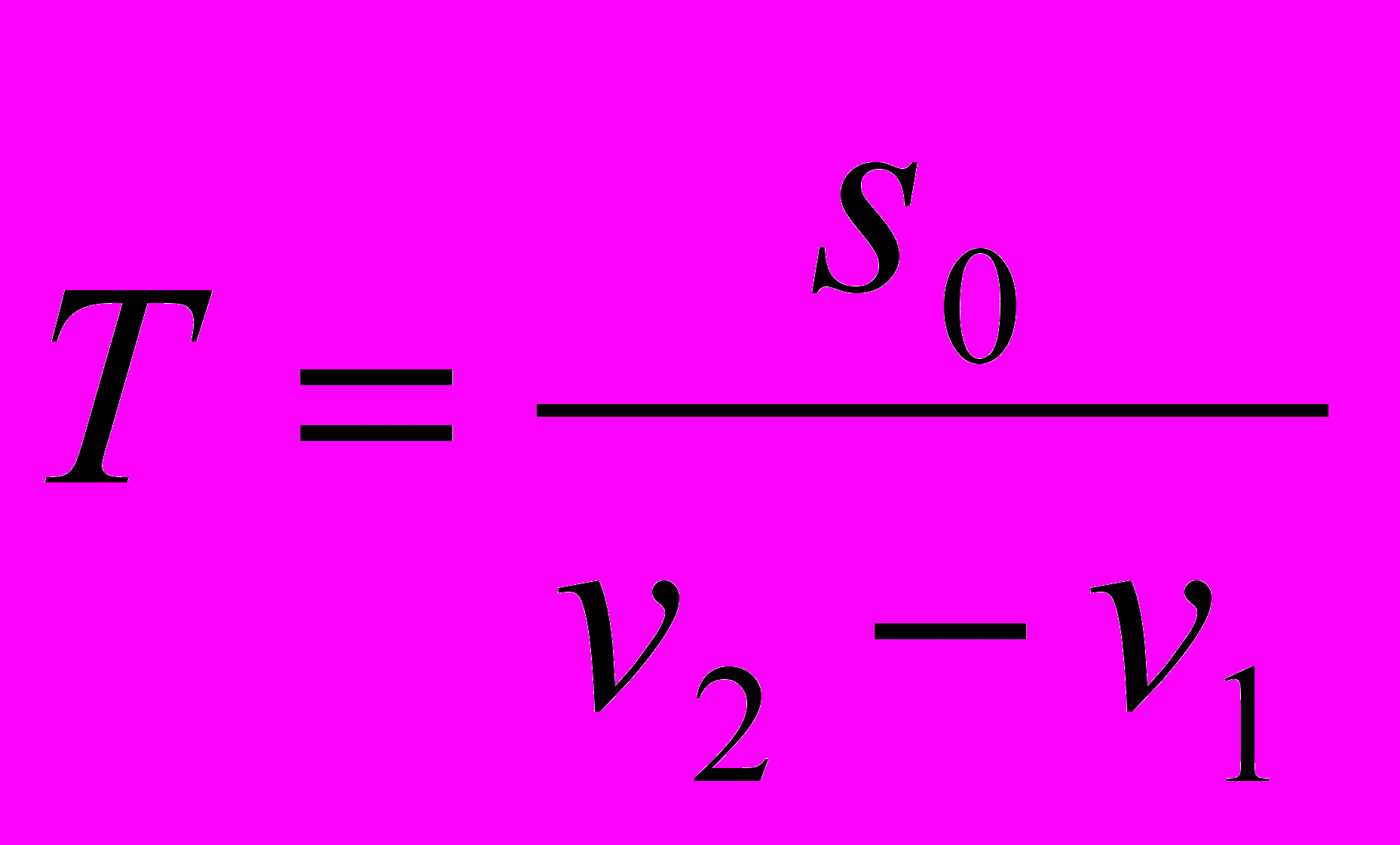(v₂>v₁)

Задача №1.

Расстояние между двумя городами равно s. Из первого города во второй отправились велосипедист и мотоциклист. Мотоциклист прибыл во второй город на t часов раньше. Какова скорость каждого, если скорость мотоциклиста в 5 раз больше, чем велосипедиста?

Задача № 2.

Из одного и того же пункта в одном и том же направлении отправляются Чебурашка со скоростью u км/ч и через t часов крокодил Гена со скоростью v км/ч. Через сколько часов Ге­на догонит Чебурашку?

Занятие №2

Задача №1.

Расстояние между Чебурашкой и крокодилом Геной бы­ло s_b когда они направились навстречу друг другу, причем Гена шел вдвое быстрее Чебурашки. Через час расстояние между ними стало s₂. Какова скорость Чебурашки?

Задача №2.

В механических часах много зубчатых колес. Пусть два
из них составляют зубчатую передачу: у первого п зубцов, у вто­рого т (m>n). Одно колесо делает в минуту на k оборотов боль­ше другого. Сколько оборотов в минуту делает каждое колесо?

Задача №3.

Выведите формулу, которая выражает зависимость пути, пройденного комбайном до заполнения бункера зерном, от урожайности убираемой культуры. Обозначьте: V — объем бункера (ц), у — урожайность (ц/га), а — длина пути (м), b - ширина захвата жатки (м).

Занятие №3.

Задачи на совместную работу

Между величинами, описывающими равномерное движе­ние и величинами, характеризующими процесс работы име­ется полная аналогия. Представим это в виде таблицы.

Движение	Путь — S	Время движения —t	Скорость движения
Работа	Вся работа — А	Время работы — t	Производитель­ность

Существенное отличие между этими типами задач:

• при совместной работе нескольких объектов, выполняющих одновременно работу, их общая производительность является суммой производительностей отдельных объектов;
  
• во многих задачах на работу точный характер этой работы не определен, тогда удобно принять объем всей работы за единицу и измерять часть такой работы в долях от единицы.
  

Задача №1.

Винни-Пух и Пятачок выполняют совместную работу. Один Винни-Пух может ее выполнить за t₁ часов, а Пятачок — за t₂ часов. За какое время они выполнят работу вместе?

Задача №2.

Завод планировал выполнить заказ за t_t дней, но, выпуская на п изделий в день больше запланированного, справился с заказом за t₂ дней. Сколько изделий выпускалось в день?

Занятие №4.

Краткое содержание беседы:

1. Что называется процентом?
   

(Процентом называется сотая часть числа, обозначается %).

2. Представьте в виде десятичной дроби:
   

35%; 40%; 75%

3. Как найти процент от числа.
   

(Чтобы найти a% от числа b, надо число b умножить на )

4. Как найти число по его процентам?
   

(Если известно, что a% числа x равно b, то число x можно найти по формуле )

5. Как найти процентное отношение двух чисел?
   

(Чтобы найти процентное отношение двух чисел a и b, надо отношение этих чисел умножить на 100%, т.е. вычислить )

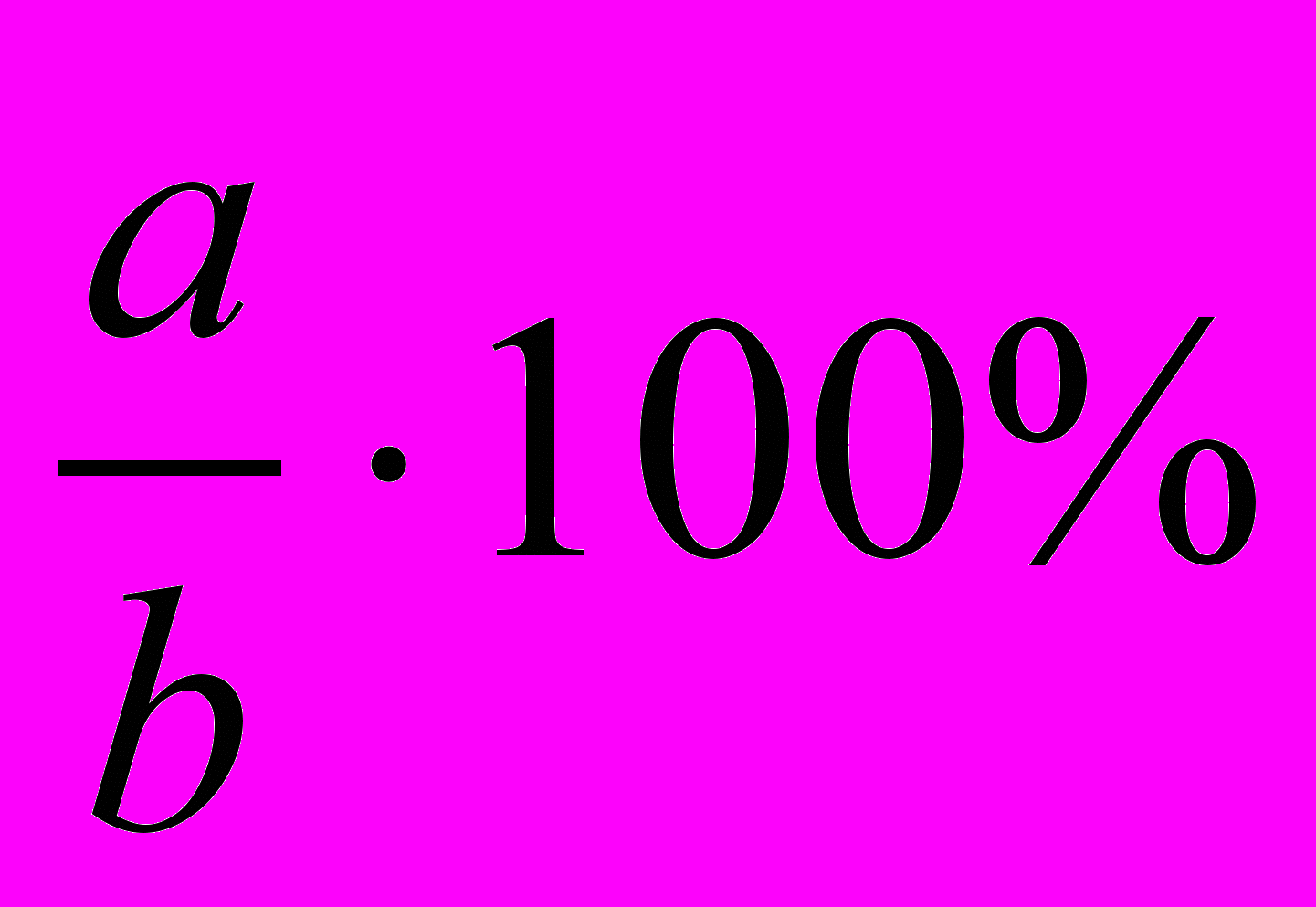Решение задач на процентный прирост основано на использовании следующих понятий и формул. Если некоторая переменная величина в начальный момент имеет значение Y₀ и затем возрастает на p %, то это означает, что ее значение увеличивается на величину 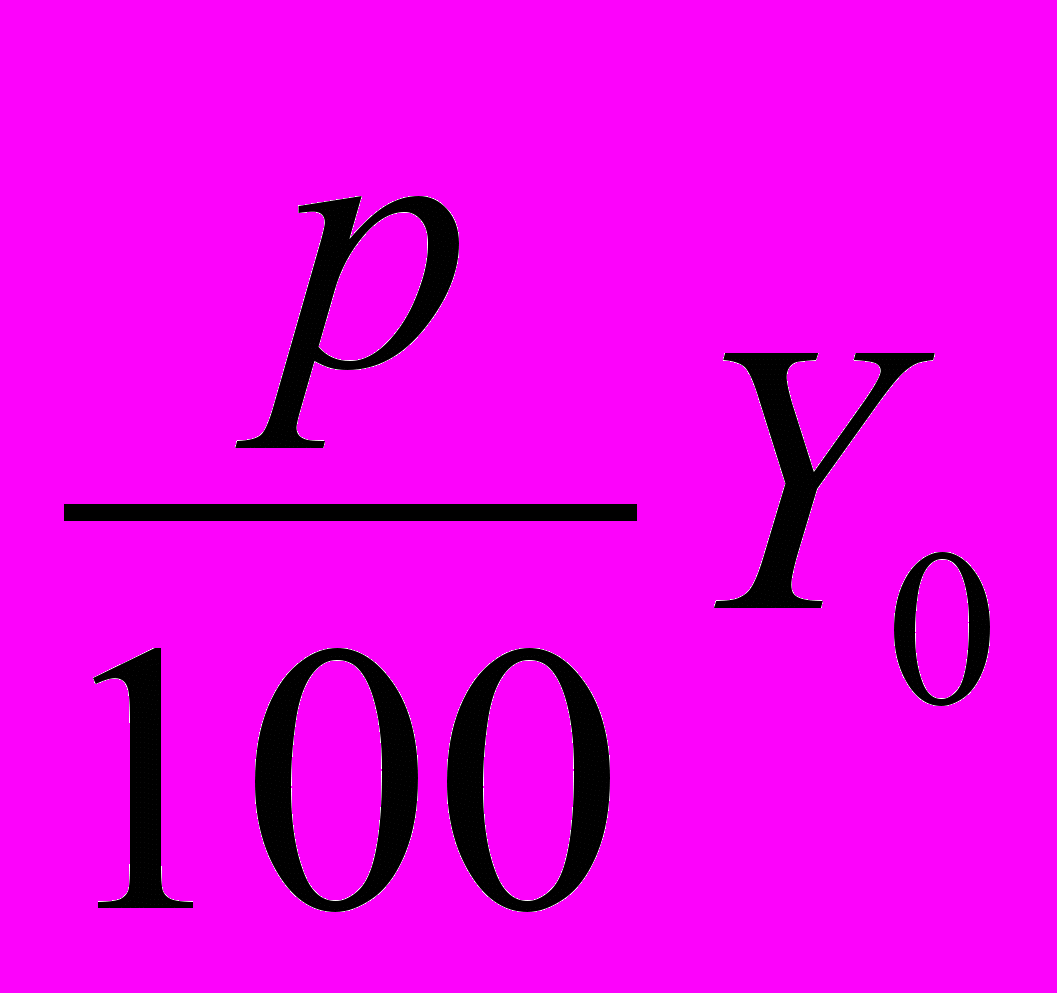, т.е. становится равной . Если новое значение Y₁ увеличивается еще на q%, величина становится равной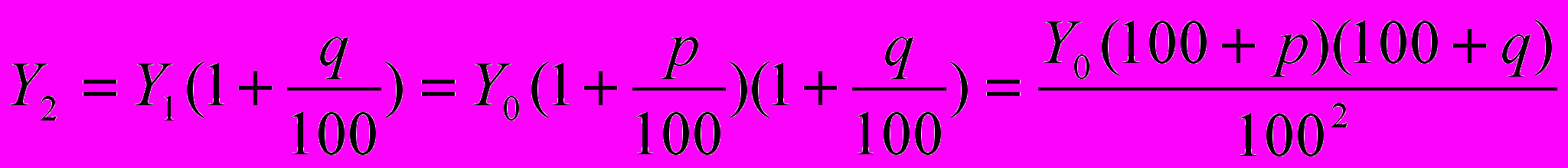



Примечание: если значение величины уменьшается, то в формуле стоит знак минус.

Задача №1.

Зарплата была 200 денежных единиц. Ее повысили на 20%, а новую понизили на 20%. Сколько денежных единиц составляет зарплата?

Задача№2.

Цена понизилась на 20%, затем еще на 30% и еще на 50%. Насколько всего процентов понизилась первоначальная цена?

Задача №3.

Кредит в 10 млн. р. получен на год с условием уплаты 120%. За год инфляция составила 100%. Каков доход кредитора?

Задача №4.

Кредит на сумму С получен под ссудный процент 100р%. За год инфляция составила 100i%. Какую прибыль получил кредитор через год (в процентах)?

Справка. Кредит (ссуда) – предоставление денег в долг с условием вернуть в срок с процентами.

Процентная ставка называется ссудным процентом.

Кредитор тот, кто дает ссуду; дебитор – должник.

Инфляция – обесценивание денег и рост цен.

Занятие №5.

Задачи на сплавы и смеси

В задачах на смеси можно выделить несколько приемов, удобных для их решения.

1. В некоторых задачах со смесями рассматривается смесь двух веществ. При этом количество одного из веществ смеси изменяется, а другого — остается постоянным. При этом обычно в условии сообщается доля, которую составляет в смеси меняющееся вещество. В таких задачах удобно пересчитать сначала долю неизменного вещества и при составлении уравнения использовать неизменность количества этого вещества в процессе преобразования смеси. Часто такой метод называют методом «сухого остатка».

2. Если в задаче идет речь о смешивании нескольких различных смесей, каждая из которых включает одни и те же вещества, то бывает удобно разделить исходные смеси на составляющие их вещества - компоненты и учитывать что итоговой смеси количества этих компонентов складываются из количеств в исходных смесях.

3. Если со смесью двух веществ последовательно производят несколько действий, то бывает удобно отслеживать количество одного из веществ в смеси после каждого из совершаемых действий. Для такого отслеживания часто используют понятие концентрации вещества в смеси, то есть вычисляют какую массовую или объемную долю составляет дан вещество. Говоря о смесях, растворах и сплавах, будем употреблять термин «смесь»;

- смесь состоят из «чистого вещества» и «примеси». Что есть «чистое вещество», определяется в каждой задаче отдельно, при этом все остальные вещества, составляющие смесь, относятся к примеси;

-долей (а) чистого вещества в смеси называется отношение количества чистого вещества (m) в смеси при условии, что они измерены одной и той же единицей массы или объема: 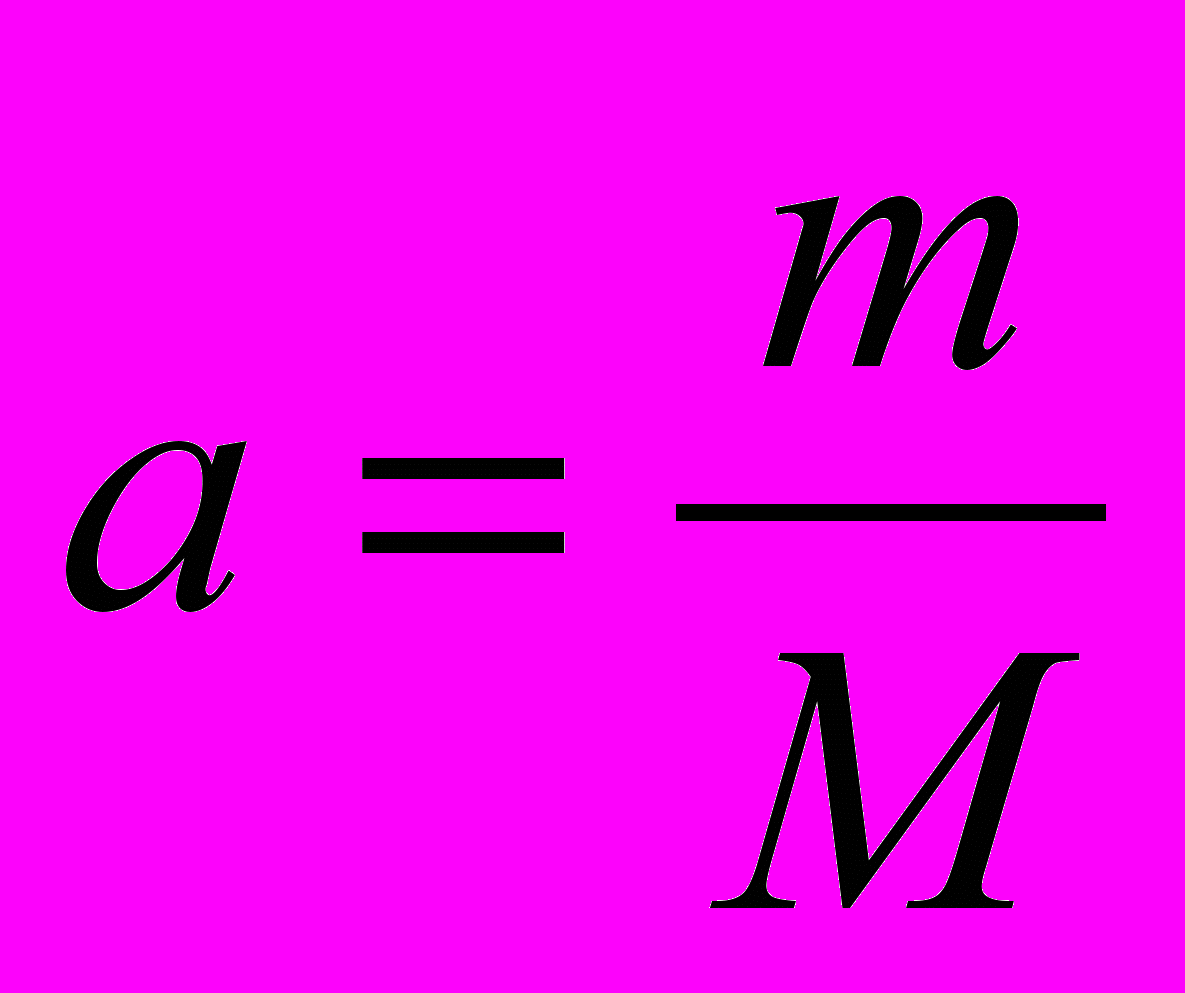, тогда , где 0≤a≤1. Условная запись:

;

- процентным содержанием чистого вещества смеси (с) называют его долю, выраженную процентным соотношением: .

Задача №1.

Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?

Задача №2.

Сколько воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?

Задача №3.

От двух сплавов соответственно массой 7 кг и 3 кг с разным процентным содержанием магния отрезали по куску одинаковой массы. Затем, кусок, отрезанный от первого сплава, сплавили с остатком второго сплава, а кусок, отрезанный от второго сплава, сплавили с остатком первого сплава. Определить массу каждого из отрезанных кусков, если новые сплавы получились с одинаковым процентным содержанием магния.

Занятие №6.

Задача № 1.

Взяты два сплава, содержащие Р₁ и Р₂ процентов меди. В результате их сплава получился металл с P-процентным содержанием меди. Первого сплава взято m₁ килограммов. Сколько было взято второго сплава?

Задача №2.

Имеется два раствора соды разной концентрации. В литр первого раствора влили k литров второго раствора. Получился раствор с концентрацией Р. А когда в литр первого раствора влили т литров второго, получили раствор концентрации С. Какова концентрация исходных растворов?

Задача №3

В сосуде 200 г раствора, в котором содержится 12 г соли. В него поступает чистая вода со скоростью 1 г/мин. Через какое время концентрация соли в растворе уменьшится в 3 раза?

Защита задач, составленных учащимися по данной теме (в форме докладов, презентаций).

Занятие №7.

Задача №1

Кирпич падает с высоты 1 м. С какой скоростью он упа­дет ни землю? Во сколько раз увеличится скорость, если высота увеличится в 2, 4, 100 раз? Справка. Скорость свободного падения тела выражается формулой 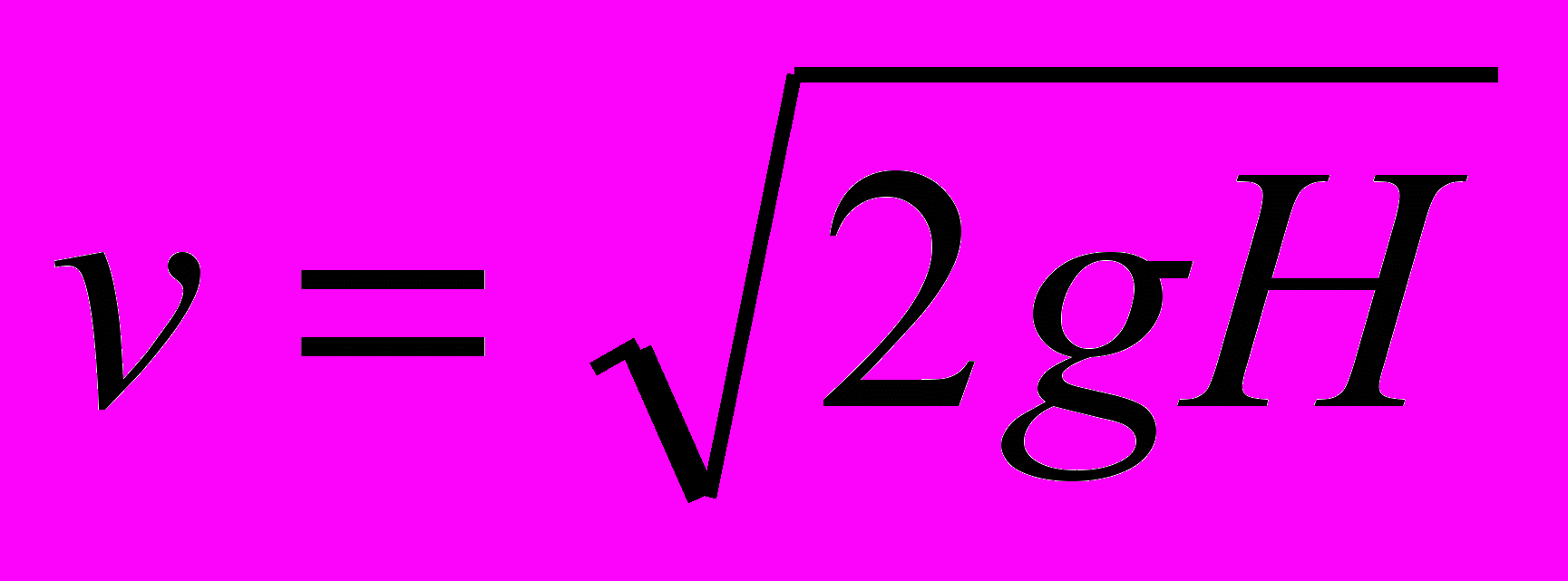, где H — высота, g — ускорение свободного падения, g = 9,81 м/с².

Задача №2.

Чебурашка отправился в кругосветное путешествие на фантастическом корабле «Змей Горыныч», который за первый час проплывает 100 миль, а за t часов— 100 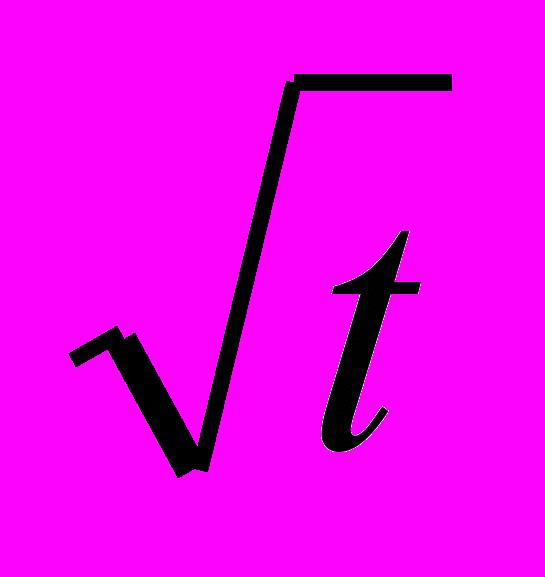миль (t>1). Крокодил Гена отговаривает Чебурашку:

• Давай лучше переходи ко мне на «Черепаху». Дольше путешествовать будем.
  
• А какая у нее скорость?
  
• Один узел.
  
• Что, в час всего одна миля? Нет, это уж слишком медленно.
  

Друзья поплыли маршрутом Магеллана. Каждый на своем корабле. Кто из них дольше был в пути? Насколько? Справка. 1 узел = I морской миле/ч, I морская миля = 1,852 км. Кругосветный путь — около 28 000 миль.

Указание. Измерьте кругосветный путь на глобусе. Для решения задачи построите графики функций s=100 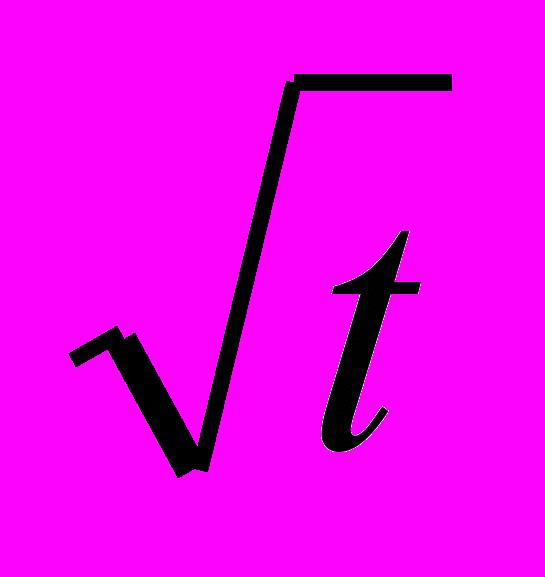и s =t.

Замечание. Фантастичность первого корабля в том, что при законе движения s=100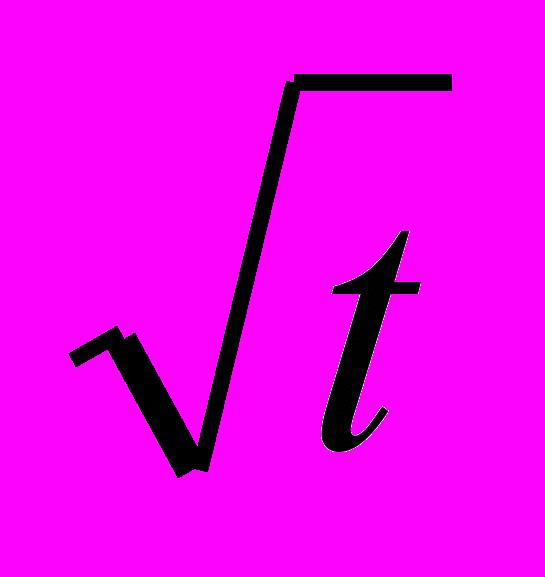' в начальный момент не определена скорость. Ученик сможет доказать это, когда будет учиться в 10-м классе, а сейчас он может убедиться, вычисляя скорость при очень малых значениях t, что она довольно велика. Поэтому в тексте задачи общий закон движения вступает в права только после первого часа, а за первый час просто дано пройденное расстояние.

Чтобы снять эту оговорку, надо изменить условия задачи, взяв другой закон движений, например s=100().

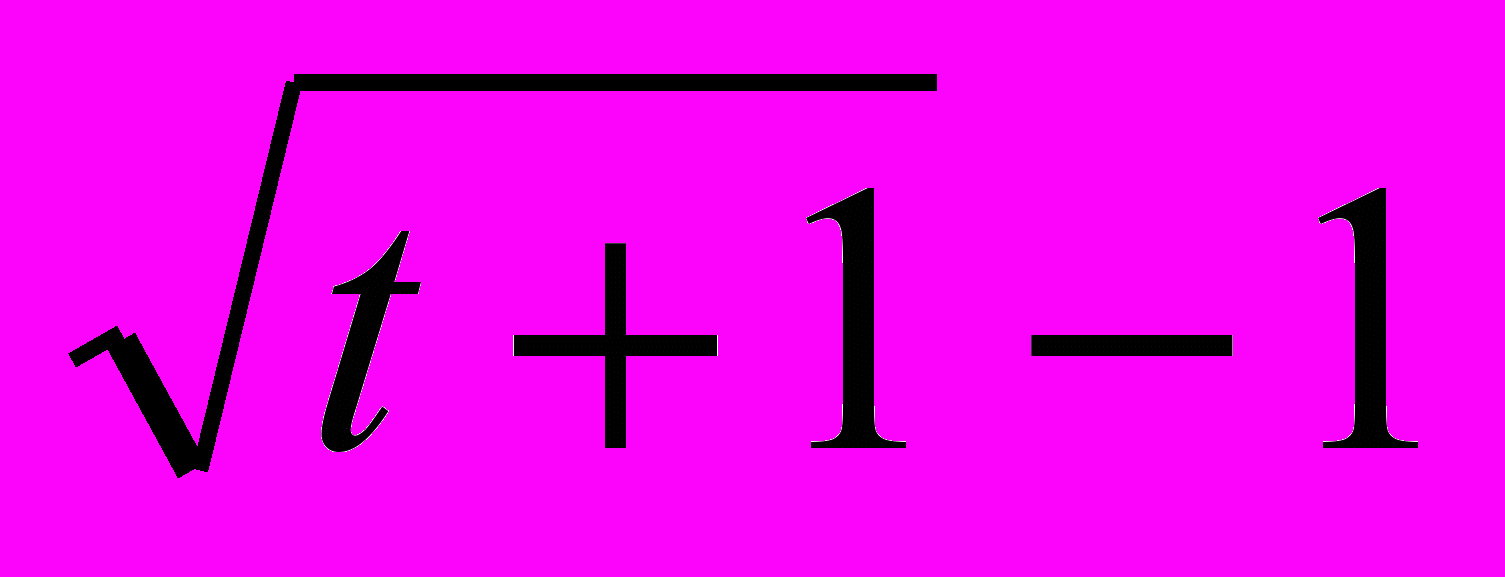Задача №3.

Крокодил Гена плывет на корабле «Черепаха» со скоростью пол-узла и хочет догнать Чебурашку, который на корабле «Змей Горыныч» покрывает миль за t часов. Удастся ли ему это?

Указание. Решите задачу графически, построив графики функций

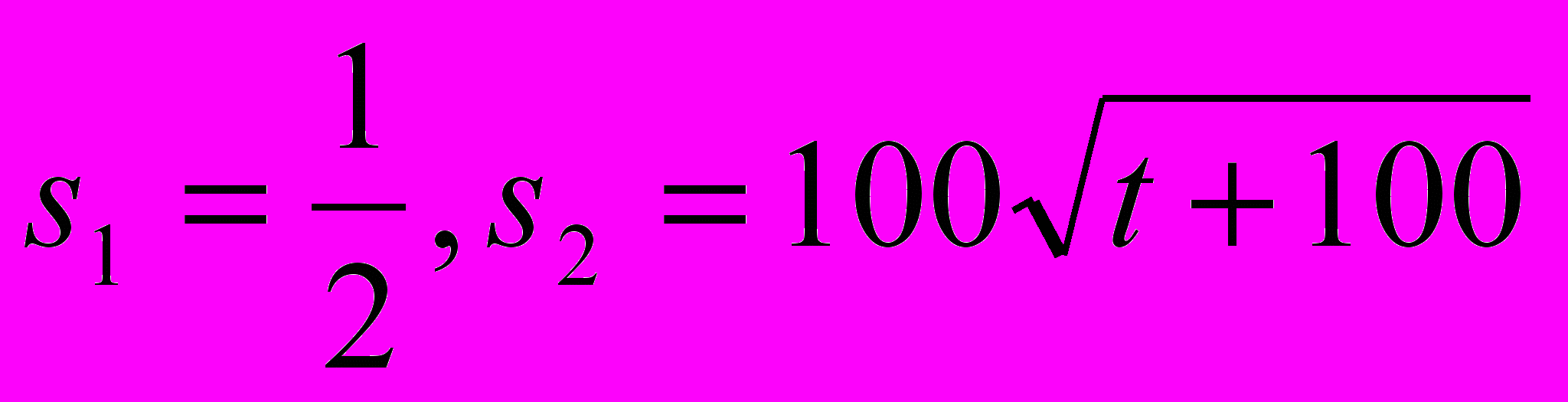
Задача №4.

Период Т качания математического маятника равен 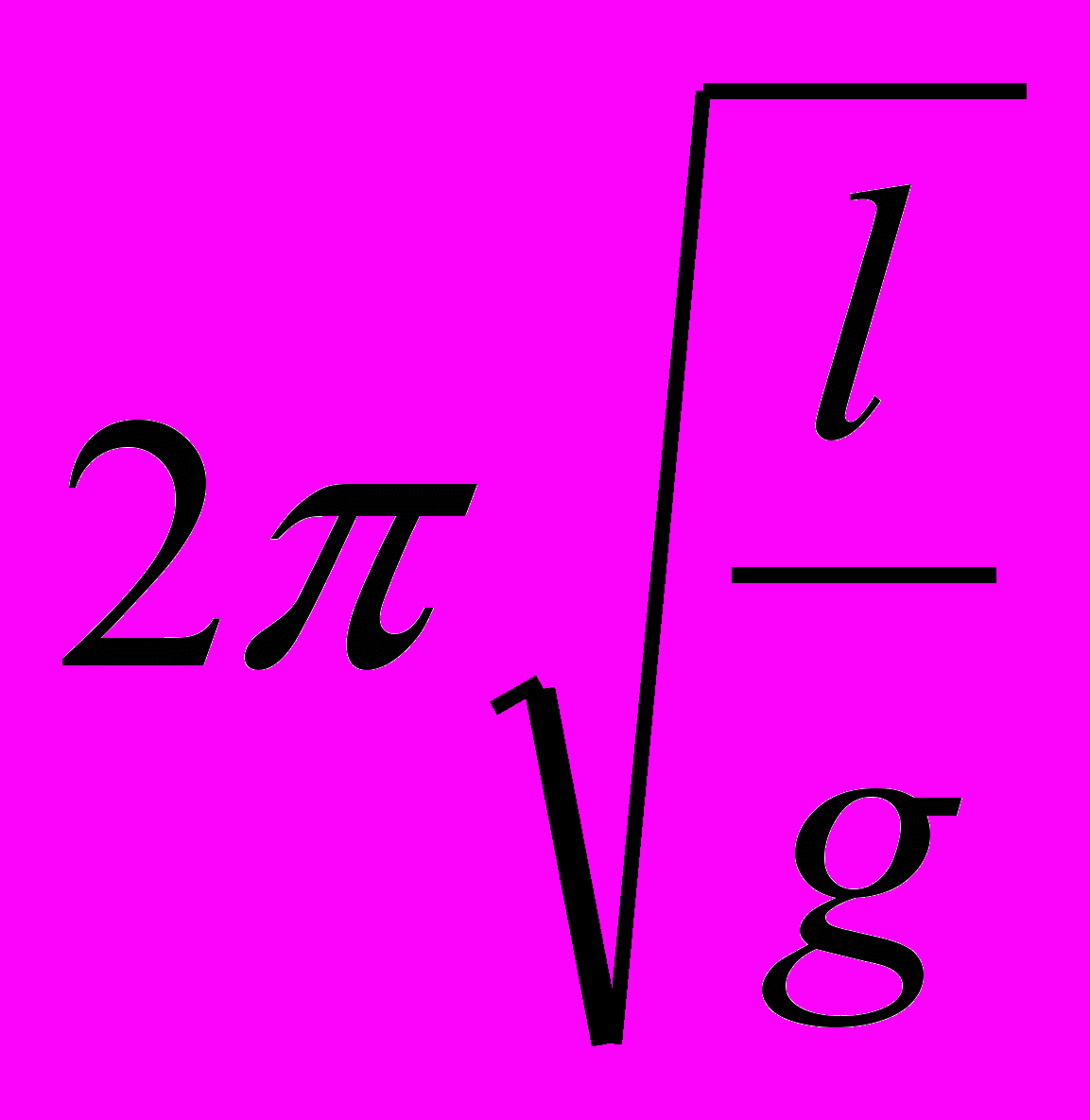где l — длина маятника, g — ускорение свободного падения. Сравните периоды качания у маятников, длины которых относятся как 4:1.

Занятие №8.

Задача №1.

Имеется кусок картона в форме прямоугольного треугольника. Длина одного из катетов равна 15 см. Какой длины должен быть второй катет, чтобы из треугольника можно было вырезать квадрат площади S? Решите задачу в общем виде, вычислите катет при s=1 дм².



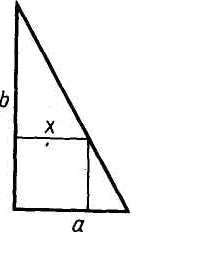
Задача №2.

Арка моста имеет форму параболы, заданной функцией y=0,04(100-x²). Высота ее 4 м, ширина основания 20 м. Под ней проходит плот с грузом в контейнере. Найдите зависимость максимально возможной ширины контейнера от его высоты. Вычислите ширину контейнера, если его высота 3 м.



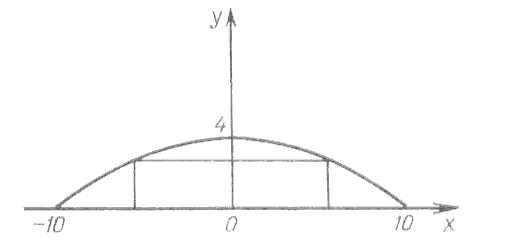
Задача №3.

Царь Салтан строит крепость в форме круга площадью в одну квадратную версту. И думает: какой же длины будет крепостная стена? На сколько короче эта стена по сравнению со стеной квадратной крепости с той же площадью?

Задача №4.

Царь Салтан решил построить еще одну крепость — на этот раз на берегу моря и в форме полукруга с площадью в две квадратные версты. Какова на этот раз длина крепостной стены? Намного ли она длиннее, чем у круглой крепости с вдвое меньшей площадью (см. предыдущую задачу)?



Занятие №9.

Задача №1.

Выведите формулу зависимости дальности горизонта СК от радиуса Земли R и высоты глаза наблюдателя H. Дальностью горизонта называют расстояние, на которое мог бы видеть глаз человека из точки С, если бы видимость зависела только от выпуклости земли и не зависела от состояния атмосферы, рефракции и других условий (бывают случаи, когда вследствие атмосферной рефракции виден предмет, например корабль, находя­щийся ниже видимого горизонта).



Задача №2.

Вычислите длину открывающихся горизонтов при подъеме на высоту 1 км. Какой горизонт открывается перед наблюдателями, поднявшимися на стратостате на высоту 19 км? Радиус Земли 6371 км. Вычислите дальность горизонта, открывающегося перед Ю. А. Гагариным во время его полета на космическом корабле «Восток», когда он находился в апогее (наибольшее расстояние) и в перигее (наименьшее рас­стояние) орбиты движения корабля, если известно, что высота перигея составляла 181 км, а апогея 327 км. Ра­диус Земли 6371 км.

Задача №3.

С самолета, находящегося на высоте 1,2 км над поверхностью Земли, опытный наблюдатель может видеть отдельные предметы, находящиеся на поверхности Земли на расстоянии 127,5 км. Определите по этим данным значение радиуса Земли.

Занятие №10.

Задача №1.

Население России с 1995 по 1997 г. уменьшилось от 148,7 млн. до 147,3 млн. человек. Оцените, на сколько процентов в год уменьшалась численность населения.

Задача №2.

Население Земли с 1993 по 1997 г. выросло от 5,55 млрд. до 5,88 млрд. человек. Оцените ежегодный прирост населения. Сделайте прогноз о численности народонаселения Земли на2000 г. (в предположении, что процент прироста постоянен).

Задача №3.

Отец с сыном-восьмиклассником сгребли сено и хотят метать стог.

• А что, сын, тут кубометров 25, наверное, будет. Давай для удобства будем считать 24. Какое же заложить основание стога в обхвате?
  

• А высота?
  

• Положим на перекидку метров 12, и считай!
  

Справка. Для приближенного вычисления объема стога V (м³) ис­пользуется формула 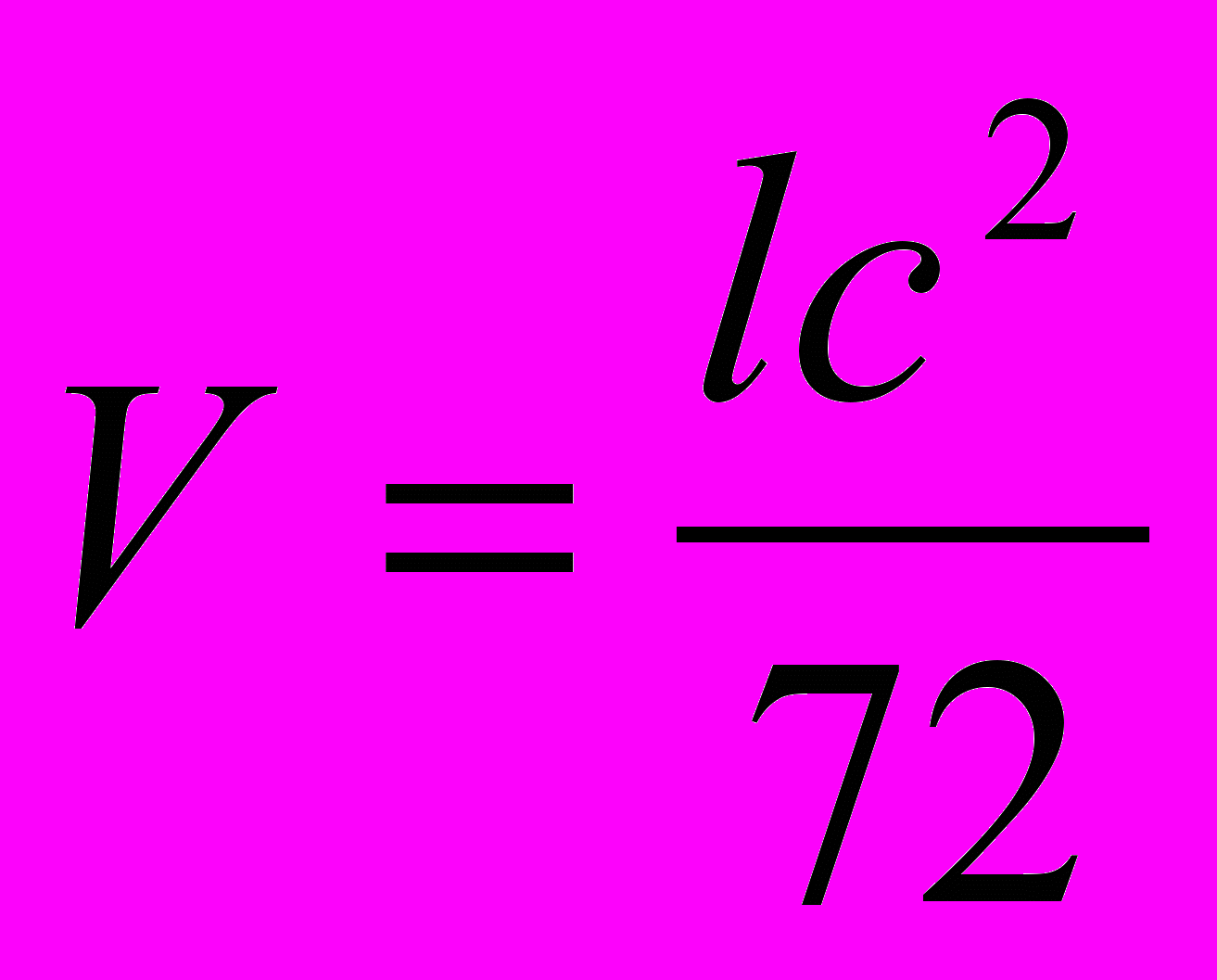, где c (м) – длина окружности в основании стога, l (м) – перекидка, т.е. длина перекинутой, через вершину веревки, оба конца которой лежат на земле.

Задача №4.

Горючее хранят в цилиндрических резервуарах, лежащих горизонтально. С поверхности горючего происходит испарение (за месяц примерно 4,8 кг с м²), поэтому ее называют «зеркалом испарения». Найдите формулу для вычисления площади «зеркала испарения», если известны длина цилиндра l, диаметр основания d = 2r и глубина слоя горючего h . Вычислите потери горючего за месяц при хранении его в цистерне с l = 6 м, d = 2 м, h = 1,8 м.



Литература:

1. Варданян С.С. Задачи по планиметрии с практическим содержанием: Кн. для учащихся 6-8 кл. сред. шк. / под ред. В.А. Гусева. – М.: Просвещение, 1989.
   
2. Математика для поступающих в десятый лицейский класс: Варианты конкурсных заданий: Учебное пособие / под общ. ред. В.Я. Райцина; сост. Л.А. Приходько. – М.: Издательство «Экзамен», 2006;
   
3. Новик И.А. и др. Задачи по математики: Кн. для учащихся / И.А. Новик, Н.К. Пещенко, Н.В. Бровка. – Мн.: Нар. асвета, 1984;
   
4. Фоминых Ю.Ф. прикладные задачи по алгебре для 7- 9 классов: Кн. для учителя. – М.: Просвещение, 1999;