Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный курс

Вид материала

Содержание

Формы и методы обучения.
Цель предлагаемого курса
Учебно-тематический план
Содержание программы.
Тема 2. Эйлеров и Гамильтонов циклы. Задачи о мостах. Рисование фигур единым росчерком.
Тема 3. История лабиринтов.
Тема 4. Задача четырех красок.
Тема 5. Графы с цветными ребрами и их свойства.
Тема 6. Понятие дерева в теории графов.
Тема 7. Графы и логические задачи.
Тема 8. Сетевые графы.
Тема 9. Применение теории графов в различных областях науки и техники.

Подобный материал:

МОУ СОШ № 49 г. Липецка

Учитель Тарасова Светлана Васильевна.

Предмет – математика.

Класс – 9

Элективный курс «Теория графов» (в рамках предпрофильной подготовки учащихся 9 класса).

Пояснительная записка.

За душу каждого математика борются демон абстрактной алгебры и ангел чистой топологии.

Андре Вейль.

…И не кричи мне, геометр,

что это все не топология

и речь в ней вовсе о другом.

Уймись! Тебя поймут немногие,

меня же – чуть не все кругом.

Л. Мартынов «Топология»

Предлагаемый курс является предметно-ориентированным. Его цель – подготовить учащихся к осознанному выбору сферы деятельности, а также познакомить учащихся с теорией графов, показать ее практическую направленность и применение в жизни. Прикладная направленность математики определяется тем, что без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация научных знаний, а также разнообразной социальной, экономической и политической информации.

Каждому человеку в жизни приходится выполнять достаточно сложные расчеты, пользоваться вычислительной техникой, владеть практическими приемами геометрических измерений и построений, читать информацию представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы.

И, наконец, все больше специальностей требующих высокого уровня образования связано с применением именно прикладной математики. Таким образом, расширяется круг школьников, для которых математика становится особенно важным предметом.

Для жизни в современном обществе важно формирование математического мышления, проявляющегося в определенных умственных навыках. Ведущая роль принадлежит формированию алгоритмического мышления и умения действовать по заданному алгоритму.

Изучение прикладной математики способствует эстетическому воспитанию человека, развивает воображение.

Важность математической подготовки прикладного назначения определяет следующие задачи обучения:

овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин;
интеллектуальное развитие учащихся, качеств мышления, характерных для математической деятельности;
формирования понимания значимости математики для научно – технического прогресса;
поддержание интереса у школьников к математике;
наделение учащихся применимыми на практике знаниями, формирующими и подкрепляющими уверенность в их математических способностях.

Темы, предложенные в данном курсе как таковые, не изучаются школьной программой. Но тема “Теория графов” имеет ярко выраженную, прикладную направленность. На простых примерах учащимся показывается, как можно применить язык теории графов к решению различных практических задач. Теория графов – развивающаяся область дискретной математики. Но методы теории графов завоевали признание не только математиков, но и инженеров, экономистов, психологов, лингвистов, биологов, химиков. Использование языка и методов теории графов часто ускоряет решение практических задач, упрощает расчеты, повышает эффективность научной, инженерной и конструкторской деятельности. Именно вопросы практики в значительной степени способствуют интенсивному развитию теории графов.

Учебный курс, излагающий основные положения теории графов, призван привлечь внимание школьников, интересующихся математикой.

Тема имеет ярко выраженную прикладную направленность. На простых примерах учащимся показывается применение теории графов к решению различных практических задач.

Своей простотой, доступностью и наглядностью язык теории графов поможет учащимся отвлечься от математических штампов. Теория графов успешно применяется при решении логических задач, графы помогают школьникам и при решении олимпиадных задач, которые требуют максимальной изобретательности при минимальных математических знаниях.

В последние десятилетия теория графов находит все новые области применения (физика, химия, генетика, психология, социология, экономика, лингвистика, электроника, теория планирования и управления). Именно запросы практики способствуют интенсивному развитию теории графов.

Кроме того, понятие «граф» очень емкое и связано со многими основными понятиями, на которых базируется математика, в том числе школьная.

Теория графов привлекательна и существованием нерешенных задач, в том числе имеющих традиционную занимательную форму.

Учащимся, заинтересовавшимся работой в области теории графов, предстоит решить множество увлекательных и интересных задач.

Поисковые и исследовательские задания будут способствовать формированию навыков самообразования, расширят знания в программных и внепрограммных областях.

Формы и методы обучения.

Наряду с традиционными формами и методами, в преподавании курса предусмотрено широкое применение таких форм занятий, как дискуссия, обсуждение, «мозговой штурм», «марафоны задач», деловые игры, круглый стол и пресс-конференция, лабораторно-графические работы. В преподавании курса опорными станут метод проектов (как учебных, так и творческих, научно-исследовательских), творческих и практических заданий по курсу.

Наряду с рефератами и докладами подразумевается подготовка научно-исследовательских работ как результата индивидуальной и групповой деятельности по итогам поисковой работы.

Цель предлагаемого курса – ознакомление на доступном уровне с одной из частей математического аппарата кибернетики, языком дискретной математики.

Задачи курса:

- развить интерес школьников к предмету;

- показать связь математических методов с наукой и техникой через теорию графов;

- помочь учащимся отойти от математических штампов; расширить их математический и общенаучный кругозор.

- обеспечить формирование и развитие навыков самообразования через поисковую и исследовательскую работу;

- сформировать восприятие математики как единого языка познания;

- создать положительную мотивационную базу для самостоятельного изучения теории графов.

Учебно-тематический план

№ п/п	Тема занятия	Кол-во часов	Форма проведения занятия	Форма контроля.
1.	Сведения из истории графов. Граф и его элементы. Некоторые свойства и теоремы.	1	Лекция - беседа	Лабораторно-графическая работа
2.	Эйлеров и гамильтонов циклы. Задачи о мостах. Рисование фигур единым росчерком.	2	Лекция. Практическая работа.	Решение задач. Лабораторно-графическая работа. Самостоятельная работа. Конкурс красивых задач.
№ п/п	Тема занятия	Кол-во часов	Форма проведения занятия	Форма контроля.
3.	История лабиринтов. Геометрическая постановка задачи о лабиринте. Способы прохождения лабиринта. Лабиринты и графы.	2	Сообщения учащихся. Беседа. Выполнение практических работ.	Поисковые задания. Практическая работа.
4.	«Задача четырех красок». Графы и правильная раскраска карты.	2	Сообщение по теме. Практическая работа.	Творческие задания. Выполнение практических работ.
5.	Графы с цветными ребрами и их свойства.	1	Практикум по решению задач.	Сообщение по теме. Исследовательские задания.
6.	Дерево и лес. Понятие дерева в теории графов, применение деревьев в решении различных задач.	2	Лекция. Практикум по составлению дерева решений.	Творческие и исследовательские задания.
7.	Графы и логические задачи.	2	Практическое занятие.	Марафон задач. Зачетная работа. Выступления с рефератами.
8.	Сетевые графы. Элементы теории планирования и управления.	2	Лекция учителя. Комментированный разбор задачи.	Деловая игра.
9.	Применение теории графов в различных областях науки и техники.	1	Урок-конференция.	Защита исследовательских работ. Отбор работ на НПК.
10.	Зачетный урок.	1	Выполнение зачетной работы.	Итоговая работа. Выставка работ.

Содержание программы.

Программа курса состоит из 10 разделов и рассчитана на учащихся 9 классов. На изучение курса целесообразно отвести 16 часов.

Тема 1. Сведения из истории графов. Граф и его элементы.

В этой теме приводится характеристика «Геометрии положений» (топологии), данная Эйлером в связи с решением исторической задачи о кенигсбергских мостах; формулируются основные понятия теории графов.

Исследование задачи о мостах Кенигсберга Эйлер в 1736 г представил в Петербургскую Академию Наук. Работа начинается определением той области математики, к которой относятся подобные вопросы:

«Кроме той области геометрии, которая рассматривает величины, и способы измерения… Лейбниц первым упомянул о «геометрии положения», она занимается только расположением частей фигуры друг относительно друга, отвлекаясь от их размеров. Недавно мне пришлось слышать об одной задаче, относящейся к геометрии положения, и я решил изложить здесь в виде примера найденный мной способ решения этой задачи».

Далее Эйлер обосновывает невозможность решения этой задачи.

- Понятие графа и его элементов. Примеры графов. Полный граф. Четность вершины графа. Основные теоремы теории графов.

Если все вершины графа четные, граф можно начертить одним росчерком. Порядок движения любой.
Граф с двумя нечетными вершинами можно начертить одним росчерком, начиная движение с одной и заканчивая на другой нечетной вершине.
Граф с более чем двумя нечетными вершинами нельзя начертить одним росчерком.

рафами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых (примеры графов изображены на рисунке).

С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.

Познакомимся с основными понятиями теории графов при решении несложной задачи.

Задача: Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями. Сколько всего рукопожатий было сделано?
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени (рис.2), а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена (рис. 3).

Нулевой граф с пятью вершинами

Неполный граф с пятью вершинами

Точки А, Б, В, Г, Д называются вершинами графа, а отрезки линий, соединяющие эти точки — ребрами графа. При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; Длины отрезков и расположение точек произвольны.
Например, все три фигуры на рисунке изображают один и тот же граф.

Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.
1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рисунке 2. Такая схема, состоящая из «изолированных» вершин, называется нулевым графом.
2. Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рисунка З: пожали руки А и Б, А и Г, Д и Г, В и Д. Следующий момент, когда добавятся, например, пожатия рук А и В, Г и Б, попробуйте изобразить сами.
Графы, в которых не построены все возможные ребра , называются неполными графами.
3. На рисунке 4 изображен граф, соответствующий всем совершенным рукопожатиям. Этот граф является полным графом.

Полный граф с пятью вершинами

Если подсчитать число ребер графа, изображенного на рисунке 4, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.

Заметим, что если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2

Действительно, количество ребер в полном графе с n вершинами определяется как число неупорядоченных пар, составленных из всех n точек-ребер графа, т. е. как число сочетаний из n элементов по 2:
Граф, не являющийся полным, можно дополнить до полного с теми же вершинами, добавив недостающие ребра. Так, например, на рисунке 3 изображен неполный граф с пятью вершинами. На рисунке 4 ребра превращающие граф в полный граф изображены другим цветом, совокупность вершин графа с этими ребрами называется дополнением графа.

Тема 2. Эйлеров и Гамильтонов циклы. Задачи о мостах. Рисование фигур единым росчерком.

Учащимся дается понятие об эйлеровом и гамильтоновом циклах.

Цикл в графе, содержащий каждое ребро один раз, называется эйлеровым; цикл называется гамильтоновым, если он содержит каждую вершину один раз. Условие существования эйлерова цикла: граф должен быть связным, каждая его вершина должна иметь четную локальную степень.

Граф может быть и эйлеровым, и гамильтоновым, или одним из них, или ни тем ни другим.

К рассмотрению предлагаются различные задачи о мостах и их вариации, рассматриваются головоломки на рисование фигур единым росчерком; выполняются графические и творческие работы, самостоятельная работа.

Учащимся предлагается составление аналогичных задач с учетом свойств графов.

Рассматриваются задачи на «маршруты путешествий» и «осмотр достопримечательностей»

Рассматривается математическая постановка игры Гамильтона и ее близость к практическим задачам, например, об эффективном использовании подвижного состава или оборудования. Предполагается проведение конкурса на самую красивую графическую или текстовую задачу.

Тема 3. История лабиринтов.

Происхождение задач о лабиринтах относится к глубокой древности и теряется во мраке времен.

Слово «лабиринт» (греческое) означает «ходы в подземельях».

Решению задачи о лабиринтах предпосылаются исторические справки – чтобы показать интерес к этой задаче и дать наглядное представление о существовавших и существующих лабиринтах.

Возможен ли безвыходный лабиринт?

Задача о прохождении лабиринта приобретает практический интерес, поскольку устройство линий электропередач, канализации, сетей дорог, каналов и т.д. – все это более или менее сложные лабиринты.

Начало решению вопроса о существовании безвыходных лабиринтов положено Эйлером. Результаты его изысканий привели к заключению, что нет безвыходных лабиринтов.

Учащиеся знакомятся с геометрической постановкой задачи о лабиринтах; решают общую задачу, выполняют поисковые задания.

Нарисовав соответствующий лабиринту граф, используют способ обхода всех ребер для нахождения выхода.

Решение (т.е. маршрут, ведущий к цели) каждого лабиринта может быть найдено одним их трех сравнительно простых методов.

Первый метод – МЕТОД ПРОБ И ОШИБОК. Выбирайте любой путь, а если он заведет вас в тупик, то возвращайтесь назад и начинайте все сначала.
Второй метод – МЕТОД ЗАЧЕРКИВАНИЯ ТУПИКОВ. Начнем последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой. Незачеркнутая часть коридоров будет выходом или маршрутом от входа к выходу или к центру.
Третий метод – ПРАВИЛО ОДНОЙ РУКИ. Оно состоит в том, что по лабиринту надо двигаться, не отрывая одной руки (правой или левой) от стены.

Тема 4. Задача четырех красок.

Учащиеся знакомятся с задачей раскраски карты. Задача известна достаточно давно, но в качестве теоремы или задачи впервые была выдвинута Мебиусом в 1840 году. Суть задачи в следующем.

Для всякой карты достаточно четырех различных красок, чтобы любые две области, имеющие общую границу, не были окрашены одним цветом; причем все равно, сколько областей, как причудливы их очертания и как сложно их взаимное расположение.

Прослеживается аналогия этой задачи с Эйлеровой задачей о мостах, задачей о лабиринтах.

Учащимися формулируются условия возможности раскраски двумя красками, тремя, условия «правильной раскраски».

Учащиеся выполняют большое количество практических заданий, создают и раскрашивают собственные карты.

Тема тем более актуальна, что предположение о 4-х красках никто не доказал, но никто и не опроверг.

Впервые над этим вопросом задумались картографы в середине прошлого века. Не найдя ответа, они обратились к математикам. Доказано, что любую карту можно правильно раскрасить пятью красками, а так же показано, что существуют карты, которые нельзя правильно раскрасить в три цвета. Не доказано, что любую карту можно правильно раскрасить четырьмя красками, но не найдена ни одна карта, которую нельзя было бы раскрасить четырьмя красками.

Тема 5. Графы с цветными ребрами и их свойства.

Тема рассматривает графы, соответствующие таким ситуациям, при котором каждая пара каких-либо элементов множества находится между собой в каком-либо, но только одном отношении.

Например, среди участников чемпионата в какой-то момент есть и уже сыгравшие, и еще не сыгравшие друг с другом. Или: среди множества стран есть установившие и не установившие дипломатические отношения.

Для наглядности на рисунках ребра, соответствующие разным отношениям, окрашивают разным цветом. Свойства графов формулируются в ходе решения задач.

Тема 6. Понятие дерева в теории графов.

Знакомство учащихся с важным классом графов, называемых деревьями, предваряется упражнениями типа: «Нарисуйте граф с семью вершинами и шестью ребрами, не имеющий ни одного цикла».

Деревья определяются как графы, не имеющие циклов. Это одно из наиболее часто встречающихся в теории графов понятий, одновременно простое и удобное в обращении.

Вводятся понятия, связанные с деревьями, рассматриваются особенности деревьев и возможности их использования при решении самых разнородных задач – таких, как подсчет изомеров химического соединения, отыскание кратчайшего пути, комбинаторные задачи, вероятностные задачи, а также использование деревьев в генетике.

Кроме того, обобщается применение деревьев при описании различных вариантов игр и сочетаний или разбиений композиций.

Ребра графов, являющегося деревом, иногда называют ветвями дерева, а само дерево – деревом вариантов. Вычерчивать дерево полезно, когда требуется записать все существующие комбинации элементов.

Данная тема предполагает задания поискового и исследовательского характера.

Тема 7. Графы и логические задачи.

Обобщается возможность применения графов при решении некоторых типов логических задач; рассматриваются задачи на переливание, взвешивание, организацию круговых турниров и прочее. Проводится конкурс решения задач, выполняется текстовая работа.

Тема 8. Сетевые графы.

Данная тема показывает построение сети сложного комплекса работ, определение по сети самого ответственного участка; формирует навык определения времени завершения работ и поиска резервов времени.

Все вводимые в этой теме понятия имеют естественную природу; рассматривается комплекс работ, достаточно близкий и знакомый учащимся. Учащиеся знакомятся с основными правилами построения сетевых графиков, что помогает рациональному планированию. Тема допускает разделение расчетной и графической работ между группами учащихся.

Наиболее удачной формой занятия по данной теме можно считать деловую игру.

Тема 9. Применение теории графов в различных областях науки и техники.

Целью данного занятия является ознакомление учащихся с применением теории графов в различных областях науки и техники. Работа исследовательских и поисковых групп освещает вопросы использования графов в сетевом планировании, математической экономике, физике и электротехнике, биологии, химии, генетике и так далее.

Занятие проводится в виде пресс-конференции или круглого стола. Организуется стендовая защита поисковых и исследовательских работ.

Тема 10. Зачет.

На занятии подводятся итоги изучения курса, учащиеся выполняют итоговую зачетную работу.

Литература для учащихся.

Барр С. Россыпи головоломок.- М. «Мир». 1987.
Болл У, Коксетер Г. Математические эссе и развлечения. – М. «Мир», 1986.
Гарднер М. Математические головоломки и развлечения. – М. «Мир», 1971.
Гарднер М. Крестики-нолики. М., «Мир», 1988.
Графы // Квант. 1994. - №6.
Игнатьев Е.И. В царстве смекалки. Ростов-на-Дону, Ростовское книжное издательство, 1995.
Кордемский Б.А. Математические завлекали. – М.: Издательский дом Оникс: Альянс – В, 2000.
Перельман Я.И. Занимательные задачи и опыты. – М, «Детская литература», 1972.
Топология графов // Квант. – 2005. - №3.
Энциклопедия для детей. Том 11. Математика. Тема «Графы». – М.: Аванта, 1998.

Литература для учителя

Абрамов А.М, Березина Л.Ю. и др. Методика факультативных занятий в 7-8 классах. – М. «Просвещение», 1981.
Альхова З.Н., Макеева А.В Внеклассная работа по математике. – Саратов: «Лицей», 2002.
Асарина Е.Ю., Фрид М.Е. Математика выводит из лабиринта. – М. «Контекст», 1995.
Березина Л.Ю. Графы и их применение. – М. «Просвещение», 1979.
Гусев В.А, Орлов А.И. Розенталь А.Л. Внеклассная работа по математике в 6-8 классах. – М., «Просвещение», 1984.
Графы и кратчайшие расстояния в них. – Математика. Приложение к газете «1 сентября». – 2001 - №15, 16.
Литвинова С.А, Куликова Л.В, и др. За страницами учебника математики. Волгоград: Панорама, 2006.
Нестеренко Ю.В., Олехник С.Н., Потапов М.К. Задачи на смекалку. М, «Дрофа», 2005.
Смирнов Е.С. Курс наглядной геометрии. – М. «Просвещение», 2002.
Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. – М. «Дрофа», 2001.

Приложение 1

Тема 1

Нарисуйте полный граф с n вершинами, если:

n=2, n=3, n=5.

Скольким ребрам принадлежит вершина в полном графе с n вершинами,

n=3, n=5, n=k?

Существует ли полный граф с семью ребрами?
Сколько ребер в полном графе с n вершинами, если

n =3, n=4, n=5?

5. Найдется ли граф с пятью вершинами, степени которых все различны, т.е. равны 0, 1, 2, 3, 4?

6. Нарисуйте граф с 5 вершинами, две из которых имеют одинаковую степень.

7. Изобразите три разных графа, с пятью вершинами каждый, у которых нет ни одного цикла.

8. Лабораторно-графическая работа.

Тема 2

На рисунке схематически изображена речная сеть Москвы: река Москва, реки Яуза и Сходня, Химкинском водохранилище, острова. Через реки переброшены мосты, связывающие различные участки суши. Можно ли обойти за один раз все мосты на рисунке, проходя через каждый не более одного раза?

Контрабандист решил побывать во всех странах Европы, пересекая границу каждой только однажды. Возможно ли такое путешествие?

Попробуйте, не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии, вычертить следующие фигуры.

Тема 3.

Нарисуйте граф, соответствующий данному лабиринту.
Убедитесь в том, что, войдя в лабиринт, изображенный на рисунке, можно, касаясь правой рукой стены, дойти до центра и вернуться.
У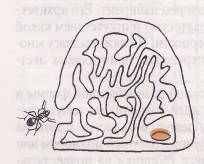бедитесь, что из любой точки лабиринта в его центр можно попасть, пользуясь правилом одной руки.
Как можно достать из муравейника зернышко.

Это лабиринт английского короля Вильгельма III, состоит из аллей и изгородей. Нужно пройти в центр к деревьям и скамейкам под ними.

Найдите путь к беседке, расположенной в парке.

Тема 4.

Раскрасьте предложенные карты минимально возможным количеством красок.
Придумайте необычную карту и раскрасьте ее в минимальное количество цветов.
Создайте карту, которую можно раскрасить в две, три, четыре краски.

Тема 5.

Шесть школьников участвуют в круговом шахматном турнире. Доказать, что среди них найдутся три участника, которые уже провели все встречи между собой или еще не сыграли друг с другом ни одной партии.
На карте выбраны пять городов. Среди них из любых трех найдутся два, соединенные авиалиниями, и два – несоединенные. Доказать: 1) Каждый город соединен авиалиниями непосредственно только с двумя другими. 2) Вылетев из любого города, можно облететь остальные, побывав в каждом по разу и вернуться назад.
Докажите, что если каждый из пяти человек переписывается только с двумя другими, то не найдется трех человек, которые все переписываются между собой.
Докажите, что не найдется девяти человек таких, чтобы каждый был знаком ровно с тремя другими.
Докажите, что среди шести углов (острых) найдутся три угла А, В, С такие, что все их парные суммы А+В, А+С, В+С одновременно либо больше 90 ⁰, либо одновременно не больше 90 ⁰.

Тема 6.

Нарисуйте граф с семью вершинами, в котором для любых двух вершин существует только один связывающий их путь.
Сколько различных трехзначных чисел можно записать с помощью цифр 0, 1, 2, если цифры в числе могут повторяться?
Составьте схему проведения розыгрыша кубка по олимпийской системе, в которой участвуют 19 команд.
Сколько различных способов обедов П.И.Чичиков мог насчитать из блюд, выставленных на столе у П.П.Петуха, если бы на каждый обед выбирать одно холодное блюдо, одно первое, одно второе, одно третье? На столе у П.П.Петуха на этот раз были выставлены студень с хреном, красная икра, свежепосоленная рыба; на первое – уха из стерляди, щи с грибами; на второе – осетрина жаренная, теленок жареный на вертеле; на третье – арбузы, груши.
Используя меню школьной столовой, укажите все возможные обеды из двух блюд, которые может заказать посетитель. Свой ответ проиллюстрируйте, построив дерево возможных вариантов.
Перечислите все возможные сочетания деловой одежды, если у вас в гардеробе брючный костюм черного цвета, белая и голубая блузки, синяя юбка и серый джемпер.
Составьте генеалогическое древо династии Романовых.
Постройте деревья, соответствующие гексану и изогексану. Определите количество различных изомеров у изогексана.
Изобразите дерево возможных исходов при троекратном бросании монеты.
Постройте дерево игры, показывающее ходы партнеров, приводящие к победе «крестиков», если игра начата ходами: а) (х1) и (о2), б) (х1) и (о9); в) (х5) и (о8).
Рассади участников «Большой восьмерки» за круглым столом всеми возможными способами.

Тема 7.

Беседуют трое друзей – Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас – блондин, другой – брюнет, третий – рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?
В Артеке за круглым столом оказалось пятеро ребят из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между Томичем и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидел пермяк и Алеша. Коля никогда не был в Санкт-Петербурге, Юра не бывал в Москве и Томске, а Томич с Толей регулярно переписываются. Определите, кто в каком городе живет.

3. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что:

Вода и молоко не в бутылке.
Сосуд с лимонадом стоит между кувшином и сосудом с квасом.
В банке не лимонад и не вода.
Стакан стоит между банкой и сосудом с молоком.

В каком сосуде находится, какая из жидкостей?

4. Три подруги вышли в белом, зеленом и синем платьях и туфлях. Известно, что только у Ани цвета платья и туфель совпадали. Ни туфли ни платье Вали не были белыми. Наташа была в зеленых туфлях.

5. На улице, встав в кружок, беседуют Аня, Валя, Галя и Надя.

Девочка в зеленом платье – не Аня и не Валя – стоит между девочкой в голубом платье и Надей.
Девочка в белом платье стоит между девочкой в розовом и Валей. Какого цвета платье у каждой из девочек?

В семье четверо детей. Им 5, 8, 13 и 15 лет. Зовут их Аня, Боря, Вера и Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори, а сумма лет Ани и Веры делится на три?
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7-и 11-литровых сосудов и крана с водой отмерить 2 литра?
Сколько существует различных трехзначных чисел, в записи которых участвуют лишь цифры 1, 2, 3 и 4?
Среди чисел, о которых говорится в задаче 8, сколько существует таких, в записи которых цифры не повторяются?

Тема 8.

В школе готовится новогодний вечер.

А) Назовите отдельные работы, которые при этом должны быть выполнены.

Б) Назовите несколько событий, которые включены в соответствующий сетевой график.

2. Приведите пример комплекса работ, который можно представить сетевым графиком. Составьте такой график.

3. По заданному сетевому графику определите критический путь и ранний из возможных сроков наступления завершающего события.

4. По сетевому графику определите поздний срок наступления каждого события и резерв времени.

Тема 9.

Примерные темы поисковых и исследовательских заданий, рефератов и докладов учащихся приведены в Приложении 4.

Тема 10.

Примерное содержание зачетной работы.

Нарисуйте полный граф с 6 вершинами.
Определите степень какой-нибудь вершины полного графа с 20 вершинами.
Определите количество ребер у полного графа с 20 вершинами.
Нарисуйте граф с 6 вершинами, имеющий два цикла, каждый из которых проходит через все вершины.
Изобразите три различных графа с шестью вершинами, не содержащих циклов.
Приведите примеры связных и несвязных графов с 6 вершинами.
Нарисуйте два связных графа с 5 вершинам так, чтобы один из них являлся деревом.
В мастерской имеется 10 различных станков. Известно, что каждый из 10 рабочих этой мастерской умеет работать только на двух станках и на каждом станке умеют работать только двое рабочих. Можно ли расставить рабочих у станков так, чтобы каждый стоял у станка, на котором умеет работать?
Придумайте жизненную ситуацию, описываемую ориентированным графом с 5 вершинами.

Назовите работы и события, которые можно выделить при проведении игры баскетбольных команд двух школ.

Приложение 2.

В качестве поисковых и исследовательских заданий, тем для рефератов и докладов учащимся могут быть предложены следующие примерные темы:

1. Графы в головоломках.

2. Графы и игры на шахматной доске.

3. Геометрическая задача о лабиринтах.

4. Использование графов в школьных учебниках.

5. Графы в решении логических задач.

6. Графы и подсчет числа изомеров.

7. Графы в генетике.

8. Расчет сетевых графиков.

9. Графы и транспортные сети.

10. Графы в электротехнике.

11. Графы в психологии.

12. Проблема четырех красок.

13. Графы и поиски анаграмм.

14. Графы в физике.

15. Графы с цветными ребрами.

Blog

Липецка Учитель Тарасова Светлана Васильевна. Предмет математика. Класс 9 элективный курс

Содержание