Математика экономического профиля
| Вид материала | Документы |
- Содержание, 90.14kb.
- Э. Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля:, 101.76kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Рабочая программа дисциплины «актуарная математика», 161.92kb.
- Расшифровка : Математика, 146.94kb.
- Примерная программа наименование дисциплины мелиорация рекомендуется для направления, 291.84kb.
- Серия Современное образованием, 8060.72kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
Цель освоения дисциплины – обучить студентов применению методов математического анализа для исследования геометрических свойств фигур на плоскости и в пространстве, а также приложению этих методов для решения прикладных задач. Дисциплина должна содействовать фундаментализации образования и развитию математического мышления. Курс призван расширить кругозор и развить математическую культуру, включающую в себя четкое представление о роли геометрии в современной математике, ее связи с другими математическими дисциплинами.
Задачи, соответствующие цели освоения дисциплины: формирование у студентов: представлений о дифференциальной геометрии, как одной из важнейших математических дисциплин, имеющей свой предмет, задачи и методы; знаний и умений, необходимых для освоения и использования методов дифференциальной геометрии при решении теоретических и прикладных задач, для дальнейшего самообразования в области современной математики.
Краткое содержание дисциплины
Определение векторной функции одного и нескольких скалярных аргументов. Годограф. Предел векторной функции. Непрерывность и дифференцируемость. Разложение векторной функции в ряд Тейлора.
Понятие кривой. Способы задания кривой. Плоские и пространственные кривые. Касательная прямая. Естественный параметр. Трехгранник Френе. Кривизна плоских кривых. Кривизна и кручение пространственных кривых. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента.
Определение поверхности. Способы задания поверхностей. Кривые на поверхности. Координатные линии. Касательная плоскость. Первая квадратичная форма поверхности. Длина дуги кривой на поверхности. Угол между кривыми на поверхности. Площадь области на поверхности. Вторая квадратичная форма поверхности. Инварианты пары квадратичных форм. Кривизна кривой на поверхности. Соприкасающийся параболоид поверхности. Главные направления и главные нормальные кривизны. Тип точки на поверхности. Теорема Эйлера. Экстремальные свойства главных направлений. Отыскание главных направлений и главных нормальных кривизн. Гауссова и средняя кривизна поверхности. Деривационные формулы. Символы Кристоффеля.
Изометричные поверхности. Понятие о внутренней геометрии поверхностей. Геодезическая кривизна кривой на поверхности. Геодезические линии. Полугеодезическая система координат. Теорема Гаусса-Бонне.
Многомерные геометрические объекты: проективное пространство, аффинная карта проективного пространства, модели проективных пространств малой размерности, метрические группы.
Дисциплина «Топология»
Цель освоения дисциплины. Роль топологии в системе университетского образования весьма значительна. Без привлечения топологических методов и понятий вряд ли возможно построить курсы математического анализа, дифференциальных уравнений, дифференциальной геометрии, механики, функционального анализа, отвечающие современного состоянию этих математических дисциплин.
В курсе данной дисциплины студенты знакомятся с основами топологии и её приложениями. В результате освоения курса студенты должны свободно ориентироваться в основных разделах дисциплины, что включает: теории кривых на плоскости и в пространстве, поверхности, топологические и метрические пространства, гладкие многообразия, Риманову метрику, тензорных анализ, гомотопию, степень отображения
Краткое содержание дисциплины
Г
ладкие многообразия. Общие сведения из общей топологии6 топологическое пространство, метрическое пространство, непрерывное отображение, гомеоморфизмы, компактность, связность; определение гладкого многообразия, отображение многообразий: гладкие поверхности, матричные группы, проективное пространство; многообразие с краем; риманова метрика; касательный вектор, касательное пространство к многообразию, векторные поля на многообразии.
Тензорный анализ на многообразиях. Тензоры на римановом многообразии: общее определение тензора, алгебраические операции над тензорами, поднятие и отпускание индексов, оператор Ходиса; кососимметрические тензоры, дифференциальные формы, внешнее произведение дифференциальных форм, внешняя алгебра; поведение тензоров при отображениях, дифференциал отображения, отображения касательных пространств.
Связность и ковариантное дифференцирование: ковариантная производная тензора, параллельный перенос векторных полей, геодезические связности, согласование с метрикой; тензор кривизны, порожденный метрикой; тензоры кривизны двух- и трехмерных многообразий.
Дифференциальные формы и теория интегрирования: разбиение единицы на многообразия, интеграл дифференциальной формы, примеры; криволинейные и поверхностные интегралы второго рода; общая формула Стокса; примеры: формулы Грина, Стокса и Остроградского Гаусса.
Элементы топологии многообразий. Гомотопия: определение гомотопий, аппроксимация отображений и гомотопий, относительная гомотопия; степень отображения: определение степени, гомотопическая классификация многообразий в сферу; степень и интеграл; степень векторного поля на поверхности; теорема Гаусса-Боне; индекс особой точки векторного поля; теорема Пуанкаре – Бендиксона.
Дисциплина «Функциональный анализ и интегральные уравнения»
Цель освоения дисциплины. В результате изучения курса студент должен знать основные определения и теоремы курса, уметь решать типичные задачи, такие как нахождение нормы линейного оператора, вычисление спектра линейного оператора, решение интегральных уравнений, вычисление сопряженных операторов; иметь представление о месте и роли функционального анализа в современной математике, о теории и методах обобщенных функций, о нелинейном анализе.
Краткое содержание дисциплины
В
ведение: возникновение функционального анализа как самостоятельного раздела математики; современное развитие функционального анализа и его связь с другими областями математики. Метрические и топологические пространства: множества, алгебра множеств; счетные множества и мощности континуума; метрические пространства открытые и замкнутые множества; компактные множества в метрических пространствах; критерий Хаусдорфа; полнота и пополнение; теорема о вложенных шарах; принцип сжимающих отображений; топологические пространства. Мера Лебега: Построение меры Лебега на прямой; общее понятие σ-аддитивной меры; лебеговское продолжение меры. Измеримые функции: Измеримые функции и их свойства. Интеграл Лебега: Определение интеграла Лебега; класс суммируемых функций; предельный переход под знаком интеграла; связь интеграла Лебега с интегралом Римана. Прямое произведение мер и теорема Фубини; пространства ; неравенства Гельдера и Минковского. Интеграл Стилтьеса: Интеграл Римана-Стилтьеса Лебега-Стилтьеса. Теорема Радона-Никодима. Нормированные пространства: Определение линейного нормированного пространства; примеры норм; банаховы пространства; примеры нормированных пространств. Гильбертовы пространства: скалярное произведение; неравенство Коши-Буняковского-Шварца; ортогональные системы; неравенство Бесселя; базисы и гильбертова размерность; теорема об изоморфизме; ортогональное дополнение. Линейные операторы в нормированных пространствах: Линейные операторы и функционалы в нормированных пространствах. Норма оператора. Принцип равномерной ограниченности. Разные виды сходимости в пространстве линейных ограниченных операторов. Сопряженные пространства оператора: Сопряженное пространство, его полнота; теорема Хана-Банаха о продолжении линейного функционала; общий вид линейных функционалов в некоторых банаховых прстранствах4 Сопряженные и самосопряженные операторы в гильбертовых пространствах. Обратные операторы: Обратные и односторонне обратные операторы. Теоремы Неймана и Банаха об обратном операторе; Спектр и резольвента. Компактные операторы: Теория Рисса – Шаудера уравнений с компактными операторами. Альтернатива Фредгольма. Спектр компактного оператора. Интегральные уравнения: Компактность интегральных операторов. Понятие об индексе; теорема Фредгольма; Методы решения уравнений Фредгольма и Вольтерра второго рода. Примеры использования теоремы Фредгольма (задача Штурма – Лиувилля, теория потенциала, индекс дифференциального оператора). Линейные операторы в гильбертовых пространствах: Самосопряженные (эрмитовы) и унитарные операторы; ортопроекторы; спектр эрмитова и унитарного оператора; теорема Гильберта о компактных эрмитовых операторах; функциональное исчисление; приведение оператора к виду умножения на функцию; спектральная теорема; неограниченные самосопряженные операторы; примеры. Линейные топологические пространства: Линейные топологические пространства; функционал Минковского;нормируемость и метризуемость; топологии в сопряженном пространстве; слабая компактность шара в сопряженном пространстве. Обобщенные функции: Основные пространства гладких функций; пространства обобщенных функций; операции над обобщенными функциями; умножение на гладкую функцию, дифференцирование, замена переменных, преобразование Фурье. Элементы нелинейного анализа: Дифференцируемость по Гато и по Фреше. Экстремум функционала; классические задачи вариационного исчисления; уравнение Эйлера, вторая вариация; условия Лежандра и Якоби.
Дисциплина «Теория функций комплексного переменного»
Цель освоения дисциплины – расширение математического мировоззрения, формирование основ пространственного мышления, развитие аналитических способностей, выработка практических навыков применения математического аппарата ТФКП при решении прикладных задач гидромеханики, электродинамики, геофизики; закрепление знаний и навыков интегрирования.
В результате изучения дисциплины студенты должны иметь представление об основных методах теории функций комплексного переменного, применяемых в научно-исследовательской работе и практической деятельности; знать основные понятия и теоремы в области теории функций комплексного переменного; уметь оперировать с комплексными числами во всех формах; дифференцировать, интегрировать и находить разложения в ряды Тейлора и Лорана функций комплексного переменного; исследовать аналитические свойства функций, находить нули и особые точки функций; применять теорию вычетов для вычисления контурных, определенных и несобственных интегралов; строить конформные отображения односвязных областей.
Краткое содержание дисциплины
Комплексные числа: комплексные числа, комплексная плоскость; модули и аргументы комплексного числа; числовые последовательности и их пределы, ряды; стереографическая проекция, её свойства; сфера Римана, расширенная комплексная плоскость, множества на плоскости, области и кривые.
Функции комплексного переменного и отображения множеств: функции комплексного переменного; предел функции; непрерывность, модуль непрерывности; дифференцируемость по комплексному переменному, условие Коши-Римана; аналитическая функция; геометрический смысл аргумента и модуля производной; понятие о конформном отображении. Элементарные функции: целая линейная и дробно - линейная функция, их свойства, общий вид дробно - линейного отображения; экспонента и логарифм, степень с произвольным показателем; понятие о Римановой поверхности на примерах логарифмической и общей степенной функции; функция Жуковского; тригонометрические и гиперболические функции. Интеграл по комплексному переменному и его свойства; связь с криволинейными интегралами 1 - го и 2- го рода; сведение к интегралу по действительному переменному; первообразная функции, формула Ньютона- Лейбница; переход к пределу под знаком интеграла;
Интеграл Коши; интегральная формула Коши; бесконечная дифференцируемость аналитических функций, формула Коши для производных; теорема Морера.
Последовательность и ряды аналитической функции в плоскости: теорема Вейерштрасса; степенные ряды; теорема Абеля, формула Коши - Адамара; разложение аналитической функции в степенной ряд, единственность разложения; неравенство Коши для коэффициентов степенного ряда; действия со степенными рядами.
Теорема единственности и принцип максимума модуля: нули аналитической функции, порядок нуля; теорема единственности для аналитических функций; принцип максимума модуля.
Ряд Лорана: ряд Лорана, область его сходимости; разложение аналитической функции в ряд Лорана, единственность разложения, формулы и неравенства Коши для коэффициентов; теорема Лиувилля и теорема об устранимой особой точке.
И
золированные особые точки однозначного характера; классификация изолированных особых точек однозначного характера по поведению функции и ряду Лорана; полюс, порядок полюса; существенная особая точка, теорема Сохоцкого-Вейерштрасса, понятие о теореме Пикара; бесконечно удаленная точка как особая.
Вычеты, принцип аргумента: определения вычета, теорема Коши о вычетах, вычисления вычетов; применение вычетов; логарифмический вычет, принцип аргумента; теорема Руше и теорема Гурвица.
Отображения посредством аналитических функций: принцип открытости и принцип области; теорема о локальном обращении; однолистные функции, критерий локальности однолистности и критерий конформности в точке, достаточное условие однолистности (обратный принцип соответствия границ); дробно - линейность однолистнных конформных отображений круговых областей друг на друга; теорема Римана и понятие о соответствии границ при конформном отображении.
Аналитическое продолжение: аналитическое продолжение по цепи и по кривой; полная аналитическая функция в смысле Вейерштрасса, её риманова поверхность и особые точки; аналитическое продолжение через границу области, принцип симметрии.
Целые и мероморфные функции: целые функции, произведение Вейерштрасса; мероморфные функции; функции, мероморфные в расширенной плоскости.
Гармонические функции на плоскости: гармонические функции, их связь с аналитическими функциями; бесконечная дифференцируемость гармонических функций; теорема о среднем, теорема единственности и принцип максимума - минимума; инвариантность гармоничности при голоморфной замене переменных; теорема Лиувилля и теорема Гарнака об устранимой особой точке; интегралы Пуассона и Шварца; разложение гармоничных функций в ряды, связь с тригонометрическими рядами;
Прикладные задачи: задача Дирихле: применение конформных отображений для ее решения; гидромеханическое истолкование гармонических и аналитических функций.
Дисциплина «Уравнения с частными производными»
Цель освоения дисциплины: формирование основных понятий и методов теории уравнений математической физики для решения задач в рамках профессиональной деятельности.
Задачи, соответствующие цели:
- исследование гиперболических систем уравнений с частными производными первого порядка,
- классификация дифференциальных уравнений в частных производных второго порядка,
- изучение метода Фурье для уравнений математической физики,
- постановка начально-краевых задач для параболических и гиперболических уравнений,
- исследование эллиптических уравнений.
Краткое содержание дисциплины
Классификация линейных уравнений в частных производных второго порядка, приведение к канонической форме, постановка основных краевых задач для дифференциальных уравнений в частных производных второго порядка. В качестве примеров рассматривается вывод уравнений малых поперечных колебаний струны, малых поперечных колебаний мембраны, уравнения теплопроводности, уравнения гидродинамики, уравнение Лапласа, уравнение Пуассона, уравнение диффузии частиц, уравнения Навье-Стокса, бигармоническое уравнение, пример Адамара.
Теорема единственности и методы построения решений краевых задач для уравнений гиперболического типа, задачу Коши для одномерного однородного волнового уравнения, формулу Даламбера, метод разделения переменных (метод Фурье) построения решений краевых задач для уравнений гиперболического типа, задачу Штурма-Лиувилля, теорему Стеклова о разложимости.
Метод функций Грина решения краевых задач для уравнений параболического типа, построение функции Грина задачи Коши для уравнения теплопроводности, физическая интерпретация функции Грина, функция Грина для задачи распространения тепла в двухмерном и трехмерном пространствах. В качестве примеров рассматривается построение обобщенной δ-функции. В четвертом разделе рассматриваются теоремы единственности и методы построения решений краевых задач для уравнений эллиптического типа, сингулярные (фундаментальные) решения уравнения Лапласа, метод Фурье решения краевых задач для уравнений эллиптического типа, решение методом Фурье краевых задач для уравнений Лапласа и Пуассона в канонических областях. В качестве примеров рассматриваются гармонические функции, цилиндрические функции, сферические функции.
Дисциплина «Теория вероятностей»
Цель освоения дисциплины – знакомство студентов с основными понятиями, методами и результатами теории вероятностей.
Задачи, соответствующие цели освоения дисциплины:
- получение базовых знаний в области теории вероятностей,
- изучение свойств распределений случайных величин, предельных теорем, элементов теории случайных процессов,
- ознакомление с основами математического аппарата, необходимого для решения теоретических и практических задач;
- развитие логического мышления;
- привитие умения самостоятельно изучать научную литературу по математике и ее приложениям;
- повышение общего уровня математической культуры;
- выработка навыков математического исследования прикладных вопросов.
Краткое содержание дисциплины
Аксиоматика теории вероятностей. Случайные величины, их распределения и числовые характеристики. Основные предельные теоремы теории вероятностей. Однородные цепи Маркова. Основные понятия теории случайных процессов. Пуассоновский процесс. Винеровский процесс.
Дисциплина «Математическая статистика»
Цель освоения дисциплины – знакомство студентов с основными понятиями, методами и результатами математической статистики.
Задачи, соответствующие цели освоения дисциплины:
- получение базовых знаний в области теории математической статистики,
- изучение основных задач математической статистики: точечное и интервальное оценивание, проверка гипотез, исследование зависимостей,
- изучение вопросов построения математических моделей случайных экспериментов и выработке навыков применения изученных методов при решении практических задач.
Краткое содержание дисциплины
Статистические модели и основные задачи математического анализа, примеры; экспоненциальные семейства; статистическое оценивание, методы оценивания; достаточные статистики; линейная регрессия с гауссовыми ошибками; факторные модели; общие линейные модели; проверка линейных гипотез в линейных моделях; критерий Пирсона «хи-квадрат»; оценки наибольшего правдоподобия, состоятельность; понятие асимптотической нормальности случайной последовательности; асимптотическая нормальность оценок максимального правдоподобия.
Дисциплина «Теория случайных процессов»
Цель освоения дисциплины - формирование прочных знаний по основным понятиям стохастических процессов, выработка практических навыков построения и анализа случайных функций.
Краткое содержание дисциплины
Случайный процесс и его характеристики. Понятие о случайном процессе и его характеристиках. Эргодическое свойство стационарных случайных функций. Случайный процесс со счетным множеством состояний.
Элементы теории функций случайных аргументов. Понятие функции случайных аргументов. Среднее от функции по ансамблю аргументов. Среднее и дисперсия линейной функции случайных аргументов. Распределение функции случайных аргументов. Основные понятия случайных процессов в широком смысле. Гауссовы случайные функции. Метод Фурье для уравнений гиперболического и параболического типа. Пуассоновский процесс. Винеровский процесс. Ветвящийся процесс. Марковский случайный процесс. Применение Марковских случайных процессов.
Д
Непрерывные Марковские цепи. Свойства непрерывных Марковских цепей. Вывод уравнений А. Н. Колмогорова. Применение теории непрерывных Марковских цепей к процессам гибели и размножения. Примеры и практические задания.
Элементы теории массового обслуживания (ТМО). Введение в теорию массового обслуживания. Поток событий. Статистические испытания и проверка гипотез. Использование теории массового обслуживания в реальных СМО.
Дисциплина «Вариационное исчисление и методы оптимизации»
Цель освоения дисциплины – формирование основ классического вариационного исчисления и элементов теории оптимального управления, имеющих фундаментальное теоретическое значение, используемых в качестве математических моделей в естествознании и технике с помощью современных аналитических средств.
Задачи, соответствующие цели освоения дисциплины:
- формировать у студентов прочные знания по основам теории вариационного исчисления и методов оптимизации;
- выработать у студентов практические навыки составления математических моделей прикладных задач, выбора стратегии поиска и алгоритма решения;
- привить студентам умение самостоятельно изучать учебную и научную литературу в области вариационного исчисления и методов оптимизации;
- воспитать у студентов культуру мышления;
- развить математическую культуру и интуицию.
Краткое содержание дисциплины
Конечномерные экстремальные задачи и численные методы их решения. Конечномерная экстремальная задача. Правило множителей Лагранжа для задачи с ограничениями типа равенств. Элементы выпуклого анализа. Задача выпуклого программирования и теорема Куна-Таккера. Основные сведения о численных методах оптимизации. Численные методы решения задач безусловной минимизации. Методы условной минимизации.
Линейное программирование. Задача линейного программирования. Основы теории двойственности. Теоретические основы симплекс-метода.
Вариационное исчисление. Классическая задача вариационного исчисления. Задача Больца. Изопериметрическая задача. Сильный локальный минимум в классической задаче вариационного исчисления. Вторая вариация функционала. Достаточные условия минимума в классической задаче вариационного исчисления. Прямые методы вариационного исчисления.
Оптимальное управление. Задача оптимального управления. Связь между принципом максимума и классическим вариационным исчислением. Примеры решения задач оптимального управления. Теорема существования решения в одной задаче оптимального управления. Моделирование: процесса распространения заболевания, модель соревнования по бегу. Задача оптимального управления с фазовыми и смешанными ограничениями.
Достаточные условия оптимальности. Постановка задачи. Поле оптимального процесса. Двойственность и достаточные условия оптимальности. Задача оптимального управления, линейная относительно фазовых координат. Синтез оптимального управления. Двойственный метод в многомерных задачах оптимального управления. Решение задач оптимального управления двойственным методом.
Численные методы решения задач оптимального управления. Численное решение задач оптимального управления. Метод пристрелки для решения разрывных краевых задач для систем обыкновенных дифференциальных уравнений.
Достаточные условия оптимальности в дискретных задачах оптимального управления. Дискретный управляемый процесс. Эквивалентное представление минимизирующего функционала. Достаточные условия оптимальности в форме Кротова. Принцип Беллмана в дискретной задаче оптимального управления. Решение задач с использованием достаточных условий оптимальности.
Моделирование искусственной нейронной сети. Математическая модель искусственной нейронной сети. Дискретная задача оптимального управления. Оптимизация динамики нейронной сети.
Дисциплина «Методы вычислений»
Цель освоения дисциплины – подготовка к разработке и применению с помощью ЭВМ вычислительных алгоритмов решения математических задач, возникающих в процессе познания и использования в практической деятельности законов реального мира, посредством математического моделирования.
Задачи, соответствующие цели освоения дисциплины:
- изучение численных методов решения широкого круга математических задач;
- овладение способами численного решения математических задач с использованием современных программных пакетов и языков программирования;
- развитие логического и алгоритмического мышления.
Краткое содержание дисциплины
Теория погрешности. Понятие погрешности. Абсолютная и относительная погрешности. Округление чисел. Вычисление погрешности арифметических действий. Погрешность значений функции.
Теория матриц. Вычисление определителей. Вычисление обратной матрицы. LU – разложение матриц. Методы решения задач на собственные значения и собственные вектора.
Приближенные методы решения трансцендентных алгебраических уравнений. Постановка задачи численного решения уравнений. Методы отделения корней уравнения. Метод половинного деления (дихотомии). Метод итераций или метод последовательных приближений. Методы Ньютона. Метод касательных. Метод хорд.
Численные методы решения систем линейных алгебраических уравнений. Постановка задачи. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса. Метод Гаусса с выбором главного элемента. Метод Халецкого. Метод квадратных корней. Метод прогонки. Итерационные методы решения систем линейных алгебраических уравнений. Плохо обусловленные системы линейных алгебраических уравнений. Метод простой итерации. Метод Зейделя.
Численные методы решения систем нелинейных алгебраических уравнений. Постановка задачи. Матрица Якоби. Метод итераций. Метод Ньютона.
Численное интегрирование. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона-Котеса (прямоугольников, трапеций, Симпсона). Квадратурные формулы Гаусса. Метод Монте-Карло.
Методы интерполирования. Постановка задачи аппроксимации функций. Интерполяционный многочлен Лагранжа. Интерполяционный многочлен Ньютона. Интерполяция сплайнами. Погрешность многочленной интерполяции. Применение аппарата интерполирования. Обратная интерполяция. Рациональная интерполяция.
Статистическая обработка данных. Постановка задачи. Метод наименьших квадратов. Нахождение приближающей функции в виде линейной функции и квадратного трехчлена. Нахождение приближающей функции в виде других элементарных функций.
Численное дифференцирование. Постановка задачи численного дифференцирования. Численное дифференцирование на основе интерполяционной формулы Лагранжа. Численное дифференцирование на основе интерполяционной формулы Ньютона. Разностные аппроксимации производных. Метод неопределенных коэффициентов. О вычислительной погрешности формул численного дифференцирования.
Численные методы решения обыкновенных дифференциальных уравнений и их систем. Понятие о численном решении задачи Коши. Метод Эйлера. Методы Рунге-Кутта. Численное решение дифференциальных уравнений высших порядков. Численное решение систем дифференциальных уравнений первого порядка.
Численные методы решения дифференциальных уравнений в частных производных. Постановка задачи численного решения уравнений в частных производных. Метод сеток или метод конечных разностей. Приближенное решение дифференциальных уравнений в частных производных параболического типа. Приближенное решение дифференциальных уравнений в частных производных эллиптического типа. Приближенное решение дифференциальных уравнений в частных производных гиперболического типа.
Дисциплина «Теория чисел»
Цель освоения дисциплины – формирование прочных знаний по основам делимости целых чисел, сравнению первообразных корней и индексов; выработка практических навыков определения числовых функций, решения сравнений любой степени, перехода от действительного числа к цепным дробям и обратно, решения сравнений с помощью таблиц индексов и антииндексов; воспитание культуры мышления; развитие математической культуры и интуиции.
Задачи, соответствующие цели освоения дисциплины:
- студент обязан знать: свойства делимости целых чисел; определение второго числа; основную теорему арифметики; определение НОД, НОК чисел, определение функций
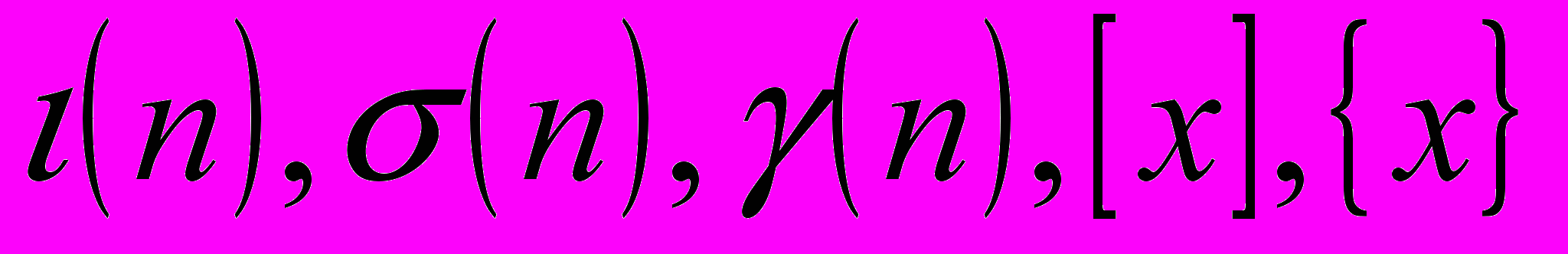; свойства мультипликативных функций; оценки Чебышева для функции П(x), определения конечной и бесконечной цепных дробей; теоремы о существовании цепных дробей; определения и формулы подходящих дробей, определение числового сравнения и сравнения с неизвестными; понятие полной и приведенной системы вычетов, понятие квадратичного вычета и невычета; свойства символа Лежандра, теорему о существовании первообразного корня по простому модулю; теорему об отыскании первообразных корней; понятие индекса, признаки делимости чисел; определение алгебраических и трансцендентных чисел; теорему Лиувилля;- студент должен уметь: записывать каноническое разложение составного числа; определять число простых чисел меньше заданного числа; определить НОД чисел с помощью алгоритма Евклида, находить целую и дробную части действительного числа; вычислять функции
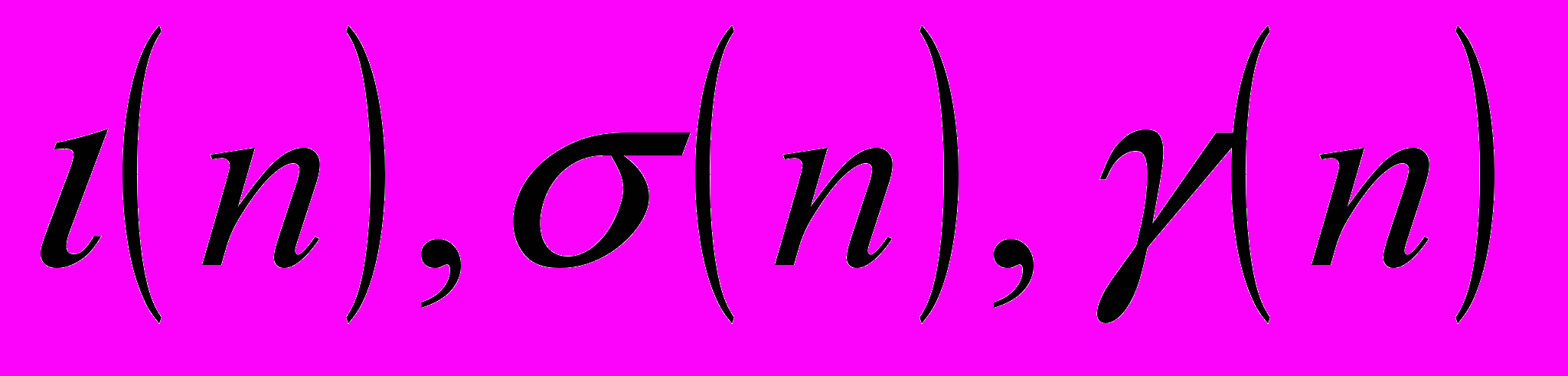по формулам, переходить из обычной записи действительного числа к цепной дроби обратно; находить подходящие дроби; решать линейное уравнение с двумя неизвестными в целых числах с помощью цепных дробей, применять свойства сравнений для их решения; находить полную и приведенную системы вычетов; применять теоремы Эйлера и Ферма при решении сравнений, сводить сравнения II степени к двучленным сравнениям; решать сравнения II степени по составному модулю, составлять таблицы индексов; решать двучленные сравнения с помощью вычетов; решать показательные сравнения, отыскивать остатки от деления некоторого числа на заданное; устанавливать признаки делимости чисел; определять, является ли число трансцендентным, алгебраическим;- студент должен иметь представление: о простых числах, арифметических функциях, цепных дробях, числовых сравнениях, квадратичных вычетах и невычетах, законе взаимности квадратичных вычетов, первообразных корнях и индексах, алгебраических и трансцендентных числах.
Краткое содержание дисциплины
Свойства делимости целых чисел. Простые числа. Решето Эратосфена. Теорема Евклида о бесконечности множества простых чисел. Основная теорема арифметики о разложении целых чисел не простые сомножители. НОД, НОК.
Целая и дробная части числа х. Разложение числа n на простые множители. Суммы, распространенные на делители числа. Мультипликативные функции. Функция Эйлера и ее свойства. Сумма делителей и число делителей. Оценки Чебышева для функции П(х) – числа простых чисел, не превосходящих х.
Конечные цепные дроби. Подходящие дроби и их свойства. Нахождение НОД двух чисел с помощью цепных дробей. Бесконечные цепные дроби. Разложение действительных чисел в цепные дроби. Приближение действительных чисел рациональными числами. Подходящие дроби как наилучшие приближения. Признак иррациональности числа. Иррациональность числа е.
Сравнения и их основные свойства. Вычеты и классы вычетов по модулю m. Кольца классов вычетов. Полная система вычетов. Приведенная система вычетов. Теорема Эйлера и Ферма. Сравнения n-ой степени по простому модулю. Теорема о равносильности сравнений. Теорема о числе решений сравнения. Теорема Вильсона. Сравнения n-ой степени по составному модулю. Сведения сравнения по составному модулю к системе сравнений по простому модулю.
С
Показатель числа по модулю m. Свойства показателей. Теорема о существовании первообразного корня по простому модулю. Первообразные корни по модулям р и 2р. Теорема об отыскании первообразных корней. Индексы по модулям р и 2р. Таблицы индексов. Двучленные сравнения n-ой степени. Существование решений. Степенные вычеты и невычеты n-ой степени. Число степенных вычетов. Критерий для отыскания степенных вычетов. Решение двучленных сравнений с помощью вычетов. Решение показательных сравнений. Число классовых первообразных корней.
Отыскание остатков от деления некоторого числа на заданное число. Установление признаков делимости чисел. Алгебраические и трансцендентные числа. Теорема Лиувилля о приближении алгебраических чисел рациональными числами. Существование трансцендентных чисел.
Дисциплины специализации
Дисциплина «Современные методы научных исследований в экономике»
Цель освоения дисциплины – формирование в теоретико-прикладном аспекте представлений о социальных процессах, явлениях и отношениях, происходящих в экономике; понимания социальных механизмов и резервов развития экономики; формирование гуманитарного видения роли экономики в жизни общества.
Задачи, соответствующие цели освоения дисциплины:
- осознание исторического места экономической социологии в системе научного знания, особенности ее предмета, методологии и метода в анализе процессов, связанных с экономической деятельностью,
- формирование представления о возможностях социологического анализа социально-эко-номических процессов, использования социологической информации в управлении экономикой;
- установление взаимосвязи и взаимодействия экономической и социальной сфер общества, особенностей его социально-экономической стратификации;
- установление влияния экономической культуры на экономическое поведение, формирование нового экономического мышления, повышение роли человеческого фактора в развитии экономики;
- раскрытие социальной природы труда, структуры социально-трудовых отношений, социальных механизмов формирования высокомотивированного трудового поведения;
- анализ социальных факторов развития трудовых ресурсов, проблем эффективной занятости населения, социальных последствий безработицы;
- выявление значений социальных критериев экономического прогресса, развития социально-ориентированной экономики, социальной защищенности отдельных групп населения.
Краткое содержание дисциплины
Экономическая социология как наука. Этапы становления и развития экономической социологии. Объект, предмет и задачи экономической социологии.
Социальные основы экономического поведения. Экономическое поведение и экономическое сознание. Экономическая культура как регулятор экономического поведения. Структура механизма мотивации экономического поведения. Социально-экономическая стратификация и развитие экономики.
Труд как социально-экономический процесс. Социальная сущность труда. Трудовая адаптация и социальный контроль в сфере труда. Социальное партнерство в сфере труда.
Социальные аспекты использования трудовых ресурсов. Трудовые ресурсы и отношения занятости. Безработица, ее структура и социальные последствия. Социальная роль предпринимательства.
Социальные механизмы управления экономическими процессами. Социальная политика занятости населения. Экономическая система как социальный институт. Качество жизни и социально-экономический прогресс.
Дисциплина «Теория игр и исследование операций»
Задачи, соответствующие цели: получение знаний и навыков по составлению математических моделей операций; знаний теоретических положений по основным типам задач исследования операций и основным типам игр; навыков по разработке алгоритмов решения задач исследования операций и теории игр в различных условиях информированности о неконтролируемых факторах.
Краткое содержание дисциплины
Теория антагонистических игр, теоремы существования седловых точек, свойства оптимальных смешанных стратегий, методы решения матричных и выпуклых непрерывных игр в смешанных стратегиях, приводятся классические модели игр («нападение-оборона» и дуэли), рассматриваются многошаговые игры с полной информацией.
Неантагонистические игры двух и многих лиц. Основные ее разделы: существование и методы поиска ситуаций равновесия (в том числе в смешанных стратегиях для биматричных игр), оптимальные стратегии игрока-лидера в иерархических играх двух лиц.
Теория принятия решений: многокритериальная оптимизация, ядра бинарных отношений, общая модель операции и подход к ее исследованию на основе принципа гарантированного результата, необходимые условия для оптимальных стратегий и некоторые задачи оптимального распределения ресурсов.
Дисциплина «Лаборатория специализации»
Цель освоения дисциплины - формирование навыков анализа временных рядов в среде электронных таблиц, выработка практических навыков построения и анализа математических моделей.
Задачи, соответствующие цели:
- студент должен знать основные понятия и методы, этапы и принципы построение математических моделей технологических и др. процессов, уметь применять полученные знания для анализа и исследования реальных экономических и др. ситуаций;
- студент должен уметь применять основные методы построения математических моделей (метод подобия, принцип максимума и теоремы сравнения, метод осреднения, метод Фурье, методы оценок);
- студент должен закрепить навыки по математическим методам анализа стохастических и детерминированных функций;
- студент должен знать и уметь использовать методы построения и анализа математических моделей для различных задач механики, экономики, социологии на основе использования математического аппарата анализа, вариационных принципов, иерархических цепочек метода аналогий.
Краткое содержание дисциплины
Введение. Постановка задач поискового анализа. Классификация математических методов анализа экспериментальных данных. Поисковый анализ данных. Дисперсионный анализ. Ковариационный и корреляционный анализ. Описательная статистика. Экспоненциальное сглаживание. Анализ Фурье и построение гистограммы. Линейная и нелинейная регрессия. Однофакторный и многофакторный анализ.
Дисциплина «Методы статистических исследований в экономике»
Цель освоения дисциплины – изучение методов статистических исследований и возможностей их применения для решения различного рода задач в экономике.
Задачи, соответствующие цели:
- ознакомление с теоретическими аспектами методов статистических исследований;
- ознакомление со спектром прикладных задач экономики, решаемых с использованием методов статистических исследований.
После прохождения курса студент должен
-
- уметь осуществлять группировку экономических показателей; проводить построение и статистический анализ однофакторных линейных и нелинейных моделей; осуществлять расчеты в части выборочного наблюдения; проводить анализ экономических показателей с использованием индексного метода; проводить построение и статистический анализ многофакторных линейных моделей; применять непараметрические методы обработки экономической информации; проводить расчеты показателей динамики экономических явлений и осуществлять их интерпретацию;
- иметь навыки применения методов статистических исследований в экономических исследованиях.
Краткое содержание дисциплины
Общее понятие о статистической методологии. Статистика как наука. Предмет статистики. Категории статистики.
Статистическое наблюдение. Статистическое наблюдение и его задачи. Формы и программа статистического наблюдения. Виды статистического наблюдения. Ошибки статистического наблюдения.
Статистическая сводка и графический метод в статистике. Понятие и методологические вопросы группировки. Правила составления статистических таблиц. Основные элементы и классификация графиков.
Обобщающие статистические величины. Понятие обобщающих статистических величин. Виды абсолютных и относительных величин. Средние величины. Показатели вариации.
Выборочный метод в статистических исследованиях. Понятие о выборочном наблюдении. Ошибки наблюдения и способы распространения выборочных данных. Необходимая численность выборки. Способы формирования выборочной совокупности.
Статистическое изучение динамики социально-экономических процессов. Ряды динамики, их виды и структура. Показатели, характеризующие тенденцию динамики. Выявление и характеристика основной тенденции развития. Приемы изучения сезонных колебаний. Прогнозирование на основе временных рядов.
Индексный метод в статистических исследованиях. Понятие об индексах. Индексы количественных и качественных показателей. Индексы в экономическом анализе.
Статистические методы изучения взаимосвязи. Корреляционные связи, их характер и формы. Статистические методы выявления наличия взаимосвязи между признаками. Показатели степени тесноты связи между признаками. Методика оценки и практического применения результатов корреляционного анализа.
Дисциплина «Экономико-математические модели»
Цель освоения дисциплины – формирование теоретических знаний о принципах построения экономико-математических моделей и получение практических навыков в управленческой подготовке и экономическом обучении.
Задачи, соответствующие цели:
- создание у студентов необходимого уровня подготовки для анализа эффективности экономических информационных систем и их отдельных компонент методами экономико-математи-ческого моделирования;
- практическое освоение студентами способов применения экономико-математических моделей в системах управления экономического назначения.
После прохождения курса студент должен:
- знать область применения экономико-математических моделей;
- уметь осуществлять сбор данных, необходимых для построения модели; проводить предварительный анализ экономических показателей; самостоятельно работать с выбранным методом экономико-математического моделирования; конструировать модель, необходимую для изучения некоторой проблемы; описывать поведение модели; оценивать результат применения конкретной экономико-математической модели;
-
вых информационных технологий.
Краткое содержание дисциплины
Линейное программирование. Разновидности экономико-математических моделей и методов. Основная задача линейного программирования. Симплекс-таблица. Симплекс-метод. Двойственные задачи линейного программирования.
Нелинейное программирование. Нелинейное программирование. Графические методы решения задач. Метод Лагранжа. Градиентные методы.
Дробно-линейное программирование.
Целочисленное программирование.
Динамическое программирование. Динамическое программирование. Постановка задачи. Задача о распределении ресурсов. Задача замены оборудования. Формулировка задачи динамического программирования в общем виде.
Дисциплина «Дискретная оптимизация»
Цель освоения дисциплины. Дискретная оптимизация и одна из ее главных составляющих - целочисленное линейное программирование - составляют теоретическую базу для исследования и решения большинства экстремальных задач математической кибернетики, завоевывающей все более расширяющую прикладную базу (экономика, информационные модели и проч.). Цель курса состоит в изучении таких моделей, способов их построения и анализа.
Задачи, соответствующие цели:
- ознакомление студентов с математическими моделями, приводящими к решению задач линейного и целочисленно-линейного программирования, методами решения этих задач,
- изучение строения и свойств множества целочисленных решений систем линейных неравенств, уравнений и сравнений,
- иллюстрация понятий "теории сложности алгоритмов", позволяющих выделить подклассы задач, имеющих эффективные алгоритмы.
Краткое содержание дисциплины
Примеры задач дискретной оптимизации (о коммивояжере, о назначениях, о рюкзаке, экстремальные задачи на графах и булевых функциях). Их сведение к задачам целочисленного линейного программирования (ЗЦЛП). Общие сведения о методах решения задач: методы отсечения, комбинаторные методы, приближенные методы. Целочисленные многогранные множества.
Схема метода для общей задачи дискретного программирования, метод Ленд и Дойг для задачи частично целочисленного линейного программирования, метод Ленд и Дойг для задачи о ранце, применение метода ветвей и границ для задачи коммивояжера, некоторые вопросы вычислительной реализации алгоритмов с древовидной схемой поиска оптимального решения, задача об одномерном ранце, задача о многомерном ранце, алгоритм Данцига для линейной одномерной задаче о ранце. Алгоритмы приближенного решения задачи о многомерном ранце, алгоритмы улучшения начального решения.
Задача о распределении ресурсов между проектами, задача о ранце, задача о минимизации суммы функций двух переменных, принцип оптимальности Беллмана.
Приближенные методы и алгоритмы в дискретном программировании. Постановка задачи о поиске приближенного решения и некоторые общие вопросы.
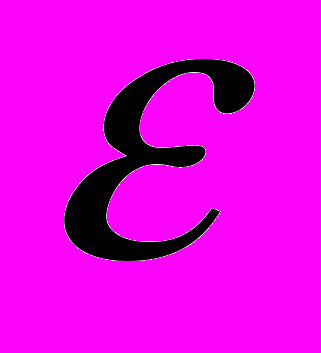-оптимальный алгоритм «ветвей и границ» для задачи о ранце.Дисциплина «Введение в математическое моделирование»
Цель освоения дисциплины: формирование теоретических знаний о принципах постро-ения математических моделей.
Краткое содержание дисциплины
П
онятие математической модели. Моделирование как метод научного познания. Основные этапы математического моделирования. Общие принципы построения математических моделей. Регрессионные модели. Статические регрессионные модели. Динамические регрессионные модели 1 и 2 порядка. Модель сигнала и устройства в представлении Фурье. Компьютерная реализация регрессионных моделей. Модели систем с сосредоточенными параметрами. Статистическое моделирование систем. Метод Монте-Карло. Моделирование случайных событий. Технология вычислительного эксперимента. Использование моделирования при исследовании, проектировании и эксплуатации систем обработки информации и управления. Адекватность и эффективность модели. Примеры построения математических моделей.
Дисциплина «Объектно-ориентированное программирование»
Цель изучения дисциплины - ознакомить студентов с основами объектно-ориентирован-ного программирования как современного подхода к программированию и подготовить их к решению различных задач с использованием различных методов программирования.
Задачи, соответствующие цели:
- студенты должны знать: основы теории и общие методологические принципы объектно-ориентированного программирования, методы проектирования, разработки и создания программных продуктов с применением объектно-ориентированного программирования;
- студенты должны уметь ставить задачи на разработку программного обеспечения с использованием ООП и решать их; знать особенности объектно-ориентированных возможностей различных языков программирования и программных систем.
Краткое содержание дисциплины
Введение в объектно-ориентированное программирование.
Основные составляющие объектно-ориентированного программирования.
Место объектно-ориентированного программирования в мире программ и техники. Методология подготовки и написания объектно-ориентированных программ.
Объектно-ориентированное программирование в языке С++.
Разработка приложений в среде Windows.
Обзор языков положенных в основу Visual C++.
Элементы графического проектирования программных систем.
Обзор пакетов разных фирм, основанных на объектно-ориентированном программировании
Дисциплина «Имитационное моделирование экономических систем»
Цель освоения дисциплины: формирование теоретических знаний о принципах построения систем имитационного моделирования и получение практических навыков в управленческой подготовке и экономическом обучении.
Задачи, соответствующие цели:
- создание необходимого уровня подготовки для анализа эффективности экономических информационных систем, компьютерных сетей и их отдельных компонент методами имитационного моделирования,
- формирование практического освоения способов применения имитационных моделей в системах управления экономического назначения,
- получение базовых знаний в области имитационного моделирования,
- ознакомление с основами математического анализа моделей, необходимого для решения теоретических и практических задач;
- освоение методологии и технологии моделирования (в первую очередь компьютерного) при исследовании, проектировании и эксплуатации систем обработки информации и управления;
- развитие логического мышления;
- привитие умения самостоятельно изучать научную литературу по математике и ее приложениям;
- повышение общего уровня математической культуры;
- выработка навыков математического исследования прикладных вопросов.
Краткое содержание дисциплины
- основы имитационного моделирования;
- графические схемы моделей;
- языковые средства моделирования;
-функциональная структура систем моделирования;
-
математический аппарат, используемый системой имитационного моделирования;
- анализ эффективности вычислительного процесса в информационных системах и компьютерных сетях;
- применение имитационных моделей в системах управления.
В результате изучения дисциплины студент должен:
- знать область применения имитационных обучающих систем; основные методы обучения с использованием имитационных методов активного обучения;
- уметь самостоятельно работать с выбранным методом имитационного обучения; конструировать модель, необходимую для изучения некоторой проблемы; осуществлять сбор данных, необходимых для построения модели; описывать модель на языке, приемлем для используемой ЭВМ; оценивать адекватность модели; осуществлять планирование экспериментов; непосредственно осуществлять имитацию с целью получения желаемых результатов; описывать поведение модели; строить теории и гипотезы, которые смогут объяснить наблюдаемое поведение.
Дисциплина «Основы информатизации управления»
Цель освоения дисциплины: введение студентов в круг одного из разделов современной информатики, изучение методов проектирования систем автоматизации управленческой деятельности государственных и коммерческих структур.
Задачи, соответствующие цели:
- ознакомить студентов с основными типами информационных технологий, с которыми сталкивается менеджер в процессе своей работы,
- ознакомить студентов с основными тенденциями в области разработок систем автоматизации управленческой деятельности, методологии построения этих систем, а также их использования для построения прикладных офисных автоматизированных информационных систем,
- ознакомить студентов с основными принципами сетевого взаимодействия компьютеров в локальных и глобальных сетях. Студенты должны знать основы построения интранет сетей и организацию информационных сетей предприятия с использованием интранет технологий,
- ознакомить студентов с областью применения, основами организации и принципами работы экспертных систем и систем принятия решений с участием экспертов, дать представление о моделях и методах, используемых в области принятия решений,
- ознакомить студентов с проблемами информационной безопасности и основными направлениями их решения; дать представление о принципах и подходах к решению задач защиты информации; выработать навыки разработки политики информационной безопасности, применения современных методов и средств защиты информационных ресурсов предприятий.
Краткое содержание дисциплины
Предмет и основные проблемы управления. Производственная система и производственный процесс. Принципы научного управления предприятием.
Классификация видов управления. Функции управления. Методологические аспекты исследования систем управления. Методы решения управленческих проблем. Методологические инструменты входного контроля. Прогнозирование как функция управления. Методология и организация процесса принятия управленческих решений. Обзор основных подходов к принятию управленческих решений. Методы управленческого воздействия. Целевая ориентация управленческих решений. Виды решений.
Требования к документационному обеспечению управления. Документооборот на предприятии. Общая характеристика и структура системы документационного обеспечения управления. Архитектура систем документационного обеспечения управления.
Информационный характер процесса управления. Понятие информации; виды информации; аспекты информации, современные требования к информации. Адекватность информации. Структура и закономерности протекания информационных процессов; общая характеристика процессов сбора, передачи, обработки и накопления информации. Содержание информационной технологии, как составной части информатики. Общая классификация видов информационных технологий и их реализация в технических областях.
Системный подход к решению функциональных задач и к организации информационных процессов. Принципы и методы проектирования систем управленческой деятельности Общая концепция моделирования систем документационного обеспечения управления Технологическое обеспечение систем документационного обеспечения управления.
Организация электронного документооборота на предприятии. СЭД в России. Основные параметры документов. Процессы электронного документооборота. Регистрация документов. Постановка документов на контроль. Организация маршрутов. СЭД «Евфрат». Автоматизируемые виды деятельности и функции. Требования к аппаратному обеспечению рабочего места пользователя. Требования к программному обеспечению рабочего места пользователя. СЭД «Евфрат». Регистрация документов. Просмотр и редактирование документов. Работа с проектами документов. Назначение персональных прав доступа к документу. Контроль исполнения документов. Работа с поручениями. Работа с согласованиями. Работа с модулем «ДИЗАЙНЕР МАРШРУТОВ». Создание маршрута. Описание элементов маршрута и их свойств.
Анализ стандартов информационной безопасности. Способы и средства защиты информации. Защита информации от компьютерных вирусов.
Дисциплина «Математические модели микро- и макроэкономики»
Цель освоения дисциплины - формирование теоретических знаний о принципах построения математических моделей микро- и макроэкономики, получение практических навыков в управленческой подготовке и экономическом обучении.
Задачи, соответствующие цели:
- создание у студентов необходимого уровня подготовки для анализа эффективности экономических информационных систем и их отдельных компонент методами математических моделей микроэкономики;
- практическое освоение студентами способов применения математических моделей микроэкономики в системах управления экономического назначения.
В результате изучения дисциплины студент должен знать область применения математических моделей микроэкономики; уметь осуществлять сбор данных, необходимых для построения модели; уметь проводить предварительный анализ экономических показателей; самостоятельно работать с выбранным методом экономико-математического моделирования; конструировать модель, необходимую для изучения некоторой проблемы; описывать поведение модели; оценивать результат применения конкретной математической модели микроэкономики.
Краткое содержание дисциплины
Микроэкономика: предмет изучения, объект и методы исследования. Суть математического моделирования в микроэкономике. Транспортная задача. Метод потенциалов. Распределительный метод. Теория графов. Задача о кратчайшем пути. Построение графа наименьшей длины. Транспортные сети. Транспортная задача на графах. Сетевое планирование. Построение сетевого графика. Определение резервов времени. Сокращение директивного срока выполнения работ. Сетевое планирование при случайных временах выполнения работ. Поиск критического пути в сетевом графике. Элементы теории игр. Принцип минимакса. Решение игры в смешанных стратегиях. Решение игр графическим методом. Решение игр методами линейного программирования. Решение игр методом итераций.
Дисциплина «Система поддержки выработки решений»
Цель освоения дисциплины – формирование теоретических знаний и практических навыков решения задач управления и принятия решений в информационных системах.
Предметом изучения дисциплины являются методические основы разрешения проблемных административных ситуаций и создания информационных технологий.
Задачи, соответствующие цели:
- определение роли информационных процессов;
- уяснение методических основ создания информационных систем и технологий;
- рассмотрение методов, процедур и методик проектирования информационных систем;
- учёт особенностей реализации интегрированных информационных технологий в информационной сфере и применения их на практике.
Краткое содержание дисциплины
Введение. Цели и задачи изучения дисциплины. Системы поддержки и принятия решений, основные понятия, классификация. Информационно-обучающая среда по учебной дисциплине.
Структура и инструментальные средства систем поддержки и принятия решений. Управленческая деятельность в условиях телекоммуникаций и информатизации. Информационные аспекты управления. Организационная структура информационных технологий и систем управления. Место процессов обработки информации в управлении. Информационные технологии – инструмент формирования управленческих решений. Информационные технологии управления в корпоративных системах. Программные средства информационных систем административного управления. Системы единого электронного документооборота и делопроизводства.
Технологии принятия решений при многокритериальном выборе вариантов. Целевая функция и функция полезности. Адаптивные процедуры выбора. Метод парных сравнений. Рандомизированные стратегии принятия решений. Назначение и области применения экспертных систем. Инструментальные средства многокритериального выбора.
Поддержка управляющих решений в системах централизованного обслуживания. Системы централизованного обслуживания. Организационные режимы технологий обслуживания. Основные параметры управления обслуживанием. Критерий оптимизации, ограничения. Построение алгоритмов оптимизации. Поиск приближённых и оптимальных решений прикладных задач.
Технологии управления ресурсами и ресурсно-временная оптимизация. Понятие о ресурсах и методах управления ими. Построение графика привлечения возобновляемых и невозобновляемых ресурсов. Проблемные ситуации в распределении ресурсов. Постановка и моделирование задач ресурсно-временной оптимизации. Алгоритмы оптимизации привлекаемых ресурсов и сроков выполнения проекта. Управление ресурсами и циклом реализации проекта.
Алгоритмы в системах поддержки и принятия решений.
Определения и понятия алгоритмов. Представление объектов. Кодирование признаков. Операторы. Схема функционирования алгоритма. Примеры реализации основных операторов.
Информационные системы поддержки и выработки решений. Информатизация задач выработки. Классификация информационных систем . Нормативные документы по проектированию информационных систем.
Приложение 5
АННОТАЦИЯ К РАБОЧЕЙ ПРОГРАММЕ ПРАКТИКИ
В соответствии с базовым учебным планом специальности студенты проходят производственную практику на 3 (3 недели) и 4 курсах (4 недели), преддипломную практику – на 5 курсе (9 недель).
Производственная и преддипломная практики являются важнейшим этапом как профессионального, так и личностного развития будущих специалистов. В процессе их прохождения студенты включаются в производственную деятельность, впервые непосредственно знакомятся с выполнением функций математика, системного программиста. Практика помогает студентам овладеть профессиональными умениями и навыками, осознать научно-теоретические основы работы, закрепляет их теоретическую подготовку, знания из области профильных дисциплин. Практика организуется в соответствии с государственным стандартом высшего профессионального образования в части государственных требований к минимуму содержания и уровню подготовки выпускников специальности 010100 (010101.65) «Математика».
Целью практики является закрепление знаний, полученных студентами в процессе обучения, на основе их практического применения при овладении производственными навыками.
Основные задачи: получить знания и умения в применении современных математических методов и программного обеспечения для решения задач науки, техники, экономики и управления; получить опыт в использования новых информационных технологий в проектно-конструк-торской, управленческой и финансовой деятельности.
Основными принципами организации практики являются следующие:
- усложнение ее содержания и методов организации от курса к курсу;
- связь практики с изучением теоретических курсов;
- единство научно-теоретической обоснованности практики и реальности производственной деятельности предприятия, учреждения или организации.