Geum.ru

И. В. Дробышева кандидат педагогических наук, профессор

Вид материалаДокументы

Содержание


О трансляции программ mathcad и pascal на примере построения фракталов
Подобный материал:
1   ...   9   10   11   12   13   14   15   16   ...   76

О ТРАНСЛЯЦИИ ПРОГРАММ MATHCAD И PASCAL НА ПРИМЕРЕ ПОСТРОЕНИЯ ФРАКТАЛОВ

К.А. Попов

Волгоградский государственный педагогический университет, Волгоград


Межпредметные связи курсов математики и информатики, которые в недавнем прошлом были «предметами одного учителя», поскольку преподавал и математику и информатику в школе, как правило, учитель математики, сейчас дали трещину. Связано это с тем, что от преподавания основ программирования и алгоритмизации с увеличением производительности компьютеров и развитием графических интерфейсов программ информатика довольно быстро перешла к изучению информационных технологий, практически не требующих ни умения программировать, ни знаний математики. Сложившаяся ситуация активно обсуждается в самых разных институтах системы образования [1, 2].

Одним из возможных решений данной проблемы представляется использование математических задач и моделей в качестве заданий по информатике.

Для интеграции математики и информатики можно выбрать любой комплекс задач, требующих алгоритмического подхода к их решению. Это могут быть и построение графиков функций, и задачи численного интегрирования, и решение физических задач с построением математической модели, и т.д. В данной статье мы остановимся на достаточно новой области взаимодействия информатики с математикой: на построении геометрических фракталов. С одной стороны, нас будут интересовать проблемы алгоритмизации процесса построения кривых, а с другой стороны, мы рассмотрим принципы преобразования или адаптации существующего алгоритма (или программного кода) для его использования в других системах программирования. Последнее является особенно существенным шагом, поскольку достаточно сложно найти подходы к преобразованию существующих программ при их переводе на другой язык программирования или при переходе от одной программной оболочки к другой (например, Mathcad – Delphi). Но школьникам умение пользоваться подобными преобразованиями откроет путь к использованию готовых программ, которые можно найти в учебных пособиях и в Internet, адаптируя их под выбранную оболочку или переводя на нужный язык программирования.

Прежде, чем мы приступим к обсуждению проблем построения фрактальных кривых и преобразования полученных программ, остановимся на моментах использования геометрических фракталов в качестве объекта для отработки методов программирования.

Дело в том, что существует несколько вариантов построения фрактальных кривых, причем все они легко алгоритмизуемы. Для учебных целей лучше всего подходит метод последовательного построения поколений. Он состоит в следующем. В качестве нулевого поколения при построении простейших кривых берется отрезок, длина которого может быть произвольной.

Построение первого поколения кривой является основным шагом и определяет конечный вид кривой. Это связано с тем, что последующие поколения строятся по тому же алгоритму, используя для преобразования отрезки, полученные предшествующими поколениями. Так, например, при построении кривой Леви (Levy) первым поколением являются два катета равнобедренного прямоугольного треугольника, построенного на отрезке нулевого поколения, как на гипотенузе.

Для построения первого поколения достаточно знать координаты точек начального отрезка и по ним рассчитать координаты новой точки. Для кривой Леви метод получения новых координат приведен в статье [3].

Так у нас получается из одного отрезка два новых. Каждый из них становится аналогом нулевого поколения при построении следующего. В идеальном случае истинная фрактальная кривая должна получаться при построении поколения с бесконечно большим номером, то есть полученная ломаная линия должна содержать бесконечно много вершин. Очевидно, что программа не может работать бесконечно долго, иначе алгоритм теряет одно из своих основных свойств – результативность.

Результатом работы программы, строящей фрактальную кривую, должна стать ломаная линия, отражающая поколение кривой с максимально большим номером. Номер конечного поколения существенно зависит от производительности компьютера и среды, в которой реализуется алгоритм построения.

Если мы будем продолжать построение новых поколений, они будут давать более смазанную картину. Поэтому следует соблюдать определенный баланс между номером поколения и наглядностью отображения кривой на экране монитора.

Таким образом, использование метода последовательного построения поколений фрактальной кривой требует от школьника достаточно хороших знаний геометрии (метод координат или векторный метод) и умений строить алгоритм при помощи циклов и последовательного выполнения операций. Из основных структур программирования здесь не задействован только условный оператор.



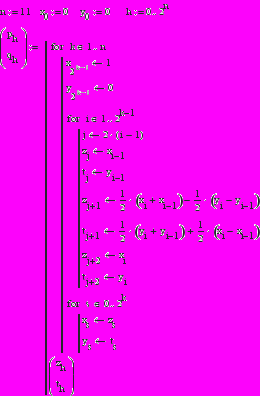
Если мы построим кривую Леви средствами программирования оболочки Mathcad, то у нас получится листинг программы [3]. Данная программа не требует специальных команд для управления выводом графика на экран. Достаточно построить стандартный график зависимости переменной q от p.



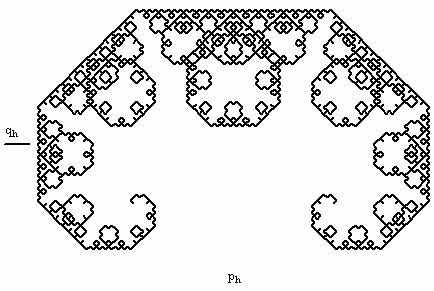
Построив кривую Леви средствами Mathcad, можно перейти к проблеме преобразования данной программы для построения кривой с использованием программы на языке Pascal.

Здесь мы сталкиваемся с несколькими интересными нюансами. Во-первых, необходимо в блоке описаний (в преамбуле) определить размеры массивов, которые мы будем использовать для описания координат точек кривой. Pascal, как программа, работающая в режиме эмуляции DOS, не оперирует всей оперативной памятью компьютера, поэтому мы ограничимся построением одиннадцатого поколения кривой, что потребует 211 + 1 = 2049 точек. Во-вторых, в библиотеке Pascal нет показательной функции. Для этого определяется функция pow(x) = 2x, которая у нас использовалась в программе Mathcad. И, наконец, поскольку программа должна выводить кривую на экран, то в коде должен присутствовать оператор инициализации графики и команды рисования кривой по точкам.


program Levy_Curve;

uses CRT, graph;

var

a,b,k,i,j,n:integer;

x,y,z,t:array[0..2048] of real;

function pow (x:integer) : integer;

var i,r:integer;

begin

r:=1;

for i:=1 to x do r:=2*r;

pow:=r

end;

begin

a:=detect;

initgraph (a,b,' ');

n:=11; x[0]:=0; y[0]:=0;

for k:=1 to n do

begin

x[pow(k-1)]:=1;

y[pow(k-1)]:=0;

for i:=1 to pow(k-1) do

begin

j:=2*(i-1);

z[j]:=x[i-1];

t[j]:=y[i-1];

z[j+1]:=0.5*(x[i]+x[i-1])-0.5*(y[i]-y[i-1]);

t[j+1]:=0.5*(y[i]+y[i-1])+0.5*(x[i]-x[i-1]);

z[j+2]:=x[i];

t[j+2]:=y[i]

end;

for i:=0 to pow(k) do

begin

x[i]:=z[i];

y[i]:=t[i]

end;

end;

MoveTo(170,350);

for i:=1 to pow(n) do

LineTo(170+round(300*x[i]),350-round(300*y[i]));

ReadKey;

CloseGraph;

end.


Легко заметить, что программный код в Pascal отличается от программы в Mathcad лишь наличием блока описания переменных и необходимостью управления выводом результата вычислений на экран. Основной же блок расчета координат претерпел изменения лишь в синтаксисе команд.

Таким образом, преобразование программы из Mathcad в Pascal заключается в адаптации кода путем перевода команд и добавлении блоков описания переменных и вывода графики на экран монитора. Следует отметить, что обратная трансляция программного кода из Pascal в Mathcad требует выполнения практически аналогичных процедур, хотя и требующих некоторой модификации. Поэтому, при необходимости формирования умений перевода программ из одной среды в другую, желательно предлагать учащимся оба варианта трансляции.


Литература
  1. Бешенков С. А., Кузнецова Л. Г., Шутикова М. И. Математика и информатика: поиск точек соприкосновения // Информатика и образование. 2006. № 10. С. 3-5.
  2. Современные проблемы преподавания математики и информатики: сб. науч. ст. по итогам III Междунар. науч.-метод. конф. – Волгоград: Перемена, 2006.
  3. Попов К. А. Векторы, фракталы и компьютерное моделирование // Математика в школе. 2006. № 8. С. 56-61.