И. В. Дробышева кандидат педагогических наук, профессор

Вид материала

Документы

Содержание Вектор, координатный метод и компьютер

Подобный материал:

• Федеральными Государственными Требованиями детство примерная основная общеобразовательная, 3629.29kb.
• Федеральными Государственными Требованиями детство примерная основная общеобразовательная, 7829.77kb.
• Декан, кандидат педагогических наук, доцент Е. В. Шустова Доктор педагогических наук,, 538.89kb.
• Программа воспитания и обучения в детском саду, 3936.51kb.
• Программа воспитания и обучения в детском саду, 3919.5kb.
• Программа воспитания и обучения в детском саду, 3924.08kb.
• Программа воспитания и обучения в детском саду, 3718.01kb.
• Л. Р. Муминова доктор педагогических наук, профессор; Е. В. Оганесян кандидат педагогических, 2948.06kb.
• «Слова о Полку Игореве», 3567.27kb.
• Умк занкова Дидактическая система развивающего обучения Л. В. Занкова академик, доктор, 139.44kb.

ВЕКТОР, КООРДИНАТНЫЙ МЕТОД И КОМПЬЮТЕР

К.А. Попов

Волгоградский государственный педагогический университет, Волгоград

Используемый в геометрии координатный метод решения задач легко поддается алгоритмизации, а, следовательно, он может быть реализован в виде компьютерной программы, необходимой для решения большого количества задач одного типа (одно из свойств алгоритмов). Таким образом, если мы сможем предложить учащимся ряд задач, которые могут быть решены методом координат, то их решение может содержать и математическую часть, в которой обосновывается выбор именно этого метода построения, и часть использования программирования. Подобный подход можно найти, например, в статье [1].

В данной статье мы остановимся на возможности построения образов геометрических фигур, получаемых в результате различных вариантов движения плоскости. То есть, нас будут интересовать:

1) параллельный перенос;

2) осевая симметрия (отражение относительно прямой);

3) центральная симметрия (отражение относительно точки);

4) поворот.

Наиболее простой вариант преобразования – параллельный перенос. Поэтому с его рассмотрения удобнее всего начинать решения данного спектра задач.

С точки зрения координатного метода параллельный перенос заключается в прибавлении к значениям координат точек геометрической фигуры соответствующих координат вектора, характеризующего параллельный перенос. Иначе, если параллельный перенос задан вектором 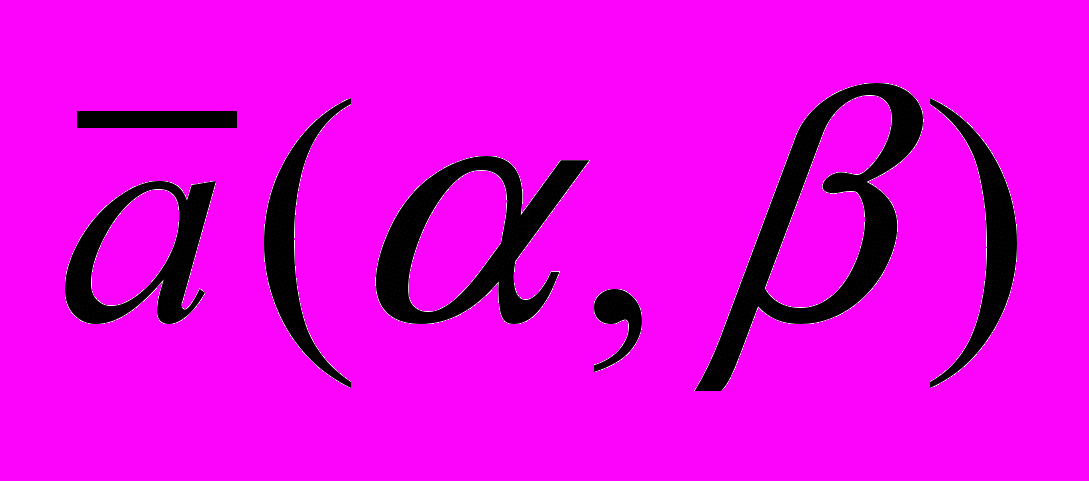, то точка А с координатами 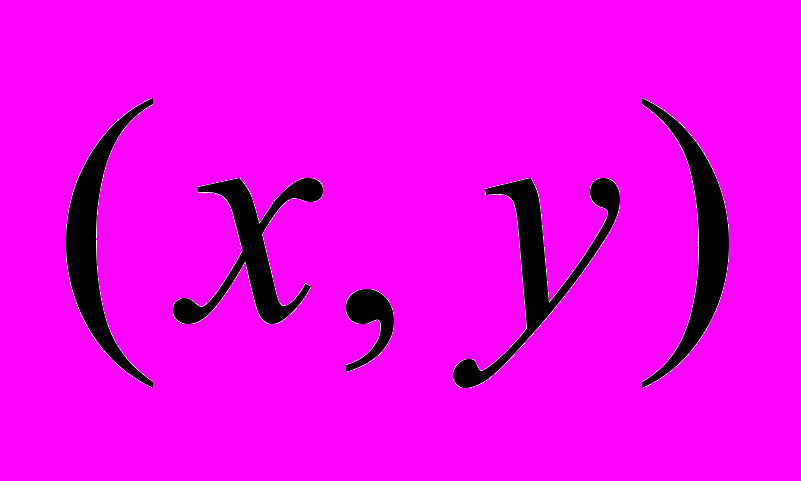перейдет в точку В с координатами .

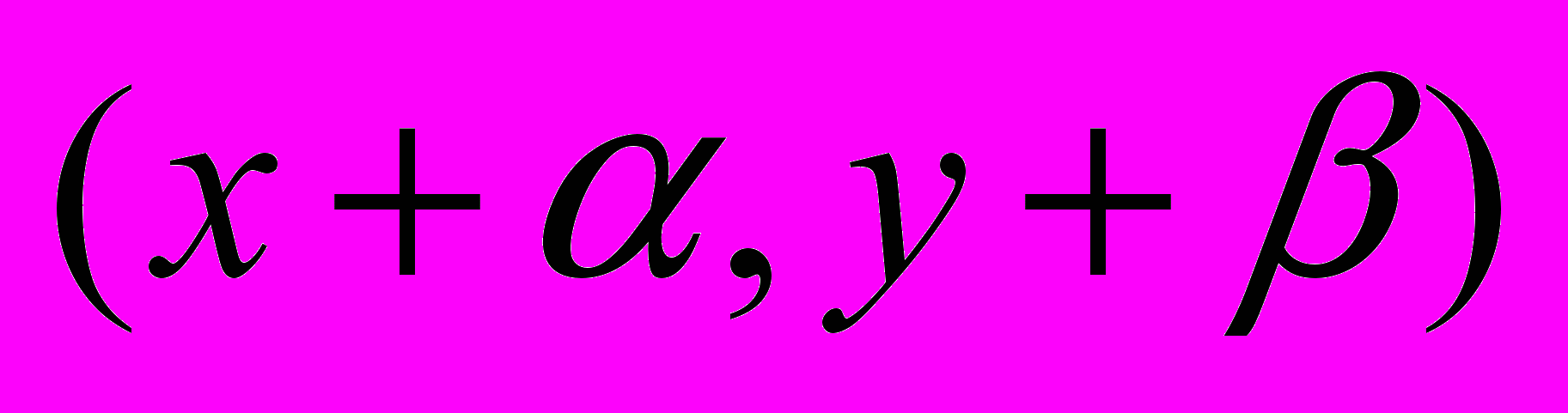Р
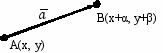
ассмотрим задачу о построении образа квадрата, вершины которого имеют координаты (0, 0), (0, 1), (1, 1), (1, 0) на вектор 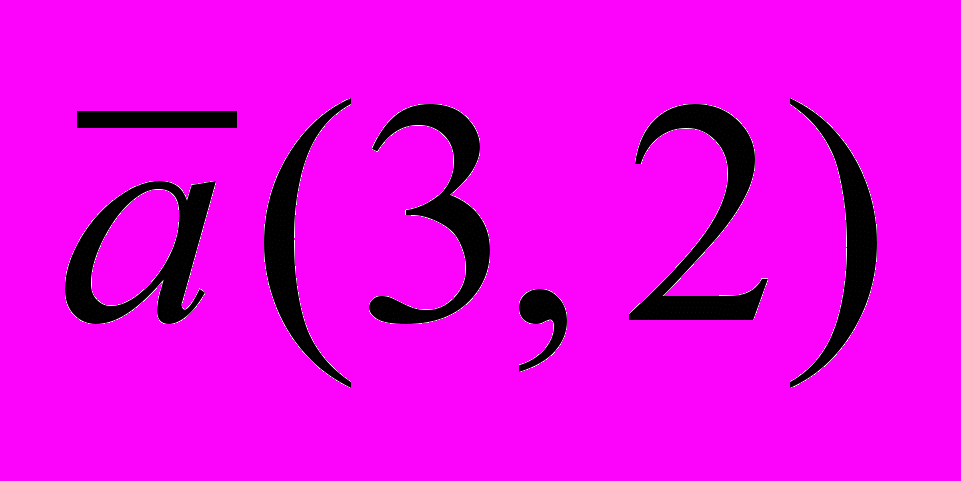. Для этого воспользуемся средствами программирования оболочки Mathcad. Программа должна содержать следующие шаги:

Ввод координат начального массива точек (вершин квадрата), причем точек для расчетов должно быть на одну больше, поскольку в результате построения мы должны получить замкнутую ломаную линию. Для этого первая и последняя точки массива должны быть одинаковыми.

Программа, содержащая цикл расчета координат конечного массива точек (квадрата-образа).

Вывод исходного и получаемого квадратов в качестве графика.

В Mathcad данная программа, построенная на основе примера из [2], будет выглядеть следующим образом:




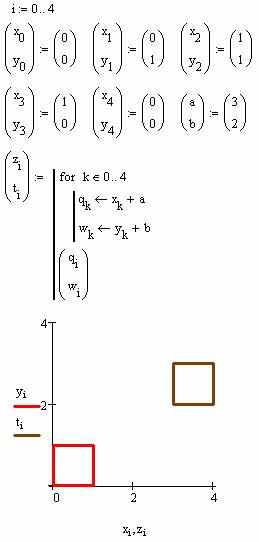
Построение такого несложного программного кода, построенного на основе приведенного примера, обычно не вызывает особых затруднений учащихся, поэтому не требует большого времени на реализацию. Основной же целью использования именно этой простой задачи в качестве исходного пункта для дальнейшего решения задач подобного типа является именно отработка алгоритма решения, так как его понятность не перекрывается ни сложностью математических расчетов, ни трудностями в создании программы.

Рассмотрим следующий вариант движения плоскости: отражение относительно оси. Наиболее простой вариант задачи в данном случае сводится к отражению относительно координатных осей. В таком случае одна из координат точки только меняет знак на противоположный.

Для решения задачи об отражении треугольника относительно оси ординат мы просто несколько модифицируем уже готовую к использованию программу, убрав одну из точек начального массива и изменив формулу преобразования координат.



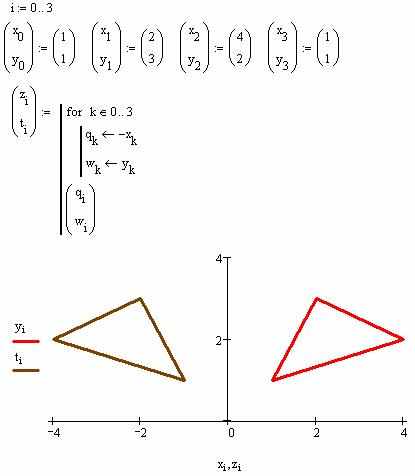
Несколько сложнее с точки зрения математики построить отражение геометрической фигуры относительно произвольной оси.

Пусть нам дана прямая а, описываемая уравнением 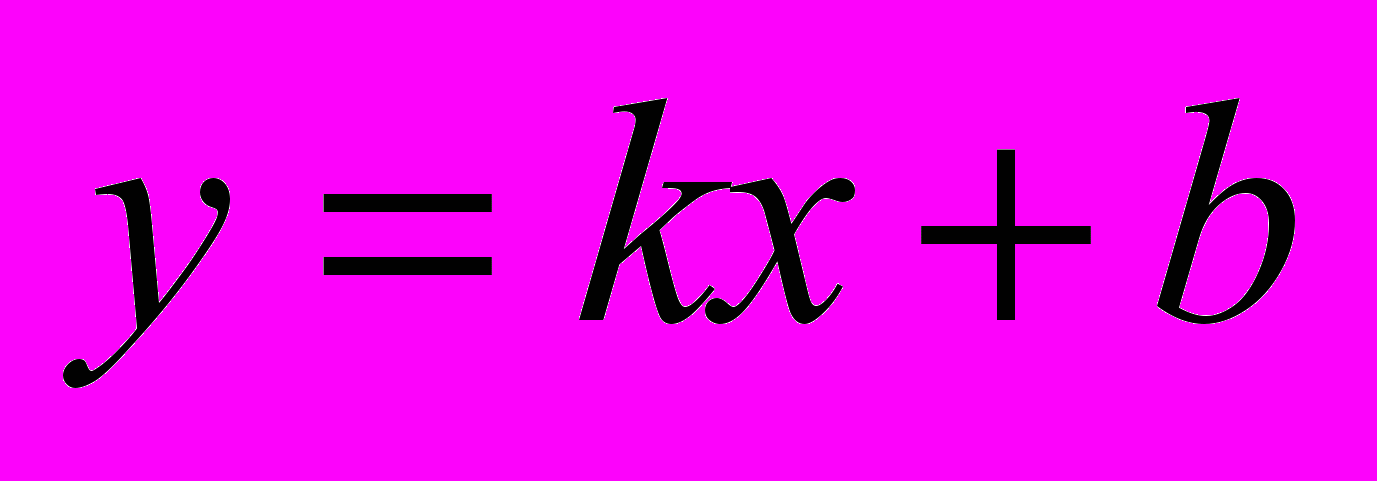. Найдем образ точки А с координатами 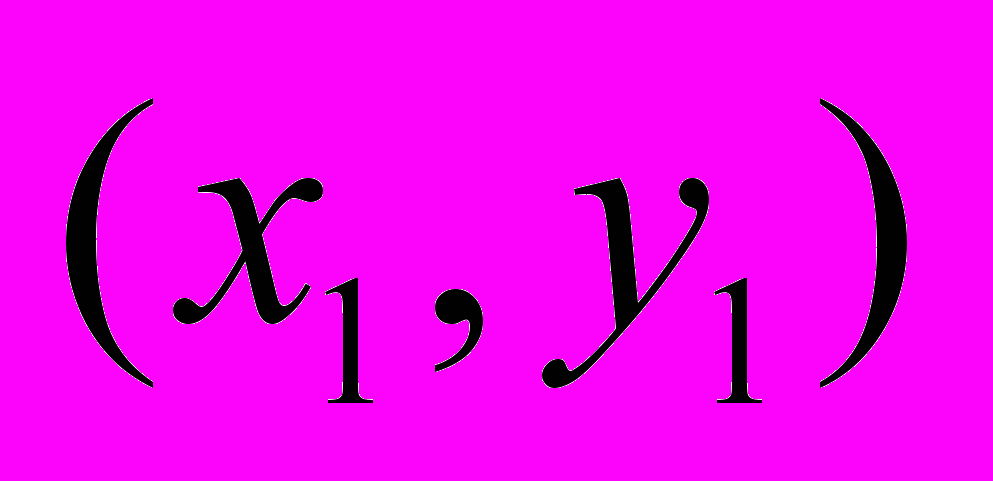. Преобразование координат точки А даст нам общую форму преобразования всех точек плоскости при отражении относительно выбранной нами прямой.

Предположим, выбранная нами точка А переходит в точку В с координатами 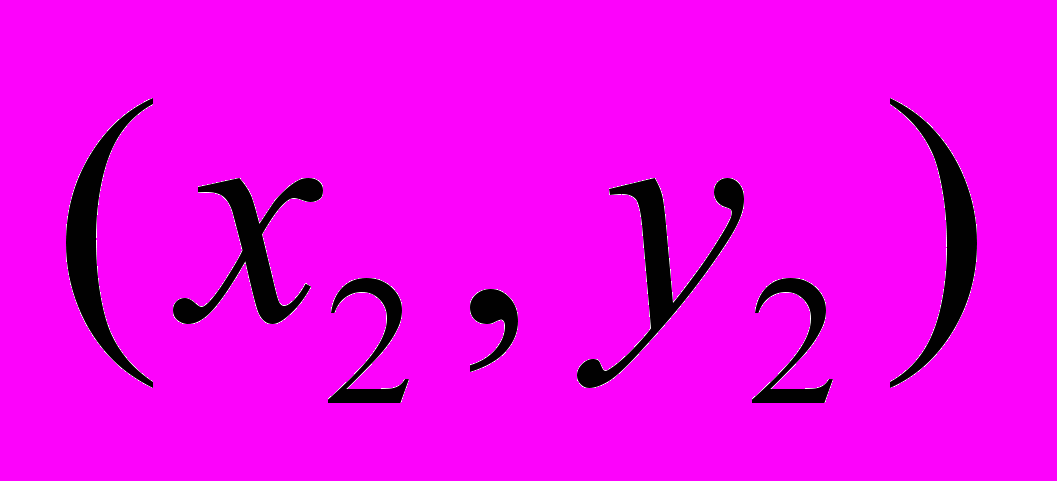. Тогда можно сделать два вывода. Во-первых, через точки А и В можно провести прямую b, перпендикулярную прямой а. Во-вторых, точки А и В будут равноудаленными от точки пересечения прямых а и b. По этим двум выводам необходимо построить систему двух уравнений для определения координат точки В.

Известно (или легко показать), что прямая, перпендикулярная прямой а будет иметь формулу 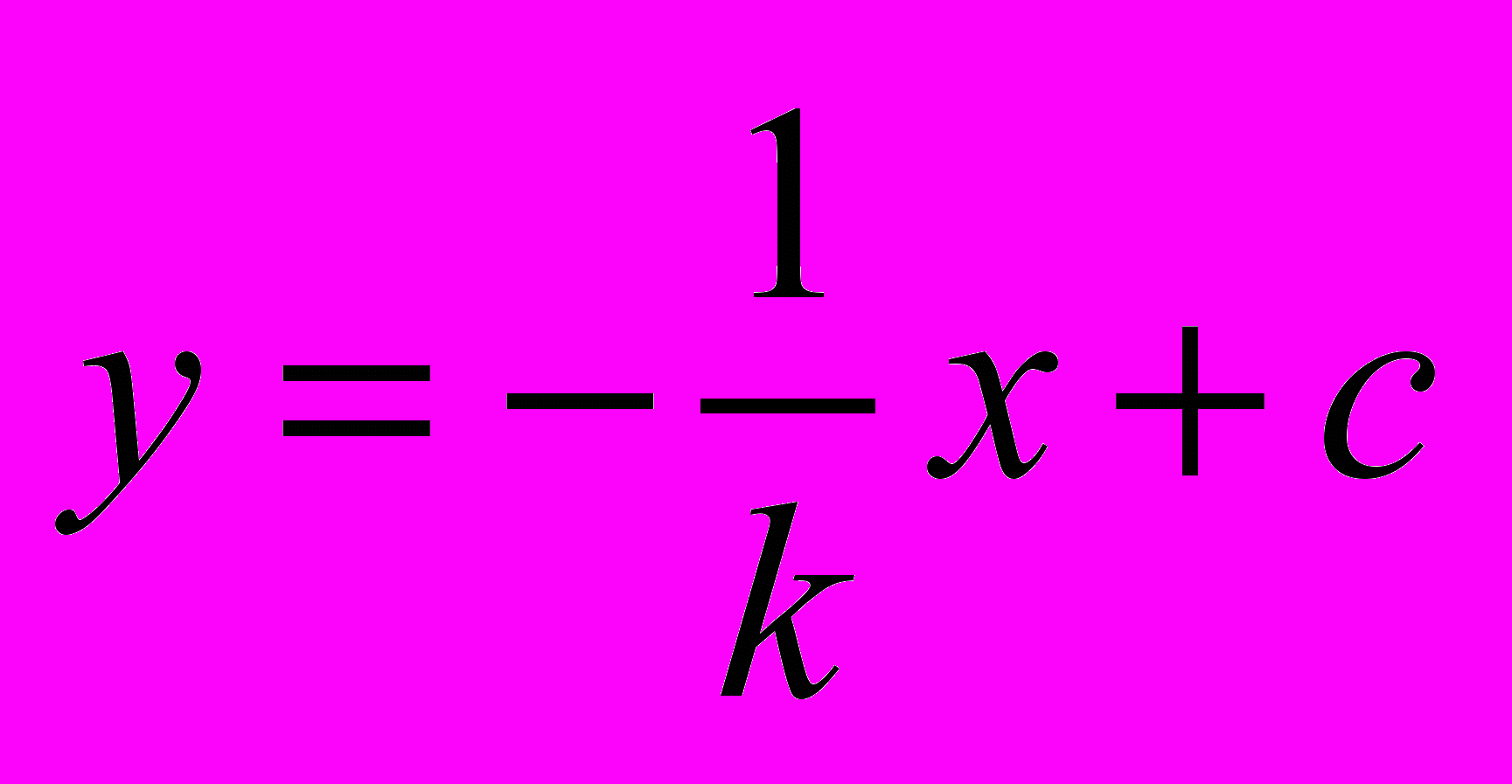. Поэтому для определения прямой b необходимо только узнать значение константы с. Для этого подставим координаты точки А в уравнение прямой и получим

.

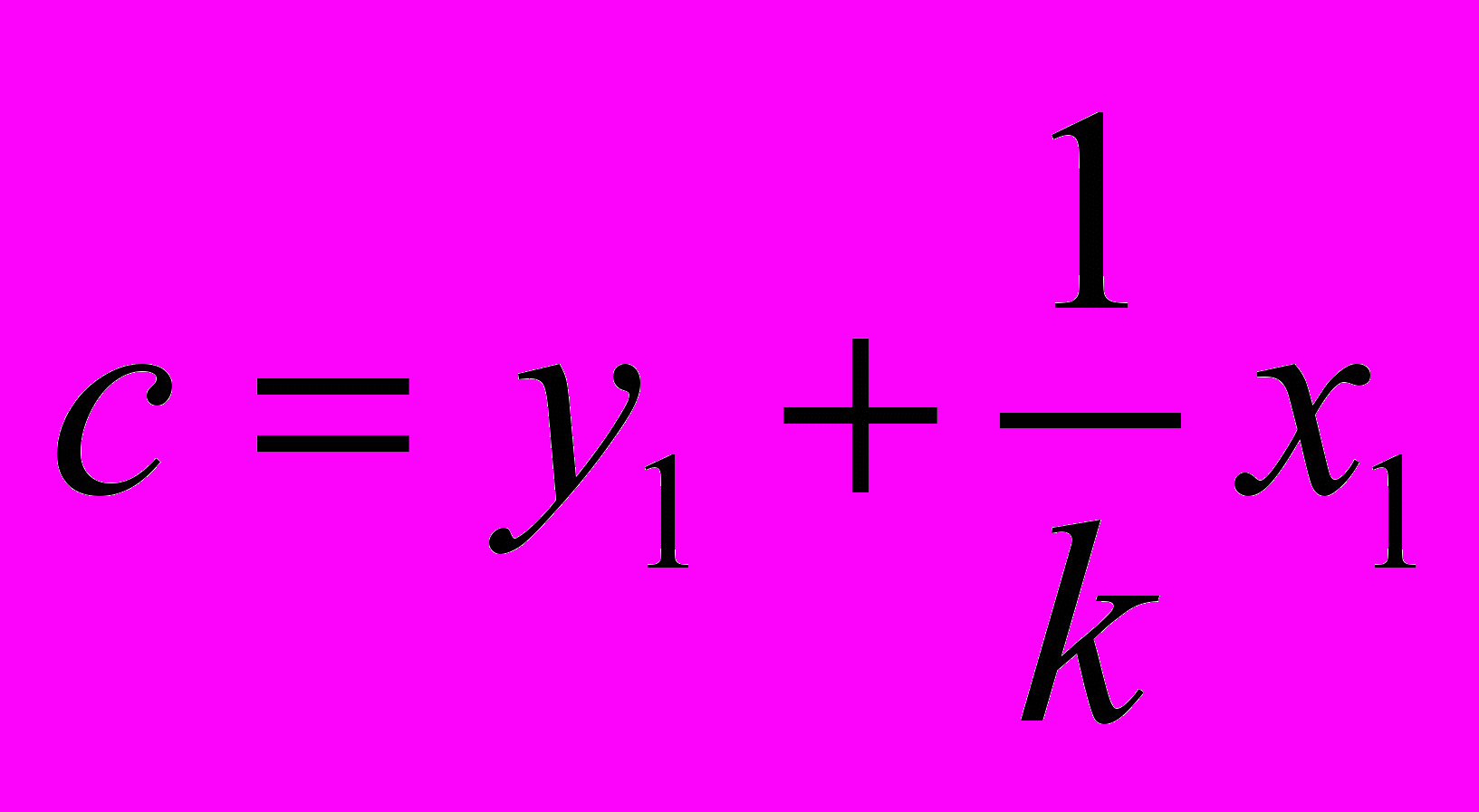Таким образом, получаем уравнение прямой b в виде

.

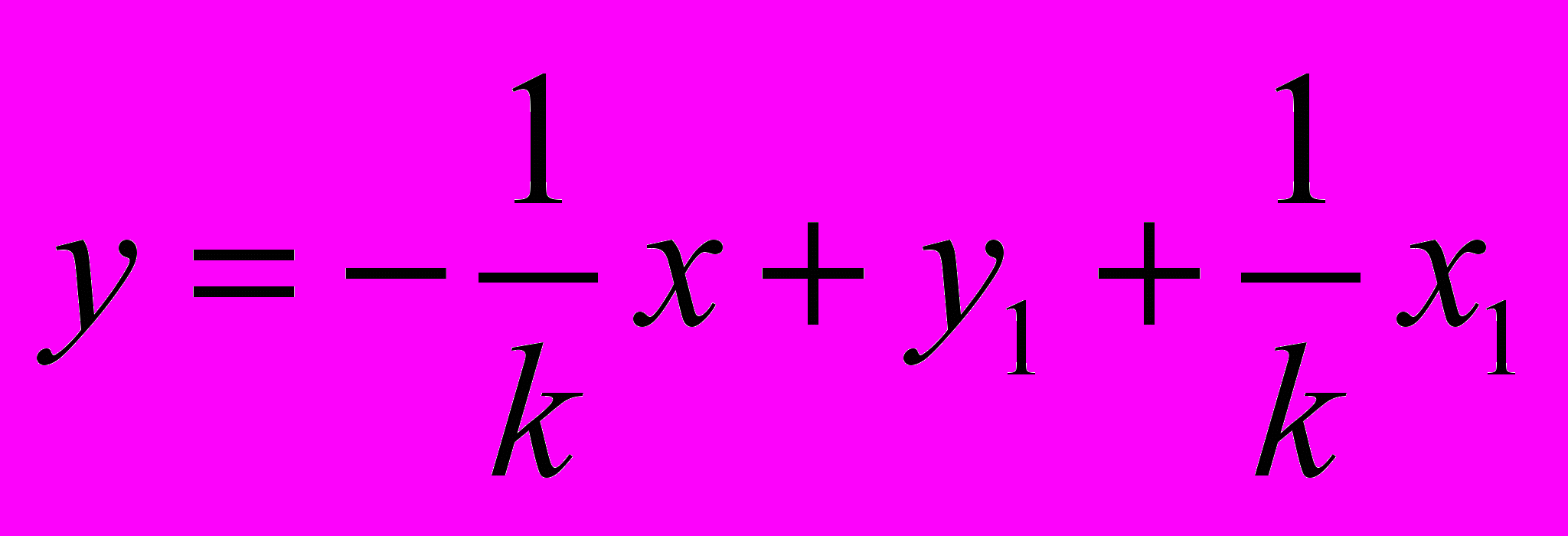Теперь можно найти координаты точки пересечения прямых а и b. Для этого приравняем правые части уравнений прямых

,

,

,

.

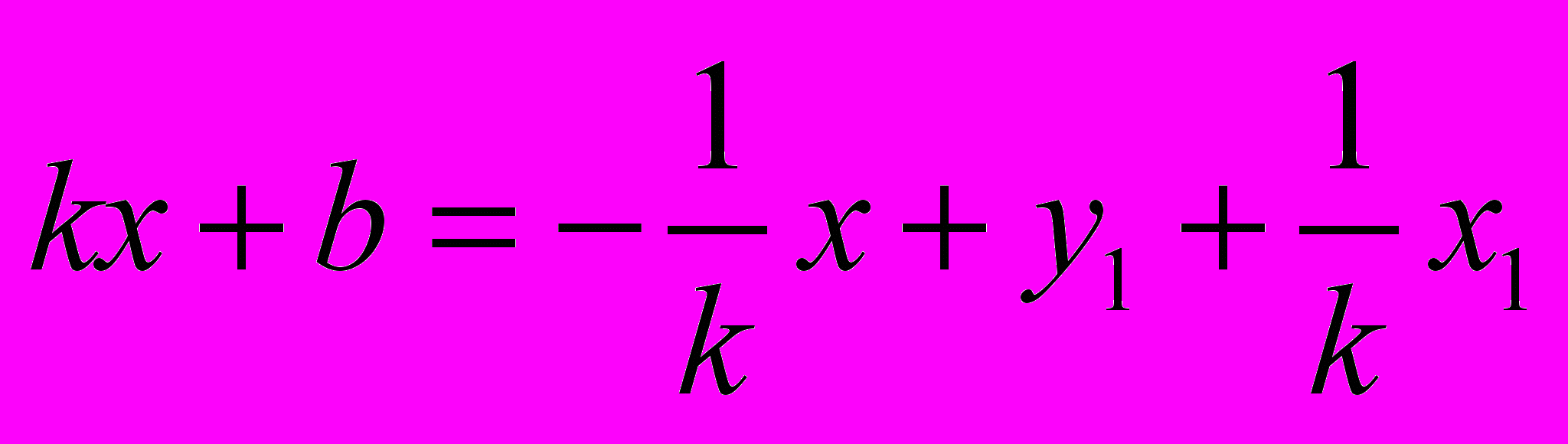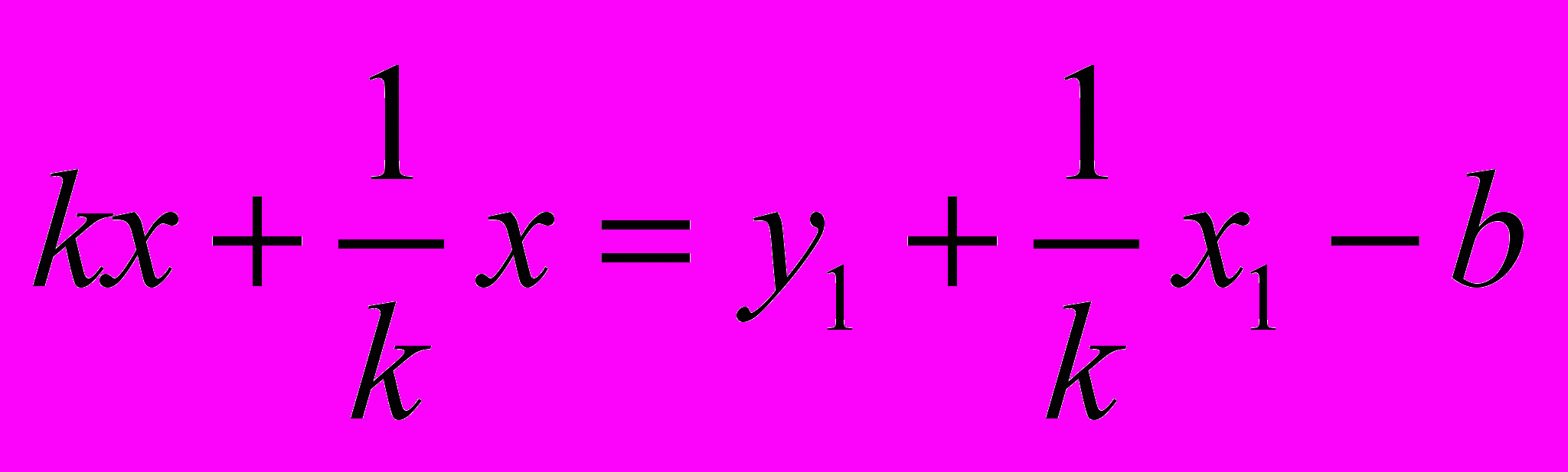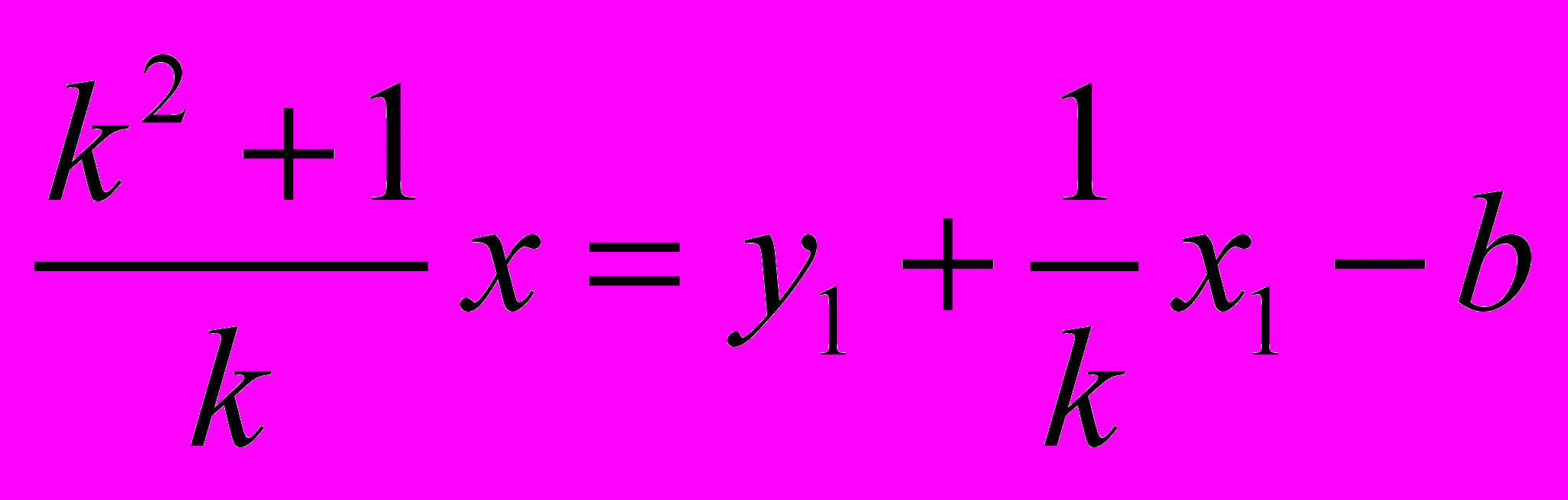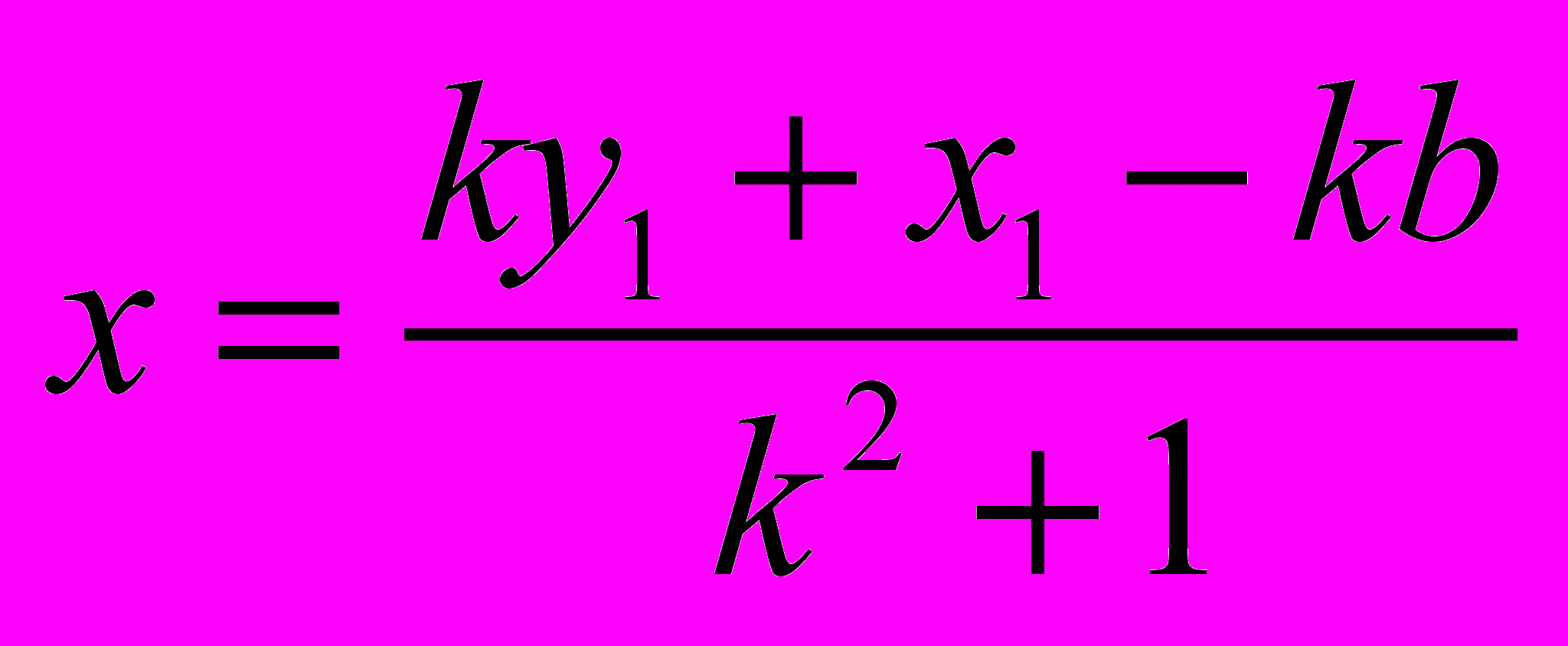Получаем точку Z с координатами.

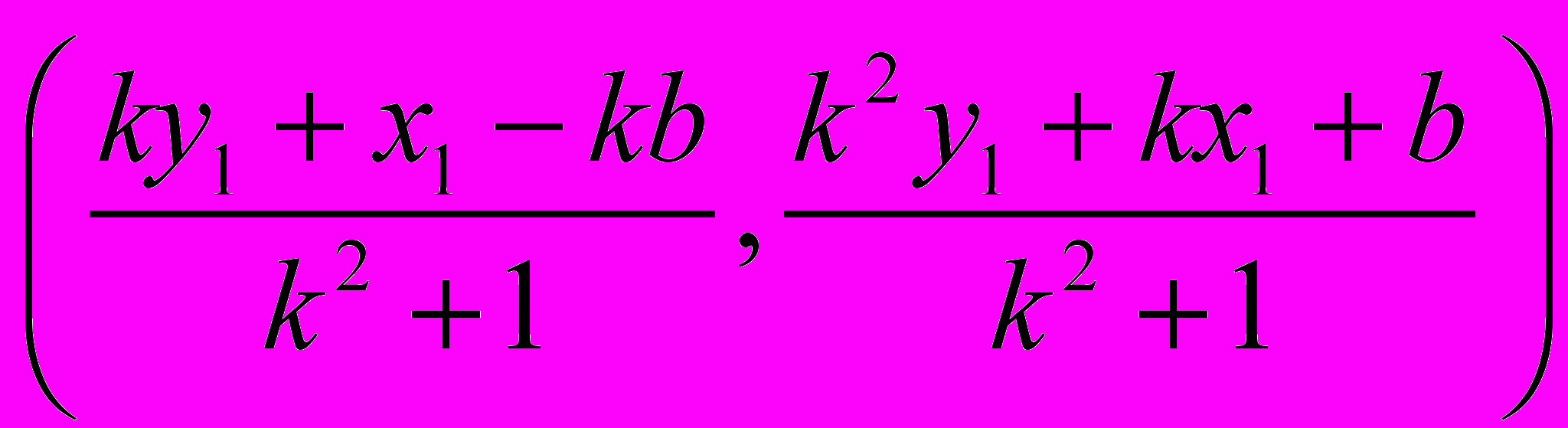Так как 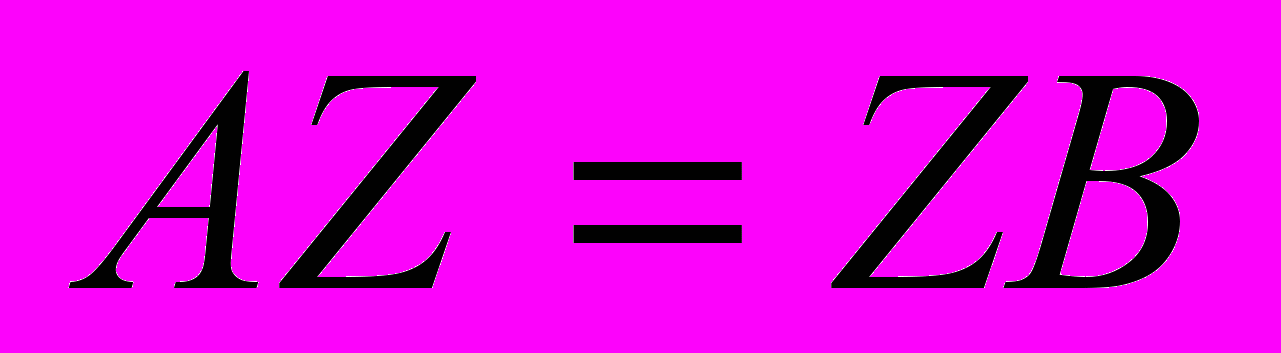, то 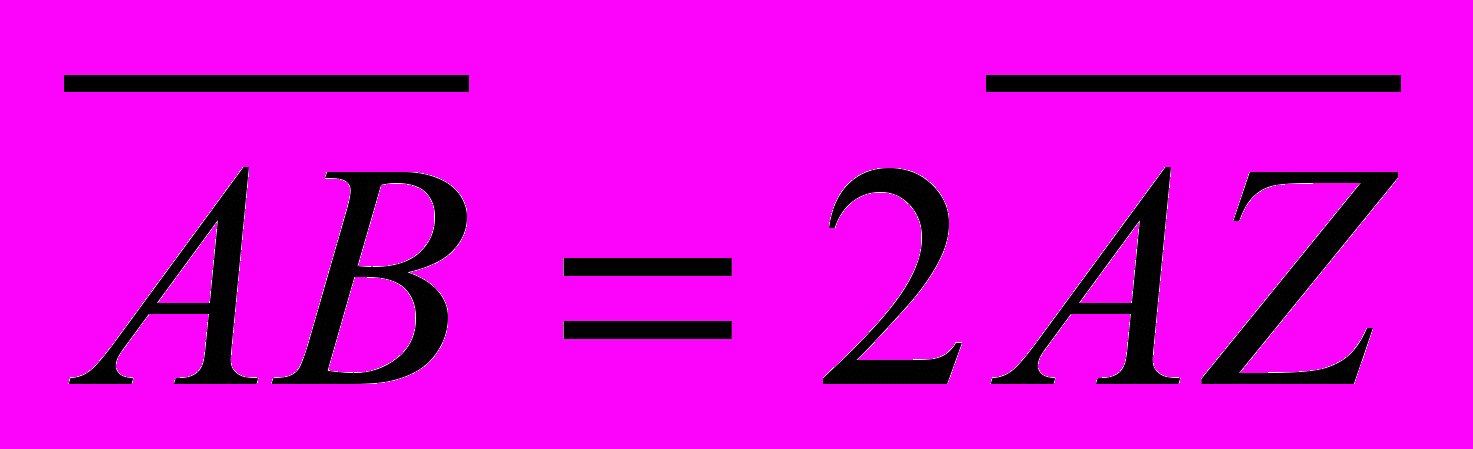. Из данного условия мы можем определить координаты точки В.

,

,

,

.

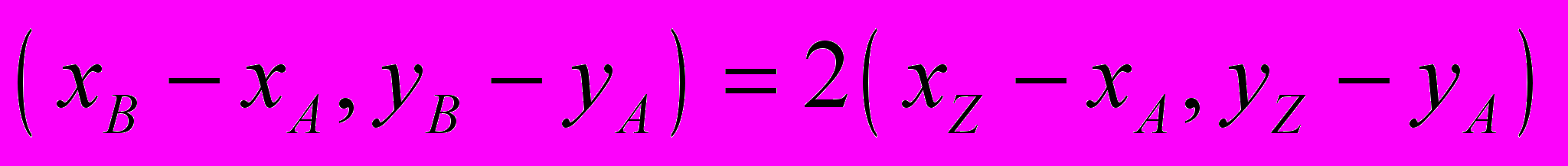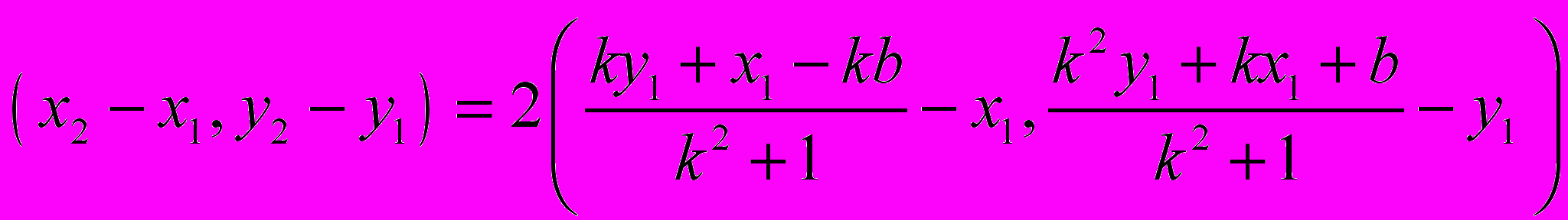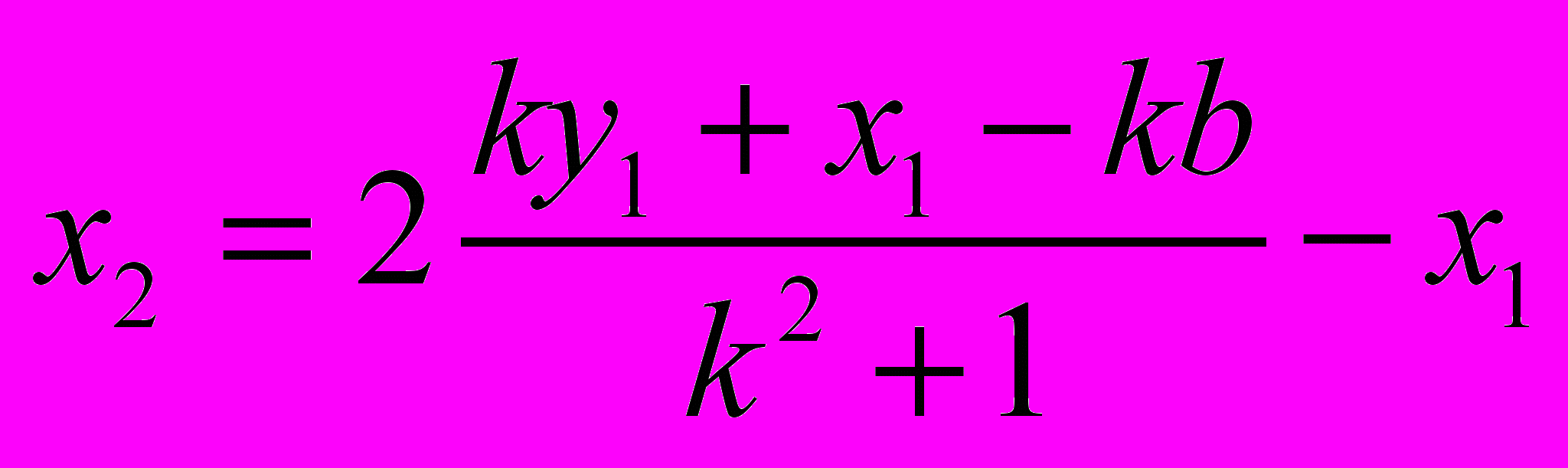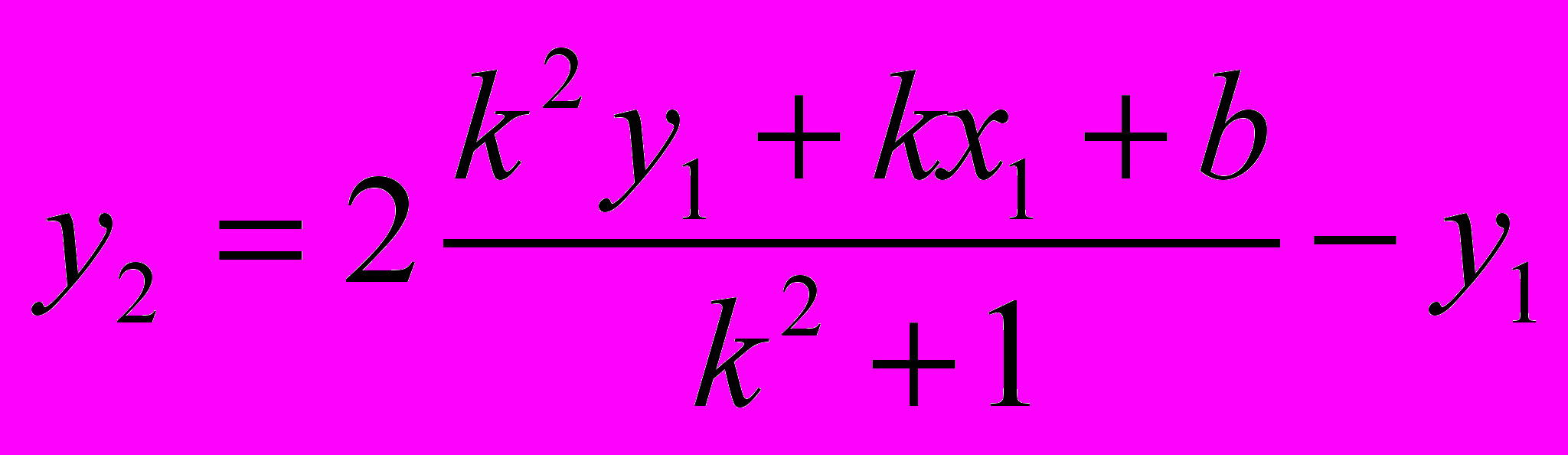Получив условия преобразования координаты точки А в точку В, можно приступать к модификации программы Mathcad для решения задач построения образов геометрических фигур при отражении от произвольной прямой. В качестве примера рассмотрим отражение уже известного нам из предыдущей задачи треугольника относительно прямой 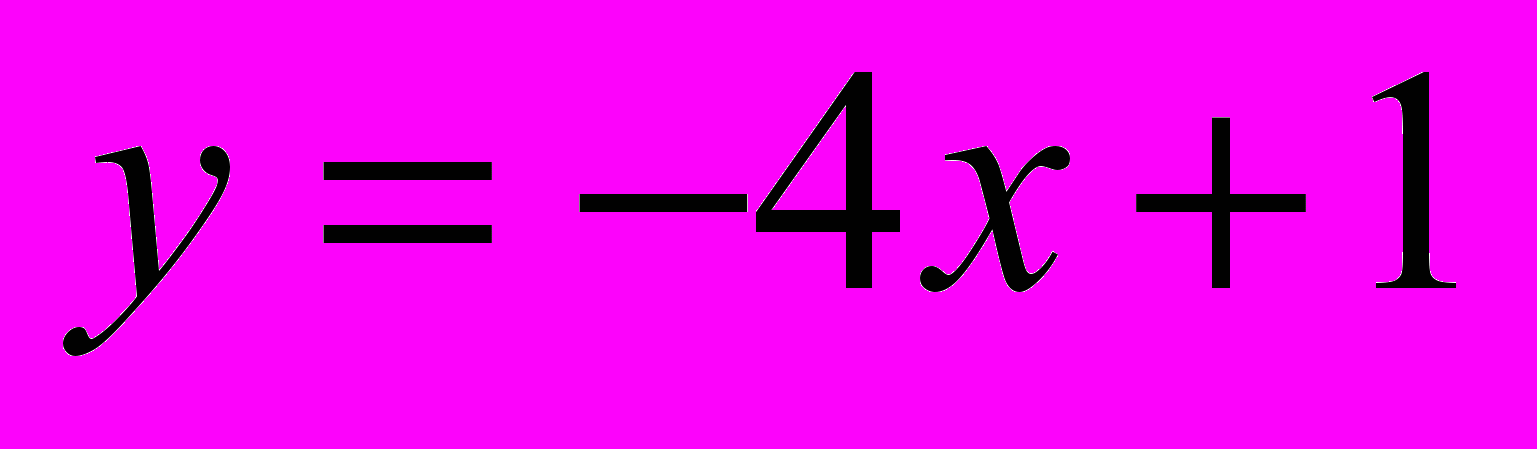. Листинг программы Mathcad будет следующим: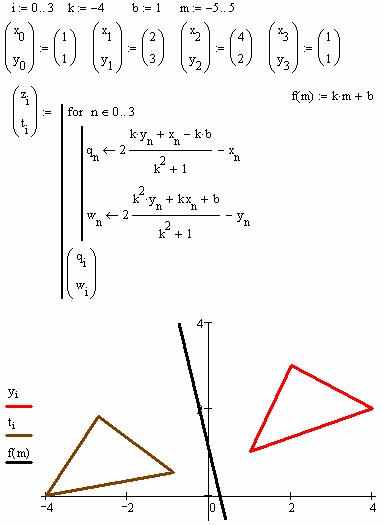



Легко заметить, что основная часть программы не претерпела изменений. Существенно изменился только блок преобразования координат.

Очевидно, что в данной задаче основной акцент уже сделан на математическую сторону вопроса, поскольку программа расчета была уже практически полностью готова. Следовательно, здесь и в последующих задачах во главу угла будет поставлена математика, а информатика будет лишь помогать, повышая наглядность полученного результата решения.


Литература

1. Попов К. А. Векторы, фракталы и компьютерное моделирование // Математика в школе. 2006. № 8. С. 56-61.
   
2. Попов К. А. Mathcad 11. Дополнительный курс: учеб.-метод. пособие. – Волгоград: Перемена, 2006.