Математика: наука
| Вид материала | Документы |
- Колмогоров Андрей Николаевич, 563.58kb.
- Задачи и упражнения по математическому анализу для втузов. Под ред. Б. П. Демидовича., 19.39kb.
- Византийская математика, 186.7kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Расшифровка : Математика, 146.94kb.
- Что такое прикладная математика?, 81.59kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
- Программа Фестиваля Мероприятия мгу им. М. В. Ломоносова, 971.43kb.
22. Восстановление в среднем квадратическом относительно меры Банаха решений задачи Дирихле для уравнения Пуассона
(Международ. Конф. "Функциональные пространства, теория приближений, нелинейный анализ", посвящ. 90-летию академика С.М. Никольского, Москва, 27 апреля-3 мая 1995 г., Тез. докл., стр. 269-270)………….……189
В одном докладе соединены мера Банаха, уравнение Пуассона и алгебраическая теория чисел.
23. Об оптимальном восстановлении решений классических уравнений математической физики
(Тезисы докладов 1-Съезда математиков Казахстана (11-14 сентября 1996 г.), Шымкент, 1996,
стр. 151-152)..……………………………………………………………………………………………………….…191
Первые результаты по теме «Компьютерного (вычислительного) поперечника», показывающие её содержательность.
24. Об эффективности алгоритмов численного интегрирования, связанных с теорией дивизоров в круговых полях
(Матем. заметки, 1997, №2, стр. 297-301)………………………………………………….……..………………….192
Efficiency of Numerical Integration Algorithms Related to Divisor Theory in Cyclotomic Fields (Mat. notes, 1997, Vol. 61, No 2, pp. 242-245)………………………………………………….………..196
Предложен способ построения квадратурных формул, основанный на теории дивизоров поля гауссовых чисел в круговых полях для функций производной и классов Никольского с доминирующей смешанной разностью.
25. О построении вероятностных мер на функциональных классах
(Труды Матем. инст. им. В.А.Стеклова РАН, 1997, т. 218, стр. 397-402)……………………………………..…...200
On the Construction of Probability Measures on Functional Classes
(Proceedings of the Steklov Institute of Mathematics, 1997, Vol. 218, pp.396-401)……………………………….....206
Представлен общий метод построения вероятностных мер на классах числовых последовательной. Даны их применения к классам Соболева, Никольского и Бесова.
26. Теоретико-числовые методы и теоретико-вероятностный подход к задачам Анализа. Теория вложений и приближений, абсолютная сходимость и преобразования рядов Фурье (Вестник Евразийского университета, 1997, №3, стр.90-144)…………………………………......……212
Реализация выдвинутой в статье «Қазаққа математика керек пе?» идеи (подробности во Введении), выполненной по результатам исследований нашей научной школы до 1997 года включительно (стр.5-210 настоящего сборника).
27. Классы
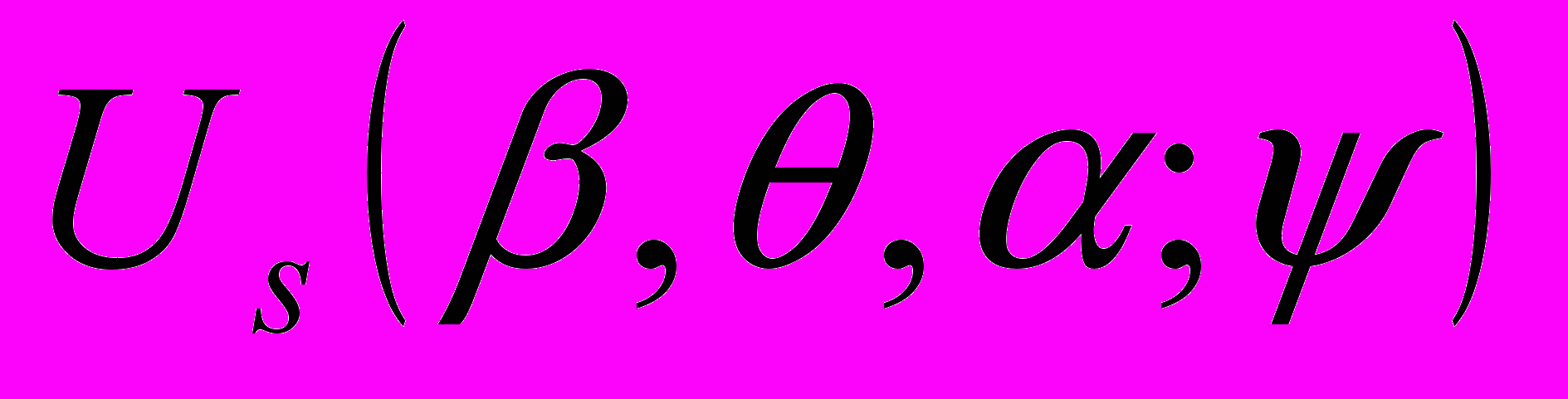и квадратурные формулы (Докл. РАН. 2003, т.393, №5, стр. 605-608.)................................................................................................................263
Classes
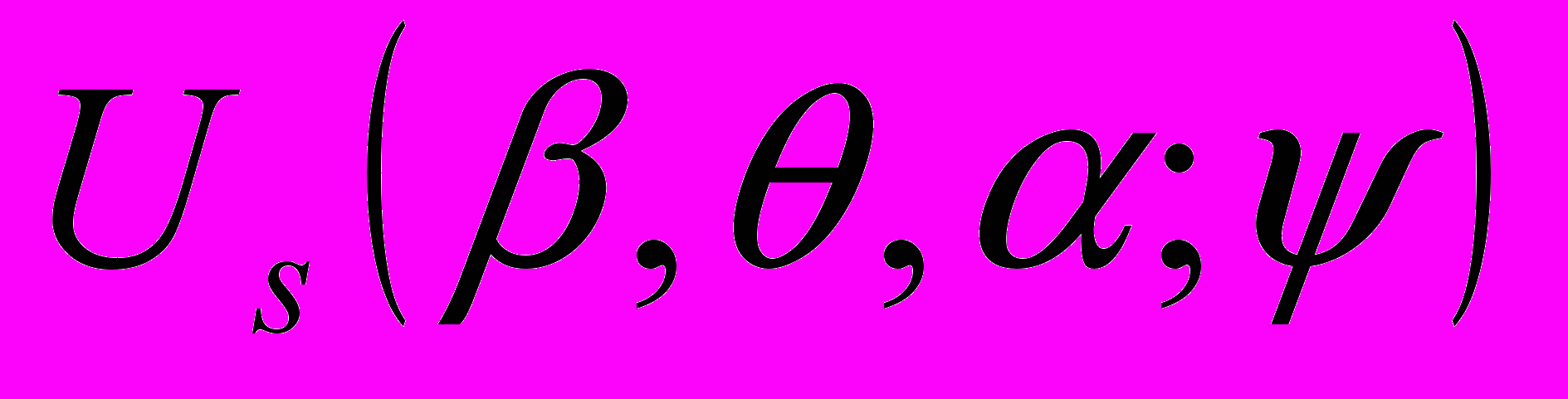and quadrature formulas (Dockland mathematics 2003,vol.68, no.3, pp.414-415). ............................................................................................. 267
На основе результатов П. Л. Ульянова (1990г.) определены новые классы функций, представляющие классификацию функций в широком диапазоне от предельно малой гладкости через известные классы Коробова до аналитических и их подклассов.
В качестве применения новой шкалы классов даны оценки погрешностей в них квадратурных формул Смоляка, полученных применением тензорных произведений функционалов.
28. Об информативной мощности линейных функционалов
(Матем. заметки, 2003, т.3, №.6, стр. 803-812. (совм. с Ш.Ажгалиевым))………………… ……………….....…271
Informativeness of Linear Functionals
(Mathematical Notes, Vol. 73, No 6, 2003, pp. 759-768.)………………………………….……………………….....281
Показана действенность нового понятия «Информативной мощности данного набора функционалов» в случае всех возможных линейных функционалов в задаче восстановления функций из классов Соболева, Никольского и Бесова.
29. Тензорные произведения функционалов и их применения к задачам восстановления (Вестник Евразийского национального университета, 2003, №4, стр. 67-73)…….…………….………………....291
От тензорных произведений классов функций С.А.Смоляка (1962 г.) к тензорным произведениям функционалов.
30. О задаче восстановления по неточной информации
(Вестник Евразийского национального университета, 2004, №1, стр. 202-209)…..…………………… ………..298
31. Предельная нечувствительность операторов восстановления по неточной информации (Тезисы докладов 10-ой Межвузовской конференции по математике и механике: Алматы, ЭВЕРО, т. 29, 2004, стр. 252-253)…………………………………………………………………...………………..307
Завершающий этап развития определения «Компьютерного (вычислительного) поперечника» в [30] и [31].
32. О дискретизации решений уравнения Пуассона
(Журнал вычислительной математики и математической физики, 2006, т. 46, №9, стр. 1594-1604 (совм. с Е.А.Баиловым)).……………………………………………………………………………………………………..…309
Discretization of the solutions to Poisson's equation
(Computational mathematics and mathematical physics, Vol. 46, No. 9, 2006, pp. 1515-1525 )…………..…………320
Берется результат из знаменитой монографии профессора МГУ Н.М. Коробова «Теоретико - числовые методы в приближенном анализе», опубликованной в 1963 году в серии «Библиотека прикладного анализа и вычислительной математики» и улучшается «в квадрат раз» (это же самое, если вместо затрат в $1000000 ту же работу выполнили за $1000) и на языке Компьютерного (вычислительного) поперечника» показываем, что дальше улучшить полученное нельзя.
33. О вложении классов
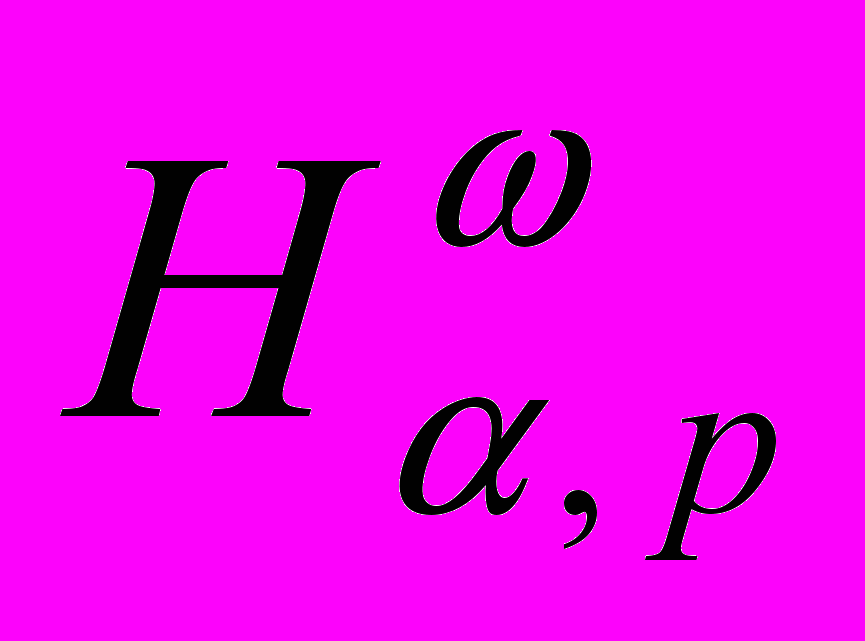в пространства Лоренца(Analysis Mathematica, 32, 2006, стр. 283-317 (совм. с. К.М.Сулейменовым))………………………………..….331
Американские математики Дитциан и Тотик ввели новый параметр в старое определение (модуля непрерывности).
В известном международном журнале (советско – венгерском, теперь российско – венгерском) «Analysis mathematicа» было исследовано влияние этого параметра. Статья оказалось с ошибками, что в международных журналах бывает крайне редко, да ещё и неокончательной.
Мы исправляем ошибки, решение задачи доводим до окончательного. Тем самым показываем, что в Астане критически читаем научные статьи и правильное решение публикуем в том же журнале на 35 страницах текста.
34. Информативная мощность всех линейных функционалов при восстановлении функций из классов
(Матем. сб., 2007,т. 198, №11, стр. 3-20 (совм. с Ш.Ажгалиевым))…..…….……………………..….…..………365
Informativeness of all the Linear Functionals in the recovery of functions in the classes
(Mathematical sb., 2007, pp.1535-1551)…………………...………………..……………..……………………….…..383
В математике объект, описывающий что-то реальное, понимается как сложный и его с заданной точностью заменяют в том или ином смысле простым.
В зависимости от поставленных целей такие задачи образуют разделы математики, именуемые «Численный анализ» и «Теория приближений», к основным понятиям которых относится, в частности, понятие «поперечника».
Разные поперечники решают разные задачи, мы предложили «Компьютерный (вычислительный) поперечник», нацеленный на отыскание наилучших вычислительных агрегатов для реализации на компьютерах.
Долго, порядка десяти лет, в математическом мире наши идеи, как и все новое, воспринималось с настороженностью, но указанные публикации в разных ведущих журналах есть свидетельство того, что признание пришло и мы на правильном пути ( как нам сказал один профессор МГУ «Верной дорогой идете, товарищи!»).
35. Об общем алгоритме численного интегрирования периодических функций многих переменных (Докл. РАН, 2007, т. 416, №2, стр. 169-173 (совм. с Е. А. Баиловым и А.Ж. Жубанышевой))....400
General algorithm for the numerical integration of Periodic function of several variables
(Dockland Mathematics, 2007, pp. 681-685)……………………………………………… …………………………..405
Ю. И. Манин: «К основным математическим моделям относится понятие интеграла – одна из центральных и постоянно повторяющихся тем в истории математики за последние два тысячалетия». При выполнении Проекта «Манхеттен» по созданию атомной бомбы в США возникла проблема вычисления интегралов высокой кратности и построения равномерно распределенных сеток (впоследствии оформленного в «метод Монте-Карло»), занимался Иохим фон Нейман.
То же повторилось при создании китайского ядерного оружия, занимались Вице-президент АН КНР Хуа Ло-Кен и академик АН КНР Вань Юань.
В СССР исследования проводились в научной школе Н.М.Коробова, по-видимому, самой успешной как в теоретическом, так и в вычислительном аспектах.
И так можно продолжить, например, большое количество статей выдающегося математика Эдмунда Хлавки и его школы (Австрия, ФРГ).
И все – же, несмотря на тысячи и тысячи статей и десятки монографий проблема решена не была, так в американском журнале «Contemporary Mathematics» Вань Юань писал (1988 год):
«По-видимому, одной из центральных проблем в численном интегрировании является нахождение прямых методов для получения оптимальных коэффициентов».
В статье [22] мы даем полное теоретическое решение, а в [24] – вычислительные результаты. В последнее время этот раздел математики называют «Научные вычисления».
Для сравнения: вычислительные результаты знаменитой школы Н.М.Коробова, опубликованные в знаменитом Институте общей физики АН СССР (1990 г.) мы существенно улучшаем в [24]: миллион точек и точность 10-12 школы Коробова мы снижаем до полумиллиона точек, одновременно повышая точность до 10-13 (для ориентировки 10-9 метра есть нанометр).
Теперь по всему миру ищем опубликованные таблицы вычислений, чтобы проверить мощь нашего метода – сидим в Астане и уверены, что в том же смысле улучшим.
36. Теоретико-числовые методы и теоретико-вероятностный подход к задачам Анализа. Теория вложений и приближений, абсолютная сходимость и преобразования рядов Фурье (Продолжение 1)(Вестник ЕНУ, 2002, №3-4, стр.222-272)…………………………………….….....410
Подготовлен к 75-летию выдающегося аналитика академика РАН П.Л.Ульянова (3.V.1928-13.XI.2006).
37. ПРОБЛЕМЫ ТЕОРИИ ФУНКЦИЙ И ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ (доклад, представленный на Всемирном Конгрессе математиков 2006 года в Мадриде)
(Вестник Евразийского национального университета, 2007, №2, стр. 19-51)………………….............................426
Развернутое изложение на родине, как это принято, 40-минутного одноименного доклада на Всемирном Конгрессе математиков 2006 года в Мадриде.
38. Об информативной мощности всех возможных линейных функционалов при дискретизации решений уравнения Клейна-Гордона в метрике
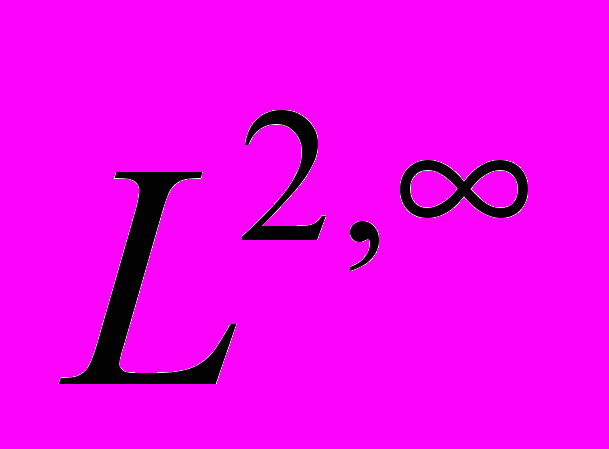
(Дифференциальные уравнения, 2008, т. 44, № 4, стр. 491-506 (совм. с И.Ж. Ибатулиным))……….…..………459
On the informative power of all possible linear functionals for the discretithation of the solutions of the Klein-Gordon equation in the metric of L2,
(Differential equation, vol.44, No.4, 2008, pp. 510-526)…………………………………….………………………...480
39. Применение теории дивизоров к построению таблиц оптимальных коэффициентов квадратурных формул
(Журнал вычислительной математики и математической физики, 2009, т.49, №1, стр. 14-25 (совм. с А.Ж.Жубанышевой и Ж.Н.Темиргалиевой))…………………………………………………………………….…..497
Application of divisor theory to the construction of tables of optimal coefficients for quadrature formulas
(Computational mathematics and mathematical physics, 2009, Vol. 49, No1, pp. 12-22).............................................509
Практический оптимальный алгоритм из [35], когда
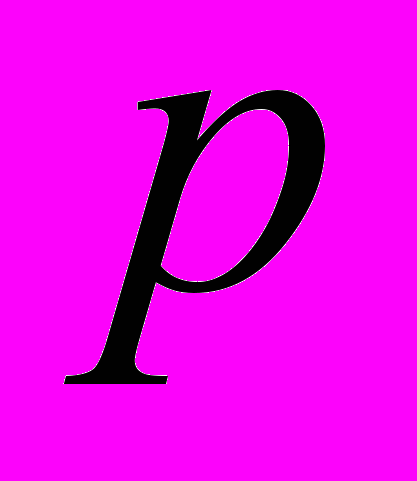узлов находятся за 
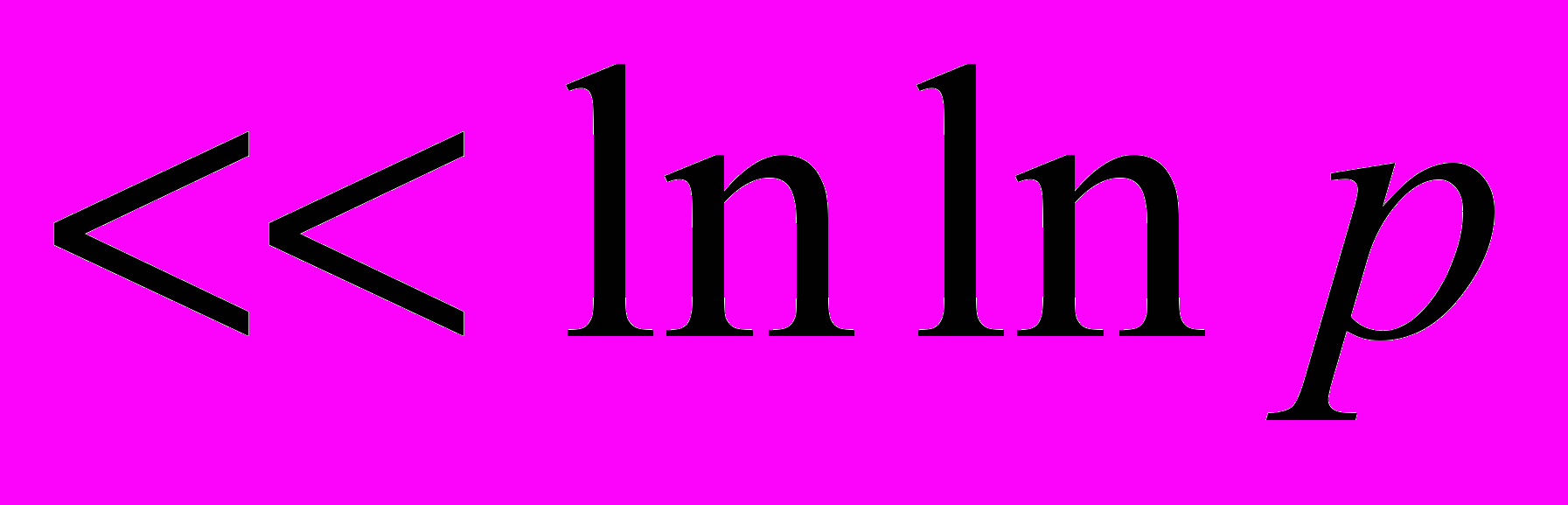элементарных арифметических операций при больших размерностях не поддается компьютерной реализации. В статье предложен и реализован метод вычислительных экспериментов нахождения оптимальных коэффициентов.40. Применение тензорных произведений функционалов в задачах численного интегрирования
(Изв. РАН, сер. матем., 2009, т. 73, №2, стр. 183-224 (совм. c C.С.Кудайбергеновым и А.А.Шомановой))…………………………………………………………………………………………………..….519
An application of tensor products of functionals in problems of numerical integration
(Izvestiya: Mathematics, 2009, Vol. 73, No 2, pp. 393-434)…………………………………………………….…… 560
41. О порядке дискрепанса сетки Смоляка
(Матем. заметки, 2009, т. 85, № 6, 947-950 (совм. c Н.Ж.Наурызбаевым ))………………………….…………..602
Оn the Order of Discrepancy of the Smolyak Grid
(Mathematical Notes, 2009, Vol. 85, No 6, pp. 897-901)………..………………..……………………………………606
В 1963 году в Докл. АН СССР была опубликована статья, повлекшая много публикаций; эта тема на Западе именуется как «Метод Смоляка». Нами был вскрыт механизм действия этого метода и на 42 страницах текста дано полное исследование одной самой популярной его реализации в виде квадратурной формулы.
Публикация [41] о очень плохом распределении сетки Смоляка, вместе с [40] закрывает эту тему.
42. Тензорные произведения функционалов и их применения
(Докл.РАН, 2010, т. 430, № 4, с. 460-465.)………………………………………………………………..611
Tensor Products of Functionals and Their Application
(Docklandy Mathematics, 2010, Vol. 81, No.1, pp. 78-82….………..……………………………………617
Введено новое понятие «Тензорные произведения функционалов», на основе которой получены новые квадратурные формулы и операторы восстановления. Показаны их вычислительные применения в соответствии с результатами из [39].
43. Применения квадратурных формул Смоляка к численному интегрированию коэффициентов Фурье и в задачах восстановления
(Изв. ВУЗов. Математика. 2010, №3. С.52-71.)……………………………………………………...…..622
Applications of Smolyak quadrature formulas to the numerical integration of Fourier coefficients and in function recovery problems
(Russian Mathematics (Iz VUZ) 54:3 (2010), 45-62 (совм. с C.С.Кудайбергеновым, А.А.Шомановой))...606
Получены точные порядки численного интегрирования коэффициентов Фурье и показаны их применения в задачах восстановления.
44. О точном порядке информативной мощности всех возможных линейных функционалов при дискретизации решений волнового уравнения
(Дифф. уравн., т. 46, № 8, 2010, стр. 1201-1204(совм. с Ш.К.Абикеновой))……………………..602
On the sharp order of informativeness all posibble linear functionals in the discretization of solutions of the wave equation
(Differential equations, 2010, V. 46, №8, pp.1201-1204)….………………………………..……………641
Найдены точные порядки дискретизации в Lq - метрике решений уравнения теплопроводности с начальными условиями из классов Соболева вычислительными агрегатами, построенных по информации, полученных от всех возможных линейных функционалов.
45. Об алгоритме построения равномерно распределенных сеток Коробова // Матем. замет., 2010, том 87, №6 стр.948-950 (совм. с. М. Сиховым)
On an algorithm for construction uniformly distribution Korobov grids // Mathematical notes, 2010, vol. 87, No. 6, pp. 916-917.
Дополнение
Статьи, выполненные при консультативном участии Н. Темиргалиева
- Алшынбаева Е. О преобразованиях коэффициентов Фурье некоторых классов функций //Докл. АН СССР.1977. Т.236, №6.С. 1293-1295.
- Алшынбаева Е. О преобразованиях коэффициентов Фурье некоторых классов функций //Матем. заметки.1979.Т.25,№5.С.645-651.
Получен критерий замкнутости пространств Орлича относительно преобразований Харди и Беллмана тригонометрических рядов Фурье – сама и дополнительная
функция в определении пространств Орлича должны удовлетворять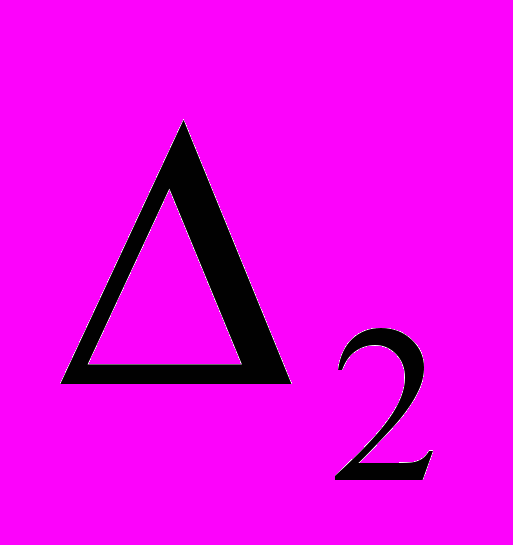 
- условию соответственно.- Джумакаева Г.Т. Критерий вложения класса Соболева - Морри
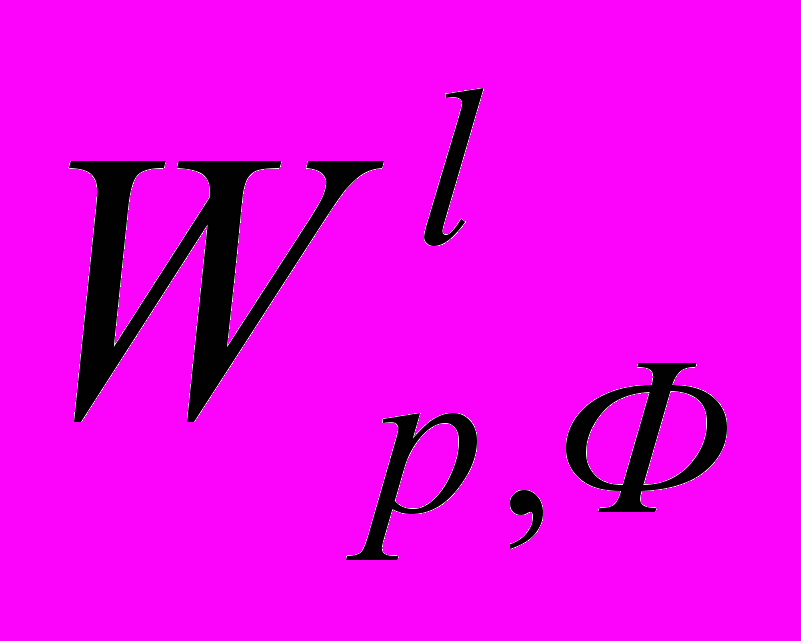в пространство С // Матем. заметки. 1985.Т. 37, № 3.С. 399-406.
Иллюстративный результат по теме «Морри», в свое время, в бытность Главным редактором С.Б.Стечкина, получивший из «Математических заметок» денежную премию как перспективная статья (в то время как известный математик по теме дал отрицательный отзыв).
- Сихов М.Б. О прямых и обратных теоремах теории приближений с заданной мажорантой // Analysis Mathematica. V.30. №2. 2004. С. 137-146.
Впервые получен, по-видимому, точный порядок «Предпоперечника Колмогорова».
- Нурмолдин Е.Е. Восстановление функций, интегралов и решений уравнения теплопроводности из
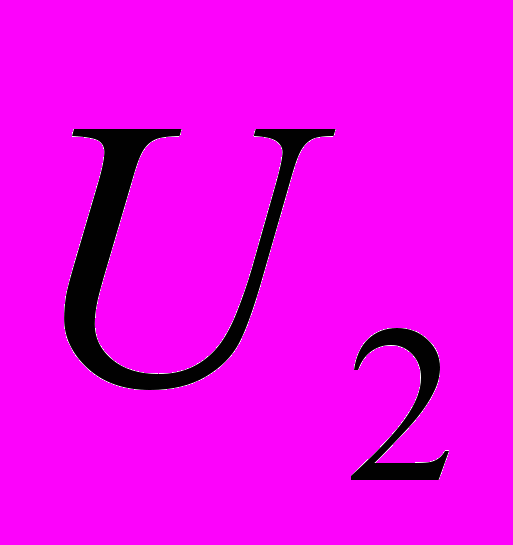классов Ульянова // Сиб. журн. вычисл. математики, 2005. – Т.8, №4. – С. 337-351.
Определение нового класса Ульянова привело к новому по звучанию результату.
- Ковалева И.М. Восстановление и интегрирование функций из анизотропного класса Коробова // Сибирский журнал вычислительной математики. Т. 5. № 3. С. 255-266.
Теоремы существования из знаменитой монографии снабжены эффективными алгоритмами.
- Жайнибекова М.А. О соотношениях между модулями непрерывности и наилучшими приближениями в разных метриках и некоторые многомерные теоремы вложения. Кандидатская диссертация. КазГУ. Алматы.1985. Фрагмент кандидатской диссертации (Об одной теореме вложения, Ред.ж. «Вестник АН Каз.ССР», Деп. в ВИНИТ И 22 ноября 1984 г. № 7476-84 ДЕП., 31с.)
- Сихов М.Б. О некоторых соотношениях между модулями гладкости и наилучшими приближениями тригонометрическими полиномами в разных метриках. Кандидатская диссертация. КазГУ. Алматы.1988. Фрагмент кандидатской диссертации.
В дополнение к соотношению Потапова – Симонова (в одной и той же метрике
, 
; 
) 
(
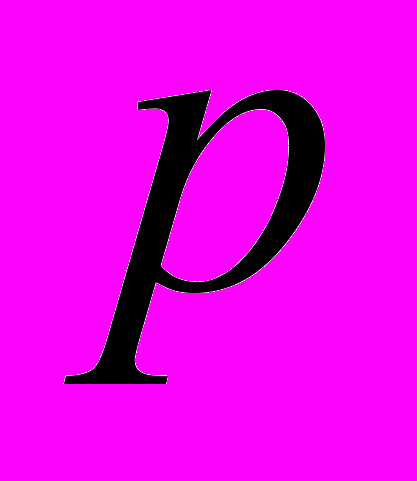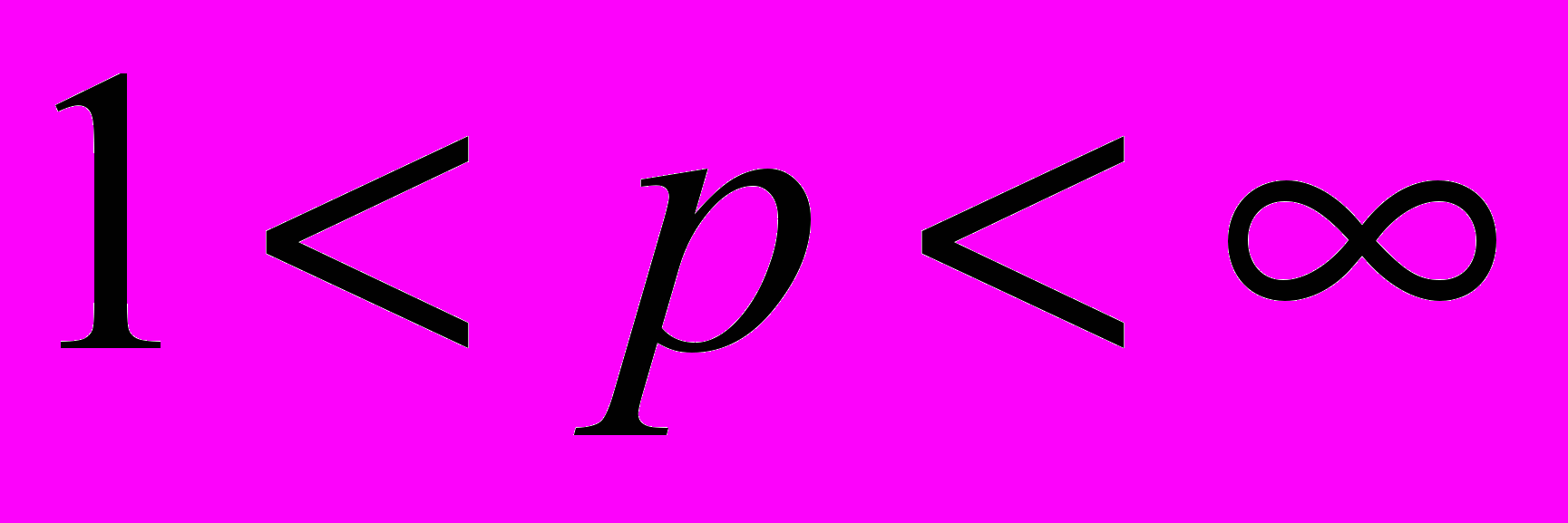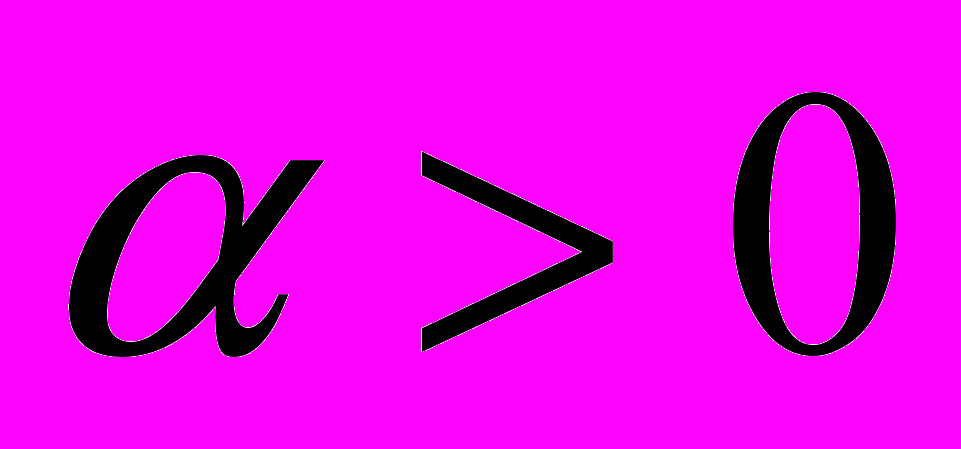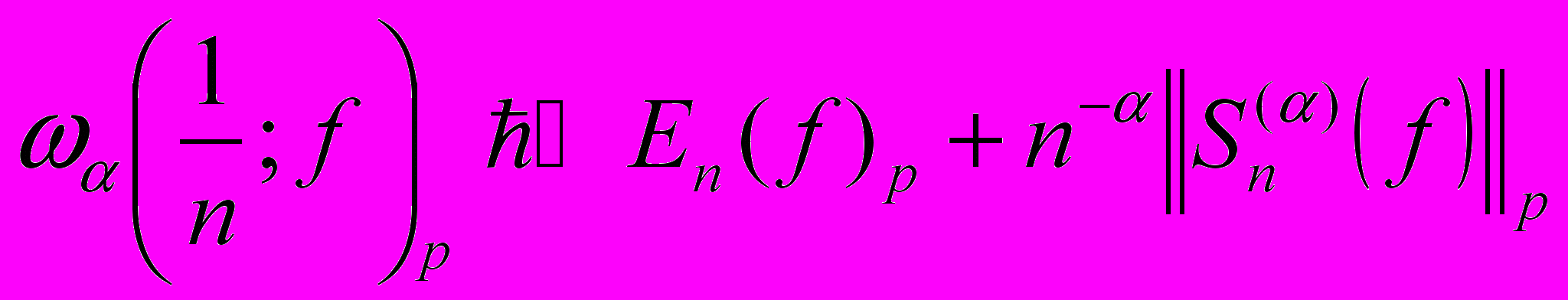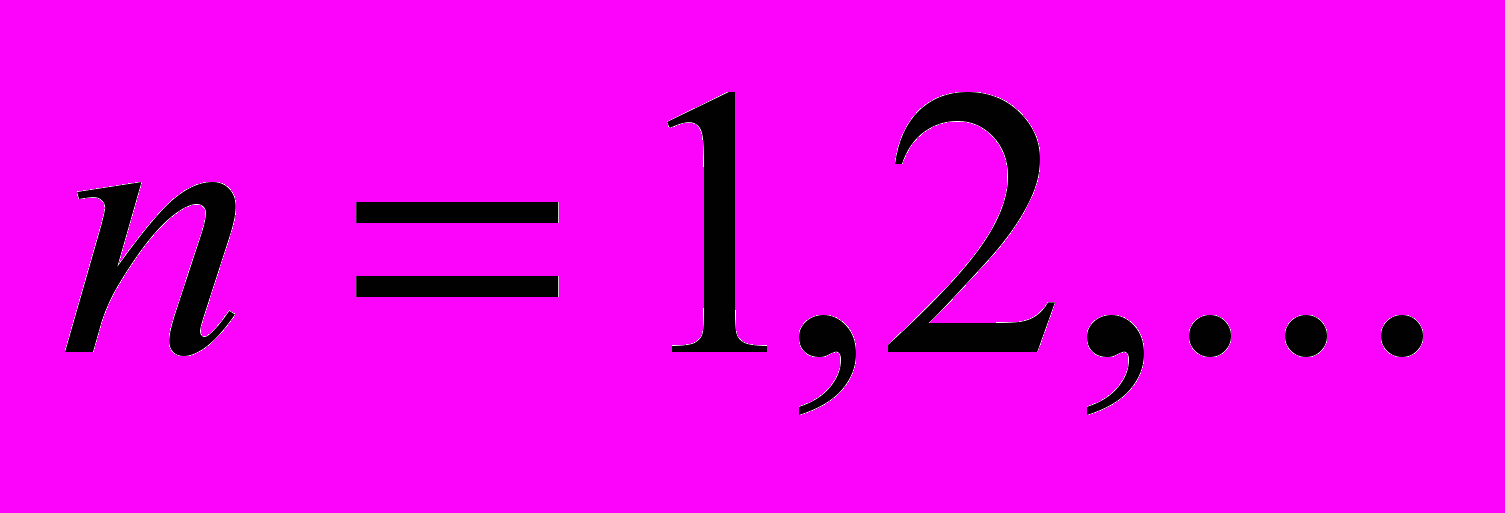) , из которых при
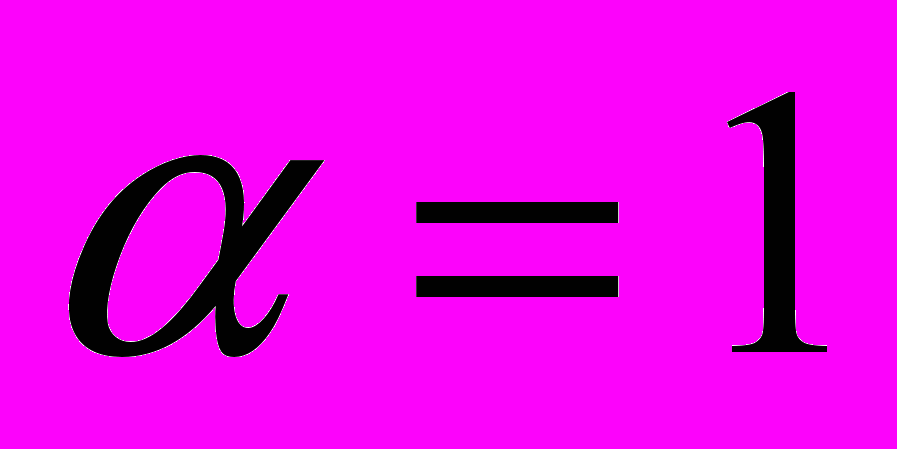следуют существенные улучшения и уточнения неравенств Джексона и Бернштейна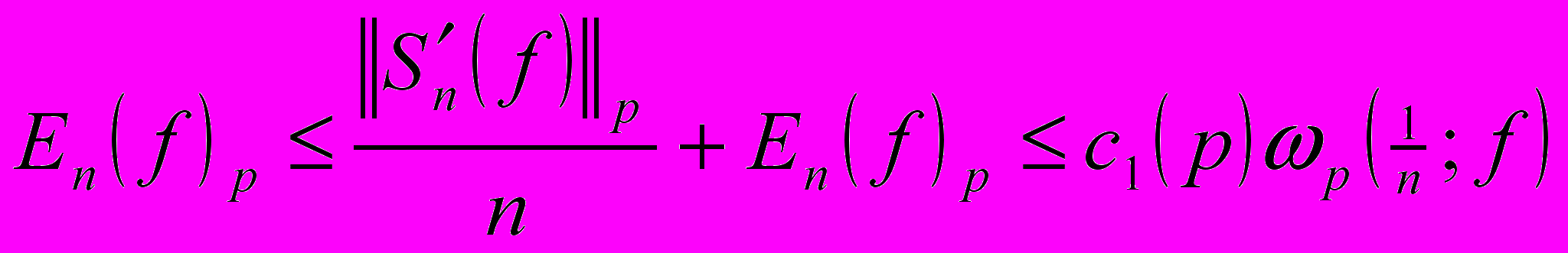 
и
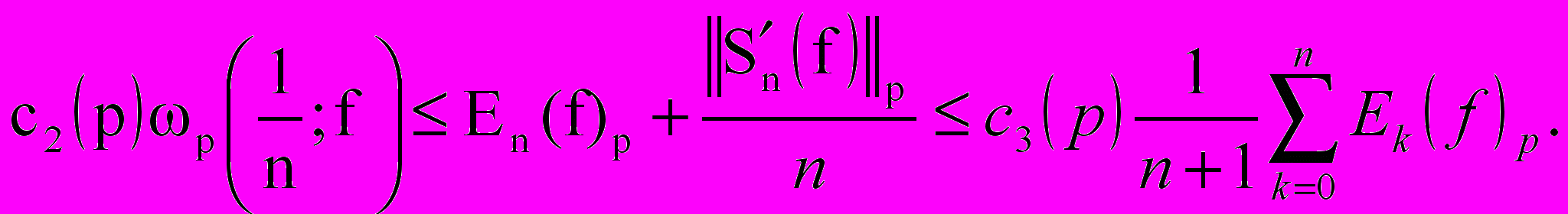
соответственно, в случае разных метрик неусиляемые теоремы получены М. Жайнибековой и М.Сиховым
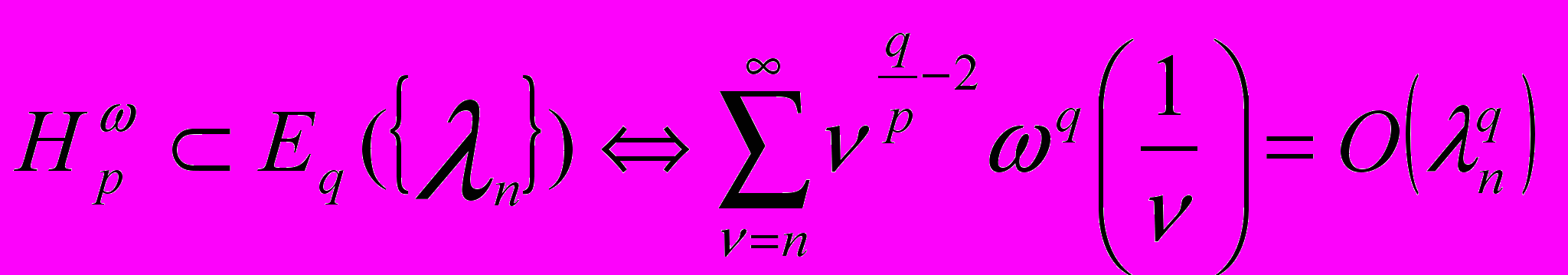,и
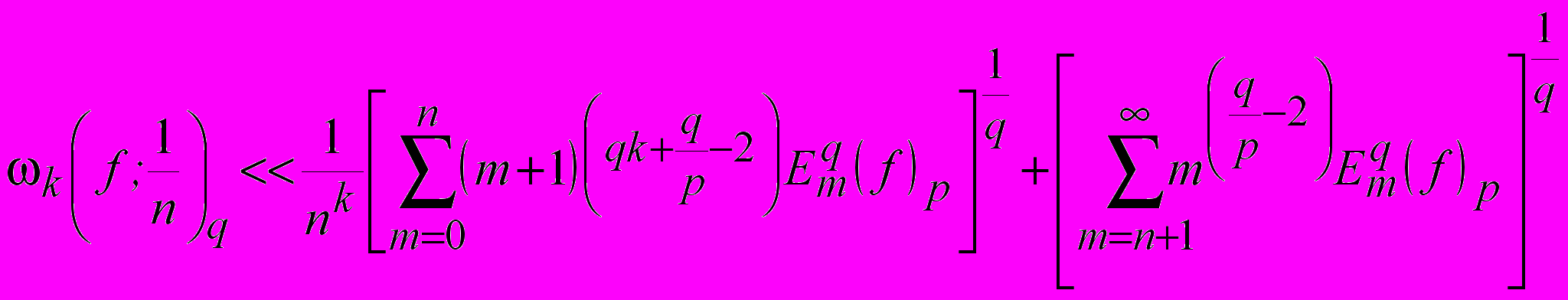
- прямые и обратные теоремы теории приближений в разных метриках соответственно.
- Даркенбаев С.З. О сходимости рядов из тригонометрических коэффициентов Фурье //Изв. АН Каз.ССР. Сер. физ.-мат.1985.№5.С.22-27.
- Даркенбаев С.З. О сходимости рядов из коэффициентов Фурье по мультипликативным системам // Изв. АН КазССР. Сер. физ.-мат.1990. №5.С.14-17.
В теме абсолютной сходимости тригонометрических рядов Фурье, где классические результаты принадлежат С.Н. Бернштейну и С.Б. Стечкину, в дополнение найден неисследованный случай с новым логарифмическим эффектом (впервые в случае теории вложений установленный – Н.Темиргалиевым, в случае «Морри» - К.Ж. Наурызбаевым и Г.Т. Джумакаевой).