Математика: наука

Вид материала

Документы

Подобный материал:

• Колмогоров Андрей Николаевич, 563.58kb.
• Задачи и упражнения по математическому анализу для втузов. Под ред. Б. П. Демидовича., 19.39kb.
• Византийская математика, 186.7kb.
• «Математика. Прикладная математика», 366.03kb.
• Программа подраздела «Философские проблемы математики», 94.9kb.
• Расшифровка : Математика, 146.94kb.
• Что такое прикладная математика?, 81.59kb.
• Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
• Пангеометризм и математическая мифология, 956.71kb.
• Программа Фестиваля Мероприятия мгу им. М. В. Ломоносова, 971.43kb.

§1. Компьютерный (вычислительный) поперечник…...…………….………..………………12

1. Введение………………………………………………………………………………………….12

2. Поперечники как формулировки разных оптимизационных задач теории приближений (аппроксимаций)………………………………………………..…………………………………...18

3. Идея Компьютерного (вычислительного) поперечника………...…………………………....18
   
4. Определение Компьютерного (вычислительного) поперечника по точной информации…………………………………………………...……………………………………..19
   
5. Важнейшие примеры функционалов 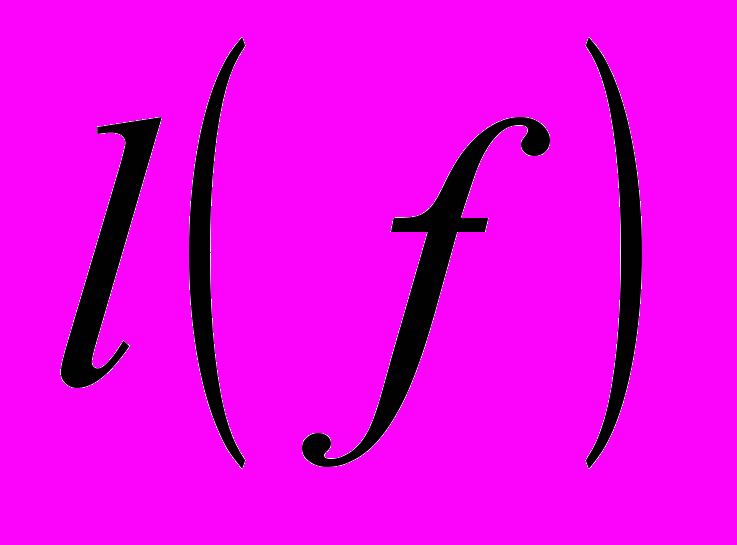и операторов 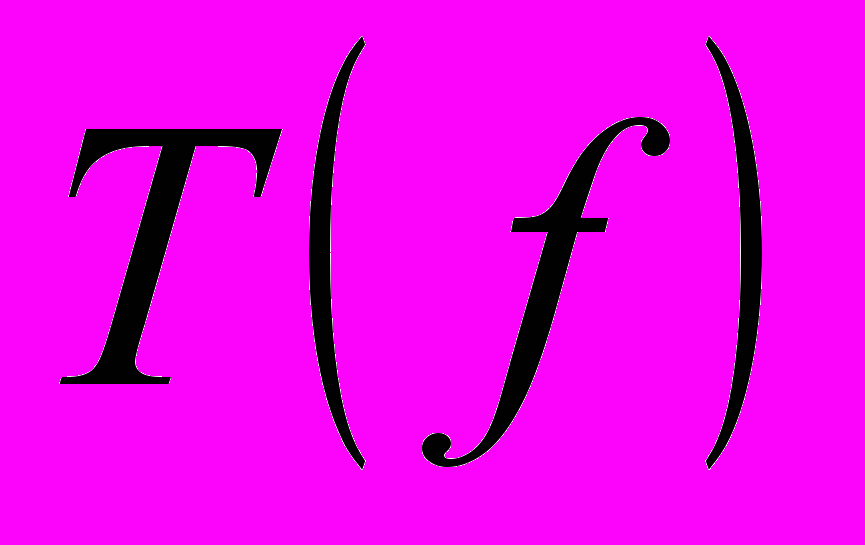в определении Компьютерного (вычислительного) поперечника…………...……………………………………21
   
6. О структуре наборов вычислительных агрегатов D_N в определении Компьютерного (вычислительного) поперечника……………………………...……………………………………23
   
7. Поперечник Колмогорова……………………………………...……………………………….23
   
8. Аппроксимативные возможности множества всех полиномов по данной системе линейно независимых функций (Предпоперечник Колмогорова)……………………..…………………..24
   
9. Вычислительные агрегаты, построенные по линейным функционалам и линейным алгоритмам…………………………………………………………………………………………...25
   
10. Пример поперечника, не вписывающегося в схему Компьютерного (вычислительного) поперечника……………………………………………………………...…………………………..29
    
11. Общее определение Компьютерного (вычислительного) поперечника…………...………...32
    
12. Заключительные замечания к определению Компьютерного (вычислительного) поперечника…………………………………………………………………………...……………..33
    
13. Иллюстративные результаты по теме Компьютерного (вычислительного) поперечника (по точной информации)…………………………………………………………..…………………….35
    
14. Иллюстративные результаты по теме Компьютерного (вычислительного) поперечника - предельная погрешность неточной информации при оптимальном восстановлении……….…37
    
15. Эффективизация поперечников…………………………………………….…..……………....40
    
16. Постановка задачи восстановления типа «информационного шума» (noisy information)…………………………………………………………………………………………...41
    
17. Точные результаты по неточной информации (В.М.Тихомиров, Г.Г.Магарил – Ильяев, К.Ю. Осипенко, А.Г.Марчук)…………………………………………...………………………….44
    
18. Задачи……………………………………………………………………...……………………..48
    

§2. Классы функций…………..…………………………………………………..………………..53

1. Классы функций как важнейшая составляющая постановки задач в непрерывной математике……………………………………………...……………………………………………53

2. Классы Лебега и Орлича……………………………...………………………………………...53
   
3. Классы Соболева, Никольского и Бесова W, H и B (см. напр., [1], стр.48,59 и 66-
   

67, соответственно)………………………………………...……………………………………54

4. Классы функций с доминирующей смешанной производной……………………………..…56
   
5. Классы Ульянова 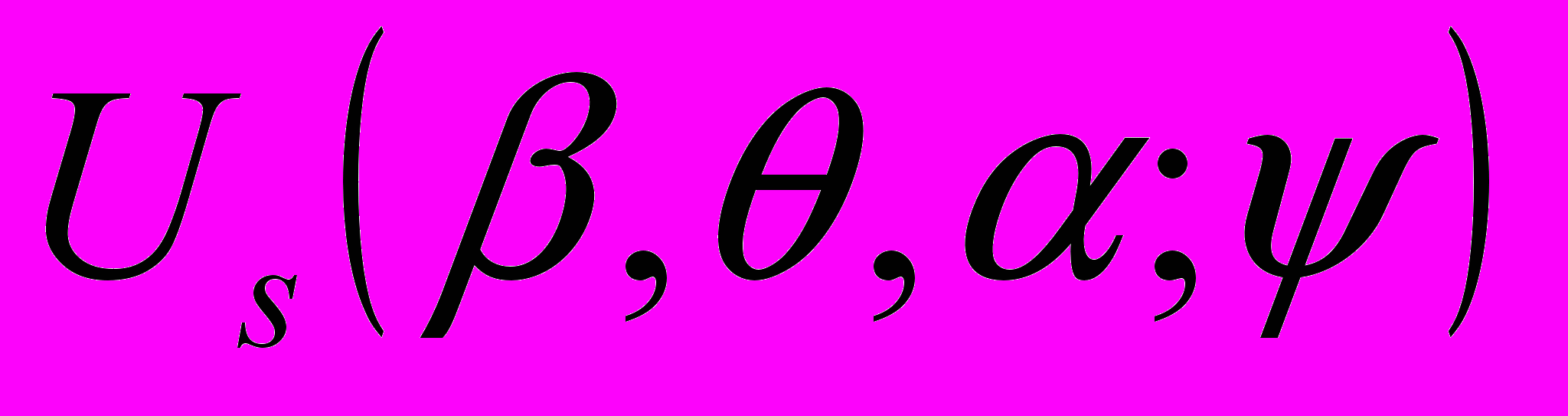(см. [6])………………...……………………………………57
   
6. Функциональные классы 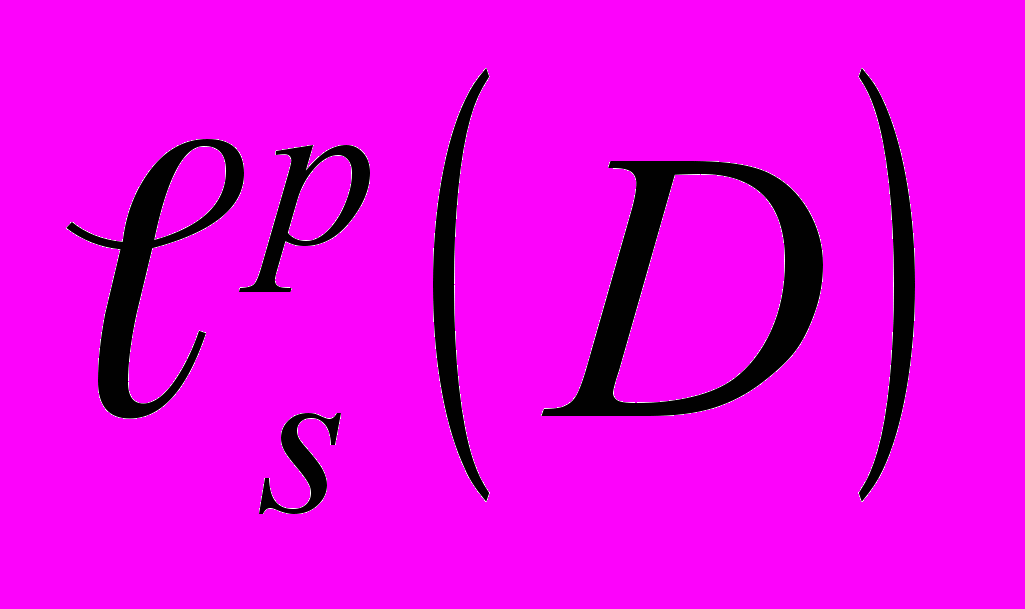(см. [8])………………………………………………………59
   
7. Весовые классы Коробова (см. [10])………………………………...…………………………60
   
8. Функциональные классы 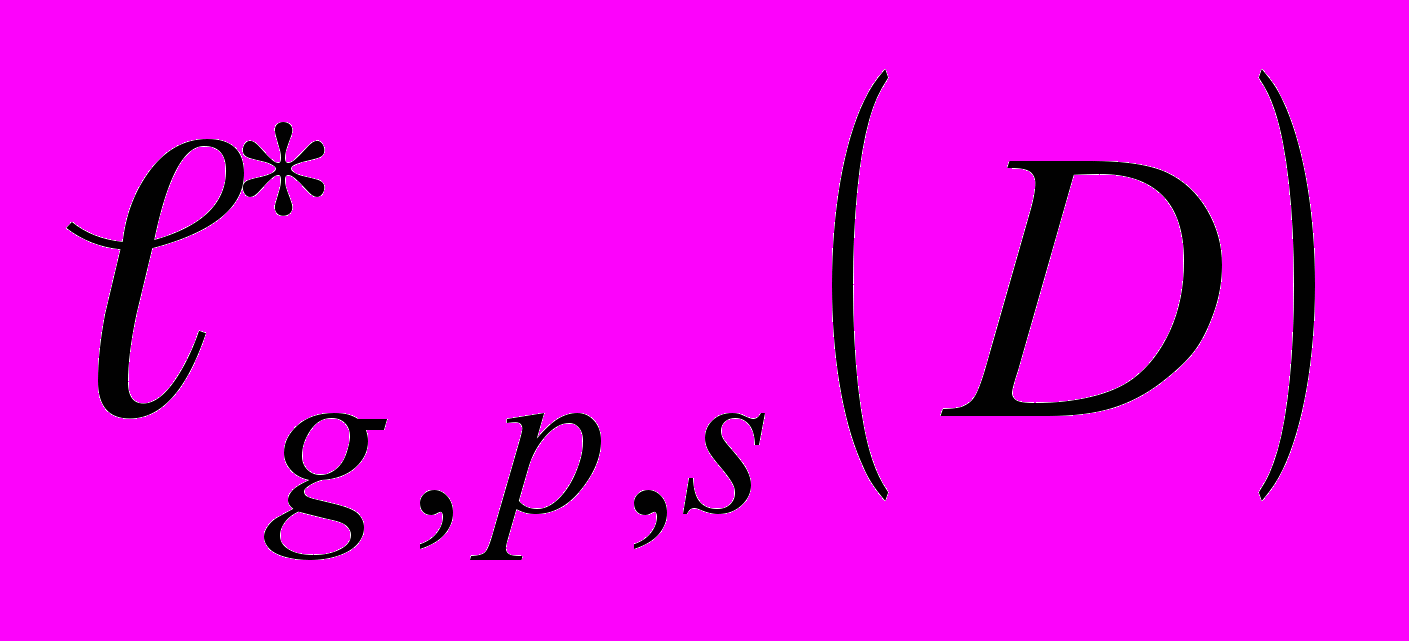(см. [8])……………………………………………………60
   
9. Обобщенные классы Мори…………………………………………………………………...…62
   
10. Класс (см [18]).......................................................................................................................65
    

§3. Алгебраическая теория чисел и тензорные произведения функционалов (в сочетании с гармоническим анализом) в задачах восстановления…………………..………........…..68

1. Идея применения алгебраической теории чисел в задачах алгебры, геометрии
   

чисел и анализа..............................................................................................................................68

2. Тензорные произведения функционалов……………………………...……………………….69
   
3. Квадратурные формулы Смоляка………………………………………………………………71
   

§4. Равномерно распределенные сетки и задача эффективизации метода Монте-Карло..73

1. Равномерно распределенные сетки Коробова…………………………………………………74
   
2. Задача построения равномерно распределенных сеток Коробова (эффективизация
   

метода Монте-Карло)…………………………………………………………………………....75

3. Необходимые сведения из алгебраической теории чисел…………………………………….77
   
4. Метод сравнений в задаче построения равномерно распределенных сеток……...…………79
   
5. Алгоритм построения равномерно распределенных сеток…………………………………...80
   
6. Алгоритм построения решетки, близкой к критической……………………...……………...81
   
7. Алгоритм построения равномерно распределенных сеток Коробова в случае
   

размерности пространства ………………………………………………………….……83