Математика: наука
| Вид материала | Документы |
- Колмогоров Андрей Николаевич, 563.58kb.
- Задачи и упражнения по математическому анализу для втузов. Под ред. Б. П. Демидовича., 19.39kb.
- Византийская математика, 186.7kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Расшифровка : Математика, 146.94kb.
- Что такое прикладная математика?, 81.59kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
- Программа Фестиваля Мероприятия мгу им. М. В. Ломоносова, 971.43kb.
§8. Дискретизация решений уравнений в частных производных……….……..…………..159
Введение……………………………………………………..……………………………………...159
- Дискретизация решений уравнения теплопроводности (теоремы К.Шерниязова,
Ш.Ажгалиева, Е.Нурмолдина)…………………………………………………………...……162
- Дискретизация решений волнового уравнения………………………………………………165
- Дискретизация решений уравнения Пуассона…………………………...…………………..168
- Дискретизация решений уравнения Клейна-Гордона…………...…………………………..171
- Дискретизация решений уравнения Лапласа…………...……………………………………173
- Информативная мощность всевозможных линейных функционалов при дискретизации решений задачи Дирихле для уравнения Лапласа…………….……..…………………………..174
- Дискретизация решений задачи Дирихле для уравнения Лапласа в бесконечной полосе и в прямоугольнике………………………………………………………………..…………………...175
§9. Теоретико-вероятностный подход к задачам Анализа…………………………………..179
- Теоретико-функциональный и теоретико-вероятностный подходы к задачам Анализа……………………………………………………………………………………...……...179
- Средние относительно вероятностных мер на функциональных классах погрешности операторов восстановления………………………………………………….…………………….180
- Средние погрешности метода интегрирования Монте-Карло………………………………180
- Построение вероятностных мер на классах функций………………...……………………..181
- Одно замечание относительно теоретико-функциональных и теоретико-вероятностных постановок задач……………………………………………………………...……………………184
- Средние погрешности детерминированных квадратурных формул………………………..185
- Средние погрешности методов интегрирования Монте-Карло………………...…………..186
- Дискретизация решений уравнений в частных производных в среднем………...………...187
- Поперечники в среднем……………………………………………………..………………..188
- Применение вероятностных мер к задаче вычисления экстремума функционала………...189
- Дискретизация в среднем квадратичном относительно вероятностных мер решений уравнения Клейна – Гордона……………………………………………………...……................190
- Средние квадратические погрешности дискретизации решений уравнения Лапласа……192
Перспективы…………………………………………………………………...………………...…194
§10. Теория вложений и приближений………………….…………………………..………...198
1. Прямые и обратные задачи теории приближений (в одной метрике)…………...…………..198
2. Теоремы вложения (вокруг подхода П.Л. Ульянова)………………………..………………199
3. Критерий вложения классов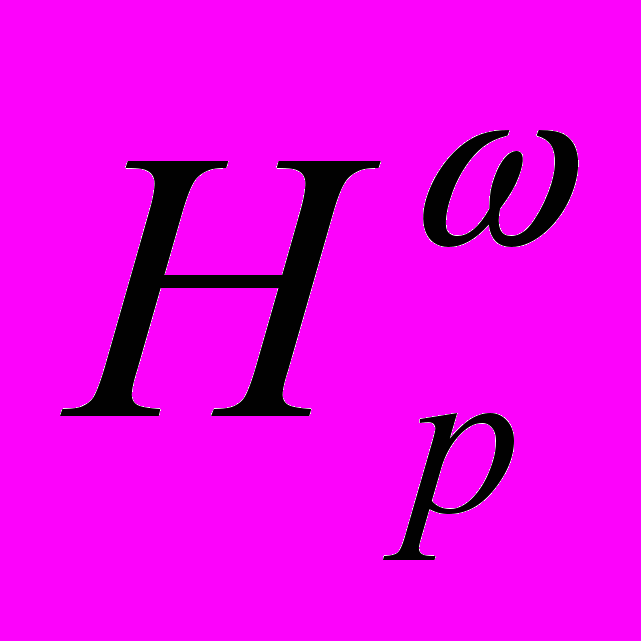 
в пространство Лоренца 
…………..……………..209
4. Методы гармонического анализа ………………………………………………..……………213
5. Прямые и обратные задачи теории приближений (в разных метриках)………..………..…214
6. Новые задачи об аппроксимативных возможностях полиномов по ортогональным системам с произвольным спектром ………………………………………………..……………………...217
7. Теорема М. Сихова об оптимальном приближении функций из классов в зависимости от спектра приближающих тригонометрических многочленов (с комментариями)………..…...218
8. Классы типа Морри (иллюстративный результат – теорема Г.Т.Джумакаевой о вложении классов Соболева-Морри в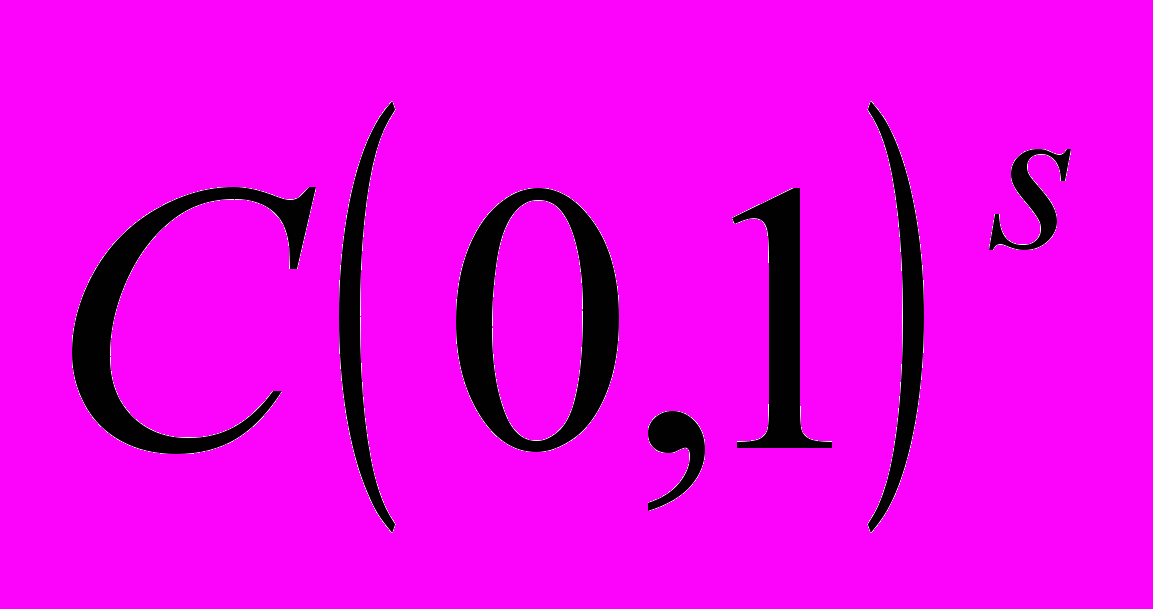 
)……………………………………………………….……...225
9. Модули непрерывности переменного приращения и теоремы вложения (К. Сулейменов, Н. Темиргалиев) ………………………………………………………………………………………228
§11. Ряды Фурье……………..…………………………………………………….……………...236
1. Преобразования коэффициентов рядов Фурье………………………………………………...236
2. Абсолютная сходимость рядов Фурье…………………………………...…………………….237
3. Критерии интегрируемости высших производных…………………………...………………239
4. Суммирование рядов Фурье…………………………………………………………………….240
КАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Л.Н. Гумилев атындағы Еуразия ұлттық университеті
Н. Темірғалиев
ТАҢДАМАЛЫ. ҒЫЛЫМ
Н. Темиргалиев
ИЗБРАННОЕ. НАУКА
N. Temirgaliyev
SELECTED PUBLICATIONS. SCIENCE
АСТАНА
2009
Предисловие
Евразийский национальный университет им. Л. Н. Гумилева принял решение об издании избранных научных трудов крупного казахского математика, профессора Нурлана Темиргалиева. Профессор Темиргалиев - сам возглавляющий сегодня научную школу, активно работающую в Казахстане – воспитанник московской школы метрической теории функций, созданной выдающимися русскими учеными Д.Е. Меньшовым и П.Л. Ульяновым. Для всех участников этой школы настоящее издание - знаменательное событие. Читатели получают возможность оценить итоги исследований, о которых Н. Темиргалиев рассказывал нам на протяжении более чем тридцати лет. И самое главное, что тематика этих исследований полностью сохраняет свою актуальность, а, значит, книга представляет интерес для широкого круга читателей. В статьях, включенных в настоящее издание, центральными являются две крупные темы:
Исследование классов функций многих переменных и, в частности, теорем вложения;
Квадратурные формулы, вопросы численного интегрирования и приближенного восстановления функций по дискретным данным.
Исследование теорем вложения для классов функций многих переменных было начато Н. Темиргалиевым в аспирантские годы, как продолжение исследований его учителя академика П.Л. Ульянова (1928-2006), посвященных классам функций одной переменной. Уже в работах основателей теории вложения функциональных классов С.Л. Соболева и С.М. Никольского было выяснено, что многомерный случай требует развития новых, по сравнению с одномерным случаем, методов, что проявилось и в исследованиях Н. Темиргалиева.
С середины 80-х годов прошлого века центральное направление в исследованиях Н.Темиргалиева - многомерные кубатурные формулы и вопросы восстановления функций многих переменных по дискретной информации. Первые работы по кубатурным формулам были выполнены Н.Темиргалиевым совместно с выдающимся специалистом по теории чисел профессором С.М.Ворониным (1946- 1997). В этой классической области анализа теоретико-числовые методы традиционно играют важную роль, поэтому не удивительно, что сотрудничество специалистов по теории чисел и теории функций оказалось весьма плодотворным. Под влиянием С.М.Воронина Нурлан Темиргалиев изучил и стал использовать теорию дивизоров в полях алгебраических чисел в качестве основного аппарата для эффективного построения оптимальных многомерных кубатурных формул. Эти исследования составили основу докторской диссертации «Об эффективности алгоритмов численного интегрирования и восстановления функций многих переменных», которую Н. Темиргалиев защитил в Математическом институте им. В.А.Стеклова АН СССР в 1991 г. В последующие годы теоретико-числовые и вероятностные методы исследований функций многих переменных активно развивались Н.Темиргалиевым и его учениками. Следует отметить, что это направление в анализе находит в последние годы все новые и новые приложения.
Надеюсь, что издание избранных трудов профессора Н.Темиргалиева даст новый импульс развитию исследований по математическому анализу.
Заведующий кафедрой теории функций
и функционального анализа Московского
государственного университета
им. М. В. Ломоносова, член- корреспондент РАН Б.С. Кашин
АННОТИРОВАННОЕ ОГЛАВЛЕНИЕ
Предисловие ………………………………………………………………………………………………….….……3
Слово об авторе ……………………………………………………………………………………………….…..….4
1. Некоторые теоремы вложения классов функций
многих переменных(Изв. АН КазССР, сер. физ.-матем., 1970, №5, стр. 90-92)………………………………………….….……..……....5
1968 году на Республиканскую межвузовскую конференцию (КазГУ: Ректор А.З.Закарин, Декан механико-математического факультета Х.И. Ибрашев) были приглашены молодые, но уже заявившие о себе в математике, ученые с целью установления, как говорят, «научных связей».
Среди них был и сорокалетний Ульянов Петр Лаврентьевич, который рассказал о, тогда еще неопубликованной, знаменитой теореме (
) 
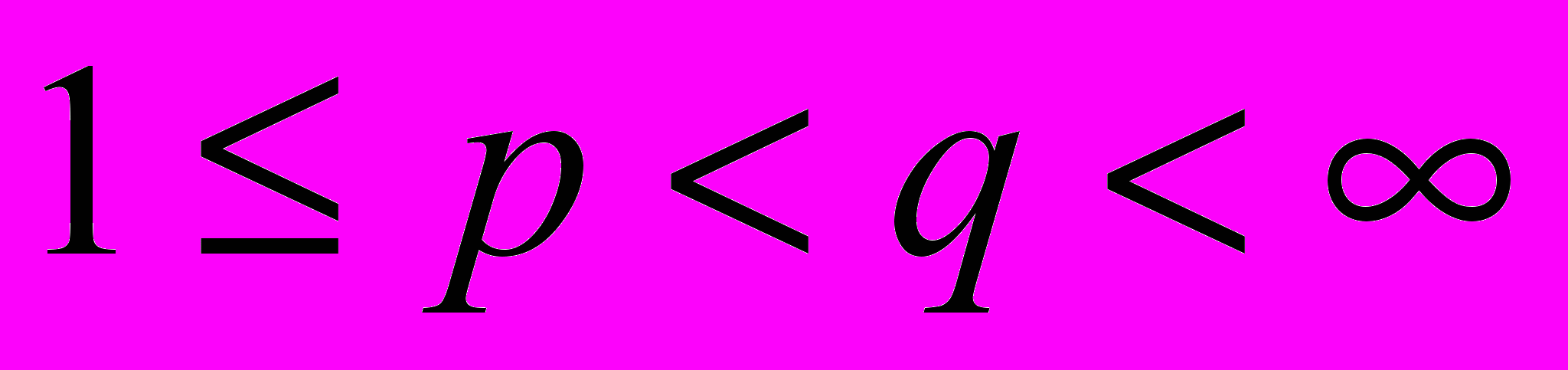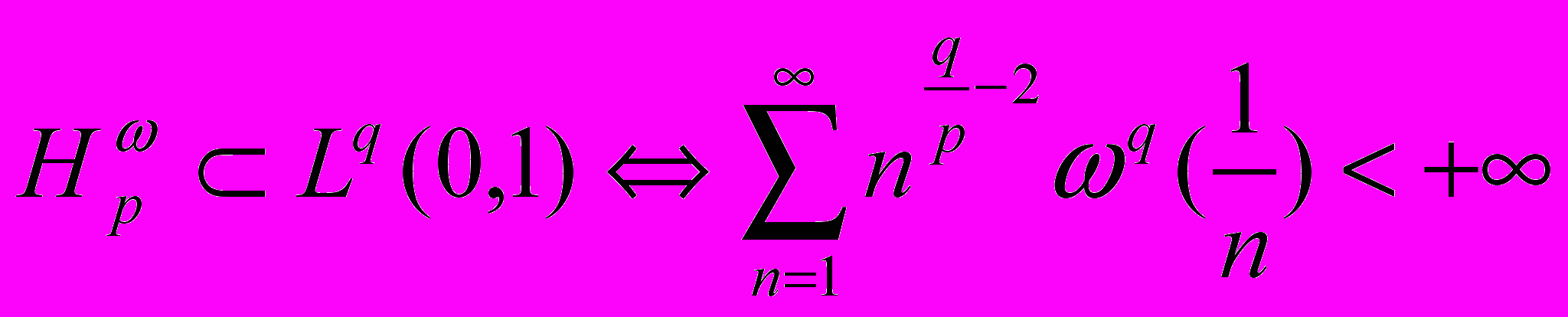.Наурызбаев Кабдуш Жумагазиевич, мой научный руководитель, запомнил что, как сказал П.Л.Ульянов, статья по его докладу выйдет в 1968 году в журнале Изв. АН СССР, серия матем., и дал мне задачу оттуда «… было бы небезынтересно изучить одномерные результаты также в случае многомерном» в качестве дипломной работы.
В этой статье опубликованы результаты этой дипломной работы, которые также в 1969 году привели меня в аспирантуру Математического института им В.А.Стеклова АН СССР.
2. О связи теорем вложения с равномерной сходимостью кратных рядов Фурье
(Матем. заметки, 1972, т. 12, №2, стр. 139-148)………………………………………………………….…….....……8
A connection between inclusion theorems and the uniform convergence of multiple
Fourier series (Mat. zametki,1972, pp.518-523)……………………………………………………………….… …18
Л. Ульяновым (1967) в одномерном случае было установлено, что вложение
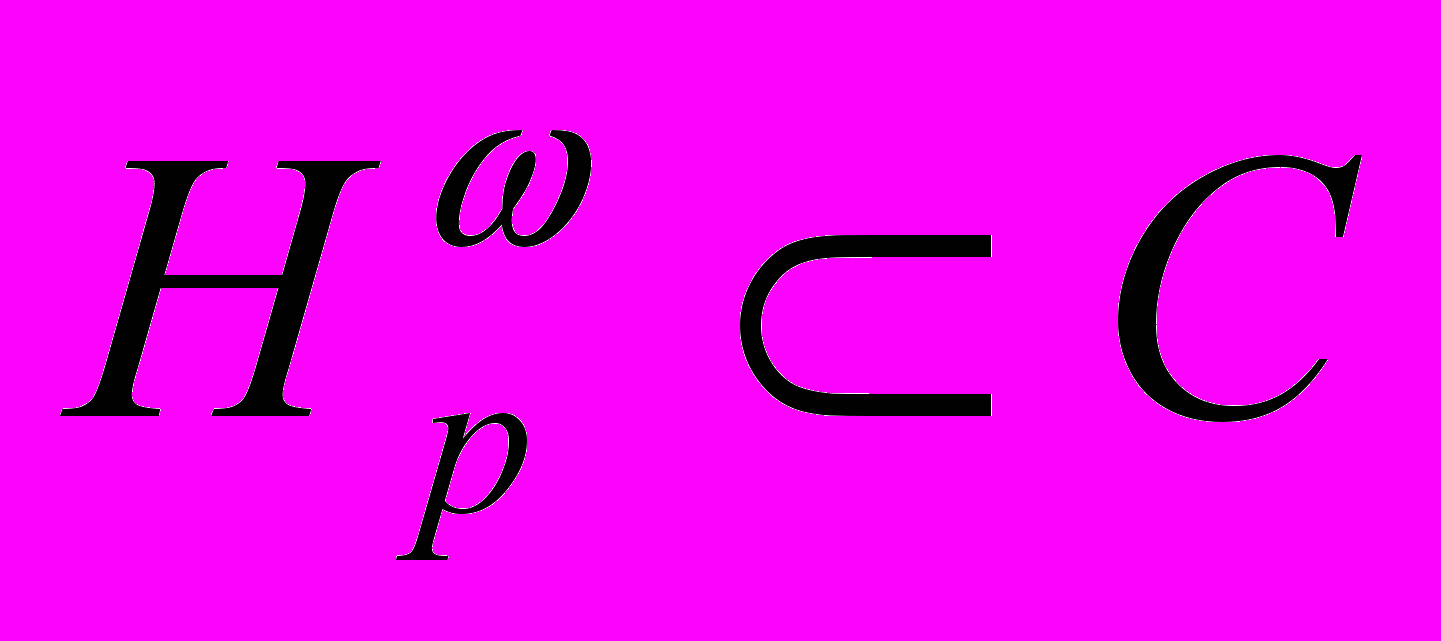имеет место тогда и только тогда, когда каждая функция из 
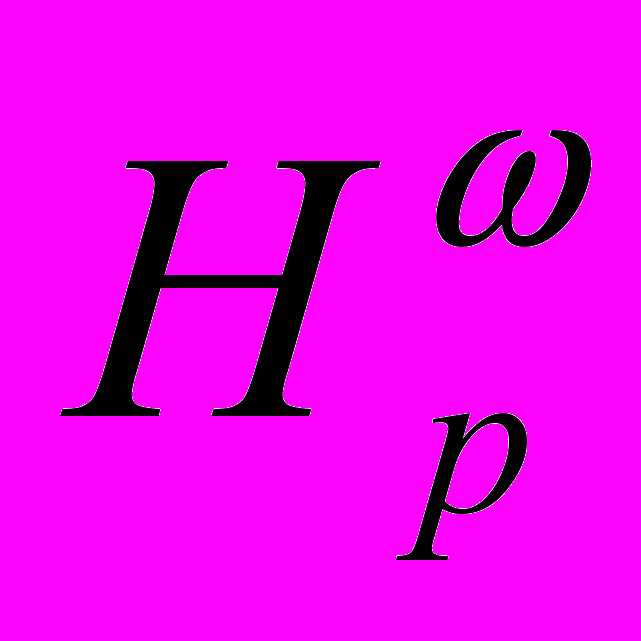раскладывается в равномерно сходящихся тригонометрический ряд Фурье и была высказано предположение, что существует аналогичная связь и в случае функций многих переменных.В статье устанавливается справедливость гипотезы Ульянова при суммировании тригонометрических рядов по Принсхейму, но не по сферам.
3. Об одной теореме вложения
(Изв. высш. учеб. завед. Математика, 1973, №7, стр. 103-111) ..…………………………………………….........23
Гипотеза Ульянова из предыдущей статьи была справедлива для классов
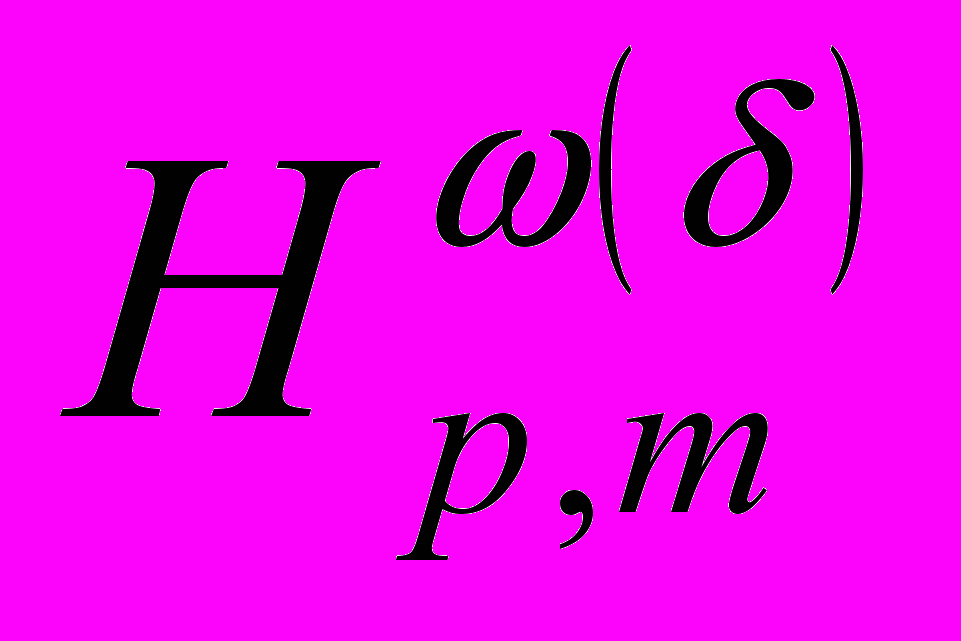в случае m переменных при 
, где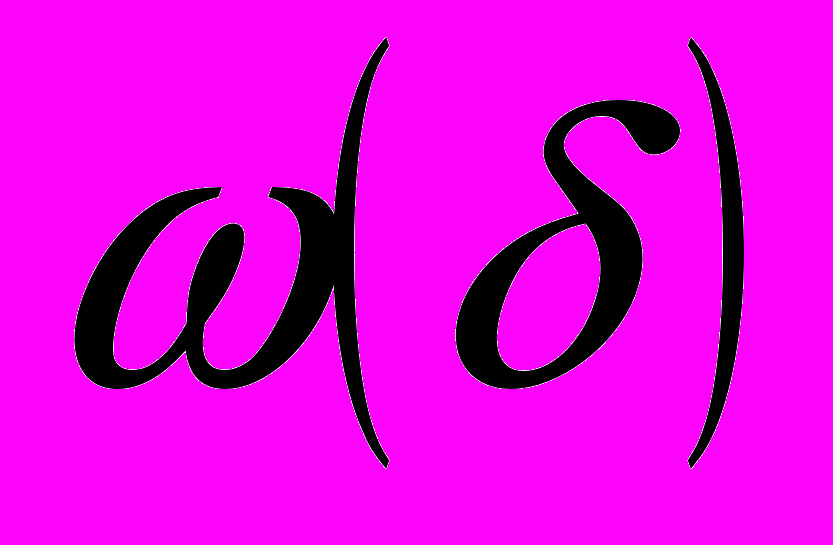 
- модуль непрерывности, но малосодержательна.Замена в определении класса модуля непрерывности на модуль гладкости порядка m+1 повлекла получение нетривиальной теоремы.
4. Об условиях принадлежности высших производных классам φ (L)
( Матем. заметки, 1973, т.14, №4, стр. 479-486) ……………………... …………………………………….…….31
Conditions under which hinder derivatives belong to the classes φ (L)
(Mat. zametki,1973, Vol. 14, No 4, pp.832-836)………………………………………………. ………………...…...39
Известный критерий Ф.Рисса 1910 года принадлежности производной абсолютно непрерывной функции пространству Lp, входящий во многие учебники, распространен на самый общий случай в шкале классов Орлича.
5. Об интегральном модуле непрерывности
(ACTA SCIENTIARUM MATHEMATICARUM, 1974, т. 36, №. 1-2, 173-180 (совм. с П. Л.Ульяновым))….........44
В доказательстве ранее известного обобщения теоремы Хилла-Клейна-Издзуми показана ошибка и дано верное доказательство.
6. О многомерном модуле непрерывности (2)
(Изв. АН КазССР, сер. физ.-матем. 1975, №5, стр. 89-90) .........................................................................................52
Получен многомерный аналог теоремы Хилла-Клейна-Издзуми -Ципсера.
7. О вложении некоторых классов функций
(Матем. заметки, 1976, т. 20, №6, стр. 835-841)……..................................................................................................54
The inclusion of certain classes of functions
(Mat. zametki, 1976, pp.1026-1030)…………………………………………………………………………………......61
По аналогии с критерием Ульянова
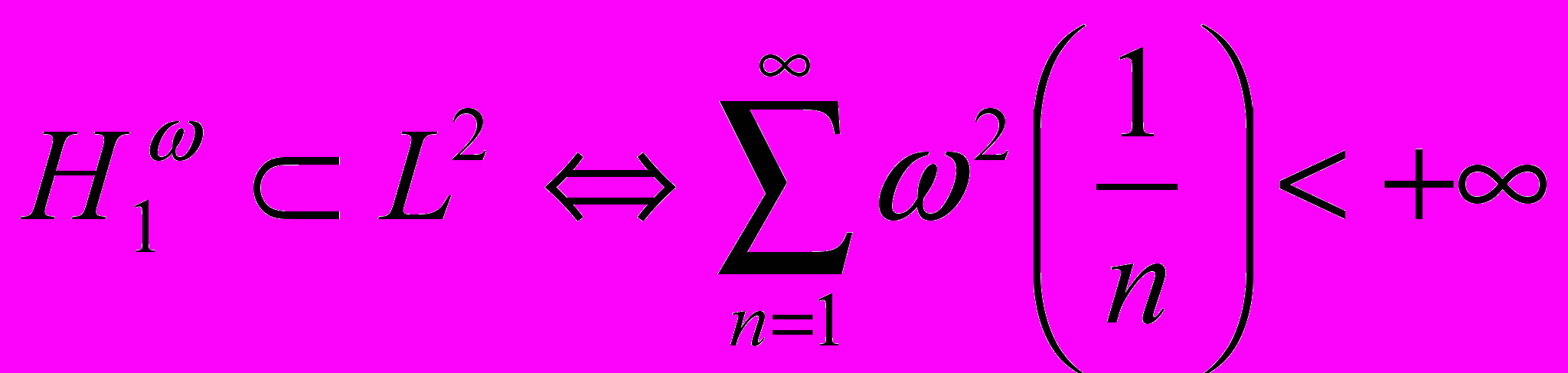для класса функций, определенного скоростью убывания наилучших приближений тригонометрическими многочленами установлен критерий
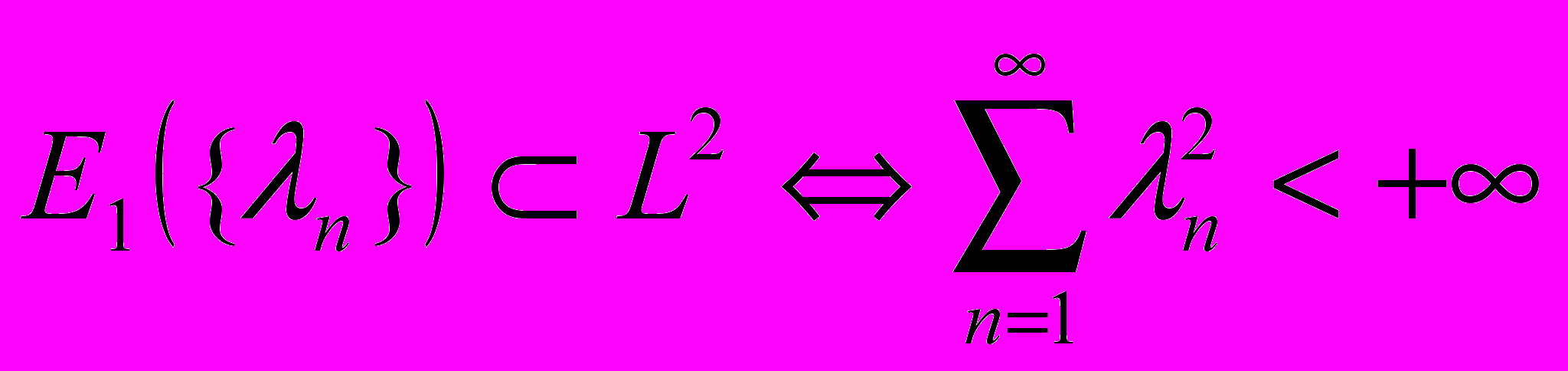.8. О вложении некоторых классов функций в С (
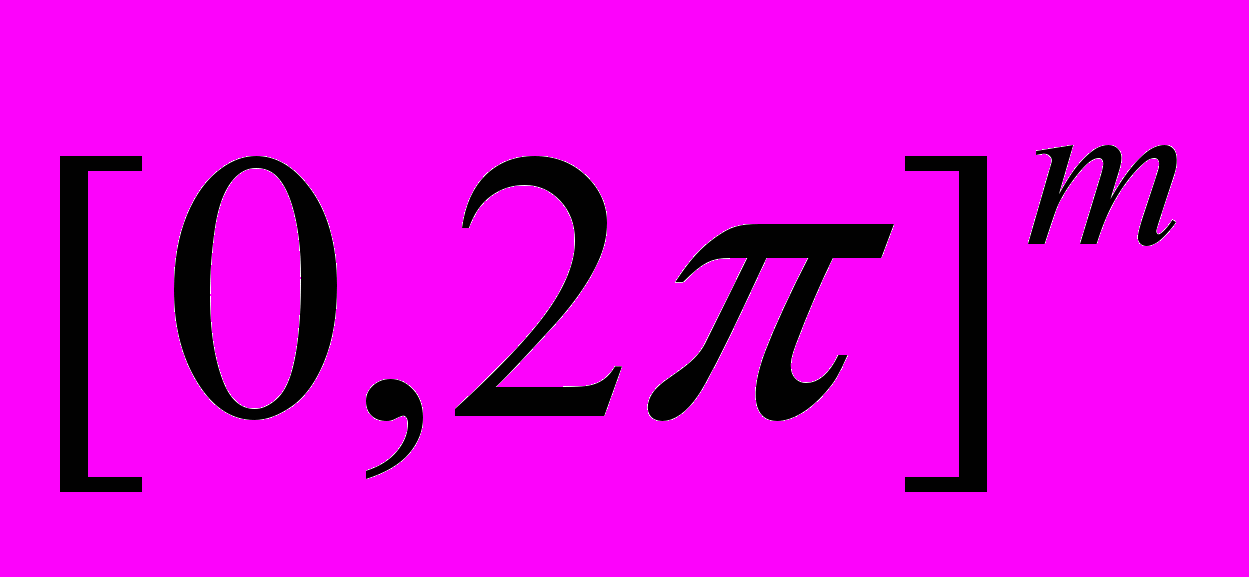)(Изв. высш. учеб. завед. Математика, 1978, т.20, № 8, стр. 88-90)….….. …………………………………...….....66
On imbedding classes of function into C([0, 1]m)
(Izvestiya Vuz. Matematika 1978, Vol.22, No.8, pp.69-71 ) ………………………………..……….…………….…....69
Показан, что многомерный аналог теоремы вложения Конюшкова – Стечкина классов функций, определяемых мажорантой на наилучшие приближения, для случая вложения в С неусиляем.
9. О вложении в некоторые пространства Лоренца
(Изв. высш. учеб. завед. Математика, 1980, №6, стр. 83-85)………………………………………………….……..72
On Embeddinic into some Lorentz spaces
(Izvestiya Vuz. Matematika 1980, Vol. 24, No.6, pp.101-103)…………………………………………………………69
10. О вложении классов
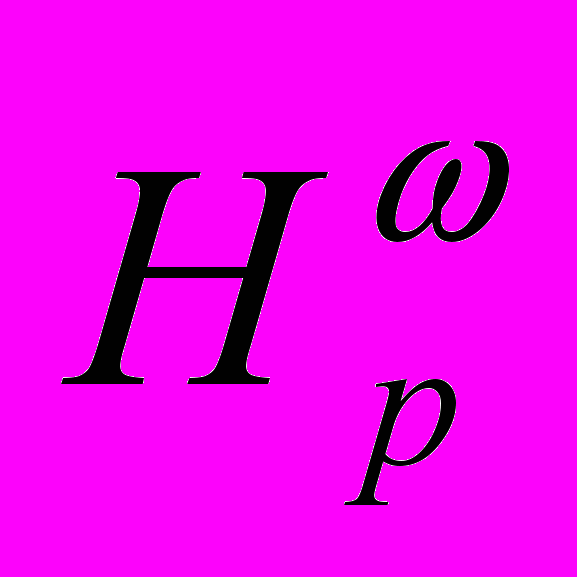в пространства Лоренца (Сиб. матем. журнал, 1983,т. XXIV, №2, стр. 160-172)…………………………………..……………...……….....78
Embeddings of the classes
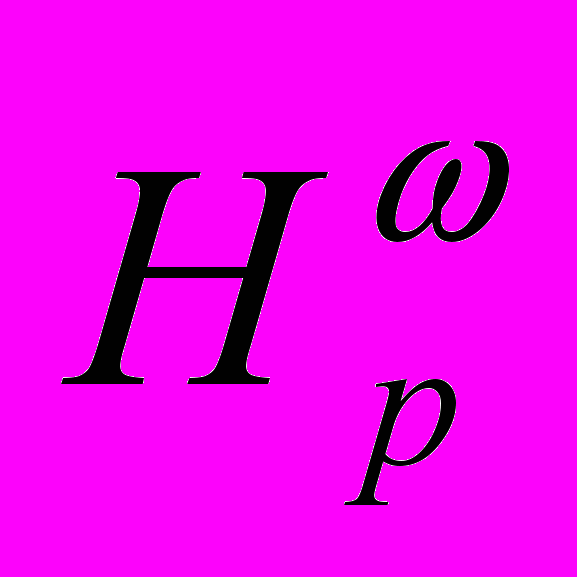in Lorentz spaces ( Sibirskii matematicheskii zhurnal, Vol.24, No.2, 1983, pp.287-298)……………………… …..……………………..91
В [9-10] обнаружен новый эффект в случае вложения классов
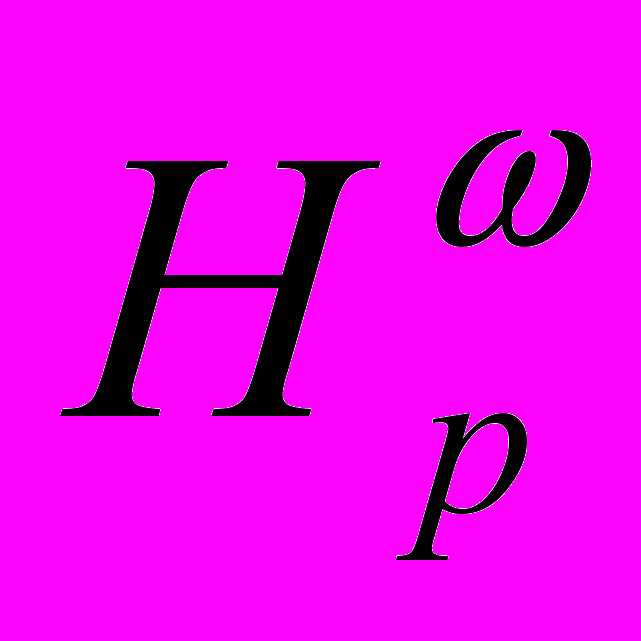в пространства Лоренца 
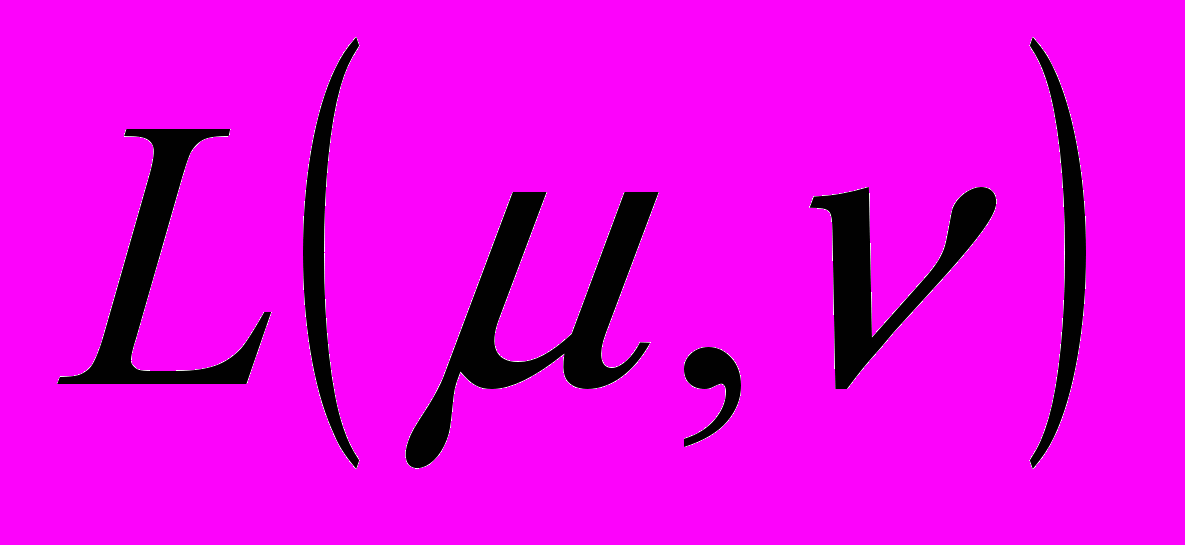, заключающейся в установлении различия случаев 
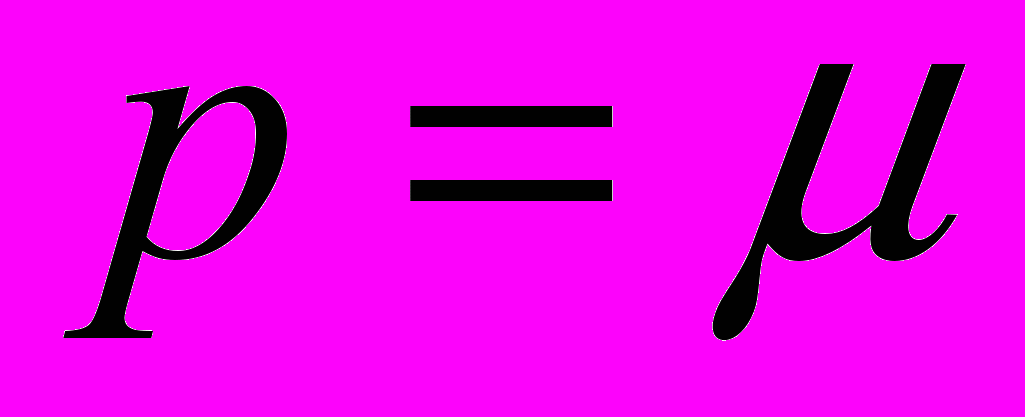и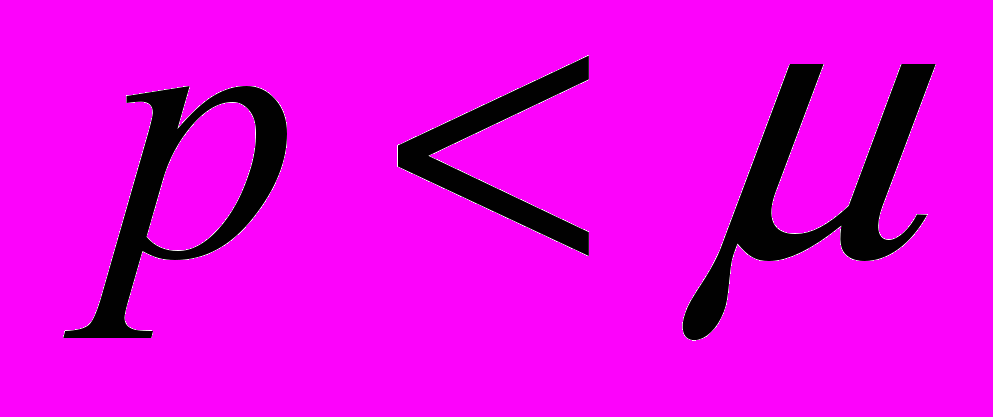 
.11. О некоторых задачах численного интегрирования
(Вестник АН КазССР, 1983, №12, стр. 15-18)…………..………………………………………...…..……….....102
А.В. Сульдин (1959 год) первый поставил и решил задачу оценки качества вычислительного агрегата «в среднем» относительно вероятностной меры (Винера).
Последующие работы (включая и работу С.М.Воронина и В.И. Скалыги) были выполнены относительно гауссовских мер.
Здесь, по видимому, впервые введена вероятностная мера на конкретном функциональном классе (Коробова
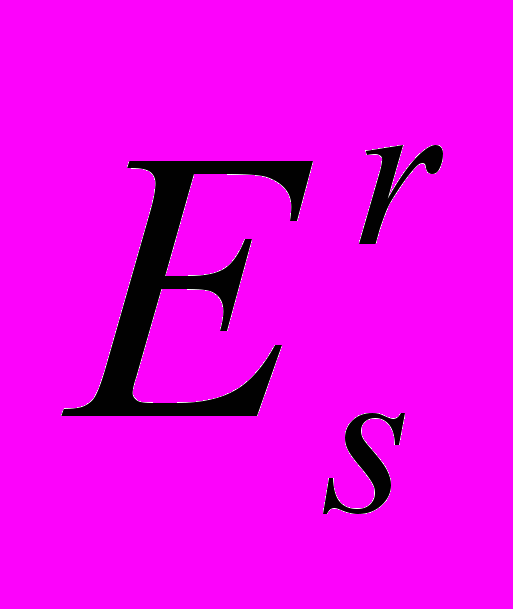), стало быть, негауссовская и относительно ее вычислены «средние квадратические погрешности» общих квадратурных формул и метода Монте-Карло.12. О некоторых приложениях меры Банаха
(Изв. АН КазССР, сер. физ.-матем., 1984, №5, стр. 8-11(совм. с С.М. Ворониным))………………...………..105
В силу равенства Парсеваля (теоремы Пифагора) меровведение на
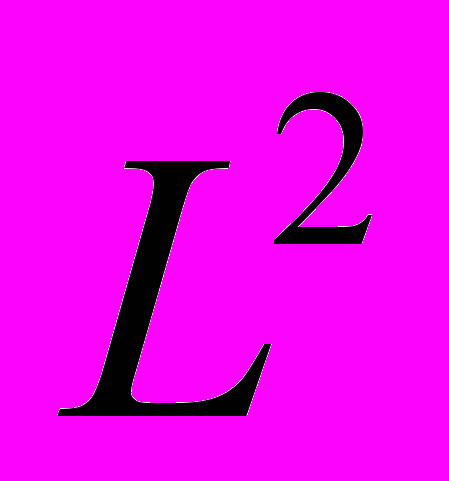- пространствах Соболева, Никольского-Бесова сводится к построению мер на весовых пространствах числовых последовательностей из коэффициентов Фурье. При этом, если на классах типа Коробова речь шла об условиях на индивидуальные коэффициенты Фурье, то здесь – на взвешенные ряды из коэффициентов Фурье.
Как оказалось, такого сорта меры ранее введены С.Банахом, техническую часть построения берет на себя теорема Колмогорова о меровведении на бесконечномерных пространствах.
В статье дана конкретизация построения мер на указанных выше
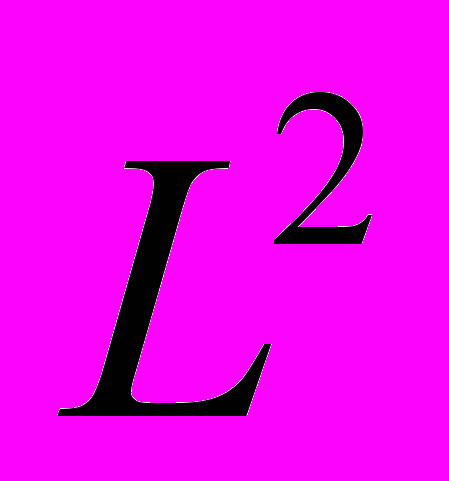-классах и их применения в вопросах квадратур. Другим, и, быть может, в смысле новизны более важным, является определение поперечника Колмогорова «в среднем»:
.Исследования этого поперечника впоследствии производились в ряде статей (см., напр, Creutzig J., Dereich S., Müller-Gronbach T., Ritter K. Infinite-Dimensional Quadrature and Approximation of Distributions // Found Comput Math (2009) 9: 391 - 429)
13. Об одном примере из теории меры
(Доклады расшир. засед. семинара Института прикл. математики им. И.Н. Векуа, 1985, т.1, №2, Тбилиси, стр. 140-143) ………………………………………………………………………………………….…….........................109
В 1985 году, в один из приездов в Алматы, В.М. Тихомиров поставил вопрос о «гибкости» погрешностей вычислительных агрегатов «в среднем», - каков диапозон их изменения при различном выборе вероятностей меры.
В статье на примере одномерного класса Коробова показана «абсолютная гибкость» относительно вероятностного меровведения: погрешности могут убывать с любой наперед заданной скоростью.
14. Об одном приложении меры Банаха к квадратурным формулам
(Матем. заметки, 1986, т. 39, №1, стр. 52-59 (совм. с С.М. Ворониным)) …………………………………...……112
Application of Banach measure to quadrature formulas
(Mat. zametki, 1986, Vol.39, No.1, pp.30-34)………………………………………………………………………....119
Найдены среднеквадратические погрешности детерминированных квадратурных формул и метода Монте-Карло относительно меры Банаха.
15. Об одном подходе к оценке качества интегрирования методом Монте-Карло
(Изв. АН КазССР, сер. физ.-матем.,1987, №1, стр. 16-20 (совм. с С.М. Ворониным)) …………………………..123
Для метода Монте-Карло определена вероятностная характеристика качества численного интегрирования, позволяющая в одних и тех же терминах сравнивать ее (метода Монте-Карло) эффективность с неслучайными алгоритмическими методами.
16. О вычислении экстремума функционала
(Изв. АН КазССР, сер.физ.-матем., 1987, №3, стр. 23-26 (совм. с С.М. Ворониным))…………….....……….....127
На основе введения борелевской меры на функциональном компакте предложен метод приближенного вычисления на том же компакте максимума модуля непрерывного функционала.
17. On an application of infinitely divisible distributions to qudrature problems
(Analysis Mathematica 14, 1988, №3, рр. 253-258)……………………………….………………………................130
Найдены среднеквадратические погрешности детерминированных квадратурных формул и метода Монте-Карло относительно мер, определенных безгранично делимыми распределениями.
18. О квадратурных формулах, связанных с дивизорами поля гауссовых чисел
(Матем. заметки, 1989, т. 46, №2, стр. 34-41 (совм. с С.М. Ворониным)) ……………………………..........….135
Quadrature formulas associated with divisors of the field of Gaussian numbers
(Mat. zametki, 1989, Vol.46, No2, pp.597-602)………….……………………...……………………….............…….143
Предложен способ построения квадратурных формул, основанный на теории дивизоров поля гауссовых чисел.
19. Применение теории дивизоров к приближенным восстановлению и интегрированию периодических функций многих переменных
(Докл. АН СССР, 1990, т. 310, №5, стр.1050-1054).………………………………………………………………..149
Соответственно анонсировано и даны доказательства применения теории дивизоров в задачах численного интегрирования и восстановления функции.
Дано в определенном смысле полное решение известной проблемы построения эффективных алгоритмов для нахождения сеток Коробова в квадратурных формулах с равными весами.
Сочетание теоретико-вероятностного подхода к задаче численного интегрирования с теоретико-числовым методом построения квадратурных формул.
20. Применение теории дивизоров к численному интегрированию периодических функций многих переменных
(Матем. сб., 1990, т. 281, №4, стр. 490-505)……………......................................................................................…..154
Application of divisor theory to the numerical integration of periodic functions of several variables (Matem. sbornik, 1990, pp. 527-542)…………..…………….… ………………….…............................170
Дано в определенном смысле полное решение известной проблемы построения эффективных алгоритмов для нахождения сеток Коробова в квадратурных формулах с равными весами.
Сочетание теоретико-вероятностного подхода к задаче численного интегрирования с теоретико-числовым методом построения квадратурных формул.
21. Средние квадратические погрешности алгоритмов численного интегрирования, связанных с теорией дивизоров в круговых полях
(Изв. высш. учеб. завед. Математика, 1990, №8, стр. 90-93)………………...………………………………….....186
Соответственно анонсировано и даны доказательства применения теории дивизоров в задачах численного интегрирования и восстановления функции.