Математика: наука
| Вид материала | Документы |
- Колмогоров Андрей Николаевич, 563.58kb.
- Задачи и упражнения по математическому анализу для втузов. Под ред. Б. П. Демидовича., 19.39kb.
- Византийская математика, 186.7kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Расшифровка : Математика, 146.94kb.
- Что такое прикладная математика?, 81.59kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
- Программа Фестиваля Мероприятия мгу им. М. В. Ломоносова, 971.43kb.
§5. Алгебраическая теория чисел и гармонический анализ в задачах численного интегрирования…………………..………………….……………………………………………..86
А. Квадратурные формулы
1. Постановка задачи численного интегрирования……...………..………………………………86
- Уточнение постановок задачи (1-2)………………….…………………………..…………….88
В. Теоретико-числовые методы в задачах численного интегрирования. Введение.……………………………………..……………………………..………………………..89
- Краткий обзор теоретико-числовых методов в численном интегрировании………………..90
- Теоретико - числовые алгоритмы приближенного интегрирования (случай
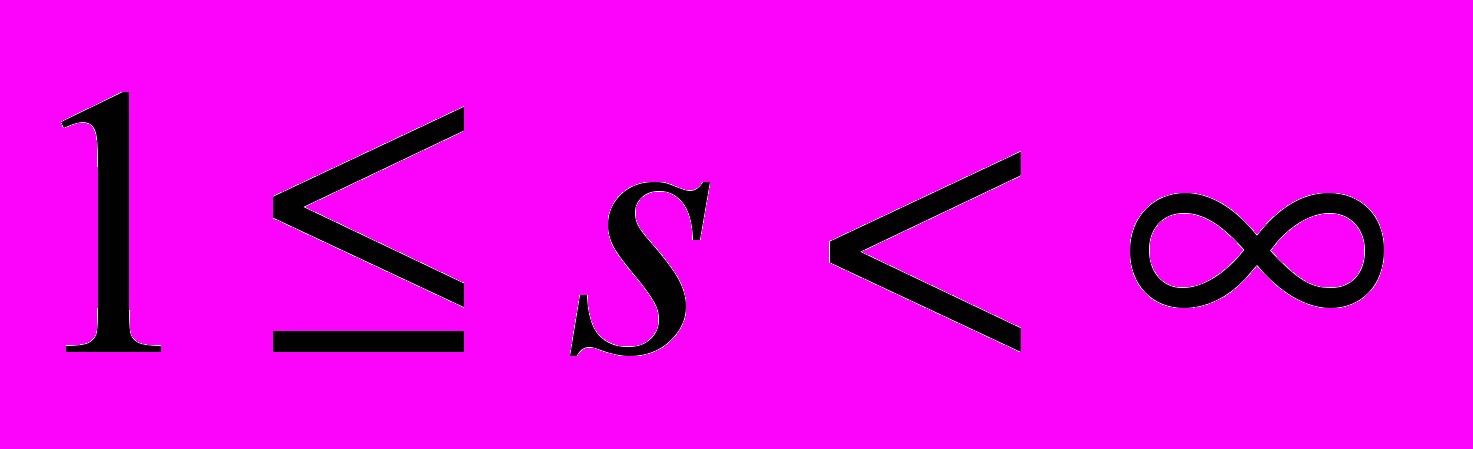 )……………………………………………………………………………...…………..92
)……………………………………………………………………………...…………..92- Теоретико - числовые алгоритмы приближенного интегрирования (случай
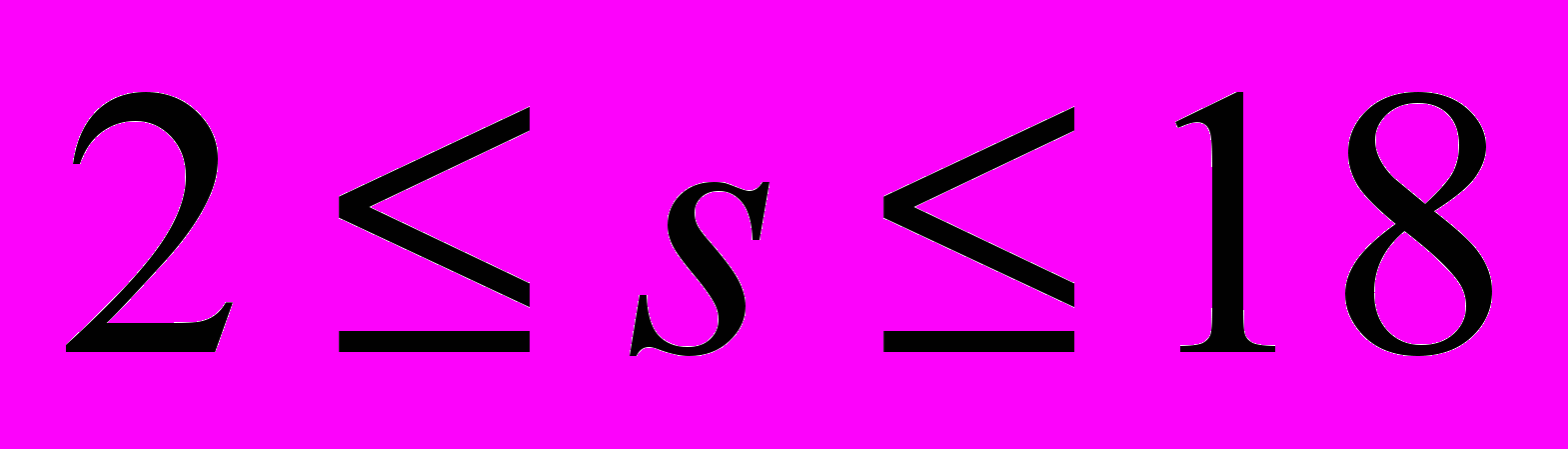 )………………………………………………………………………………..………94
)………………………………………………………………………………..………94- Об эквивалентных условиях равномерной распределенности сеток Коробова……………..95
- Комментарии и замечания………………………………………………………………………..96
- Построение равномерно распределенных сеток Коробова методом вычислительных экспериментов……………………………………………………………………...………………..97
С. Построение равномерно распределенных сеток Коробова методом вычислительных экспериментов…………………………………………………………………………..…………...98
D. Еще о теоретико-числовых методах
1. Комбинированные теоретико-числовые сетки…………………………….……………..……106
- Метод квази-Монте Карло (КМК)……………………….….………...………………………107
Е. Численное интегрирование бесконечно дифференцируемых функций (теорема Е. Нурмолдина)…………………………………………………….………………………………….107
Перспективы......................................................................................................................................109
§6. Применение тензорных произведений функционалов в задачах численного интегрирования……..………………………………………………………….…………………113
Введение………………………………………………………………………………..…………...113
- Конкретизация общего метода тензорного произведения функционалов для случая квадратурных формул Смоляка………………………………...…………………………………116
- Квадратурные формулы
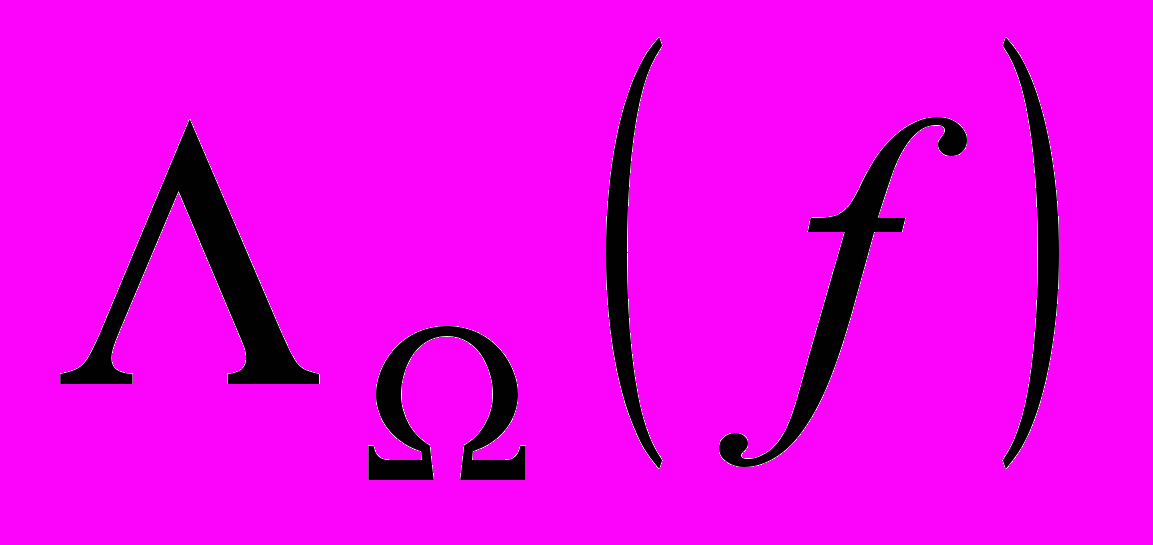 для классов
для классов 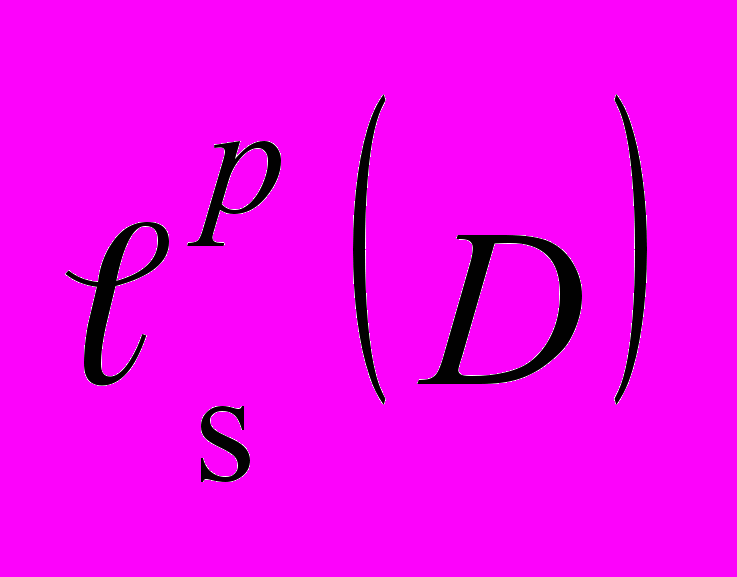 …………………...…………………..…117
…………………...…………………..…117
- Квадратурные формулы
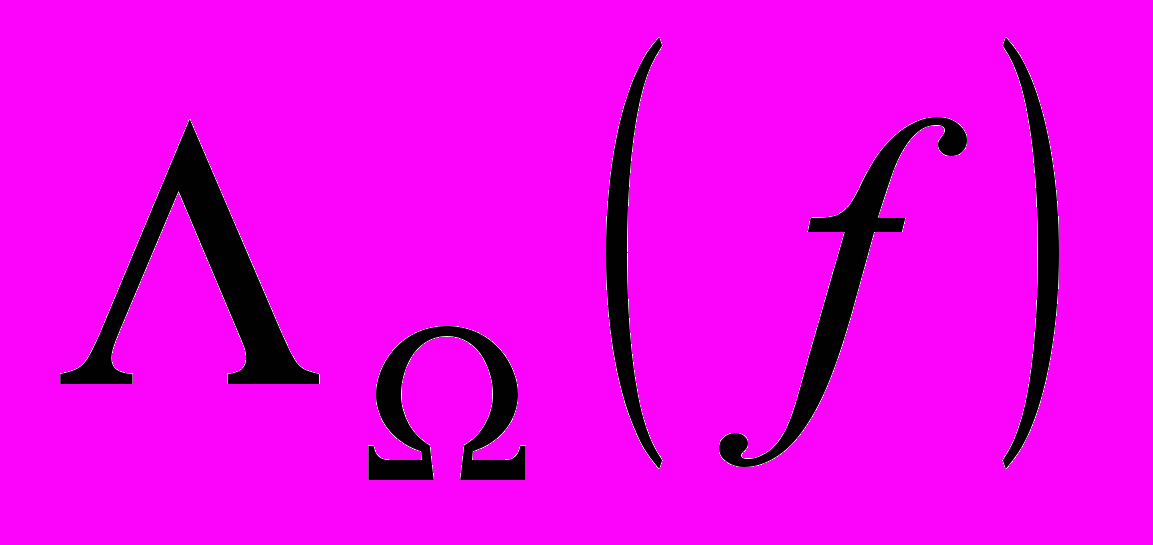 для классов
для классов 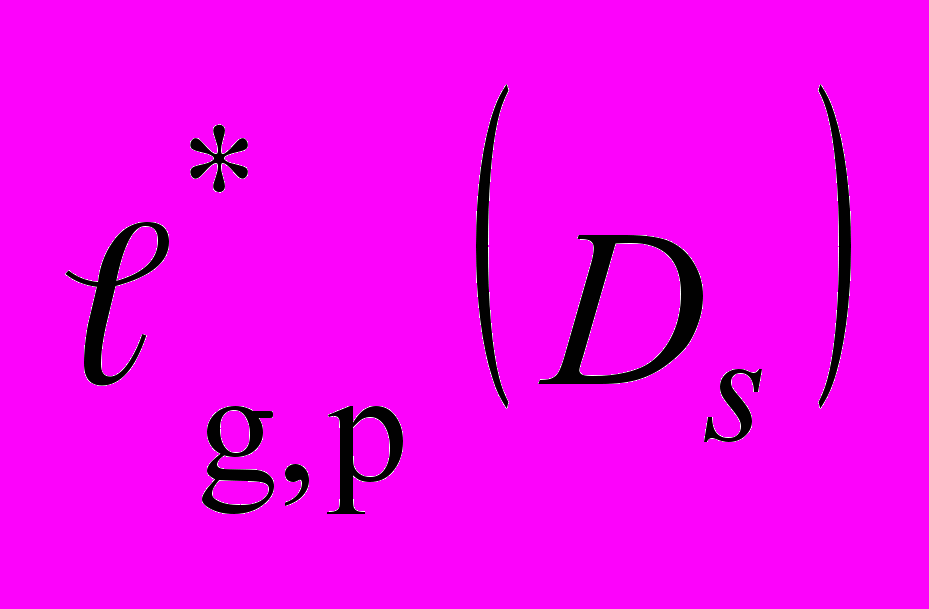 …………………...…………….………121
…………………...…………….………121
- Неэффективность квадратурных формул Смоляка при повышении гладкости до
бесконечной………………………………………………………...…………………..………122
- К вопросу о влиянии начального параметра в квадратурной формуле Смоляка……….....123
- О порядке дискрепанса сетки Смоляка…………………………………………………..….123
- О качестве сеток в квадратурных формулах (задача Сарда)………………………...……...124
- Численное интегрирование тригонометрических коэффициентов Фурье……….……….127
- Применение тензорных произведений функционалов к квадратурным формулам
Коробова (Н.Темиргалиев, Д.Кулбаева)…………………………………………..………....131
- Оценки погрешностей квадратурных формул по неточной информации для
классов
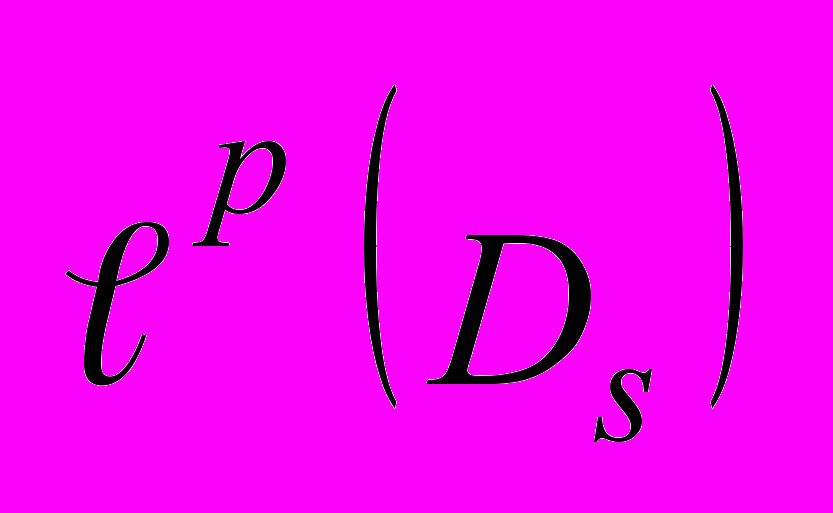 и
и 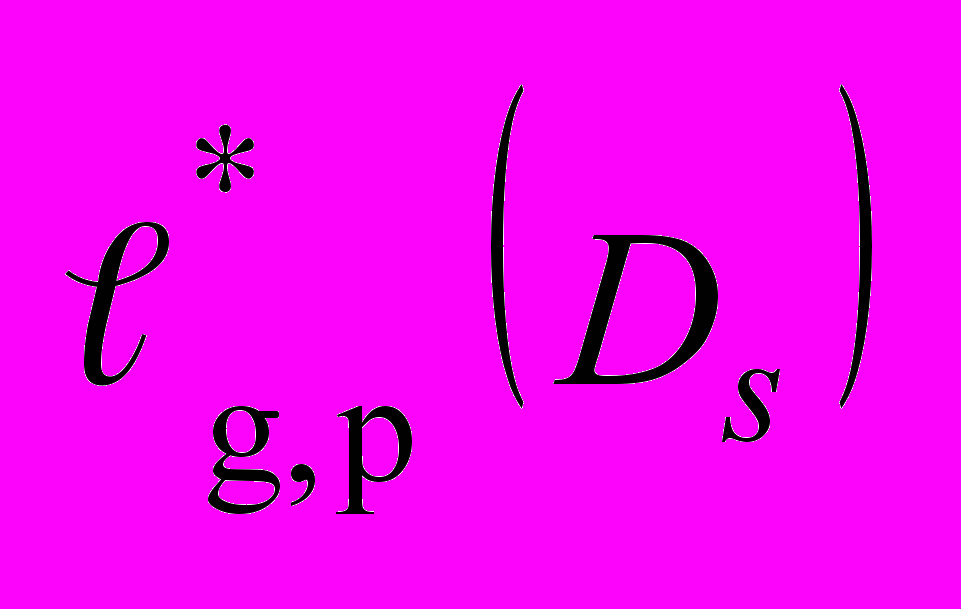 ……………………………………..……………..……………………..134
……………………………………..……………..……………………..134- Тензорные произведения функционалов относительно систем Чебышева……...………...135
- Дальнейшее развитие темы……………………………………………………..…………….135
§7. Восстановление функций………………..…………………………………….………….…138
- Задача восстановления функций из классов……………………………………………….…138
- Эффективизация ранее известных теорем существования операторов восстановления функций……………………………………………………………………………………………..141
- Информативная мощность всех возможных линейных функционалов при восстановлении функций из классов……………………………………………………………………………...…142
- Метод К.Шерниязова (Применение квадратурных формул к восстановлению функций и преобразованных рядов Фурье)……………………………………...……………………………145
- Формула К.Шерниязова о восстановлении преобразованных рядов Фурье по значениям в точках суммы исходного ряда………………………………………..…………………………145
- Восстановление функций и преобразованных рядов Фурье по значениям суммы исходного ряда……………………………………………………………………….……………………...…147
- Восстановление функций из классов методом тензорных произведений функционалов……………………………………………………………...……………………….149
- Операторы восстановления функций – перспективы дальнейших исследований……...…154
- Восстановление преобразованных рядов Фурье по значениям суммы исходного ряда…………………………………………………………………………………...……………..154
- Восстановление бесконечно дифференцируемых функций……………..…………………155
