Что такое прикладная математика?

Вид материала

Содержание

Различия между «чистой» и «прикладной» математикой

Подобный материал:

Что такое прикладная математика?

Наука лишь тогда достигает совершенства, когда ей удается пользоваться математикой (К. Маркс)

Под прикладной математикой понимают ту часть математики, которая находит приложение в других сферах научной и практической деятельности человека. И. И. Блехман, А. Д. Мышкис и Я. Г. Пановко определяют прикладную математику как науку об оптимальных, практически приемлемых методах решения математических задач, возникающих вне математики. В этом определении обращается внимание на то, что задачи, которые решает прикладная математика, возникают в других науках под воздействием практических потребностей, поэтому и решения таких задач должны быть в определенном смысле оптимальными и практически приемлемыми.

Различия между «чистой» и «прикладной» математикой

	«Чистая» математика	«Прикладная» математика
Направление движения в познании	от конкретного к абстрактному При образовании понятий отвлекаются от конкретного, специфического содержания объектов и отношений. Получаются абстрактные объекты (числа, геометрические фигуры, функционалы, пространства, алгебраические структуры).	от абстрактного к конкретному Абстрактным структурам чистой математики придается определенный смысл и значение, и они применяются для изучения предметов и процессов реального мира. (См. пример после таблицы).
Способы рассуждений	Дедуктивный (логический) способ вывода утверждений из небольшого числа исходных посылок, точные определения понятий	Нестрогие рассуждения и способы образования понятий, эмпирические методы исследований
Проблема существования	Существование объекта устанавливается с помощью логических рассуждений, часто проводится неконструктивное доказательство от противного	Указание способа построения объекта и методов, с помощью которых результат может быть найден с необходимой точностью за допустимый промежуток времени
Бесконечность	Бесконечность – одно из важнейших понятий, лежащих в основе понятий предела, интеграла, бесконечно малых и бесконечно больших функций	На практике люди имеют дело только с конечными вещами и процессами, но есть достаточно большие и малые величины

Пример.

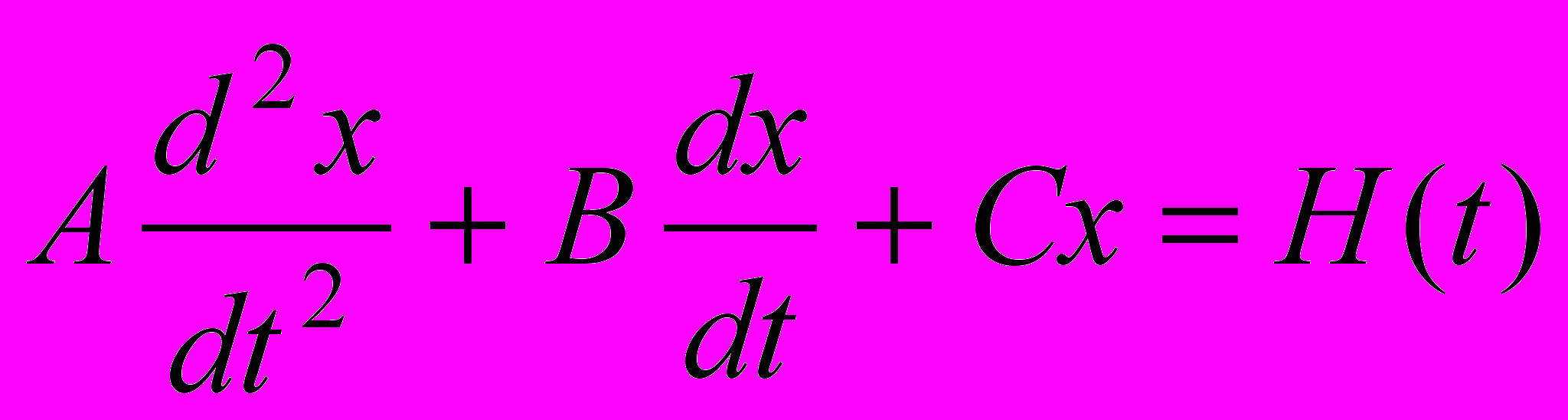
Это уравнение является моделью чистой математики. Моделью прикладной математики оно станет лишь тогда, когда его коэффициенты и отдельные члены получат соответствующую интерпретацию. Если толковать A как массу, а

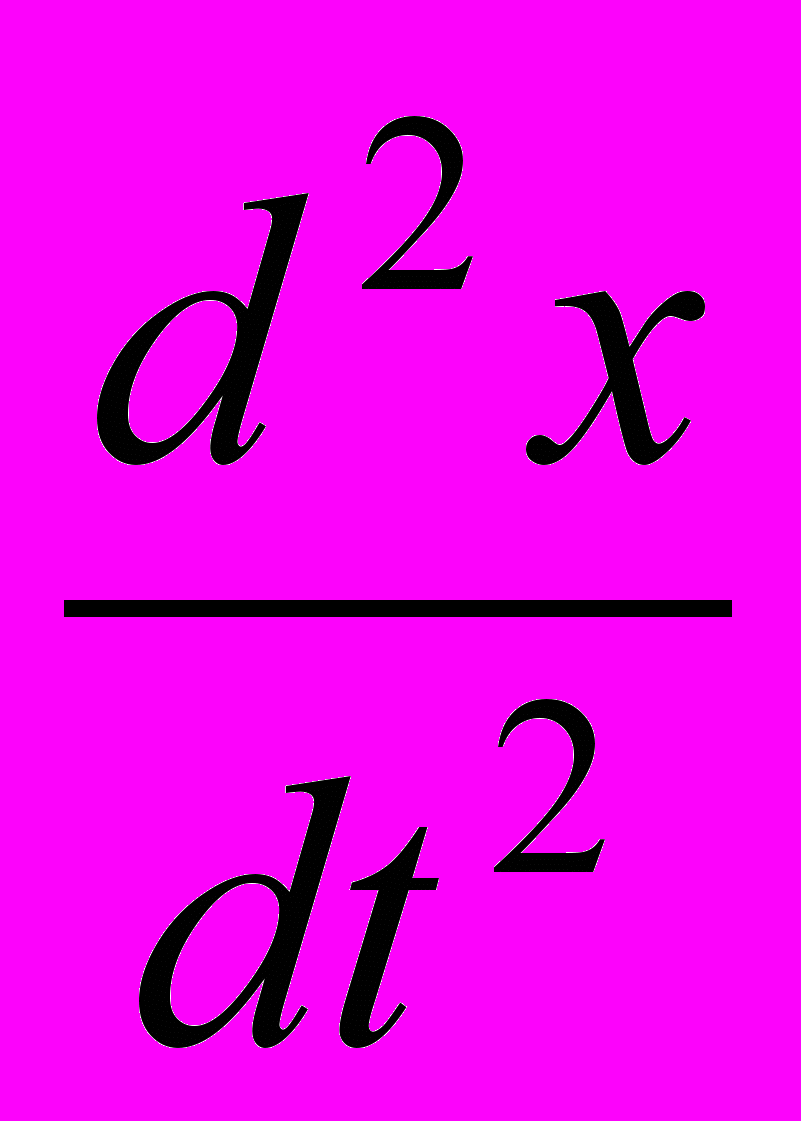как ускорение, то вышеприведенное уравнение будет служить моделью механических колебаний. Если же интерпретировать A как индуктивность, а

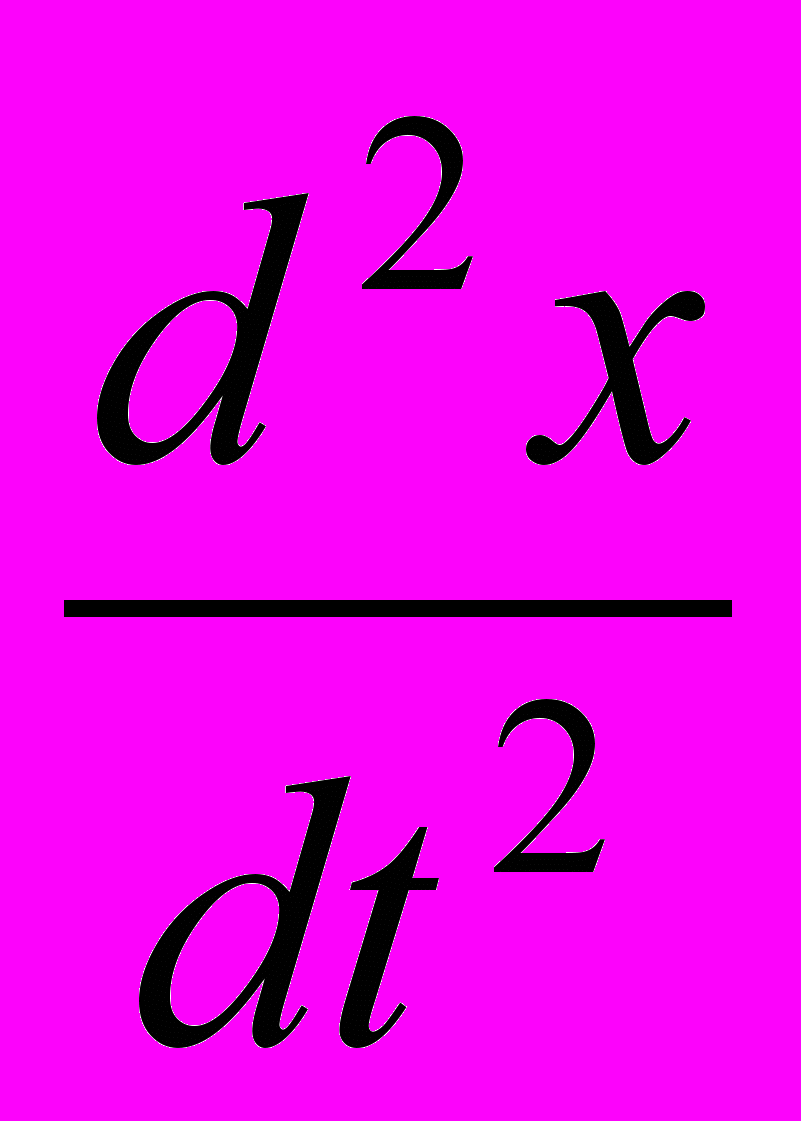как скорость изменения силы тока, то уравнение будет представлять модель электромагнитных колебаний. Данный пример показывает не только отличие моделей чистой и прикладной математики, но и демонстрирует тот факт, что различным по своей природе явлениям и процессам может соответствовать одна и та же математическая модель.

Разумеется, границы между чистой и прикладной математикой размыты и подвижны. Те результаты, которые считались чисто теоретическими, нередко находят практическое применение, хотя период времени между получением математических результатов и их применением может быть очень большим. Когда Аполлоний (Греция, II век до н. э.) изучал конические сечения, эта проблема была, очевидно, чисто теоретической. Однако, если бы свойства эллипса не были изучены Аполлонием, то Кеплер (начало XVII века), возможно, не смог бы установить, что планеты движутся по орбитам, имеющим форму эллипса. Но часто бывает и наоборот, – потребности решения тех или иных практических задач приводят к необходимости получения новых математических результатов и даже появлению новых математических дисциплин. Так, например, Ньютон, создавая основы математического анализа, исходил из необходимости решения практических задач. Решению практических задач обязана своим появлением теория вероятностей, линейное программирование, оптимальное управление и другие математические дисциплины.

Теоретическая (чистая) и прикладная математика развиваются в тесной взаимосвязи, обогащая друг друга. После того, как новое направление в математике возникает из-за необходимости решения практических задач, оно начинает далее развиваться по своим внутренним законам, часто уходя далеко от потребностей практики. Для людей, которые пользуются готовыми выводами, формулами и уравнениями математики, наиболее ценными являются именно конечные продукты математического исследования, но они были бы невозможны без предварительной теоретической работы в области чистой математики.

Нередко прикладную математику понимают слишком узко, отождествляя ее с вычислительной математикой. Выражение результатов исследований в числах, использование различных вычислительных методов и техники, несомненно, имеют большое значение, но прикладная математика не сводится к вычислительной математике, так как для решения задач прикладной математики необходимы, кроме вычислительных, многие другие методы.

Типы моделей

Физические модели

Увеличенное ли уменьшенное описание объекта (системы). В некотором смысле такая модель выглядит как моделируемая целостность. Примерами таких моделей является копия конструируемого самолета (корабля, здания), выполненная с соблюдением пропорций в некотором масштабе. Свойства реального объекта исследуются на примере этой модели. Например, модель самолета продувают в аэродинамической трубе, а полученные показания тщательно исследуют. Модель здания помещают в аэродинамическую трубу, в которой моделируется роза ветров той местности, в которой предполагается строительство здания.

Аналоговые модели

Так называют модели, представляющие исследуемый объект аналогом, который ведет себя как исследуемый объект, но не выглядит как таковой.

Пример.

Пусть требуется найти наиболее экономичный способ регулярных известных поставок товаров в три города, построив для этого только один склад. Основное требование – место для склада должно быть таким, чтобы полные транспортные расходы были наименьшими (считаем стоимость перевозки равна произведению расстояния от склада до пункта назначения на общий вес товаров и измеряется в тонна-километрах).

Наклеим карту местности на лист фанеры. В месте нахождения городов проделаем отверстия, пропустим через них нити и привяжем грузики, вес которых пропорционален запросам товаров в города. Свяжем свободные концы нитей в один узел и отпустим. Под действием силы тяжести система придет в состояние равновесия. То место на листе фанеры, которое займет узел, будет соответствовать оптимальному расположению склада.

Математические модели

Так называют модели, использующие для описания свойств и характеристик объекта или события математические символы и методы. Математический подход прост потому, что подчиняется вполне определенным жестким правилам.

Если мы хотим использовать математические методы при решении задач, относящихся к какой-либо технической, экономической, биологической или любой другой системе, нам необходимо прежде всего построить математическую модель этой системы. Построить модель – это значит указать, какими математическими объектами характеризуется изучаемая система и как в этих математических понятиях отражаются те законы, которые описывают функционирование этой системы. Поскольку математическая модель не может отобразить изучаемую действительность во всей ее конкретности и полноте, то при ее построении выбирают такие факторы и взаимосвязи, которые являются наиболее существенными. Во многих случаях правильно выбрать модель – значит решить задачу более чем наполовину. Основная трудность при этом заключается в том, что при построении модели требуется соединение специальных (для изучения качественных особенностей моделируемого процесса) и математических знаний. В прошлом математик сам мог выступать специалистом в конкретной области научного знания (Ньютон, Лагранж, Лаплас, Гаусс и др.). В силу возрастающего количества научной информации и углубляющегося процесса дифференциации наук одному ученому стало невозможно работать в нескольких отраслях знания. Поэтому для построения модели и эффективного решения поставленной математической задачи (особенно когда речь идет о крупных научных проблемах) необходимо сотрудничество ученых различных специальностей и, конечно, привлечение современной вычислительной техники.

При построении математической модели могут встретиться и непреодолимые трудности:

неизученность законов, описывающих систему (в биологии, экономике);
неизвестность характеристик системы (плотность распределения вещества в толще Земли; давление в сосудах живого организма).

В этом случае при построении модели приходится делать дополнительные предположения, которые носят характер гипотез. Следовательно, выводы, полученные в результате исследования такой модели, носят условный характер. Но даже если законы известны и характеристики системы измерены, модель может получиться столь сложной, что будет недоступна для изучения известными математическими методами. Поэтому часто при моделировании реального процесса приходится принимать некоторые упрощения, идеализировать модель.

Таким образом, построение математической модели должно удовлетворять двум важнейшим критериям:

модель должна быть адекватной, т. е. соответствовать действительности;
модель должна быть простой и позволять находить эффективное решение за приемлемое и с достаточной точностью.

Нетрудно заметить, что эти критерии противоречат друг другу. С одной стороны, построение адекватной модели требует учета все более полного и разнообразного количества факторов, что неизбежно усложняет модель. Такое усложнение приводит к тому, что поставленную проблему не удается решить вообще или за практически приемлемое время. С другой стороны, чрезмерно простая модель, в которой не принимается во внимание ряд существенных факторов, оказывается заведомо неадекватной и потому не отвечающей своему назначению. Искусство исследователя состоит в том, чтобы найти гармоничное соответствие этих двух взаимно несовместимых требований. При прочих равных условиях необходимо стремиться к тому, чтобы модель соответствовала действительности. Но степень этого соответствия должна определяться условиями поставленной задачи, т. е. модель должна давать приблизительно верное отражение реальности.

Этапы решения прикладной задачи с помощью математических методов:

Корректная формулировка прикладной задачи, заключающаяся в выделении существенных свойств и взаимосвязей изучаемого объекта или процесса.
Построение математической модели, – отображение количественных отношений выделенных на первом этапе свойств с помощью математических понятий и соотношений. Как отмечалось выше, это самая трудная часть исследования. Во-первых, для одних и тех же явлений могут быть построены самые разнообразные математические модели. Во-вторых, необходимо, чтобы построенная модель удовлетворяла требованиям адекватности и простоты.
Логико-математический анализ модели: проверка модели на непротиворечивость и решение поставленной математической задачи. Иногда реализация этого этапа требует развития новых методов или даже создания новой математической дисциплины. Решение поставленной математической проблемы не всегда может быть найдено по какой-либо конкретной формуле, даже если оно существует. Поэтому могут потребоваться численные методы решения, – т. е. методы, дающие не точный, а приближенный (с достаточной степенью точности) ответ. Данный этап включает в себя теоретическое исследование математической проблемы и ее практическое решение (в том числе сбор исходных данных, программирование).
Интерпретация результата с помощью известного эмпирического материала (результатов наблюдений или специально поставленных экспериментов), т. е. перевод математического ответа на язык конкретной науки.
Проверка полученных результатов на практике. Возможно, этот этап (впрочем, как и предыдущие) потребует уточнения и модификации модели, т. е. возвращения к предыдущим этапам (даже к первому).

Blog

Что такое прикладная математика?

Содержание

Различия между «чистой» и «прикладной» математикой