40. Динамические экспертные системы
| Вид материала | Документы |
СодержаниеДостоверность работы цифровых устройств |
- Курс лекций "Экспертные системы" (Для студентов заочного обучения юридического факультета, 84.44kb.
- 4 Экспертные системы, 51.16kb.
- 14. Лекция: Позиционно-силовое управление в системе робота-станка, 113.23kb.
- Алгоритмы обучения и архитектура нейронных сетей. Нейросетевые системы обработки информации, 21.42kb.
- Программа дисциплины «Динамические системы» Направление, 73.11kb.
- Рабочая программа дисциплины «Дискретные динамические системы», 110.59kb.
- Говоря простым языком, системы баз знаний это искусство, которое использует достижения, 267.75kb.
- Лекция №15. Экспертные системы Экспертные системы зародились в ходе развития методов, 188.15kb.
- Динамика системы управления гидротурбиной с пидрегулятором, 80.14kb.
- О некоторых особенностях интегрирования обыкновенных дифференциальных уравнений, описывающих, 18.79kb.
56. Методы точной оценки надежности цифровых устройств
^ Достоверность работы цифровых устройств
с функциональным диагностированием встроенными
средствами контроля
Оценим достоверность работы цифрового устройства с аппаратным контролем в соответствии с общей структурной схемой аппаратного контроля (см. рис. 2 а).
Обозначим через kn коэффициент избыточного оборудования
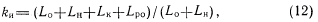
где Lo, LH — объем оборудования исходной контролируемой схемы соответственно охваченной и неохваченной аппаратным контролем (неконтролируемая часть схемы); (L0+LH),
, 
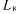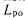— объем оборудования соответственно схем исходной, контроля, решающего органа.Принимая во внимание, что обычно
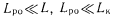формулу (12) перепишем в виде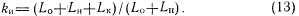
Будем также предполагать, что исходная схема и схема контроля выполнены на однотипных логических элементах, тогда (13) можно записать как
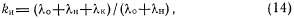
где
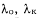— интенсивности отказов части исходной контролируемой схемы соответственно охваченной и неохваченной аппаратным контролем; кк — интенсивность отказов схемы контроля.Полноту контроля определим через коэффициент полноты контроля
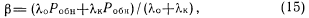
где
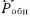— вероятность обнаружения ошибок выбранным методом контроля. Величина 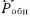в общем случае зависит от числа контролируемых разрядов, вероятности появления ошибок кратности if и т. п.Для инженерных расчетов можно пользоваться значениями величины
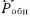, полученными по следующим формулам:контроль на четность
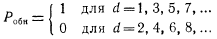
контроль по модулю вида
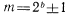
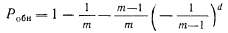
при условии, что надежность схемы контроля намного превышает надежность исходной схемы и n>d, где п — число разрядов исходной схемы или число разрядов в векторе выхода.
Числовые значения вероятности обнаружения ошибок для различных значений т и d приведены в табл. 4.
Таблица 4
| d | | | Робн | | | |
| т = 3 | m = 5 | | | т = 7 | т = 11 | |
| 1 2 3 | 1 0,5 0,75 | 1 0,75 0,812 | | | 1 0,833 0,861 | 1 0,9 091 |
Контроль с использованием корректирующих кодов
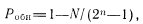
где N=2h — мощность множества разрешенных кодовых слов; (2n—1) —общее число возможных ошибок; к — число информационных символов (п, k) кода.
Рассмотрим два случая:
схема контроля контролируется полностью;
схема контроля не контролируется.
Для первого случая составим таблицу истинности булевых функций (табл. 5), соответствующих событиям
,
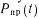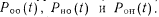Булевы функции определим следующим образом.Если схема работает правильно, припишем этому событию значение булевой единицы, в противном случае — значение булевого нуля. Событию, когда выбранный метод контроля позволяет обнаруживать ошибки, припишем значение булевой единицы, событию, когда выбранным методом контроля ошибки не обнаруживаются, припишем значение булевого нуля. Обозначим безотказность оборудования в исходной схеме охваченной аппаратным контролем р„, безотказность оборудования неохваченного аппаратным контролем р1и безотказность схемы контроля рк.
| Po | Рн | Рк | Робн | Рир | Роо | Рно | Ро | Рн | Рк | Робн | Рир | Роо | Рно | Рон |
| 0 | 0 | 0 | 0 | | | 1 | 0 | 0 | 0 | 0 | | | 1 | |
| 0 | 0 | 0 | 1 | | 1 | | 0 | 0 | 0 | 1 | | | 1 | |
| 0 | 0 | 1 | 0 | | | 1 | 0 | 0 | 1 | 0 | | | 1 | |
| 0 | 0 | 1 | 1 | | 1 | | 0 | 0 | 1 | 1 | | 1 | | |
| 0 | 1 | 0 | 0 | | | 1 | 0 | 1 | 0 | 0 | | | 1 | |
| 0 | 1 | 0 | 1 | | 1 | | 0 | 1 | 0 | 1 | | | 1 | |
| 0 | 1 | 1 | 0 | | | 1 | 0 | 1 | 1 | 0 | | | 1 | |
| 0 | 1 | 1 | 1 | | 1 | | 0 | 1 | 1 | 1 | | 1 | | |
| 1 | 0 | 0 | 0 | | | 1 | 1 | 0 | 0 | 0 | | | 1 | |
| 1 | 0 | 0 | 1 | | 1 | | 1 | 0 | 0 | 1 | | | 1 | |
| 1 | 0 | 1 | 0 | | | 1 | 1 | 0 | 1 | 0 | | | 1 | |
| 1 | 0 | 1 | 1 | | | 1 | 1 | 0 | 1 | 1 | | | 1 | |
| 1 | 1 | 0 | 0 | | | 1 | 1 | 1 | 0 | 0 | | | | 1 |
| 1 | 1 | 0 | 1 | | | | 1 | 1 | 0 | 1 | | | | 1 |
| 1 | 1 | 1 | 0 | 1 | | | 1 | 1 | 1 | 0 | 1 | | | |
| 1 | 1 | 1 | 1 | 1 | | | 1 | 1 | 1 | 1 | 1 | | | |