40. Динамические экспертные системы

Вид материала

Документы

Содержание 49. Цифровая подпись. Системы цифровой подписи на основе криптосистем с открытым ключом. 50. Хэш-функции. Использование хэш-функций в системах цифровой подписи. 51. Показатели надежности систем без восстановления и с восстановлением. Q(t) —вероятность появле­ния отказа щ течение времени i. P(t) монотонно убывающая (в процессе эксплуатации или хранения надежность может только убывать). Функция Q(t)

Подобный материал:

• Курс лекций "Экспертные системы" (Для студентов заочного обучения юридического факультета, 84.44kb.
• 4 Экспертные системы, 51.16kb.
• 14. Лекция: Позиционно-силовое управление в системе робота-станка, 113.23kb.
• Алгоритмы обучения и архитектура нейронных сетей. Нейросетевые системы обработки информации, 21.42kb.
• Программа дисциплины «Динамические системы» Направление, 73.11kb.
• Рабочая программа дисциплины «Дискретные динамические системы», 110.59kb.
• Говоря простым языком, системы баз знаний это искусство, которое использует достижения, 267.75kb.
• Лекция №15. Экспертные системы Экспертные системы зародились в ходе развития методов, 188.15kb.
• Динамика системы управления гидротурбиной с пидрегулятором, 80.14kb.
• О некоторых особенностях интегрирования обыкновенных дифференциальных уравнений, описывающих, 18.79kb.

^ 49. Цифровая подпись. Системы цифровой подписи на основе криптосистем с открытым ключом.


Схема цифровой подписи.

Существенным недостатком многих электронных систем передачи данных является отсутствие возможности проверки подлинности и авторства пересылаемых документов. Это не позволяет использовать такие системы для заключения юридически признаваемых сделок или для передачи юридически подтверждаемых документов, что часто сводит на нет преимущества таких систем по сравнению с обычной почтовой пересылкой. Как правило, в таких системах полученный документ распечатывается на бумажный носитель, подписывается физическим лицом и удостоверяется печатью юридического лица. Эту проблему можно решить путем использования электронной цифровой подписи, т.е. средства, позволяющего на основе криптографических методов надежно установить авторство и подлинность документа.

Наиболее простой вид цифровой подписи представляет собой так называемый имитоприставка, которая реализуется в виде шифра контрольной суммы по сообщению. В качестве такой контрольной суммы по сообщению может использоваться какое - либо число, отпечаток пальца, и др. Однако в полной мере подлинность и авторство документа устанавливает электронная цифровая подпись, позволяющая заменить при безбумажном документообороте традиционные подпись и печать.

Цифровая подпись зависит от текста заверяемого документа, секретного ключа, доступного только заверяющему лицу, и несекретного общедоступного ключа.

Для реализации схемы цифровой подписи требуется, чтобы преобразования зашифрования Е_K и расшифрования D_K также действовали на пространствах открытых текстов 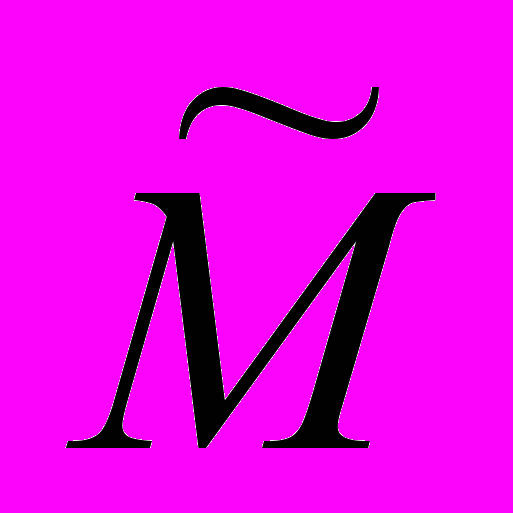и шифротекстов 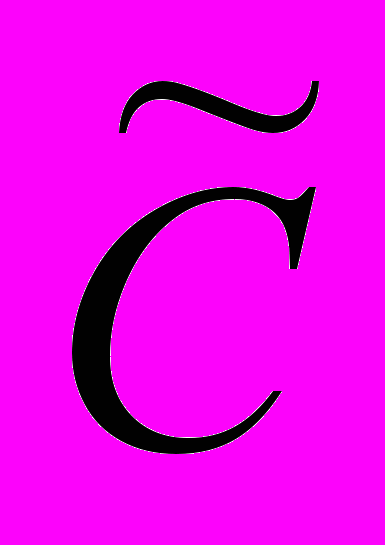и преобразование Е_K было бы обратным преобразованием к D_K , т.е.:

Е_K:

D_K:

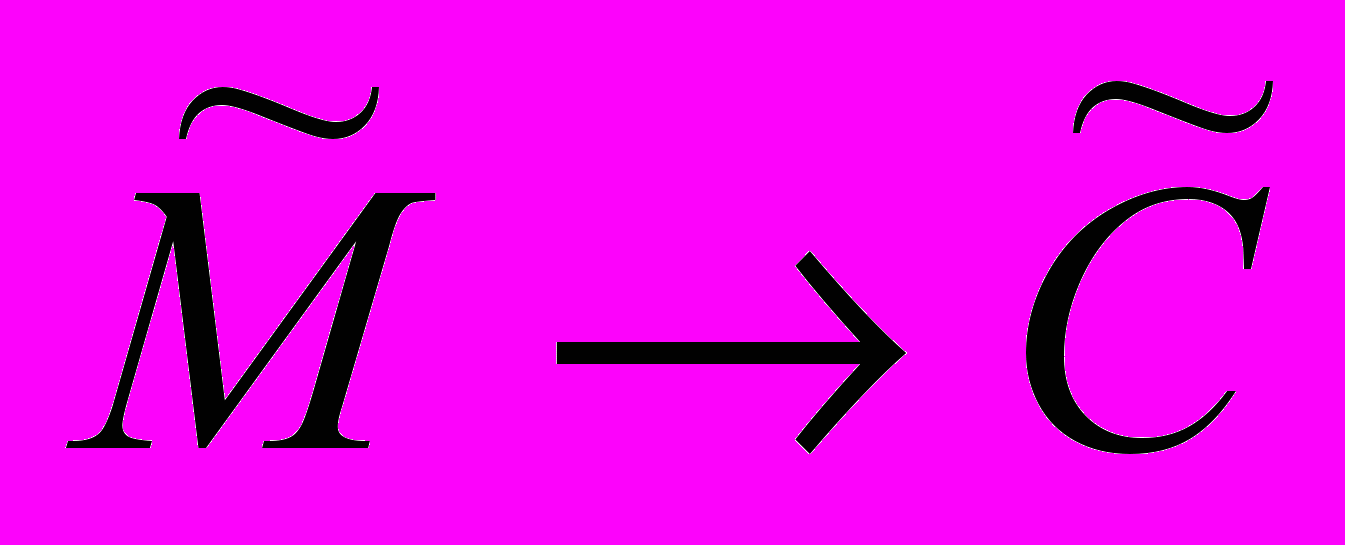
E_K[D_K(M)]=M

для любого открытого текста .

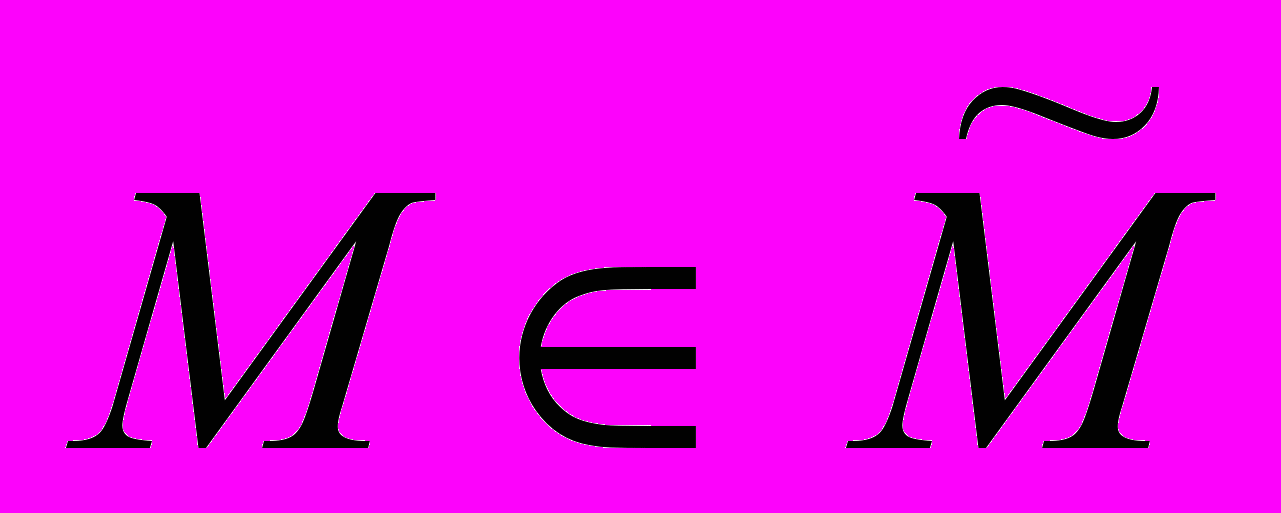Если теперь некоторый пользователь А желает послать сообщение М пользователю В с подтверждением своего авторства, то он может воспользоваться своим секретным ключом, т.е. преобразованием D_K=D_K,A, вычислить величину C=D_K,A[M] и послать это значение (это и будет цифровой подписью) пользователю В. в этом случае преобразование D_K,A используется для шифрования текста М и цифровая подпись обратна алгоритму открытого шифрования. Пользователь В, также как и любой другой пользователь, знающий открытое преобразование E_K,A может убедиться в авторстве сообщения М вычислением этого сообщения из соотношения



и проверкой, является ли М осмысленным текстом. Т.е. здесь E_K,A действуют как преобразование расшифрования.

Авторство пользователя А основано на том, что только он знает секретное преобразование D_K,A . Злоумышленник, желающий подменить сообщение М на другое сообщение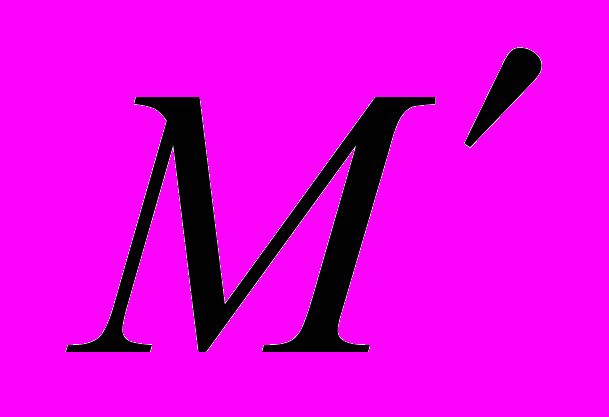, должен решить задачу нахождения такого значения С, что

.

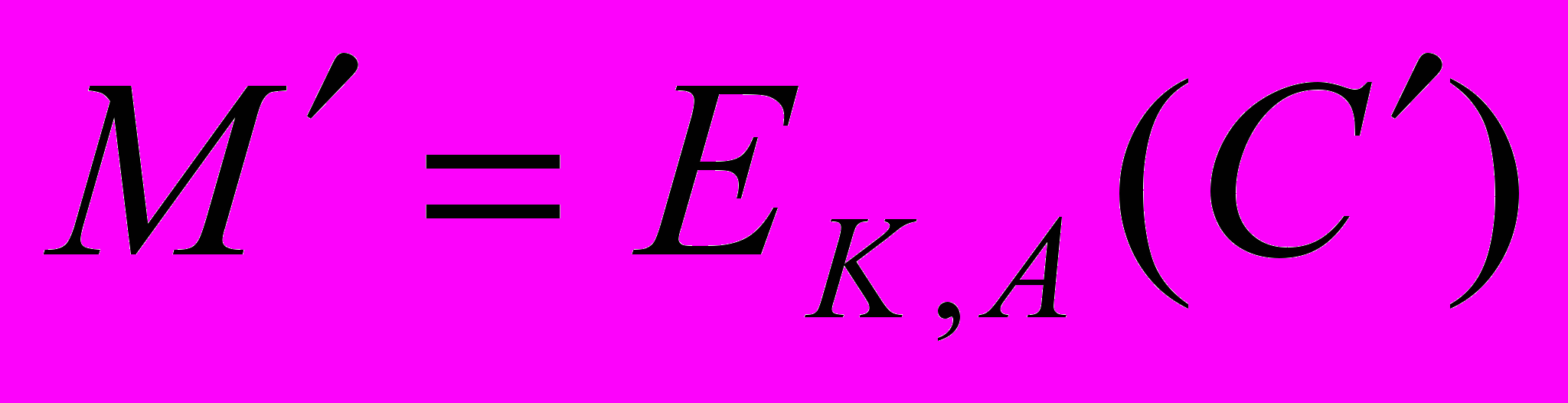В силу односторонней природы (используется односторонняя функция) преобразования сделать это крайне трудно.

Обычно на практике, для сокращения времени подписывания преобразования 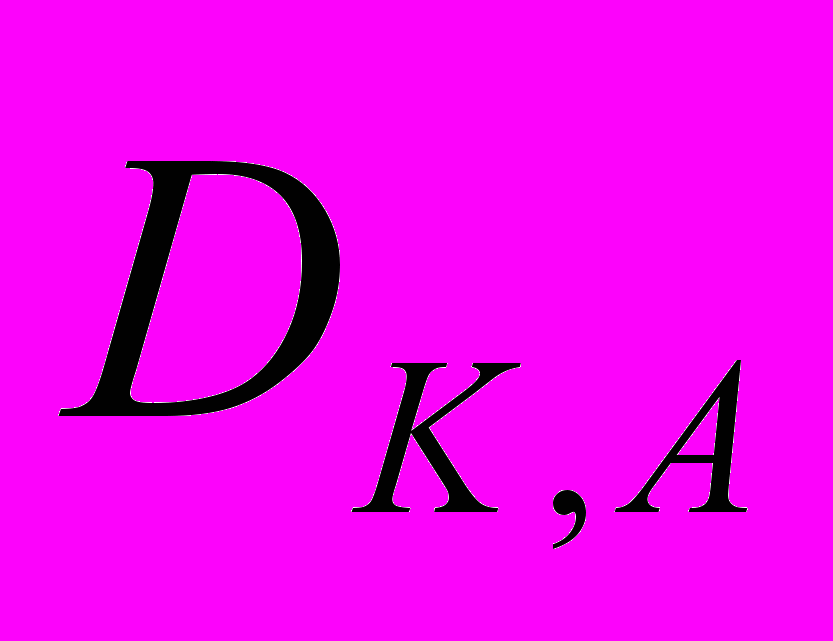применяется не для всего исходного текста М, а для некоторой его хэш-функции H(M) , которая отображает любое сообщение М в сообщение H(M) фиксированного малого размера. Другими словами, цифровая подпись имеет вид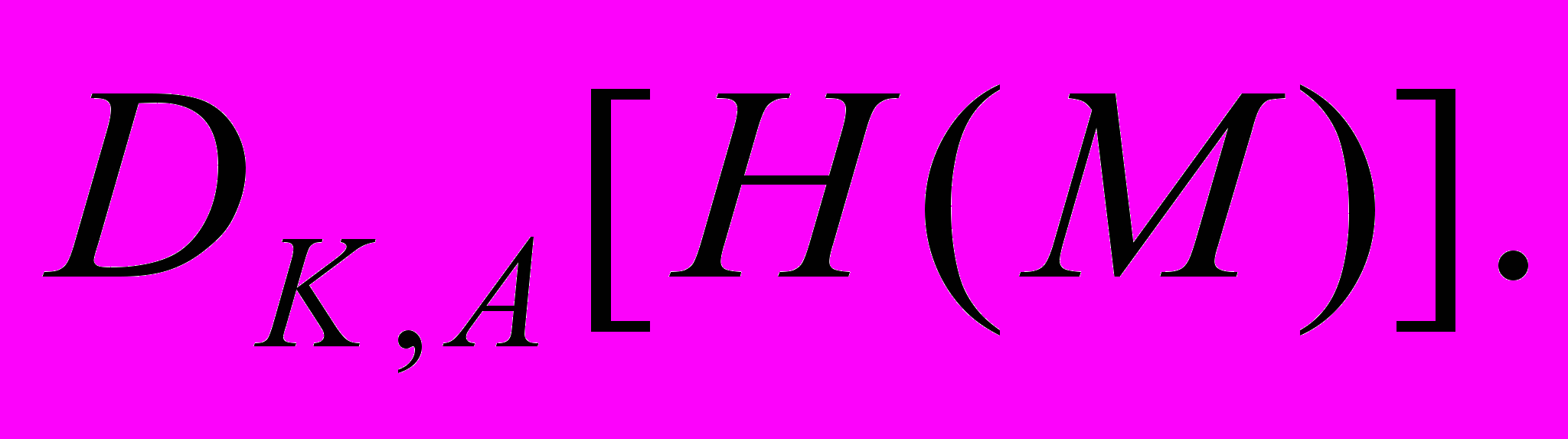



Пользователь В, получив сообщение М и подпись к нему D_K,A может вычислить (функция хэширования общеизвестна) и проверить выполнимость соотношения



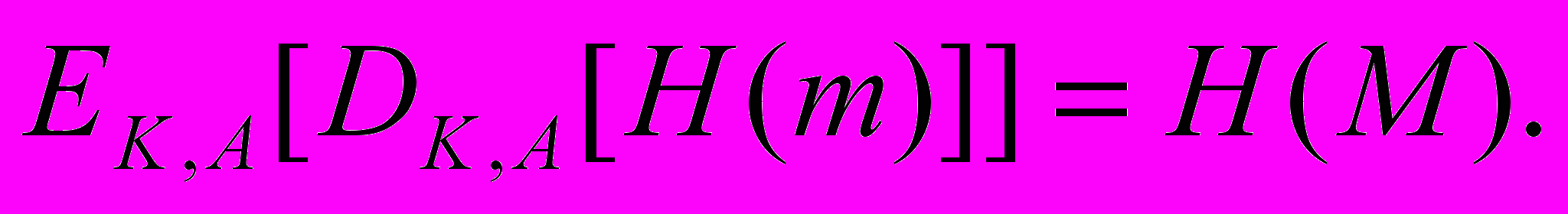
С учетом сказанного, общую схему цифровой подписи может представить следующим образом: схема включает:

1. Пространство открытых сообщений 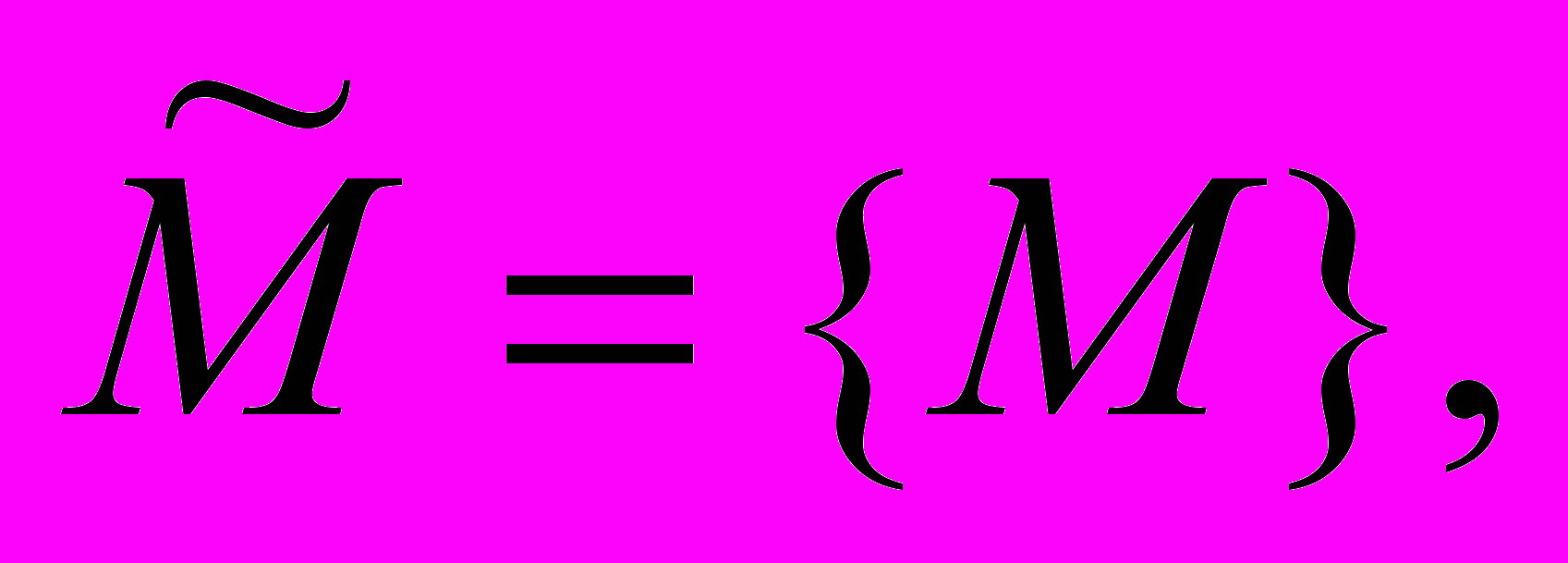к которым применяется алгоритм цифровой подписи.

2. Пространство секретных параметров 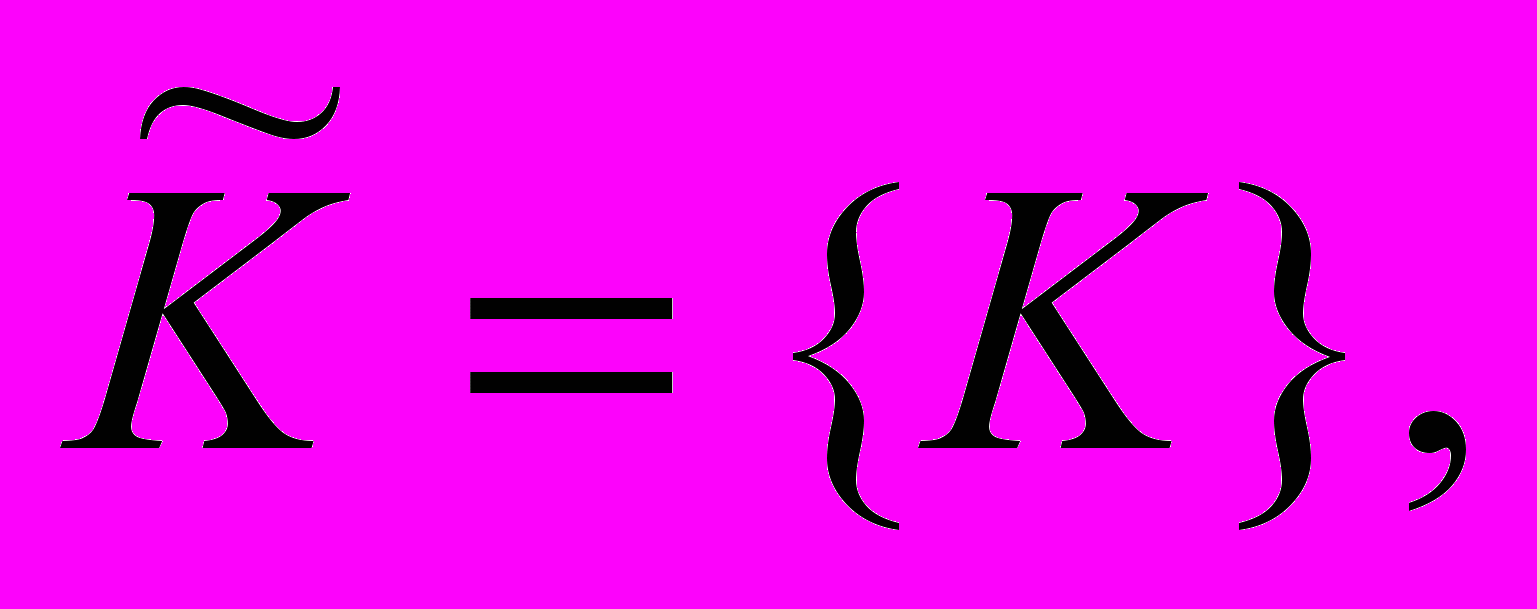которые выбираются пользователем.

3. Алгоритм генерации за полиномиальное время пары (E_K,D_K) - открытого и секретного ключей по выбранному параметру К.

4. Алгоритм подписи Q, который вырабатывает значение Q [М, D_K], называемое цифровой подписью сообщению М.

5. Алгоритм проверки подписи, который проверяет правильность подписи и сообщение с использованием открытого ключа Е_K.

Рассмотрим теперь конкретный алгоритм цифровой подписи, предложенный Эль Гамалем (1985)

Все пользователи знают большое простое число и примитивный элемент 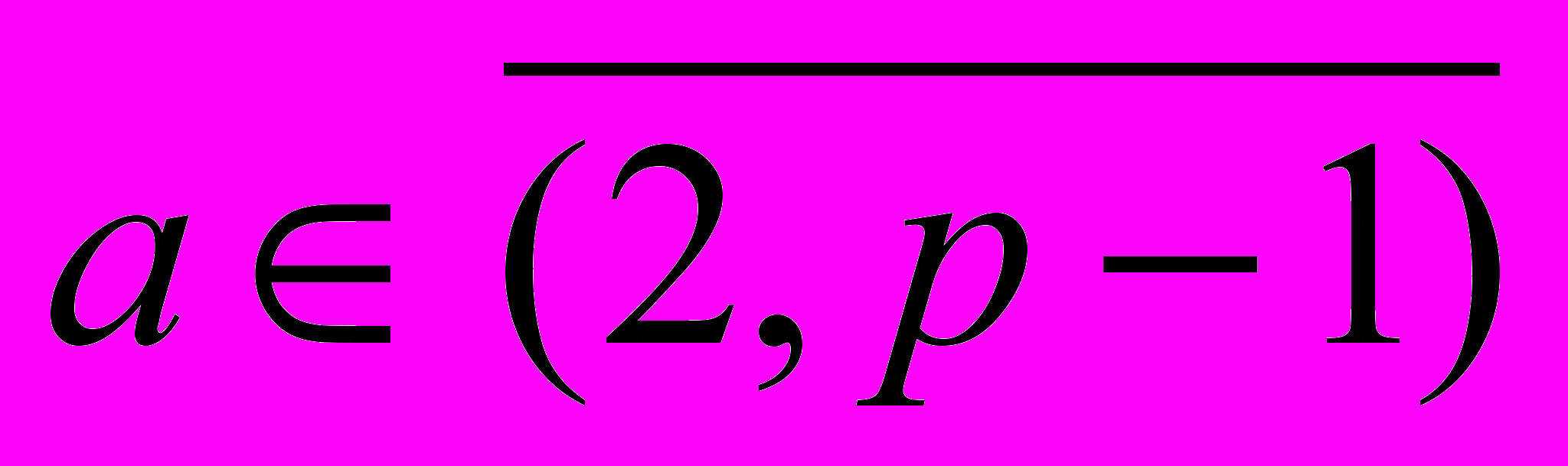по модулю Р. Секретная информация подписывающего пользователя А состоит из двух частей:

1. 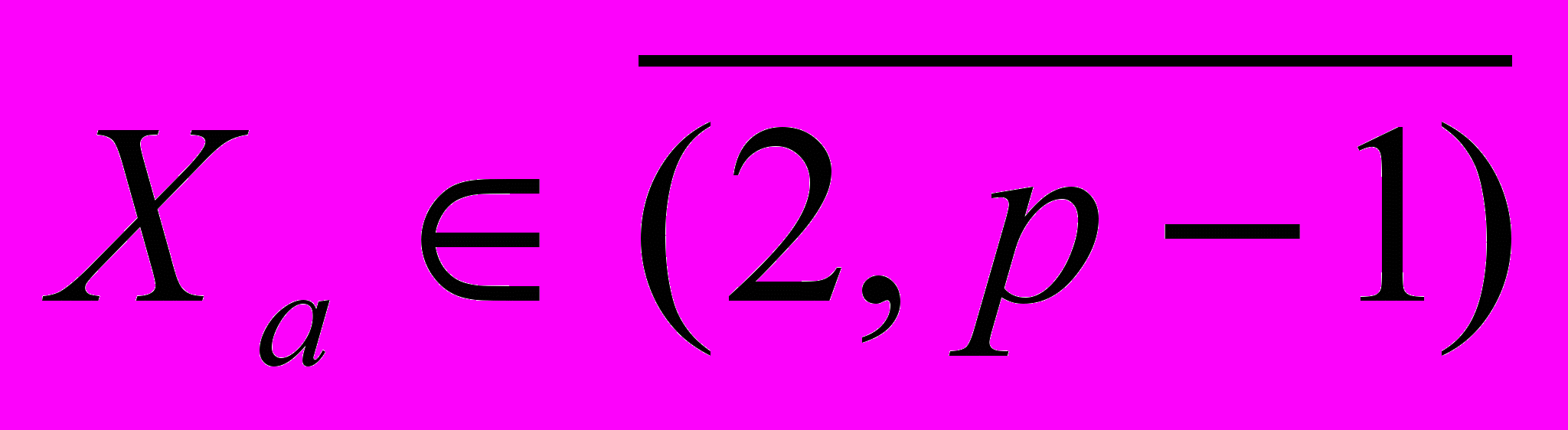- долговременный секретный ключ подписи выбирается случайно из интервала и хранится в секрете.

2. 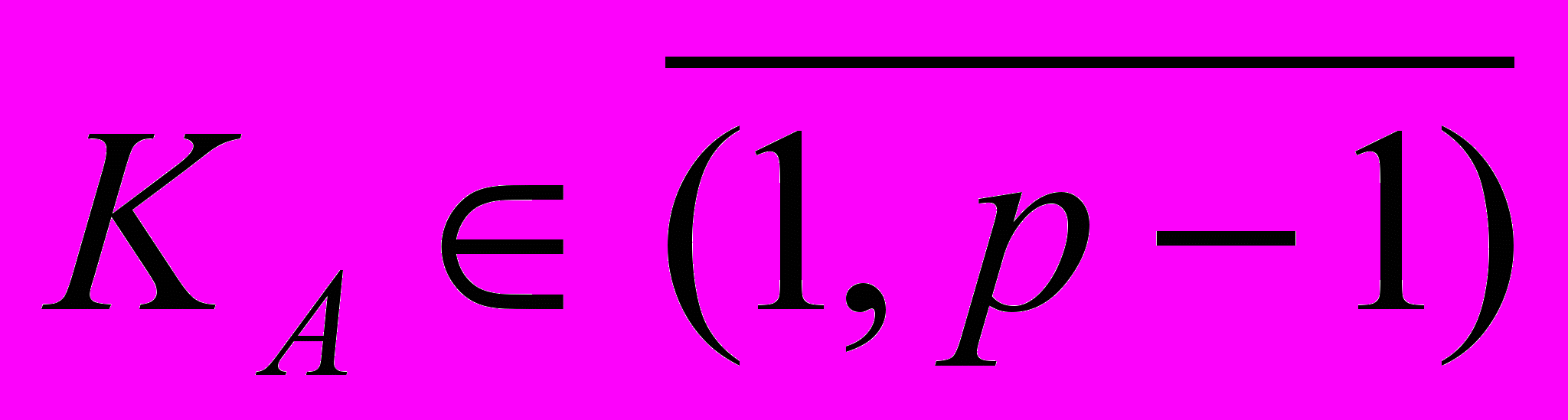- разовый секретный ключ подписи конкретного сообщения, такой что , т.е. взаимно просто с p -1.

Открытая информация подписывающего тоже имеет 2 части:

1. 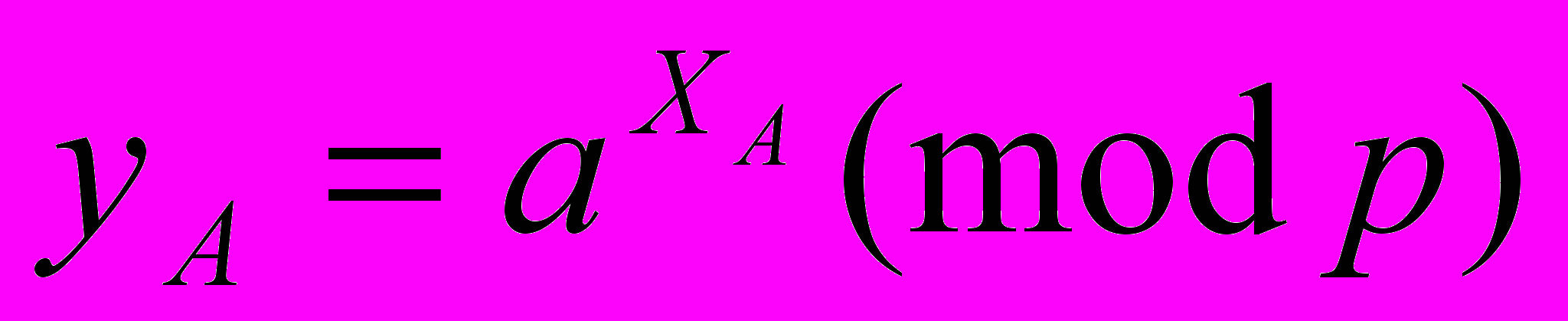- открытый ключ подписи.

2. 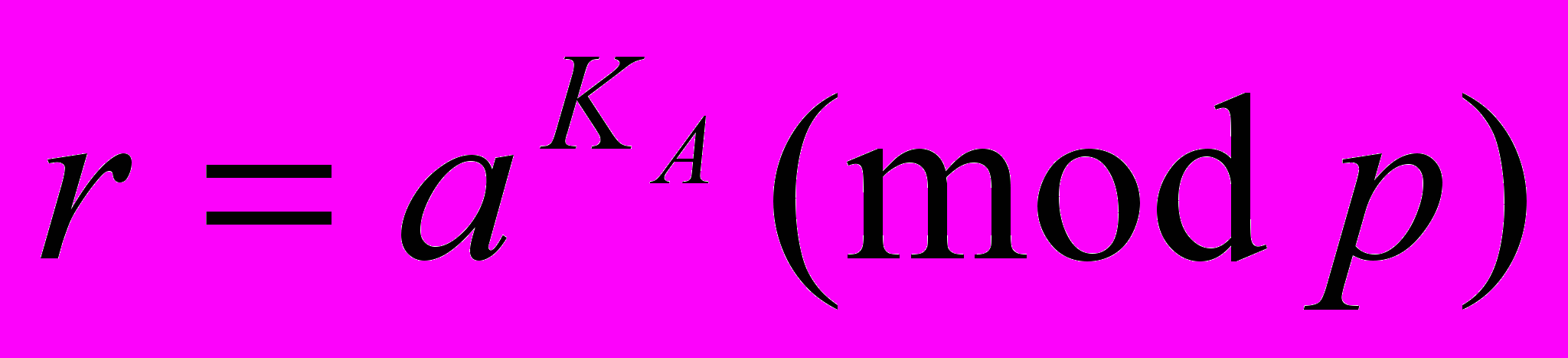- первая из двух частей подписи (r,s).

Подписываемое сообщение представляется числом из интервала (0,p -1) точнее его функцией хэширования H(M).


АЛГОРИТМ ПОДПИСИ СООБЩЕНИЯ М:

1. Пользователь А выбирает случайное число из интервала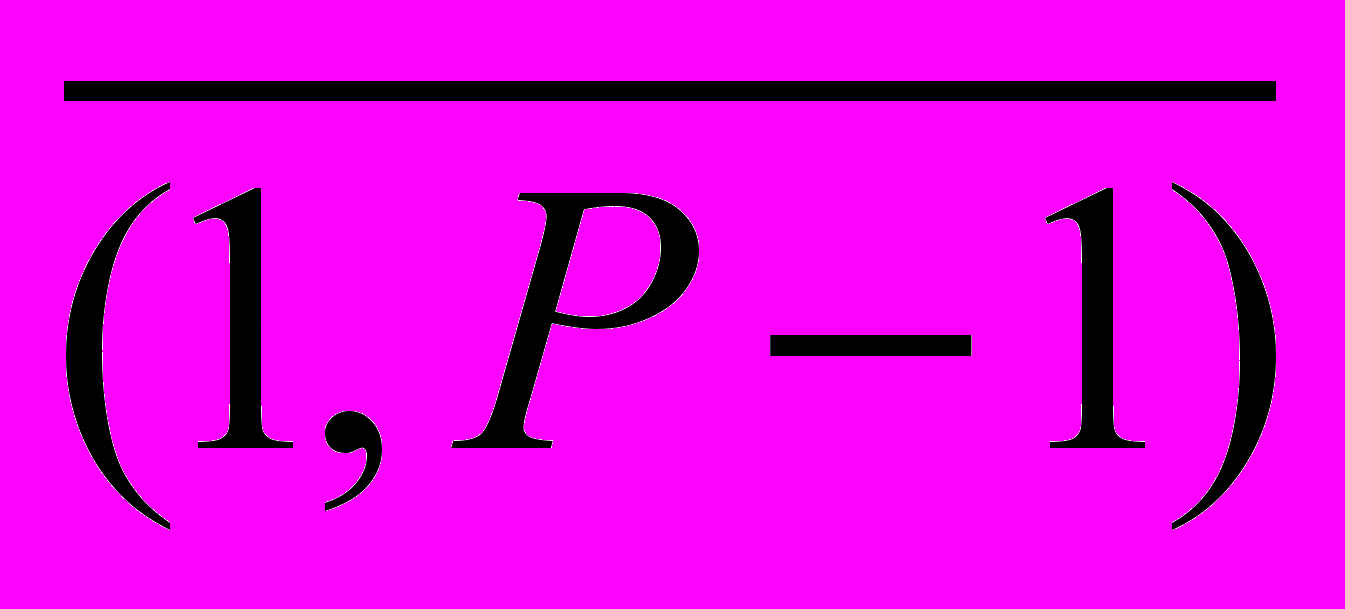, таким образом, чтобы НОД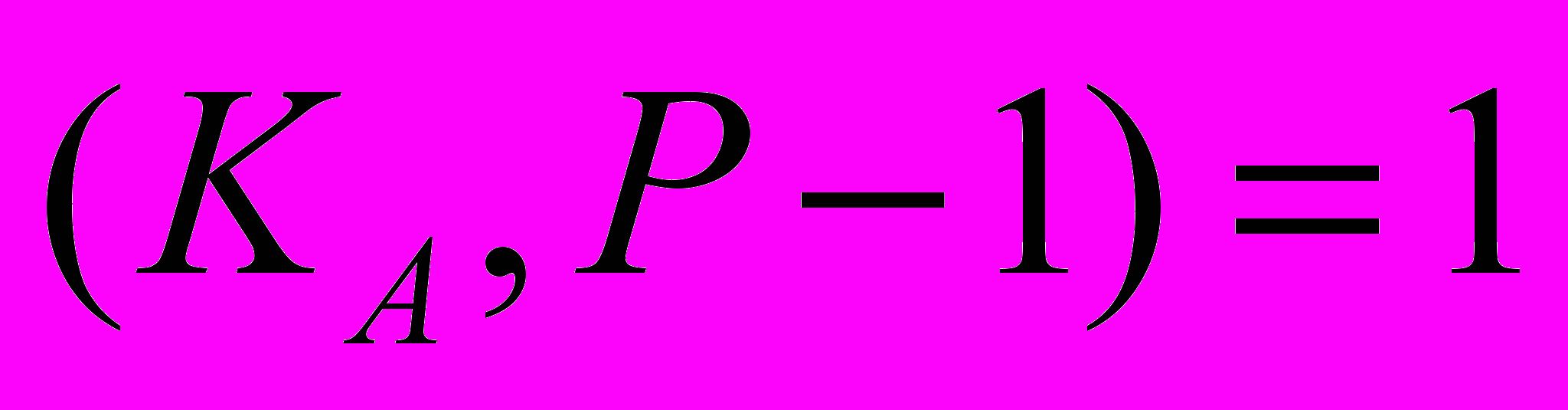

2. Вычисляет т.е. число удовлетворяющее сравнению 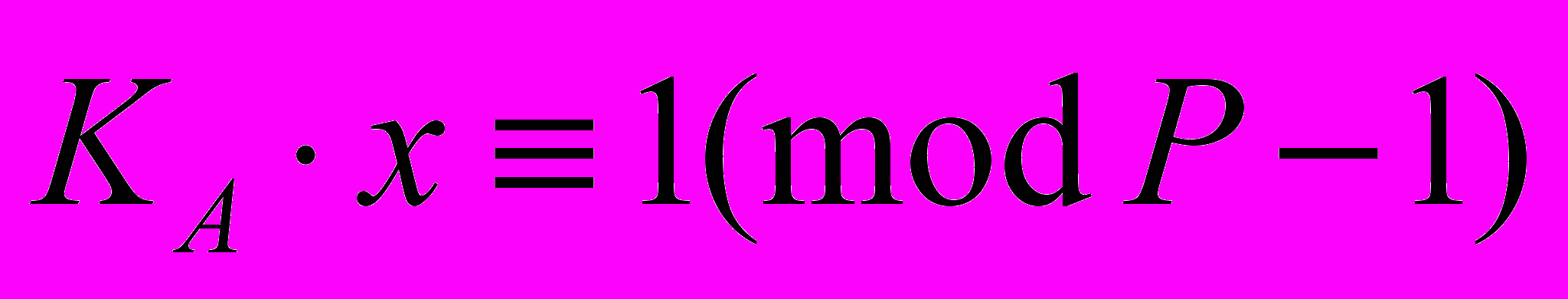Именно для разрешимости этого сравнения при выборе 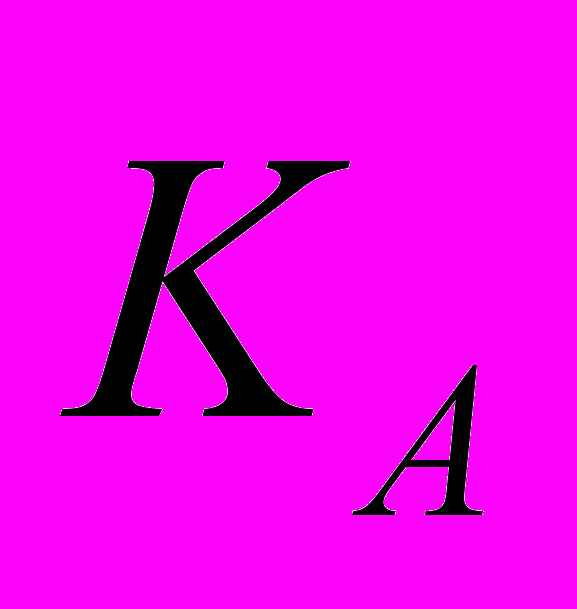наложено условие его простоты, с.

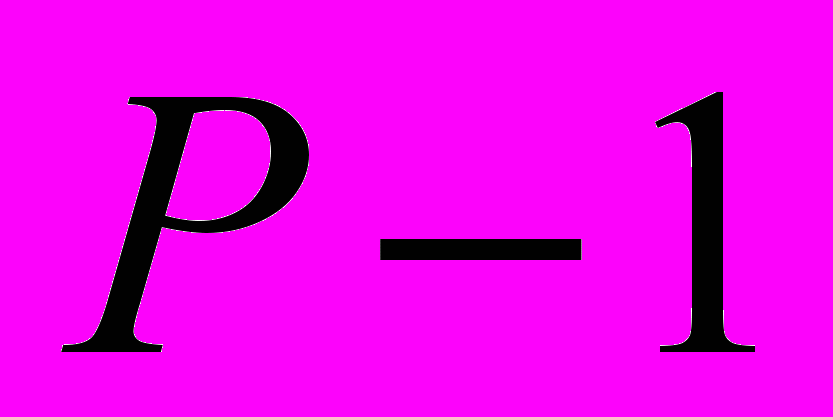3. Вычисляем первую часть подписи .

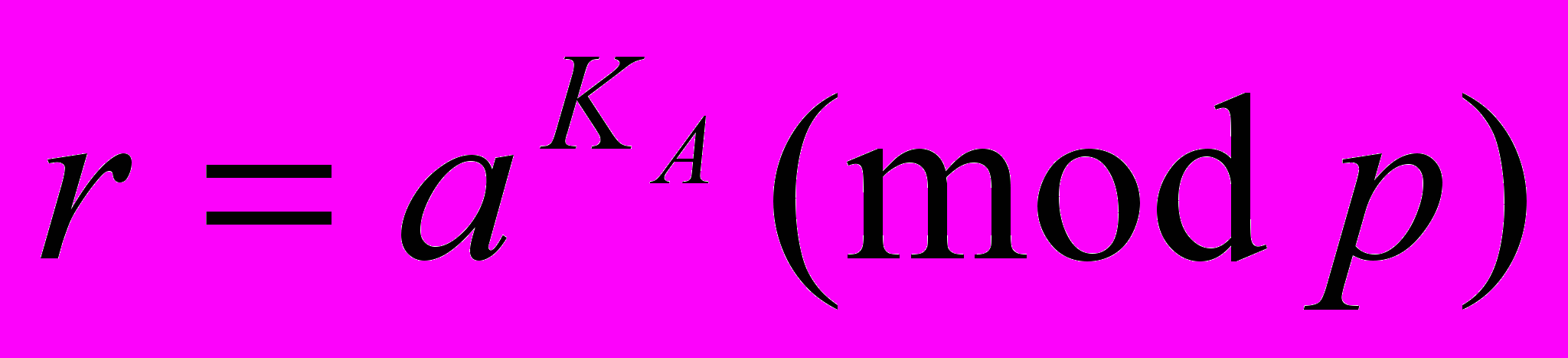4. Вычисляем вторую часть подписи по формуле .

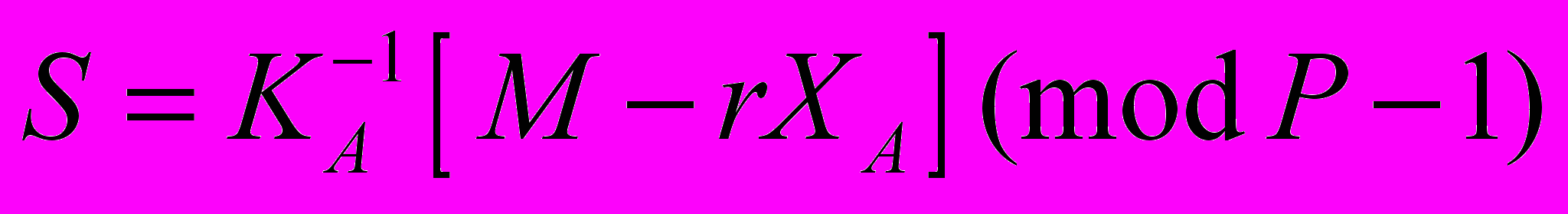На этом процедура выработки подписи (r,S) к сообщению М заканчивается, и эти данные M,r,S сообщаются получателям.


АЛГОРИТМ ПРОВЕРКИ ПОДПИСИ К СООБЩЕНИЮ М

По полученным данным M, r, S и имеющемуся у получателя открытому ключу отправителя y_A вычисляются величины и В случае выполнения равенства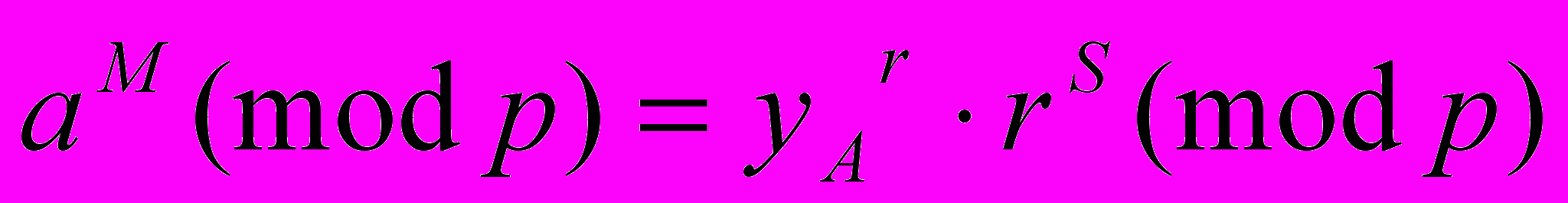



считается, что подпись верная.

Поясним работу алгоритмов. Рассмотрим проверяемое равенство 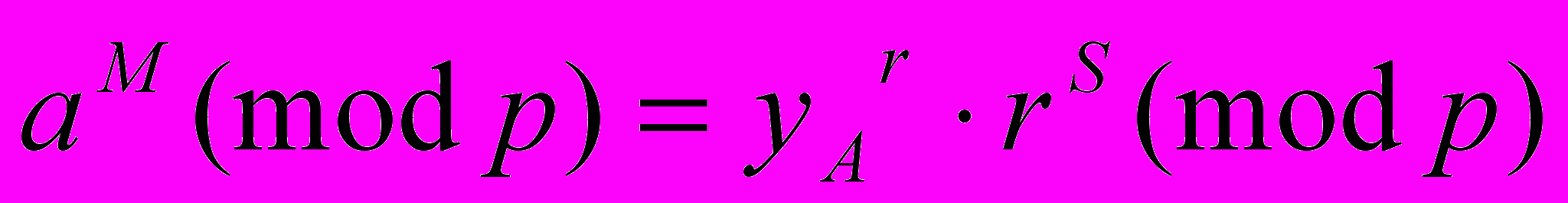или сравнение 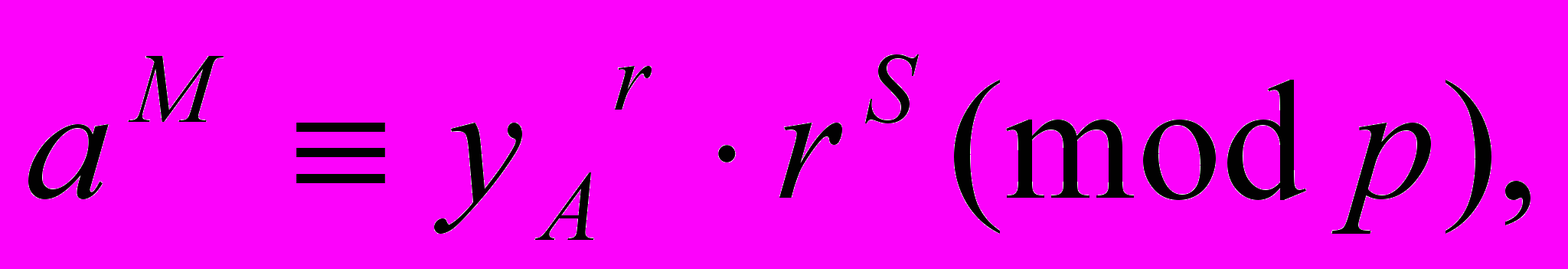решением которого и является числа r и s. После подстановки y_A и r оно примет вид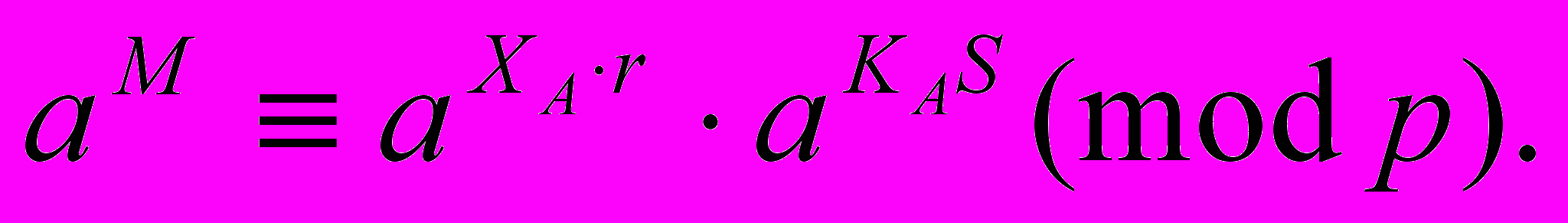



Учитывая свойства сравнений (теорема Эйлера - Ферма), последнее эквивалентно сравнение по модулю (Р – 1) вида:



Именно из этого сравнения подписывающий пользователь вычисляет величину



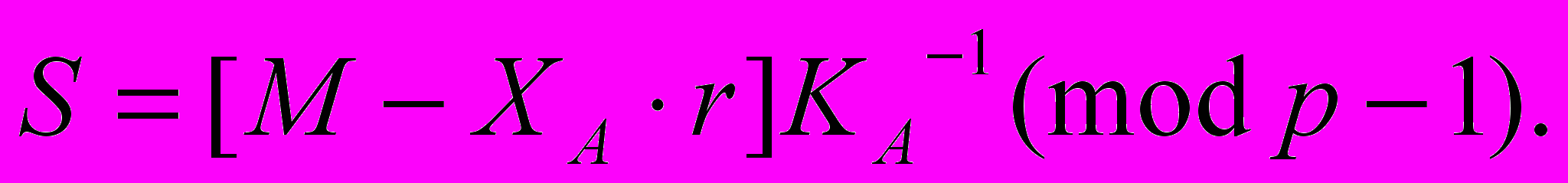
Особенностью алгоритмов цифровой подписи является наличие у подписывающего абонента секретного ключа . При этом, в случае проверки, он предъявляет контролеру не сам секретный элемент, а некоторые значение функции, вычисляемое с помощью секретного ключа по случайному запросу контролера, доказывая тем самым, что он обладает секретом, путем его косвенной демонстрации, путем вычислений. Именно отсюда появилось название «доказательство при нулевом знании», которое получил протокол общения абонентов, когда абонент доказывает, что он обладает секретом, не раскрывая самого секрета. Алгоритмы «доказательства при нулевом знании» не являются собственно криптографическими, т.к. они служат для передачи сообщений типа « я знаю эту информацию». Однако, такие алгоритмы совместно с алгоритмами цифровой подписи, шифрования с открытым ключом и открытого распределения ключей позволяют организовывать более совершенные протоколы взаимодействия пользователей криптографической сети, которые реализуют одновременно и подтверждение подлинности документов и доказательство при нулевом знании.

Общая идея алгоритмов доказательства при нулевом знании состоит в том, что он может вычислять некоторую функцию, зависящую от секретного ключа и от аргументов, задаваемых проверяющим. Проверяющий, даже зная эти аргументы, не может по данному ему значению функции восстановить секретный ключ. При этом функция должна быть такой, чтобы проверяющий мог удостовериться в правильности ее вычисления, например, эта функция может представлять собой цифровую подпись выбранных им аргументов.

Рассмотрим алгоритм доказательства при нулевом знании, в основе которого лежит описанный ранее алгоритм RSA:

1. Доказывающий А и контролер В, оба знают идентификатор I и открытый ключ n, e, но А, кроме того, знает еще секретное число 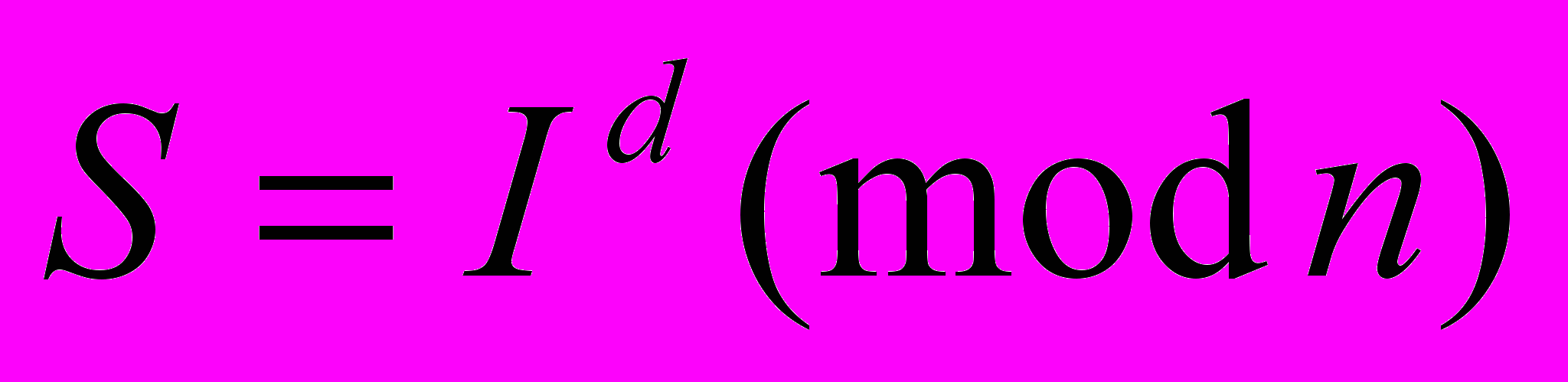, сформированное по секретному ключу d. Сначала А генерирует случайное число Х и вычисляет 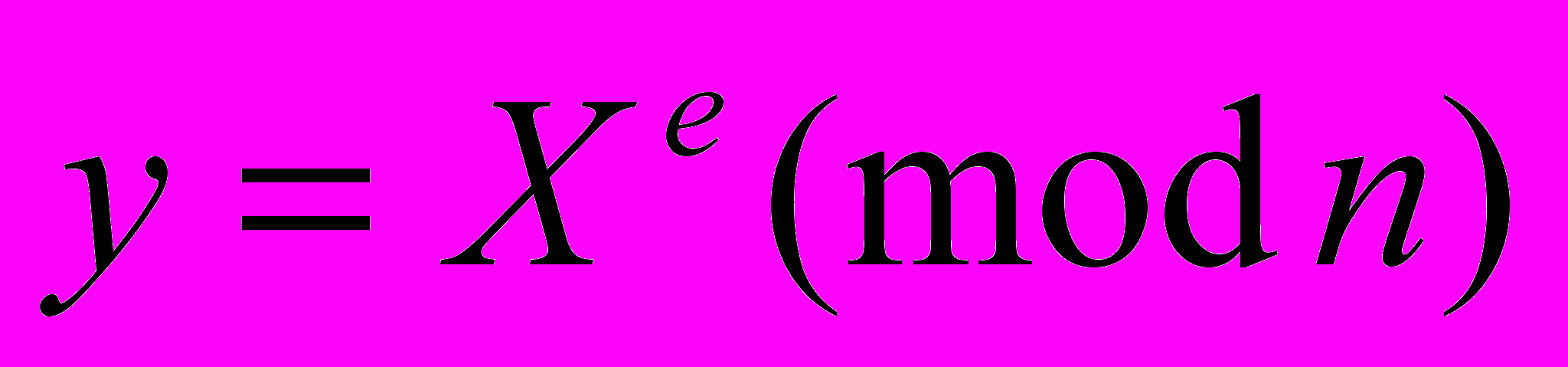. Затем он отсылает I,y к B.

2. После этого В генерирует и передает А случайное число V.

3. Затем А вычисляет и передает В число



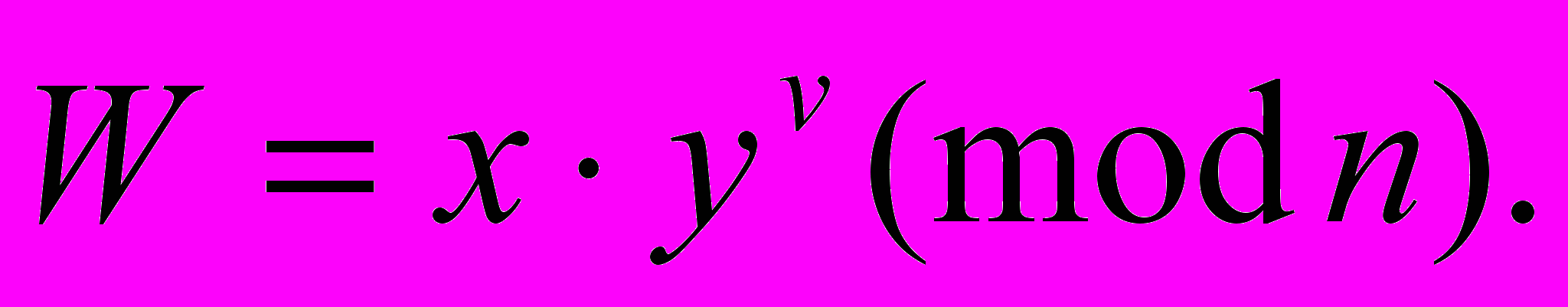
4. Контролер В проверяет принадлежность идентификатора I к А путем проверки тождества




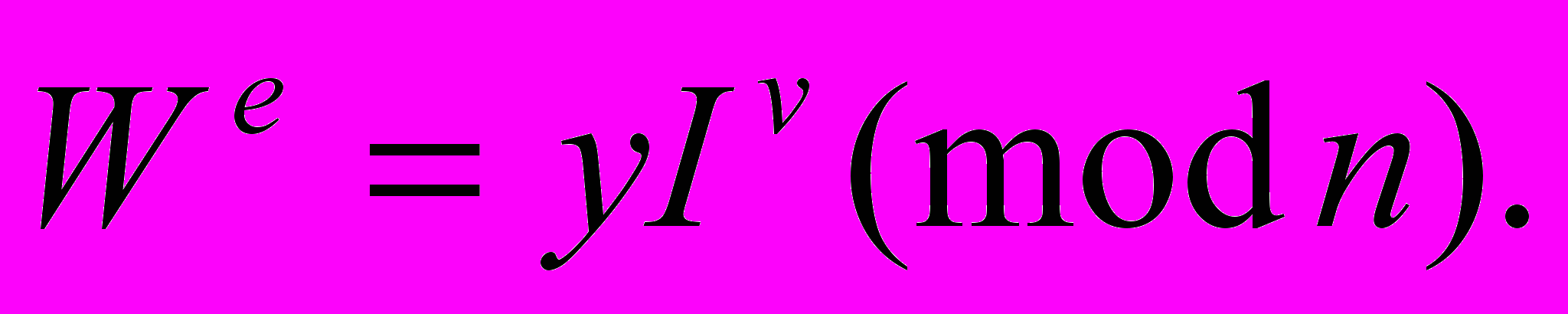
^ 50. Хэш-функции. Использование хэш-функций в системах цифровой подписи.


Хэш-функции – алгоритм, который превращает сообщение любой длины в сообщение определенной длины.

Значение h=H(M’) зависит от каждого бита сообщения М.

H(M’)=h

Нет одного h соответствующего нескольким М.

Хеш-функции.

Термин хеш-функция (или функция хеширования) возник в теории сложности вычислений, где он обозначал функцию, которая сжимает строку чисел произвольного размера в строку чисел фиксированного размера. Это понятие использовалось в алгоритмах поиска данных по значениям хеш-функции от них. Рассмотрим это понятие применительно к криптографии.

Криптографические хеш-функции делятся на два класса: с ключом и без ключа. Значение хеш-функции с ключом может вычислить лишь тот, кто знает некоторый секретный параметр - ключ. В литературе она еще называется МАС - кодами аутентификации сообщений.

Определение. Хеш-функцией с ключом (зависящей от ключа) называется функция, имеющая следующие свойства:

1. Описание функции Н(k,x) должно быть открыто, а секретная информация должна содержаться только в выборе ключа k (правило Керкхофа).

2. Аргумент х функции Н(k,x) может быть строкой чисел произвольной длины, а значение функции должно быть строкой чисел фиксированной длины.

3. При любых данных k и х вычисление Н(k,x) должно быть быстрым (за полиномиальное время)

4. По любому данному х должно быть трудно угадать значение Н(k,x) с вероятностью большей, чем 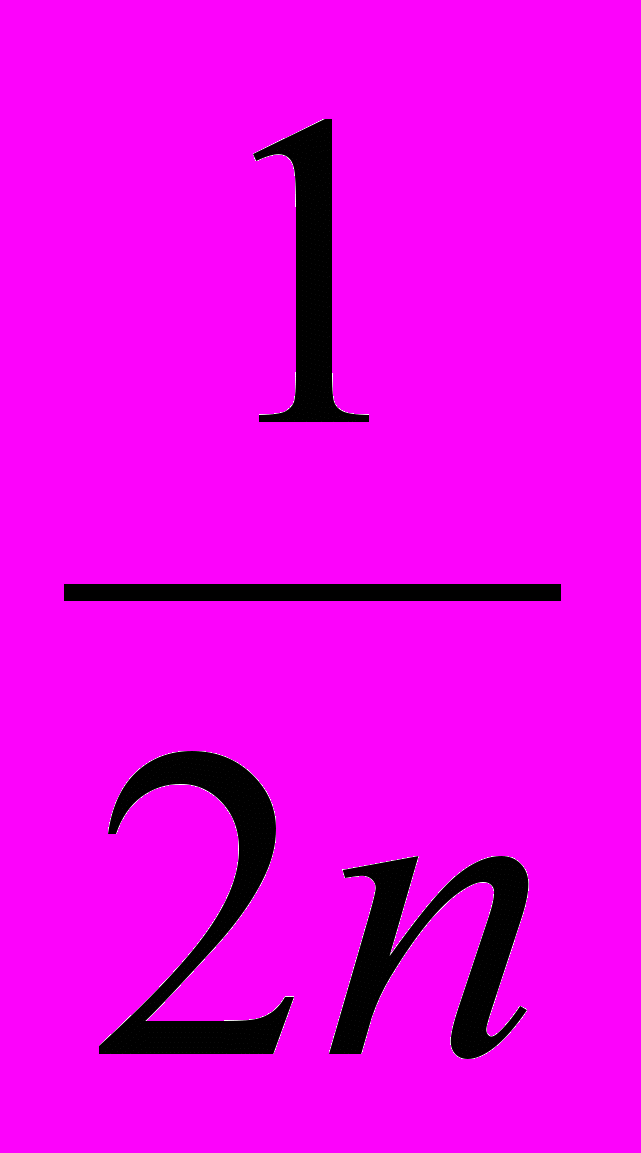, где n - число бит в выходной строке. Должно быть трудно определить ключ k даже по большему числу известных пар 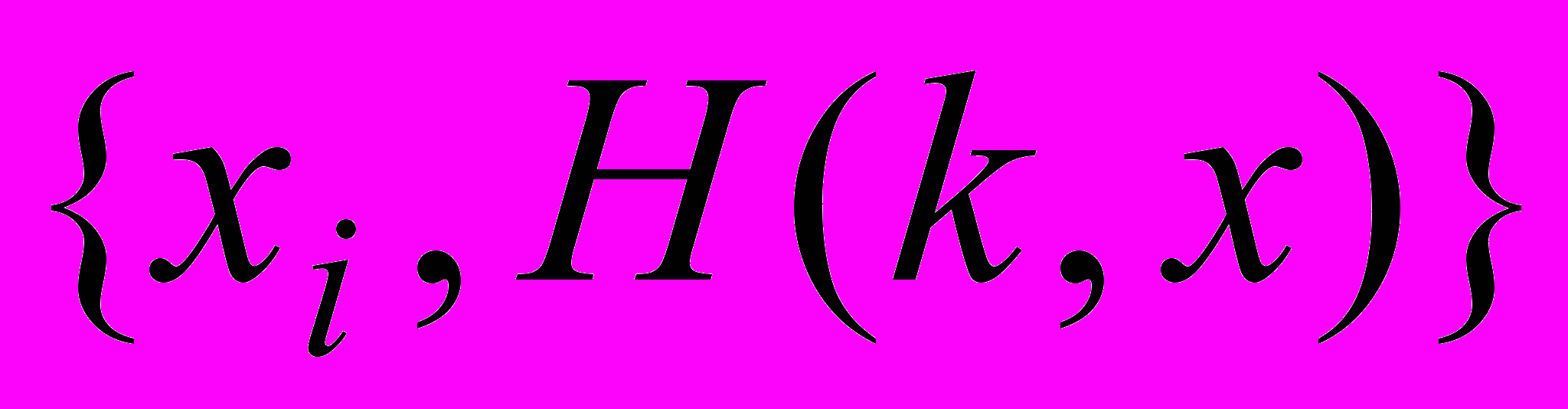или вычислить по этой информации Н(k,x’)для x’x_i.

Хеш-функция без ключа называется МДС - код определения манипуляции. Эти функции делятся на два класса: слабые односторонние хеш-функции и сильные односторонние хеш-функции.

Определение. Односторонней слабой хеш-функцией называется функции Н(х), удовлетворяющая условием:

1. Аргумент х функции может быть строкой чисел произвольного размера

2. Значение функции Н(х) представляет собой строкой фиксированного размера

3. Значение функции Н(х) легко вычисляется (за полиномиальное время)

4. Почти для всех y вычислительно невозможно найти такое х что Н(х)=y

5. Для любого фиксированного х вычислительно невозможно найти другое x’x такое, что 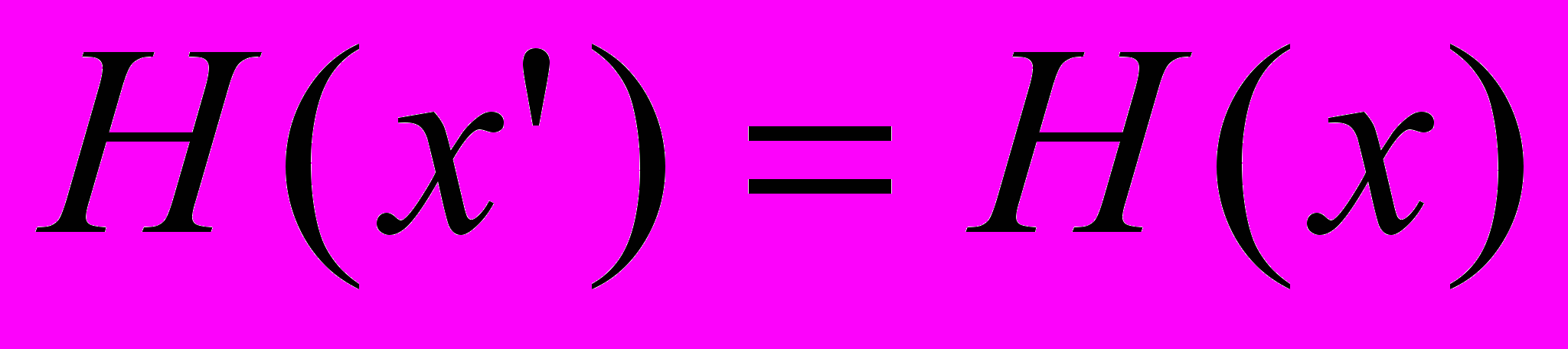. Такое событие, т.е. 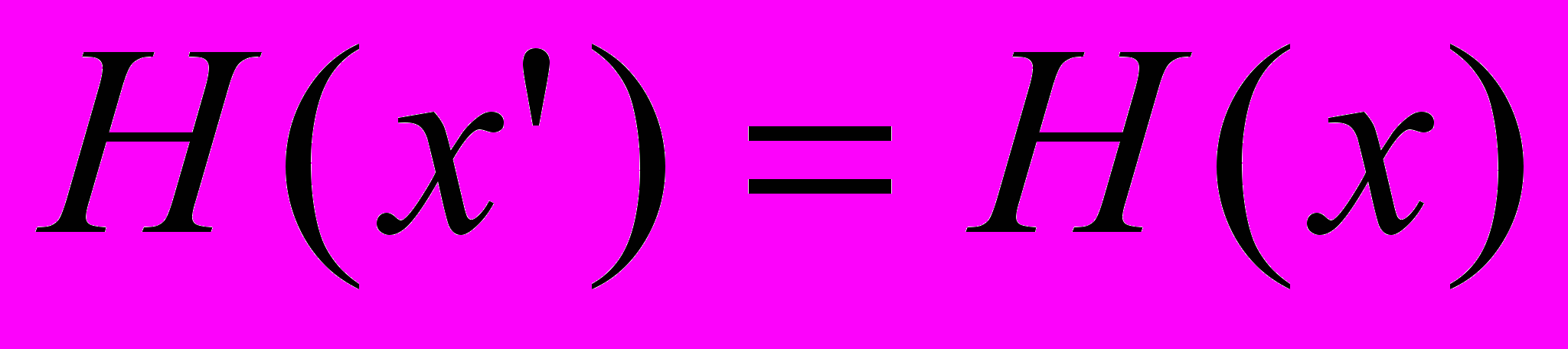называется коллизией.

Свойства 3 и 4 утверждают, что 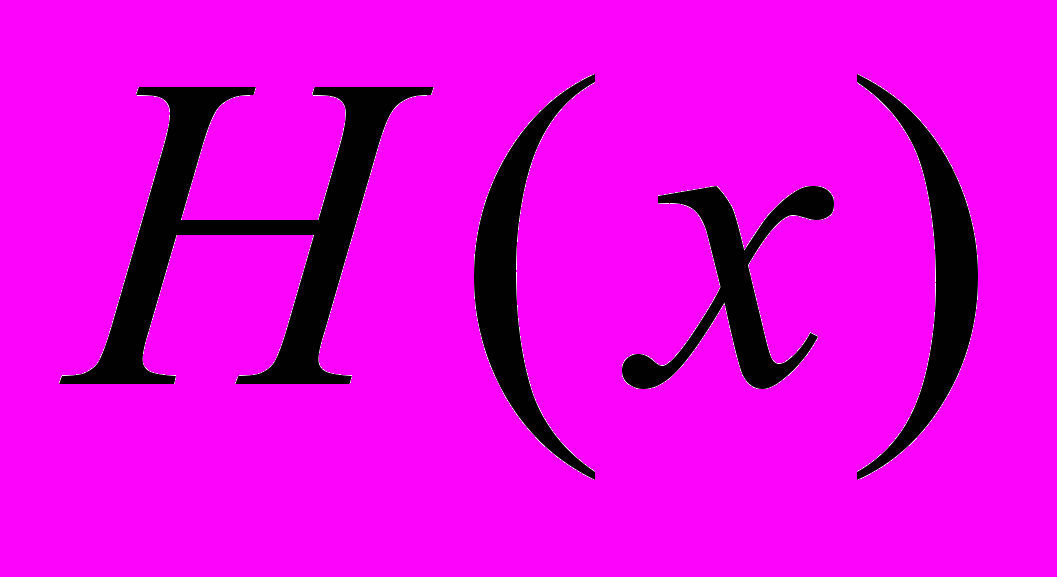является односторонней функцией. По свойствам 1 и 2 коллизии должны существовать, однако свойство (5) требует, чтобы найти их было вычислительно невозможно.

Определение. Односторонней сильной хеш-функцией 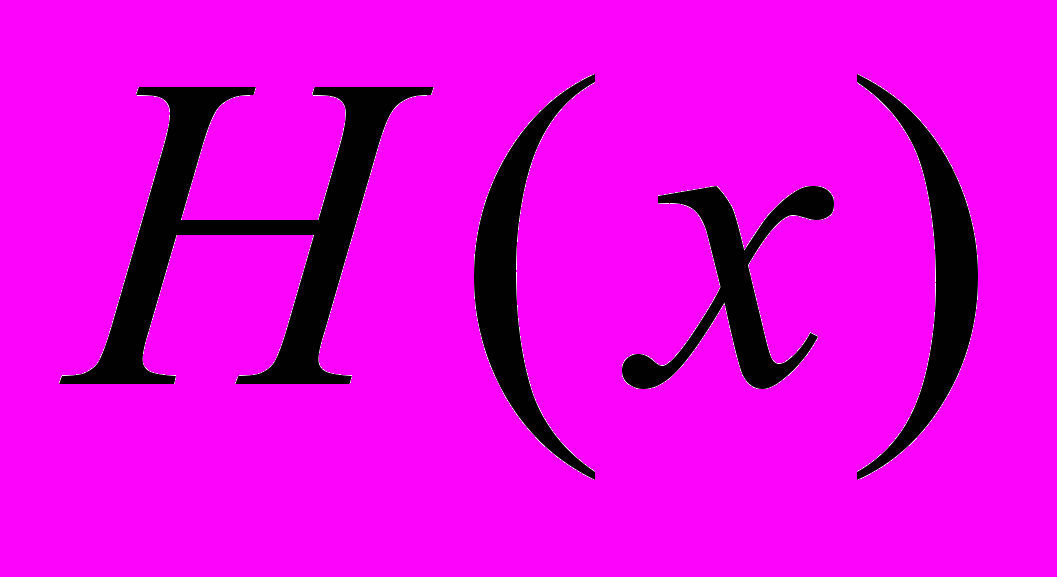является функция, удовлетворяющая свойством 1 - 4 предыдущего определения, а свойств 5 заменяется следующим.

5. Вычислительно невозможно найти любую пару аргументов 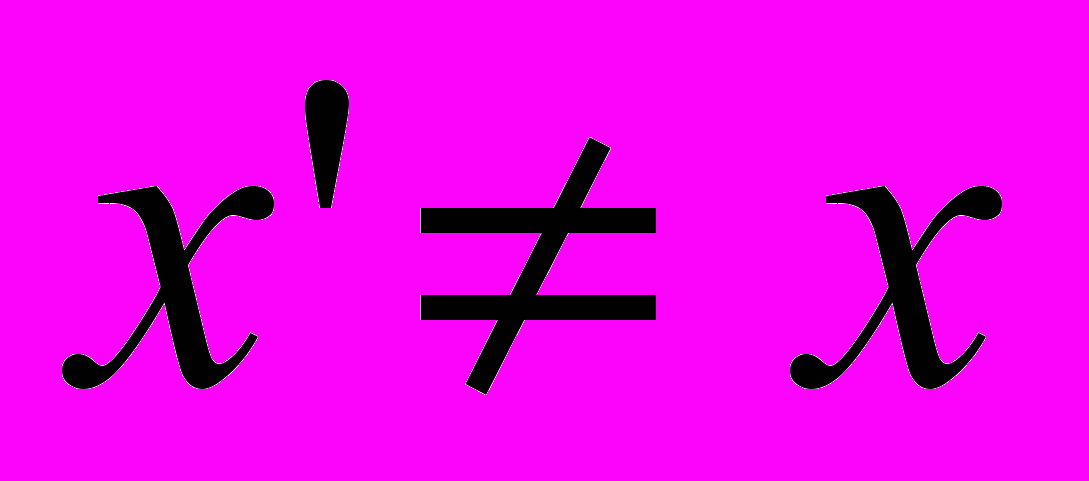такую, что 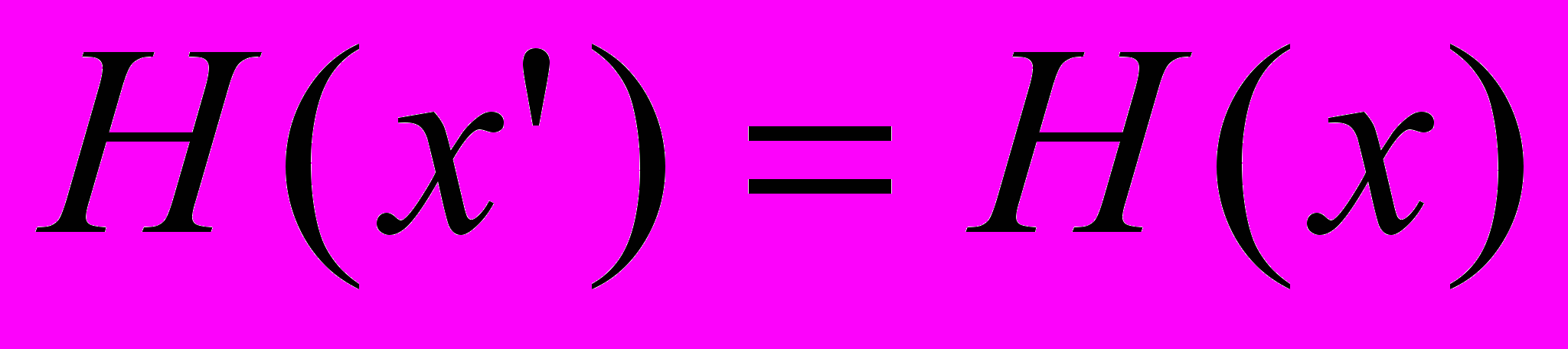. Оба определения предполагают выполнение правила Керкхофа , т.е. описание функции 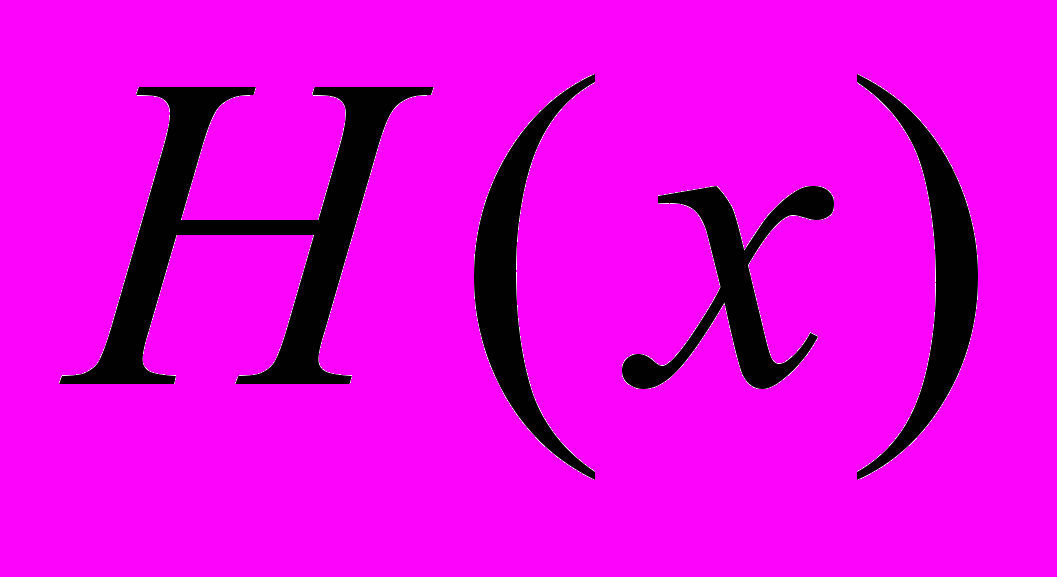открыто.

Применение криптографических хеш-функций исключительно разнообразно и одним из основных их применений являются схемы и алгоритмы цифровой подписи сообщений. Об этом мы поговорим ниже.


^ 51. Показатели надежности систем без восстановления и с восстановлением.


Показатели безотказной работы.


Вероятность безотказной работы P(t) —вероятность того, что в заданном интервале времени t в изделии не возникнет отказа, т. е. 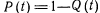, где ^ Q(t) —вероятность появле­ния отказа щ течение времени i.

Очевидно, что ; 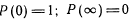. Функция ^ P(t) монотонно убывающая (в процессе эксплуатации или хранения надежность может только убывать). Функция Q(t) монотонно возрастающая.

Для определения величины Р (t) применяется статистичес­кая оценка



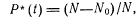
где N, N_o — число изделий, доставляемых на испытания (экс­плуатацию) и отказавших в течение времени t.

Вероятность безебойной работы Р_сб(0—вероятность то­го, что в заданном интервале времени t будет отсутствовать сбой в изделии



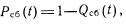
где Q_C6{t) —функция распределения сбоев в течение време­ни t. Для определения статистической оценки справедливо соотношение



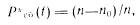
где п, п₀— число изделий соответственно, поставляемых на испытания (эксплуатацию) и, у которых произошел сбой и течение времени /.

Интенсивность отказов λ(t) —условная плотность вероят­ности возникновения отказа невосстанавливаемого объекта, определенная для рассмотренного'момента времени при ус­ловии, что до этого момента отказ не возник Для нахож­дения Я (О используется статистическая оценка



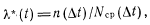
где —число отказавших изделий и среднее число исправно работающих изделий в интервале времени At Средняя наработка до отказа (среднее время безотказной работы) Т представляет собой математическое ожидание до первого отказа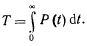



Средняя наработка до отказа вычисляется посредством статистической оценки



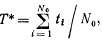
где ti — время безотказной работы t-ro изделия.

Показатели ремонтопригодности.

Вероятность восстановления S(t) — вероятность того, что отказавшее изделие будет восстановлено в течение заданного времени t.

Для расчета S(t) используется статистическая оценка



где п_в, Nob — число изделий соответственно, время восстанов­ления которых было меньше заданного времени t и постав­ленных на восстановление.

Интенсивность восстановления µ{t) —условная плотность распределения времени восстановления для момента време­ни / при условии, что до этого момента восстановление из­делия не произошло.

Для определения \i{t) применима статистическая оценка

где п — число восстановленных изделий за время 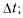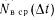—среднее число изделий, которые не были восста­новлены в интервале времени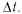

Среднее время восстановления 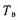— представляет собой математическое ожидание -времени восстановления



Величина Т_в статистически определяется из соотношения




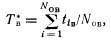
Где 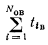сумма промежутков времени, затраченная на обнаружение и устранение отказов; —число восстанов­ленных отказов (равно числу отказов).