40. Динамические экспертные системы

Вид материала

Документы

Содержание Si величина случайная, имеющая свое рас­пределение Pi{t) —работоспо­собность; —отказ; к 55. Методы приближенной оценки надежности цифровых устройств. А и Б одинакова; при k А позволяет получить более высокую достоверность работы. Однако использование тестового контроля по варианту А

Подобный материал:

• Курс лекций "Экспертные системы" (Для студентов заочного обучения юридического факультета, 84.44kb.
• 4 Экспертные системы, 51.16kb.
• 14. Лекция: Позиционно-силовое управление в системе робота-станка, 113.23kb.
• Алгоритмы обучения и архитектура нейронных сетей. Нейросетевые системы обработки информации, 21.42kb.
• Программа дисциплины «Динамические системы» Направление, 73.11kb.
• Рабочая программа дисциплины «Дискретные динамические системы», 110.59kb.
• Говоря простым языком, системы баз знаний это искусство, которое использует достижения, 267.75kb.
• Лекция №15. Экспертные системы Экспертные системы зародились в ходе развития методов, 188.15kb.
• Динамика системы управления гидротурбиной с пидрегулятором, 80.14kb.
• О некоторых особенностях интегрирования обыкновенных дифференциальных уравнений, описывающих, 18.79kb.

Рассмотрим еще один пример. Рассчитаем вероятность безотказной работы схемы с мажоритарным резервированием (см. рис. 8). Предположим, что надежность мажоритарного органа равна единице.

Составляем таблицу истинности (табл. 2)



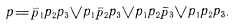
Булева функция р задана ОДНФ. Непосредственно пере­ходим к замещению булевой функции вероятностной



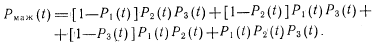
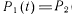
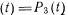
Так как 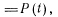то.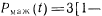

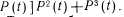При .

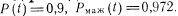Таким образом, логико-вероятностный метод позволяет проводить точный расчет надежности систем, каждой из эле­ментов которой имеют два состояния полной работоспособ­ности и отказа.

Таблица 2

№ п/п	P1	Р2	P3	р
1	0	0	0	0
2	0	0	1	0
3	0	1	0	0
4	0	1	1	1
5	1	0	0	0
6	1	0	1	1
7	1	1	0	1
8	1	1	1	1

Логико-вероятностный метод, основанный на булевой мо­дели надежности системы, не позволяет учитывать очеред­ность наступления отказов. Для учета очередности исполь­зуется последовательное дерево отказов [3].

Для оценки надежности изделия, подвергающегося техни­ческому обслуживанию, используют математический аппа­рат марковских процессов.

Метод расчета с использованием аппарата теории марковских процессов

Пусть имеется некоторая система S. Говорят, что в сис­теме происходит случайный процесс, если она с течением вре­мени может под влиянием случайных факторов (например, отказов и восстановлений отдельных компонент) изменять свое состояние.

Система называется системой с дискретными состояниями, если она имеет счетное (в частном случае конечное) мно­жество возможных состояний S_o, S_u ... , S_h и переход из од­ного состояния в другое осуществляется скачком.

Для описания случайного процесса, протекающего в сис­теме с дискретными состояниями S_u, S_b ..., S*. пользуются ве-

роятностями состояний Po(t), Pi (t),... , Ph(t), где Pi{t), i— = (0, 1,... , k) —вероятность того, что система в момент вре­мени t находится в состоянии S,-. Вероятности Pi{t) удовлет­воряют условию



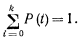
Случайный процесс в системе S называется процессом с дискретным временем, если переходы системы из одного сос­тояния в другое возможны только в определенные моменты

времени t_o,t\..... Если переходы возможны в любой момент

времени, то процесс называется процессом с непрерывным временем.

Случайный процесс с дискретными состояниями называет­ся марковским (или процессом без последействия), если все вероятностные характеристики процесса в будущем зависят лишь от того, в каком состоянии этот процесс находится в настоящий момент времени, и не зависит от того, каким об­разом этот процесс протекал в прошлом (будущее зависит от прошлого только через настоящее).

Марковский процесс представляет собой марковскую цепь с различными состояниями и может быть представлен матрицей значений переходных вероятностей



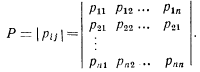
Элемент матрицы переходов рц соответствует вероятности того, что марковская цепь, находящаяся в состоянии S,-, на очередном шаге перейдет в состояние S/. Из самого опреде­ления марковской цепи ясно, что переходные вероятности не зависят от номера шага, т. е. процесс переходов стационар­ный во времени.

Таким образом, марковская цепь — дискретный случайный процесс с дискретным временем, у которого переходы осу­ществляются через некоторый интервал времени 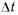из од­ного состояния в другое в счетном множестве состояний.

В марковском процессе длительность пребывания в каж­дом из состояний ^ Si величина случайная, имеющая свое рас­пределение 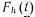для каждого k-го состояния. Причем все распределения F_k(t) подчиняются экспоненциальному закону.

Марковский процесс обладает характерными свойствами, определяемыми в первую очередь, эйспоненциальиостью рас­пределения времени пребывания процесса в каждом из сос­тояний:

стационарностью, когда переходные вероятности и длитель­ности пребывания в том или ином состоянии не зависят от то­го, в какой момент времени рассматривается этот процесс;

ординарностью,когда за бесконечно малый интервал време­ни не может произойти более одного перехода из одного со­стояния в другое состояние;

отсутствием последействия, когда вся последующая траек­тория перехода процесса из состояния а состояние зависит толь­ко от текущего состояния и не зависит от всей прошлой истории развития этого процесса или от любой его части.

Марковский процесс удобно описывать ориентированным графом переходов, вершины которого представляют собой состояния, а «веса» ребер соответствуют интенсивностям пе­рехода из одного состояния в другое. Понятно, что зная пе­реходные вероятности 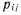и параметр 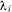распределения вре­мени пребывания процесса в данном i-м состоянии, можно легко найти эти «веса» по формуле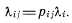



Если при описании процесса перехода системы из состоя­ния в состояние сохранить марковское свойство, можно счи­тать, что пребывание в каждом из состояний F_is(t) подчиня­ется произвольному (а не экспоненциальному) закону рас­пределения. Такой процесс называется полумарковским или неоднородным марковским.

В дальнейшем будем рассматривать только марковские процессы.

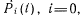
На основании графа переходов можно составить систему дифференциальных уравнений для нахождения вероятностей пребывания марковского процесса в состояниях 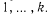. При этом следует руководствоваться следующим простым правилом. Производная (по /) от пребывания сис­темы в момент времени t в состоянии Pi{t) равна алгебраи­ческой сумме произведений интенсивности переходов на со­ответствующие вероятности. Слагаемым, которым соответст­вуют выходящие (из данного состояния) дуги графа, припи­сывается знак минус, остальным — плюс. Общее число сла­гаемых равно общему числу входящих и выходящих дуг.

Система дифференциальных уравнений содержит k диф­ференциальных уравнений и k неизвестных. Однако все эти уравнения линейно зависимы. Поэтому нужно дополнить их так называемым уравнением нормировки, которое показыва­ет, что сумма вероятностей событий, образующих полную группу, равна единице.

В результате одно любое из дифференциальных уравнений системы может быть исключено.

Различают два типа случайных процессов:

при первом же попадании в неработоспособное состояние процесс прекращается (процесс с поглощающим экраном);

система находится в стационарном режиме отказов и вос­становлений (процесс с отражающим экраном).

Первый процесс характерен для невосстанавливаемых из­делий, второй для восстанавливаемых.

Пример. Рассмотрим однокомпопентную восстанавливае­мую систему, имеющую два состояния: ^ Pi{t) —работоспо­собность; 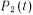—отказ; к — интенсивность отказа; µ — ин­тенсивность восстановления. Граф переходов этой системы (рис. 15). Запишем систему дифференциальных уравнений: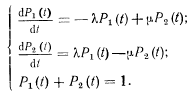



В предположении, что в момент t= 0 система работоспо­собна, т. е. 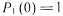, решение дифференциального уравнения имеет вид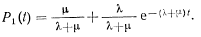



Выражение для 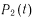легко находится из последнего урав­нения системы.

В стационарном режиме при 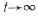значения производных равны нулю, а соответствующие начальные условия, естест­венно уже никакой роли не играют. В результате, вместо системы линейных дифференциальных получается система ли­нейных алгебраических уравнений. Изложенное справедливо только для систем с отражающим экраном.

Пример. Задана система дублирования с восстановлением (рис. 16). Граф переходов этой системы (рис. 17а).

Составляем систему дифференциальных уравнений:




При

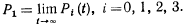
Тогда


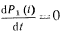
Следовательно,



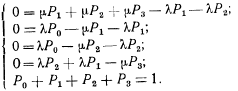
Решая систему уравнений, получаем



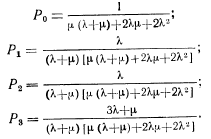
Из графа переходов системы следует, что



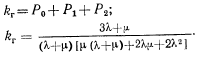
Для системы с поглощающим экраном, стационарного ре­жима не существует, с ростом времени вероятность для такой системы попасть в поглощающие состояния стремится к еди­нице.

Пример. Система дублирования без восстановления (с по­глощающим экраном). Граф переходов такой системы пред­ставлен «а рис. 17 6. Система дифференциальных уравнений имеет следующий вид:



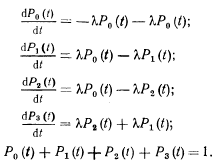
Начальные условия

.

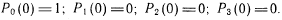В результате решения системы получаем



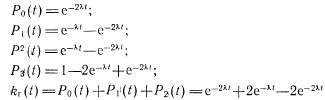
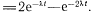
Если предположение об экспоненциальном законе распре­деления времени между событиями (отказами и восстановле­нием) не может быть принято, то используют для расчетов •надежности систем с восстановлением полумарковский про­цесс (обобщение марковского процесса).


^ 55. Методы приближенной оценки надежности цифровых устройств.


Достоверность работы цифровых устройств с тестовым диагностированием

Достоверность функционирования цифрового устройства, контроль которого осуществляется путем прохождения конт­рольного теста , будем определять за некоторый промежуток времени 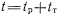, где 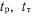— продолжительность основной работы и прохождения теста. Возможны два варианта реа­лизации тестового контроля (рис. 34):

включается основной рабочий режим (t_p);

выполняется контрольный тест .

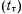Результат запоминается до окончания прохождения теста. Если тест не фиксирует наличие неисправности, дается раз­решение на дальнейшее использование этого результата. Во втором случае:

вначале проводится прогон теста (t_T);

затем реализуется рабочий режим '■(tp).

Выходной результат работы оценивается по результату тестирования.

Тест, составленный для проверки функционирования циф­рового устройства, по отношению ко всем возможным ошиб­кам обладает определенной обнаруживающей способностью. Обозначим ее Р_Обн_г. При этом предположим:

тестовым контролем устройство охвачено полностью;

отказы и сбои, происходящие в цифровом устройстве, вза­имно независимы, причем потоки отказов и сбоев являются простейшими.

Введем коэффициент избыточного времени k_B, который найдем как

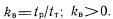(38)

Оценим достоверность функционирования цифрового уст­ройства для двух рассмотренных вариантов включения тес­та. Для сокращения в дальнейшем первый вариант включе­ния обозначим вариантом А, второй — вариантом Б.

Используя (5), (7) и (38), получим следующее.

Вариант А:



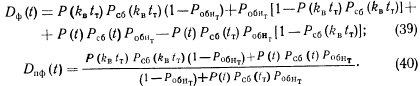
Если тест обеспечивает полную проверку 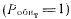, тогда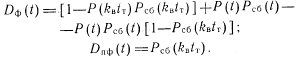



Если тестовый контроль отсутствует (Р_Обн_т=0), следова­тельно,



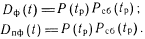
Вариант Б:





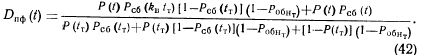
При Р_Обн_т = 1 имеем



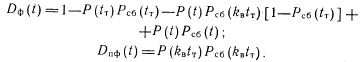
При Р_Обн_т = 0 получим



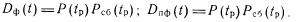
Из анализа (40) и (42) следует, что 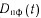для вариан­та А всегда больше, чем для варианта Б при любых значе­ниях k_B. Сравнение (39) и (41) показывает, что 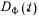при 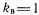для вариантов ^ А и Б одинакова; при k_B>l выше до­стоверность функционирования варианта A, при к_в<.1 — достоверность функционирования варианта Б.

Таким образом, организация тестирования по варианту ^ А позволяет получить более высокую достоверность работы. Однако использование тестового контроля по варианту А да­леко 'не всегда возможно (из-за необходимости задерживать выходную информацию, по крайней мере, на время 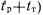. Поэтому остановимся на реализации тестового контроля по варианту Б.

Для повышения достоверности этого варианта, прежде всего, когда 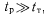, целесообразно ввести аппаратный конт­роль, который бы в период 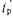в реальном масштабе времени определял истинное состояние цифрового устройства. Такой вид -контроля принято называть комбинированным.

Последовательность включения тестового и аппаратного контроля определяется временной диаграммой (рис. 34). В период t_T происходит обнаружение ошибок тестовым конт­ролем с вероятностью 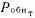, далее в период /_Р — обнаруже­ние ошибок аппаратным контролем с вероятностью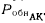

Информация, поступающая со средств аппаратного конт­роля в момент t_T, во внимание не принимается, т. е. досто­верность функционирования цифрового устройства в период t_т оценивается только по результату тестового контроля. Заме­тим, что вероятности обнаружения ошибок тестовым Р_Обн_т и аппаратным Р_оьа _АК контролем — события взаимно незави­симые.

Используя (5), (7), (13), (15) и (38) для комбинирован­ного ^контроля, можно получить расчетные формулы для по­казателе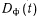й и 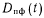. В общем виде эти формулы из-за громоздкости не приводятся. Для крайних случаев выраже­ния для 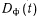и 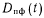имеют следующий вид:

тестовый и аппаратный контроль полный (т. е. Р_Обн_т =1,



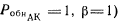
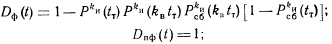
тестовый и аппаратный контроль отсутствует



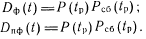
Встроенный аппаратный контроль повышает достовер­ность работы 'цифрового устройства, но одновременно приво­дит к снижению его безотказности вследствие увеличения объема оборудования.

Определим оптимальное значение вводимой аппаратурной избыточности, т. е. такого значения /г_и, при котором увели­чение выигрыша в достоверности еще не приводит к сущест­венному проигрышу в безотказности.

Зависимость 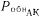от k_H для различных методов аппа­ратного контроля дана на рис. 35. По среднему и вспомога­тельному верхнему графикам строим зависимости 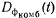, 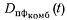от k_H (жирная сплошная для 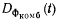и жирная штриховая для 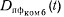(0 линии). Очевидно, что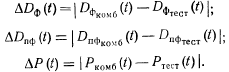



Тогда введение аппаратного контроля целесообразно, если 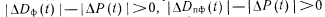(нижний гра­фик, рис. 35). Из этого графика следует, что имеет смысл ис­пользовать только такие методы аппаратного контроля, ко­торые требуют 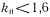, причем максимальный выигрыш в до­стоверности работы достигается при .

Рассмотрим достоверности функционирования и правиль­ного функционирования цифровых устройств с тестовым контролем для установившегося режима работы. Цифровое устройство может в общем случае находиться в трех сос­тояниях:

нерабочий режим (ожидание или пауза) —устройство может быть выключено либо включено, однако никакие ра­бочие сигналы на него не подаются и не снимаются;

дежурный режим — аппаратура включена и проводится прогон контрольного теста;

режим основной работы.

Обозначим длительности режимов ожидания, дежурного и основной работы соответственно 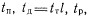, где t_т — вре­мя 'прохождения теста; l>0—целое положительное число.

Временная диаграмма работы цифровых устройств дана на рис. 36.

Переход из режима ожидания в дежурный и из дежурно­го режима в основной, а также окончание основного режима происходят в произвольный момент времени в зависимости от конкретной реальной обстановки. Отсюда следует, что ве­личины отрезков времен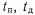и и 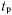распределены по случай­ному закону.

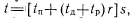, где г и s целые положительные числа 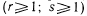. Обозначим 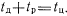. Примем, что нача­ло отсчета времени t совпадает с моментом окончания послед­них регламентных или профилактических работ, которые обеспечивают полное восстановление работоспособности циф­рового устройства.

Будем оценивать работу цифрового устройства по времен­ным отрезкам 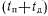и . Граф, описывающий работу устройства по этим отрезкам в соответствии с временной диа­граммой (рис. 36) и принятую стратегию обслуживания, представлен на рис. 37 а. На графе состояние Po(t) —состоя­ние работоспособности на отрезке времени 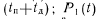— состояние отказа на отрезке времени 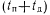, который может быть обнаружен тестовым контролем; 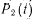—состояние от­каза на отрезке времени 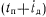, который не может быть обнаружен тестовым контролем; 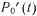—состояние работо­способности на отрезке времени 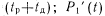—состояние отказа на отрезке времени 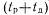, который может быть об­наружен тестовым контролем; 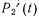—состояние отказа на отрезке времени 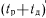, который не обнаруживается тесто­вым контролем; 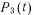—состояние отказа обнаруживаемого нетестовыми методами контроля в период проведения регла­ментных работ.

Если при тестовом контроле обнаружен отказ, то устрой­ство немедленно переходит в режим восстановления. На гра­фе 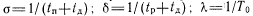—интенсивность от­казов; 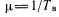— интенсивность восстановления; 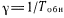— интенсивность обнаружения отказов нетестовыми методами контроля, причем

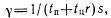(43)

где s — число полных циклов (циклов, включающих кроме отрезков времени t_п и t_д, время ожидания t_п) до проведения очередных регламентных работ.

При числе циклов г=1 вид графа упростится за счет ис­ключения петель в состояниях P₁'{t). и P₂'{t). Переходы с интенсивностью 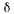из состояний P₁'{t). и P₂'{t) в состояния Р₀(t) и Р₂(t) соответственно происходят только через г циклов. До достижения г циклов переходы с интенсивностью 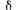из состояния P₁'{t). и P₂'{t) осуществляются в те же сос­тояния.

Для учета частоты переходов из состояний P₁'{t). и P₂'{t) в состояния Р₀(t) и Р₂(t) соответственно введем коэффи­циент



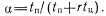
Предположим, как и в предыдущем параграфе, что пото­ки отказов, обнаружения (нетестовыми методами контроля) и восстановления — простейшие, а закон распределения вре­менных отрезков 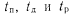экспоненциальный. Тогда можно утверждать, что процесс, описываемый графом (см. рис. 37 а), —марковский.

Составляя по графу систему дифференциальных уравне­ний (из-за громоздкости система уравнений не приводится), и, решая ее для стационарного режима работы аппаратуры, получим



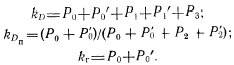
Развернутые выражения для расчета 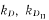и k_r из-за громоздкости не приводятся, они даны в [8]. По этим фор­мулам и с учетом (43) можно найти значение предельного числа полных циклов s, по истечению которых необходимо проводить регламентные работы.

Граф цифрового устройства с тестовым контролем по периодам времени /„, г_л и /_р ^представлен на рис. 37 6, где 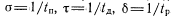, из которого следует: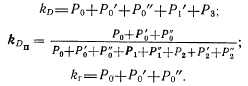



Для цифрового устройства с комбинированным контролем граф состояний будет иметь вид, приведенный на рис. 38. При этом полагается, что в режиме тестового контроля 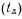информация, получаемая от средств аппаратного контроля, во внимание не принимается.

Из графа на рис. 38 запишем



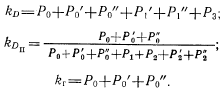
Если решить системы дифференциальных уравнений отно­сительно состояний цифрового устройства для графов на рис. 37 6 и рис. 38 и принять во внимание, что показатели k_D, k_Dn и k_T для цифрового устройства с комбинированным контро­лем должны быть выше соответствующих показателей для цифрового устройства с тестовым контролем, то можно найти предельное допустимое значение 'коэффициента избыточного оборудования 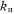, при котором введение аппаратного контро­ля целесообразно.